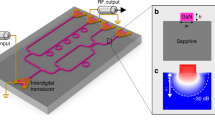
Abstract
Gauge fields in condensed matter physics give rise to nonreciprocal and topological transport phenomena and exotic electronic states1. Nanomechanical systems are applied as sensors and in signal processing, and feature strong nonlinearities. Gauge potentials acting on such systems could induce quantum Hall physics for phonons at the nanoscale. Here, we demonstrate a magnetic gauge field for nanomechanical vibrations in a scalable, on-chip optomechanical system. We induce the gauge field through multi-mode optomechanical interactions, which have been proposed as a resource for the necessary breaking of time-reversal symmetry2,3,4. In a dynamically modulated nanophotonic system, we observe how radiation pressure forces mediate phonon transport between resonators of different frequencies. The resulting controllable interaction, which is characterized by a high rate and nonreciprocal phase, mimics the Aharonov–Bohm effect5. We show that the introduced scheme does not require high-quality cavities, such that it allows exploring topological acoustic phases in many-mode systems resilient to realistic disorder.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the open-access repository Zenodo, with assigned digital object identifier (DOI) 10.5281/zenodo.3554024.
Code availability
The computer codes that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
Change history
07 April 2022
In the version of this article initially published, a conversion error led to “>” symbols appearing as “gt”, once in the paragraph above Eq. (2a) and twice in the paragraph below Eq. (3). The errors have been corrected in the HTML and PDF versions of the article.
References
Laughlin, R. B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 23, 5632 (1981).
Peano, V., Brendel, C., Schmidt, M. & Marquardt, F. Topological phases of sound and light. Phys. Rev. X 5, 031011 (2015).
Ruesink, F., Miri, M.-A., Alù, A. & Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 7, 13662 (2016).
Fang, K. et al. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 13, 465–471 (2017).
Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Goldman, N., Budich, J. & Zoller, P. Topological quantum matter with ultracold gases in optical lattices. Nat. Phys. 12, 639–645 (2016).
Huber, S. D. Topological mechanics. Nat. Phys. 12, 621–623 (2016).
Lindner, N. H., Refael, G. & Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 7, 490–495 (2011).
Dalibard, J., Gerbier, F., Juzeliuūnas, G. & Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011).
Bermudez, A., Schaetz, T. & Porras, D. Synthetic gauge fields for vibrational excitations of trapped ions. Phys. Rev. Lett. 107, 150501 (2011).
Fang, K., Yu, Z. & Fan, S. Photonic Aharonov–Bohm effect based on dynamic modulation. Phys. Rev. Lett. 108, 153901 (2012).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).
Nash, L. M. et al. Topological mechanics of gyroscopic metamaterials. Proc. Natl Acad. Sci. USA 112, 14495–14500 (2015).
Wang, Y. et al. Observation of nonreciprocal wave propagation in a dynamic phononic lattice. Phys. Rev. Lett. 121, 194301 (2018).
Cha, J., Kim, K. W. & Daraio, C. Experimental realization of on-chip topological nanoelectromechanical metamaterials. Nature 564, 229–233 (2018).
Shen, Z. et al. Experimental realization of optomechanically induced non-reciprocity. Nat. Photon. 10, 657–661 (2016).
Peterson, G. A. et al. Demonstration of efficient nonreciprocity in a microwave optomechanical circuit. Phys. Rev. X 7, 031001 (2017).
Bernier, N. R. et al. Nonreciprocal reconfigurable microwave optomechanical circuit. Nat. Commun. 8, 604 (2017).
Xu, H., Mason, D., Jiang, L. & Harris, J. Topological energy transfer in an optomechanical system with exceptional points. Nature 537, 80–83 (2016).
Xu, H., Jiang, L., Clerk, A. A. & Harris, J. G. E. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature 568, 65–69 (2019).
Walter, S. & Marquardt, F. Classical dynamical gauge fields in optomechanics. New J. Phys. 18, 113029 (2016).
Shkarin, A. et al. Optically mediated hybridization between two mechanical modes. Phys. Rev. Lett. 112, 013602 (2014).
Weaver, M. J. et al. Coherent optomechanical state transfer between disparate mechanical resonators. Nat. Commun. 8, 824 (2017).
Ockeloen-Korppi, C. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478–482 (2018).
Leijssen, R., La Gala, G. R., Freisem, L., Muhonen, J. T. & Verhagen, E. Nonlinear cavity optomechanics with nanomechanical thermal fluctuations. Nat. Commun. 8, 16024 (2017).
Okamoto, H. et al. Coherent phonon manipulation in coupled mechanical resonators. Nat. Phys. 9, 480–484 (2013).
Faust, T., Rieger, J., Seitner, M. J., Kotthaus, J. P. & Weig, E. M. Coherent control of a classical nanomechanical two-level system. Nat. Phys. 9, 485–488 (2013).
Tzuang, L. D., Fang, K., Nussenzveig, P., Fan, S. & Lipson, M. Non-reciprocal phase shift induced by an effective magnetic flux for light. Nat. Photon. 8, 701–705 (2014).
Roushan, P. et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 13, 146–151 (2017).
Celi, A. et al. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett. 112, 043001 (2014).
Hatanaka, D., Mahboob, I., Onomitsu, K. & Yamaguchi, H. Phonon waveguides for electromechanical circuits. Nat. Nanotechnol. 9, 520–524 (2014).
Cha, J. & Daraio, C. Electrical tuning of elastic wave propagation in nanomechanical lattices at MHz frequencies. Nat. Nanotechnol. 13, 1016–1020 (2018).
Groth, C. W., Wimmer, M., Akhmerov, A. R. & Waintal, X. Kwant: a software package for quantum transport. New J. Phys. 16, 063065 (2014).
Acknowledgements
This work is part of the research programme of the Netherlands Organisation for Scientific Research (NWO). The authors acknowledge support from the Office of Naval Research (grant no. N00014-16-1-2466), the European Research Council (ERC starting grant no. 759644-TOPP) and the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 732894 (FET Proactive HOT).
Author information
Authors and Affiliations
Contributions
J.P.M. performed the experiments and analysed the data. J.d.P. developed the theoretical model. E.V. supervised the project. All authors contributed to the interpretation of results and writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
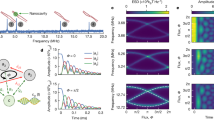
Extended Data Fig. 1 Detuning dependent phonon transfer.
a,b,c, Mode transfer measurements for a detuning of \(\Delta /k\ \simeq\) 0.25, 0.01, and \(-0.23\) respectively. The left two panels show the driven response of mode 1 and simultaneously measured transferred response to mode 2 for a fixed \({\omega }_{{\rm{m}}}\) chosen at each detuning. The phase imprint on mode 2 as a function of the modulation phase is shown in the rightmost panels. There is no clear phase pickup for near-zero detuning of the drive laser. The dashed line in the transferred response corresponds to the average magnitude of the transfer signal measured during the phase transfer measurement.
Extended Data Fig. 2 Robust phononic edge states.
a, Optical spring shift measured at higher optical powers for a separate device shows large tunability of the mechanical modes. The dashed, white line shows the drive laser detuning used in b. The unusual features between 193.0 and 193.2 THz are due to a dynamically unstable regime of potential photothermoelastic origin. b, The modulated coupling strength, geff, is higher for higher optical powers. The largest modulated coupling strength measured in our experiments is marked by the dashed line and seen to be \(\sim 2\pi \times 200\) kHz. Here the detection laser was absent and the drive laser response was directly demodulated using the lock-in amplifier leading to a Fano shaped feature for the driven response. c,d,e, (top panels) Band structure for a ribbon geometry (width \(L=20\)) for increasing values of the direct mechanical coupling from left to right (0, 10, and 20 kHz, respectively), displaying the driving modulation frequency. The steady-state phononic amplitude in the absence of disorder is displayed in the middle row, while the result with a phononic frequency disorder with standard deviation \({\sigma }_{\Omega }/2\pi\) = 20 kHz (averaged over 100 realizations) is shown at the bottom. For these plots, \(p/q=1/3\).
Supplementary information
Supplementary Information
Supplementary equations, Figs. 1–4 and refs. 1–16.
Rights and permissions
About this article
Cite this article
Mathew, J.P., Pino, J.d. & Verhagen, E. Synthetic gauge fields for phonon transport in a nano-optomechanical system. Nat. Nanotechnol. 15, 198–202 (2020). https://doi.org/10.1038/s41565-019-0630-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-019-0630-8
This article is cited by
-
Optomechanical realization of the bosonic Kitaev chain
Nature (2024)
-
Non-reciprocal topological solitons in active metamaterials
Nature (2024)
-
Quadrature nonreciprocity in bosonic networks without breaking time-reversal symmetry
Nature Physics (2023)
-
Asynchronous locking in metamaterials of fluids of light and sound
Nature Communications (2023)
-
Phase-controlled quantum optomechanics
Science China Physics, Mechanics & Astronomy (2023)