Abstract
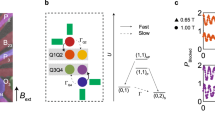
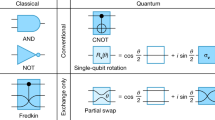
Quantum computation requires qubits that satisfy often-conflicting criteria, which include long-lasting coherence and scalable control1. One approach to creating a suitable qubit is to operate in an encoded subspace of several physical qubits. Although such encoded qubits may be particularly susceptible to leakage out of their computational subspace, they can be insensitive to certain noise processes2,3 and can also allow logical control with a single type of entangling interaction4 while maintaining favourable features of the underlying physical system. Here we demonstrate high-fidelity operation of an exchange-only qubit encoded in a subsystem of three coupled electron spins5 confined in gated, isotopically enhanced silicon quantum dots6. This encoding requires neither high-frequency electric nor magnetic fields for control, and instead relies exclusively on the exchange interaction4,5, which is highly local and can be modulated with a large on–off ratio using only fast voltage pulses. It is also compatible with very low and gradient-free magnetic field environments, which simplifies integration with superconducting materials. We developed and employed a modified blind randomized benchmarking protocol that determines both computational and leakage errors7,8, and found that unitary operations have an average total error of 0.35%, with half of that, 0.17%, coming from leakage driven by interactions with substrate nuclear spins. The combination of this proven performance with complete control via gate voltages makes the exchange-only qubit especially attractive for use in many-qubit systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper are available from the corresponding author upon reasonable request.
References
Ladd, T. D. et al. Quantum computers. Nature 464, 45 (2010).
Zanardi, P. & Rasetti, M. Noiseless quantum codes. Phys. Rev. Lett. 79, 3306–3309 (1997).
Lidar, D. A., Chuang, I. L. & Whaley, K. B. Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 81, 2594–2597 (1998).
DiVincenzo, D. P., Bacon, D., Kempe, J., Burkard, G. & Whaley, K. B. Universal quantum computation with the exchange interaction. Nature 408, 339–342 (2000).
Medford, J. et al. Self-consistent measurement and state tomography of an exchange-only spin qubit. Nat. Nanotechnol. 8, 654–659 (2013).
Eng, K. et al. Isotopically enhanced triple-quantum-dot qubit. Sci. Adv. 1, e1500214 (2015).
Wallman, J. J., Barnhill, M. & Emerson, J. Robust characterization of leakage errors. New J. Phys. 18, 043021 (2016).
Wood, C. J. & Gambetta, J. M. Quantification and characterization of leakage errors. Phys. Rev. A 97, 032306 (2018).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Kawakami, E. et al. Gate fidelity and coherence of an electron spin in an Si/SiGe quantum dot with micromagnet. Proc. Natl Acad. Sci. USA 113, 11738–11743 (2016).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).
Russ, M. & Burkard, G. Three-electron spin qubits. J. Phys. Condens. Matter 29, 393001 (2017).
Levy, J. Universal quantum computation with spin-1/2 pairs and Heisenberg exchange. Phys. Rev. Lett. 89, 147902 (2002).
Jones, A. M. et al. Spin-blockade spectroscopy of Si/SiGe quantum dots. Preprint at http://arxiv.org/abs/1809.08320 (2018).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Ladd, T. D. Hyperfine-induced decay in triple quantum dots. Phys. Rev. B 86, 125408 (2012).
Reed, M. D. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).
Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).
Lowenthal, F. Uniform finite generation of the rotation group. Rocky Mt. J. Math. 1, 575–586 (1971).
Fong, B. H. & Wandzura, S. M. Universal quantum computation and leakage reduction in the 3-qubit decoherence free subsystem. Quantum Inf. Comput. 11, 1003–1018 (2011).
Emerson, J. et al. Symmetrized characterization of noisy quantum processes. Science 317, 1893–1896 (2007).
Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A 77, 012307 (2008).
Helson, J., Wallman, J. J., Flammia, S. T. & Wehner, S. Multi-qubit randomized benchmarking using few samples. Preprint at http://arxiv.org/abs/1701.04299v2 (2018).
Xue, X. et al. Benchmarking gate fidelities in a Si/SiGe two-qubit device. Phys. Rev. X 9, 021011 (2019).
Hickman, G. T., Wang, X., Kestner, J. P. & Das Sarma, S. Dynamically corrected gates for an exchange-only qubit. Phys. Rev. B 88, 161303 (2013).
Cerfontaine, P. et al. Closed-loop control of a GaAs-based singlet-triplet spin qubit with 99.5% gate fidelity and low leakage. Preprint at http://arxiv.org/abs/1906.06169 (2019).
Johnson, B. R. et al. Quantum non-demolition detection of single microwave photons in a circuit. Nat. Phys. 6, 663–667 (2010).
Borselli, M. G. et al. Undoped accumulation-mode Si/SiGe quantum dots. Nanotechnology 26, 375202 (2015).
Zajac, D. M., Hazard, T. M., Mi, X., Wang, K. & Petta, J. R. A reconfigurable gate architecture for Si/SiGe quantum dots. Appl. Phys. Lett. 106, 223507 (2015).
Acknowledgements
We thank A. Hunter, K. Eng, M. Gyure and B. Fong for valuable contributions that led to this work.
Author information
Authors and Affiliations
Contributions
The device was designed, characterized and fabricated by S.D.H., M.P.J., M.L., M.T.R. and M.G.B. Control theory, coding and analysis were provided by C.J., A.M.J., S.M., S.T.M., A.S., A.J.W. and T.D.L. Measurements were made by R.W.A., M.D.R., A.M.J., J.K., S.M., B.S. and A.J.W. The manuscript was written by R.W.A., C.J., M.D.R., A.M.J. and T.D.L. with input from all the authors. The effort was supervised by M.T.R., T.D.L. and M.G.B.
Corresponding author
Ethics declarations
Competiting interests
The authors declare no competiting interests.
Additional information
Peer review information: Nature Nanotechnology thanks David DiVincenzo, Veit Langrock and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–3 and Supplementary Table 1.
Rights and permissions
About this article
Cite this article
Andrews, R.W., Jones, C., Reed, M.D. et al. Quantifying error and leakage in an encoded Si/SiGe triple-dot qubit. Nat. Nanotechnol. 14, 747–750 (2019). https://doi.org/10.1038/s41565-019-0500-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-019-0500-4
This article is cited by
-
Simultaneous single-qubit driving of semiconductor spin qubits at the fault-tolerant threshold
Nature Communications (2023)
-
Coherent spin–valley oscillations in silicon
Nature Physics (2023)
-
Universal logic with encoded spin qubits in silicon
Nature (2023)
-
Review of performance metrics of spin qubits in gated semiconducting nanostructures
Nature Reviews Physics (2022)
-
Qubits made by advanced semiconductor manufacturing
Nature Electronics (2022)