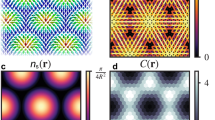
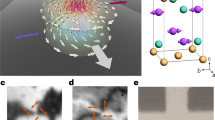
Abstract
Geometric frustration emerges when local interaction energies in an ordered lattice structure cannot be simultaneously minimized, resulting in a large number of degenerate states. The numerous degenerate configurations may lead to practical applications in microelectronics1, such as data storage, memory and logic2. However, it is difficult to achieve very high degeneracy, especially in a two-dimensional system3,4. Here, we showcase in situ controllable geometric frustration with high degeneracy in a two-dimensional flux-quantum system. We create this in a superconducting thin film placed underneath a reconfigurable artificial-spin-ice structure5. The tunable magnetic charges in the artificial-spin-ice strongly interact with the flux quanta in the superconductor, enabling switching between frustrated and crystallized flux quanta states. The different states have measurable effects on the superconducting critical current profile, which can be reconfigured by precise selection of the spin-ice magnetic state through the application of an external magnetic field. We demonstrate the applicability of these effects by realizing a reprogrammable flux quanta diode. The tailoring of the energy landscape of interacting ‘particles’ using artificial-spin-ices provides a new paradigm for the design of geometric frustration, which could illuminate a path to control new functionalities in other material systems, such as magnetic skyrmions6, electrons and holes in two-dimensional materials7,8, and topological insulators9, as well as colloids in soft materials10,11,12,13.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Ramirez, A. P. Geometric frustration: magic moments. Nature 421, 483 (2003).
Heyderman, L. J. & Stamps, R. L. Artificial ferroic systems: novel functionality from structure, interactions and dynamics. J. Phys. Condens. Matter 25, 363201 (2013).
Perrin, Y., Canals, B. & Rougemaille, N. Extensive degeneracy, Coulomb phase and magnetic monopoles in artificial square ice. Nature 540, 410–413 (2016).
Lieb, E. H. Residual entropy of square ice. Phys. Rev. 162, 162–172 (1967).
Wang, Y.-L. et al. Rewritable artificial magnetic charge ice. Science 352, 962–966 (2016).
Ma, F., Reichhardt, C., Gan, W., Reichhardt, C. J. O. & Lew, W. S. Emergent geometric frustration of artificial magnetic skyrmion crystals. Phys. Rev. B 94, 144405 (2016).
Singha, A. et al. Two-dimensional Mott–Hubbard electrons in an artificial honeycomb lattice. Science 332, 1176–1179 (2011).
Taillefumier, M., Dugaev, V. K., Canals, B., Lacroix, C. & Bruno, P. Graphene in a periodically alternating magnetic field: an unusual quantization of the anomalous Hall effect. Phys. Rev. B 84, 085427 (2011).
Gilbert, I., Nisoli, C. & Schiffer, P. Frustration by design. Phys. Today 69, 54–59 (2016).
Loehr, J., Ortiz-Ambriz, A. & Tierno, P. Defect dynamics in artificial colloidal ice: real-time observation, manipulation, and logic gate. Phys. Rev. Lett. 117, 168001 (2016).
Ortiz-Ambriz, A. & Tierno, P. Engineering of frustration in colloidal artificial ices realized on microfeatured grooved lattices. Nat. Commun. 7, 10575 (2016).
Han, Y. et al. Geometric frustration in buckled colloidal monolayers. Nature 456, 898–903 (2008).
Libal, A., Reichhardt, C. & Olson, C. J. Realizing colloidal artificial ice on arrays of optical traps. Phys. Rev. Lett. 97, 228302 (2006).
Gammel, P. Why vortices matter. Nature 411, 434–435 (2001).
Savel’ev, S. & Nori, F. Experimentally realizable devices for controlling the motion of magnetic flux quanta in anisotropic superconductors. Nat. Mater. 1, 179–184 (2002).
Park, K. & Huse, D. A. Superconducting phase with fractional vortices in the frustrated kagome wire network at f = 1/2. Phys. Rev. B 64, 134522 (2001).
Libal, A., Olson, C. J. & Reichhardt, C. Creating artificial ice states using vortices in nanostructured superconductors. Phys. Rev. Lett. 102, 237004 (2009).
Latimer, M. L., Berdiyorov, G. R., Xiao, Z. L., Peeters, F. M. & Kwok, W. K. Realization of artificial ice systems for magnetic vortices in a superconducting MoGe thin film with patterned nanostructures. Phys. Rev. Lett. 111, 067001 (2013).
Trastoy, J. et al. Freezing and thawing of artificial ice by thermal switching of geometric frustration in magnetic flux lattices. Nat. Nanotech. 9, 710–715 (2014).
Nisoli, C., Moessner, R. & Schiffer, P. Colloquium: artificial spin ice: designing and imaging magnetic frustration. Rev. Mod. Phys. 85, 1473–1490 (2013).
Wang, R. F. et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).
Nisoli, C. et al. Effective temperature in an interacting vertex system: theory and experiment on artificial spin ice. Phys. Rev. Lett. 105, 047205 (2010).
Farhan, A. et al. Direct observation of thermal relaxation in artificial spin ice. Phys. Rev. Lett. 111, 057204 (2013).
Zhang, S. et al. Crystallites of magnetic charges in artificial spin ice. Nature 500, 553–557 (2013).
Morgan, J. P., Stein, A., Langridge, S. & Marrows, C. H.Thermal ground-state ordering and elementary excitations in artificial magnetic square ice. Nat. Phys. 7, 75–79 (2011).
Kapaklis, V. et al. Thermal fluctuations in artificial spin ice. Nat. Nanotech. 9, 514–519 (2014).
Moller, G. & Moessner, R. Artificial square ice and related dipolar nanoarrays. Phys. Rev. Lett. 96, 237202 (2006).
Nisoli, C. Dumping topological charges on neighbors: ice manifolds for colloids and vortices. New J. Phys. 16, 113049 (2014).
Nisoli, C. Spin ice vs. thin ice. Preprint at https://arxiv.org/abs/1802.07900 (2018).
Milosevic, M. V. & Peeters, F. M. Vortex pinning in a superconducting film due to in-plane magnetized ferromagnets of different shapes: the London approximation. Phys. Rev. B 69, 104522 (2004).
Baert, M., Metlushko, V. V., Jonckheere, R., Moshchalkov, V. V. & Bruynseraede, Y. Composite flux-line lattices stabilized in superconducting films by a regular array of artificial defects. Phys. Rev. Lett. 74, 3269–3272 (1995).
Mengotti, E. et al. Real-space observation of emergent magnetic monopoles and associated Dirac strings in artificial kagome spin ice. Nat. Phys. 7, 68–74 (2011).
Villegas, J. E. et al. A superconducting reversible rectifier that controls the motion of magnetic flux quanta. Science 302, 1188–1191 (2003).
De Souza Silva, C. C., de Vondel, J. V., Morelle, M. & Moshchalkov, V. V. Controlled multiple reversals of a ratchet effect. Nature 440, 651–654 (2006).
Lee, C. S., Janko, B., Derenyi, I. & Barabasi, A. L. Reducing vortex density in superconductors using the ‘ratchet effect’. Nature 400, 337–340 (1999).
De Souza Silva, C. C. et al. Dipole-induced vortex ratchets in superconducting films with arrays of micromagnets. Phys. Rev. Lett. 98, 117005 (2007).
Wang, Y. L. et al. Parallel magnetic field suppresses dissipation in superconducting nanostripes. Proc. Natl Acad. Sci. USA 114, E10274 (2017).
Sadovskyy, A., Wang, Y. L., Xiao, Z.-L., Kwok, W.-K. & Glatz, A. Effect of hexagonal patterned arrays and defect geometry on the critical current of superconducting films. Phys. Rev. B 95, 075303 (2017).
Wang, Y. L. et al. Enhancing superconducting critical current by randomness. Phys. Rev. B 93, 045111 (2016).
Wang, Y. L. et al. Enhancing the critical current of a superconducting film in a wide range of magnetic fields with a conformal array of nanoscale holes. Phys. Rev. B 87, 220501 (2013).
White, W. R., Kapitulnik, A. & Beasley, M. R. Collective vortex motion in a-MoGe superconducting thin films. Phys. Rev. Lett. 70, 670–673 (1993).
Reichhardt, C., Ray, D. & Reichhardt, C. J. O. Reversible ratchet effects for vortices in conformal pinning arrays. Phys. Rev. B 91, 184502 (2015).
Reichhardt, C. & Gronbech-Jensen, N. Critical currents and vortex states at fractional matching fields in superconductors with periodic pinning. Phys. Rev. B 63, 054510 (2001).
Acknowledgements
This work was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. Use of the Center for Nanoscale Materials, an Office of Science user facility, was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract number DE-AC02-06CH11357. Z.-L.X. and J.X. acknowledge National Science Foundation grant DMR-1407175.
Author information
Authors and Affiliations
Contributions
Y.-L.W., Z.-L.X., B.J. and W.-K.K. conceived and supervised the project. Y.-L.W., J.X., Z.-L.X. and W.-K.K. designed the experiments. X.M. and B.J. designed the simulations. Y.-L.W., J.X., R.D., L.E.O. and J.E.P. fabricated samples. Y.-L.W., J.X. and A.S. conducted the measurements. X.M. conducted the simulations. Y.-L.W., X.M. and J.X., analysed the data. Y.-L.W., X.M., J.X., Z.-L.X., B.J. and W.-K.K. co-wrote the manuscript. All authors contributed to the discussion of the data and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–10, Supplementary Video Captions
Supplementary Video 1
d.c. transport property under type-II MC configuration at B/BΦ = 1.5
Supplementary Video 2
d.c. transport property under type-II MC configuration at B/BΦ = 0.5
Supplementary Video 3
d.c. transport property under type-II MC configuration at B/BΦ = 1.0
Rights and permissions
About this article
Cite this article
Wang, YL., Ma, X., Xu, J. et al. Switchable geometric frustration in an artificial-spin-ice–superconductor heterosystem. Nature Nanotech 13, 560–565 (2018). https://doi.org/10.1038/s41565-018-0162-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-018-0162-7
This article is cited by
-
Toroidic phase transitions in a direct-kagome artificial spin ice
Nature Nanotechnology (2024)
-
Kagome qubit ice
Nature Communications (2023)
-
Geometrical control of topological charge transfer in Shakti-Cairo colloidal ice
Communications Physics (2023)
-
Distinguishing artificial spin ice states using magnetoresistance effect for neuromorphic computing
Nature Communications (2023)
-
Tunable Magnetic Labyrinth for Abrikosov Vortices
Journal of Superconductivity and Novel Magnetism (2022)