Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Band structure engineering of 2D materials using patterned dielectric superlattices

Nature Nanotechnology volume 13, pages 566–571 (2018)Cite this article

Subjects

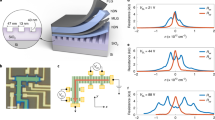
Abstract

The ability to manipulate electrons in two-dimensional materials with external electric fields provides a route to synthetic band engineering. By imposing artificially designed and spatially periodic superlattice potentials, electronic properties can be further altered beyond the constraints of naturally occurring atomic crystals1,2,3,4,5. Here, we report a new approach to fabricate high-mobility superlattice devices by integrating surface dielectric patterning with atomically thin van der Waals materials. By separating the device assembly and superlattice fabrication processes, we address the intractable trade-off between device processing and mobility degradation that constrains superlattice engineering in conventional systems. The improved electrostatics of atomically thin materials allows smaller wavelength superlattice patterns relative to previous demonstrations. Moreover, we observe the formation of replica Dirac cones in ballistic graphene devices with sub-40 nm wavelength superlattices and report fractal Hofstadter spectra6,7,8 under large magnetic fields from superlattices with designed lattice symmetries that differ from that of the host crystal. Our results establish a robust and versatile technique for band structure engineering of graphene and related van der Waals materials with dynamic tunability.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Patterned dielectric superlattice design.
Fig. 2: Transport measurements and band structure of a triangular SL device.
Fig. 3: Fractal Hofstadter spectrum under magnetic field.
Fig. 4: Magnetic subband structure in triangular and square SL systems.

References

  1. Esaki, L. & Tsu, R. Superlattice and negative differential conductivity in semiconductors. IBM J. Res. Dev. 14, 61–65 (1970).

    Article  Google Scholar 

  2. Ismail, K., Chu, W., Yen, A., Antoniadis, D. A. & Smith, H. I. Negative transconductance and negative differential resistance in a grid-gate modulation-doped field-effect transistor. Appl. Phys. Lett. 54, 460–462 (1989).

    Article  Google Scholar 

  3. Weiss, D., Klitzing, K. V., Ploog, K. & Weimann, G. Magnetoresistance oscillations in a two-dimensional electron gas induced by a submicrometer periodic potential. Europhys. Lett. 8, 179–184 (1989).

    Article  Google Scholar 

  4. Schlösser, T., Ensslin, K., Kotthaus, J. P. & Holland, M. Landau subbands generated by a lateral electrostatic superlattice—chasing the Hofstadter butterfly. Semicond. Sci. Technol. 11, 1582–1585 (1996).

    Article  Google Scholar 

  5. Albrecht, C. et al. Evidence of Hofstadter’s fractal energy spectrum in the quantized Hall conductance. Phys. Rev. Lett. 86, 147–150 (2001).

    Article  Google Scholar 

  6. Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).

    Article  Google Scholar 

  7. Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).

    Article  Google Scholar 

  8. Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).

    Article  Google Scholar 

  9. Hua Wang, Q., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotech. 7, 699–712 (2012).

    Article  Google Scholar 

  10. Park, C.-H., Yang, L., Son, Y.-W., Cohen, M. L. & Louie, S. G. Anisotropic behaviours of massless Dirac fermions in graphene under periodic potentials. Nat. Phys. 4, 213–217 (2008).

    Article  Google Scholar 

  11. Park, C. H., Son, Y. W., Yang, L., Cohen, M. L. & Louie, S. G. Electron beam supercollimation in graphene superlattices. Nano Lett. 8, 2920–2924 (2008).

    Article  Google Scholar 

  12. Barbier, M., Vasilopoulos, P. & Peeters, F. M. Extra Dirac points in the energy spectrum for superlattices on single-layer graphene. Phys. Rev. B 81, 75438 (2010).

    Article  Google Scholar 

  13. Dubey, S. et al. Tunable superlattice in graphene to control the number of Dirac points. Nano Lett. 13, 3990–3995 (2013).

    Article  Google Scholar 

  14. Drienovsky, M. et al. Towards superlattices: lateral bipolar multibarriers in graphene. Phys. Rev. B 89, 115421 (2014).

    Article  Google Scholar 

  15. Drienovsky, M. et al. Few-layer graphene patterned bottom gates for van der Waals heterostructures. Preprint at https://arxiv.org/abs/1703.05631 (2017).

  16. Sun, Z. et al. Towards hybrid superlattices in graphene. Nat. Commun. 2, 559 (2011).

    Article  Google Scholar 

  17. Bai, J., Zhong, X., Jiang, S., Huang, Y. & Duan, X. Graphene nanomesh. Nat. Nanotech. 5, 190–194 (2010).

    Article  Google Scholar 

  18. Sandner, A. et al. Ballistic transport in graphene antidot lattices. Nano Lett. 15, 8402–8406 (2015).

    Article  Google Scholar 

  19. Yagi, R. et al. Ballistic transport in graphene antidot lattices. Phys. Rev. B 92, 195406 (2015).

    Article  Google Scholar 

  20. Zhang, Y., Kim, Y., Gilbert, M. J. & Mason, N. Electronic transport in a two-dimensional superlattice engineered via self-assembled nanostructures. Preprint at https://arxiv.org/abs/1703.05689 (2017).

  21. Yankowitz, M., Xue, J. & LeRoy, B. J. Graphene on hexagonal boron nitride. J. Phys. Condens. Matter 26, 303201 (2014).

    Article  Google Scholar 

  22. Lee, M. et al. Ballistic miniband conduction in a graphene superlattice. Science 353, 1526–1529 (2016).

    Article  Google Scholar 

  23. Scarabelli, D. et al. Fabrication of artificial graphene in a GaAs quantum heterostructure. J. Vac. Sci. Technol. B 33, 06FG03 (2015).

    Article  Google Scholar 

  24. Lee, G.-H. et al. Electron tunneling through atomically flat and ultrathin hexagonal boron nitride. Appl. Phys. Lett. 99, 243114 (2011).

    Article  Google Scholar 

  25. Britnell, L. et al. Electron tunneling through ultrathin boron nitride crystalline barriers. Nano Lett. 12, 1707–1710 (2012).

    Article  Google Scholar 

  26. Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).

    Article  Google Scholar 

  27. Park, C. H., Yang, L., Son, Y. W., Cohen, M. L. & Louie, S. G. New generation of massless Dirac fermions in graphene under external periodic potentials. Phys. Rev. Lett. 101, 126804 (2008).

    Article  Google Scholar 

  28. Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).

    Article  Google Scholar 

  29. Langbein, D. The tight-binding and the nearly-free-electron approach to lattice electrons in external magnetic fields. Phys. Rev. 180, 633–648 (1969).

    Article  Google Scholar 

  30. Wannier, G. H. A result not dependent on rationality for Bloch electrons in a magnetic field. Phys. Status Solidi B Basic Solid State Phys. 88, 757–765 (1978).

    Article  Google Scholar 

  31. Claro, F. H. & Wannier, G. H. Magnetic subband structure of electrons in hexagonal lattices. Phys. Rev. B 19, 6068–6074 (1979).

    Article  Google Scholar 

  32. MacDonald, A. H. Landau-level subband structure of electrons on a square lattice. Phys. Rev. B 28, 6713–6717 (1983).

    Article  Google Scholar 

  33. Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2014).

    Article  Google Scholar 

Download references

Acknowledgements

Development of the device concept and fabrication process was supported by the Office of Naval Research (ONR) Young Investors Program (no. N00014-17-1-2832). Investigation of the fractal band structure under applied magnetic fields was supported by the National Science Foundation (DMR-1462383). C.F. was supported by National Science Foundation (NSF) Graduate Research Fellowship Program (DGE-14-44869) and the NSF Integrative Graduate Education and Research Training fellowship program (DGE-1069240). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement no. DMR-0654118, the State of Florida and the US Department of Energy. STM work is supported by the ONR (no. N00014-14-1-0501). P.M. acknowledges the support of New York University (NYU) Shanghai (Start-up Funds), NYU-ECNU (East China Normal University) Institute of Physics, and the NSF of China Research Fund for International Young Scientists (grant no. 11550110177). This research was carried out on the High Performance Computing resources at NYU Shanghai. M.K. was supported by JSPS (Japan Society for the Promotion of Science) KAKENHI (grant no. JP25107005, JP25107001 and JP15K21722). P.K. acknowledges support from ONR Multidisciplinary University Research Initiatives program on Quantum Optomechanics (grant no. N00014-15-1-2761).

Author information

Authors and Affiliations

  1. Department of Physics, Columbia University, New York, NY, USA

    Carlos Forsythe, Xiaodong Zhou, Abhay Pasupathy & Cory R. Dean

  2. Laboratory of Advanced Materials, Fudan University, Shanghai, China

    Xiaodong Zhou

  3. National Institute for Materials Science, Tsukuba, Japan

    Kenji Watanabe & Takashi Taniguchi

  4. NYU Shanghai, Shanghai, China

    Pilkyung Moon

  5. NYU-ECNU Institute of Physics at NYU Shanghai, Shanghai, China

    Pilkyung Moon

  6. Department of Physics, Osaka University, Toyonaka, Japan

    Mikito Koshino

  7. Department of Physics, Harvard University, Cambridge, MA, USA

    Philip Kim

Authors
  1. Carlos Forsythe
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaodong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kenji Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Takashi Taniguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Abhay Pasupathy
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Pilkyung Moon
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Mikito Koshino
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Philip Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Cory R. Dean
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

C.F., P.K. and C.R.D. conceived of the experiment. C.F. fabricated the samples, performed transport measurements and analysed transport data. P.M. and M.K. provided theoretical modelling of the system. X.Z. and A.P. performed STM measurements and analysed STM data. C.F., P.M., M.K., A.P., P.K. and C.R.D. co-wrote the paper. K.W. and T.T. provided hBN material for device fabrication.

Corresponding author

Correspondence to Cory R. Dean.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figures 1–14, Supplementary References

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Forsythe, C., Zhou, X., Watanabe, K. et al. Band structure engineering of 2D materials using patterned dielectric superlattices. Nature Nanotech 13, 566–571 (2018). https://doi.org/10.1038/s41565-018-0138-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41565-018-0138-7

This article is cited by

Search

Advanced search

Quick links

Find nanotechnology articles, nanomaterial data and patents all in one place. Visit Nano by Nature Research