Abstract
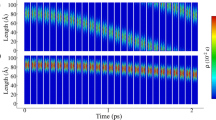
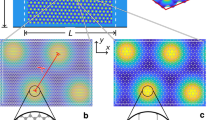
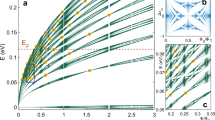
Charge carriers in graphene behave like massless Dirac fermions (MDFs) with linear energy-momentum dispersion1, 2, providing a condensed-matter platform for studying quasiparticles with relativistic-like features. Artificial graphene (AG)—a structure with an artificial honeycomb lattice—exhibits novel phenomena due to the tunable interplay between topology and quasiparticle interactions3,4,5,6. So far, the emergence of a Dirac band structure supporting MDFs has been observed in AG using molecular5, atomic6, 7 and photonic systems8,9,10, including those with semiconductor microcavities11. Here, we report the realization of an AG that has a band structure with vanishing density of states consistent with the presence of MDFs. This observation is enabled by a very small lattice constant (a = 50 nm) of the nanofabricated AG patterns superimposed on a two-dimensional electron gas hosted by a high-quality GaAs quantum well. Resonant inelastic light-scattering spectra reveal low-lying transitions that are not present in the unpatterned GaAs quantum well. These excitations reveal the energy dependence of the joint density of states for AG band transitions. Fermi level tuning through the Dirac point results in a collapse of the density of states at low transition energy, suggesting the emergence of the MDF linear dispersion in the AG.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Zhang, Y. B., Tan, Y. W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
Park, C. H. & Louie, S. G. Making massless Dirac fermions from a patterned two-dimensional electron gas. Nano Lett. 9, 1793–1797 (2009).
Gibertini, M. et al. Engineering artificial graphene in a two-dimensional electron gas. Phys. Rev. B 79, 241406 (2009).
Gomes, K. K., Mar, W., Ko, W., Guinea, F. & Manoharan, H. C. Designer Dirac fermions and topological phases in molecular graphene. Nature 483, 306–310 (2012).
Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. & Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012).
Graß, T., Chhajlany, R., Tarruell, L., Pellegrini, V. & Lewenstein, M. Proximity effects in cold atom artificial graphene. 2D Mater. 4, 015039 (2017).
Sepkhanov, R. A., Bazally, Ya. B. & Beenakker, C. W. Extremal transmission at the Dirac point of a photonic band structure. Phys. Rev. A 75, 063813 (2007).
Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).
Ling, L., Joannopoulos, J. D. & Soljacic, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Jacqmin, T. et al. Direct observation of Dirac cones and a flatband in a honeycomb lattice for polaritons. Phys. Rev. Lett. 112, 116402 (2014).
Heitmann, D. & Kotthaus, J. The spectroscopy of quantum dot arrays. Phys. Today 46, 56–63 (1993).
Hirler, F. et al. Spatially direct and indirect optical transitions in shallow etched GaAs/AIGaAs wires, dots and antidots. Semicond. Sci. Technol. 8, 617–621 (1993).
Weiner, J. S. et al. Electron gas in semiconductor multiple quantum wires: spatially indirect optical transitions. Phvs. Rev. Lett. 63, 1641–1644 (1989).
Egeler, T. et al. Anisotropic plasmon dispersion in a lateral quantum-wire superlattice. Phys. Rev. Lett. 65, 1804–1807 (1990).
Singha, A. et al. Two-dimensional Mott–Hubbard electrons in an artificial honeycomb lattice. Science 332, 1176–1179 (2011).
Soibel, A., Meirav, U., Mahalu, D. & Shtrikman, H. Fabrication and transport measurements of honeycomb surface superlattices. Semicond. Sci. Technol. 11, 1756–1760 (1996).
Nadvornik, L. et al. From laterally modulated two-dimensional electron gas towards artificial graphene. New J. Phys. 14, 053002 (2012).
Wang, S. et al. Observation of electron states of small period artificial graphene in nano-patterned GaAs quantum wells. Appl. Phys. Lett. 109, 113101 (2016).
Polini, M., Guinea, F., Lewenstein, M., Manoharan, H. C. & Pellegrini, V. Artificial honeycomb lattices for electrons, atoms and photons. Nat. Nanotech. 8, 625–633 (2013).
Scarabelli, D. et al. Fabrication of artificial graphene in a GaAs quantum heterostructure. J. Vac. Sci. Technol. B 33, 06FG03 (2015).
Czaplewski, D. A., Holt, M. V. & Ocola, L. E. The range and intensity of backscattered electrons for use in the creation of high fidelity electron beam lithography patterns. Nanotechnology 24, 305302 (2013).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2010).
Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Sushkov, O. P. & Neto, A. H. C. Topological insulating states in laterally patterned ordinary semiconductors. Phys. Rev. Lett. 110, 186601 (2013).
Albrecht, C. et al. Evidence of Hofstadter’s fractal energy spectrum in the quantized Hall conductance. Phys. Rev. Lett. 86, 147–150 (2001).
Geisler, M. et al. Detection of a Landau band-coupling-induced rearrangement of the Hofstadter butterfly. Phys. Rev. Lett. 92, 256801 (2004).
Melinte, S. et al. Laterally modulated 2D electron system in the extreme quantum limit. Phys Rev Lett. 92, 036802 (2004).
Žutić, I., Fabian, J. & Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Han, W., Kawakami, R., Gmitra, M. & Fabian, J. Graphene spintronics. Nat. Nanotech. 9, 794–807 (2014).
Acknowledgements
The work at Columbia University was supported by grant DE-SC0010695 from the US Department of Energy Office of Science, Division of Materials Sciences and Engineering, and by the National Science Foundation, Division of Materials Research, under award DMR-1306976. The growth of GaAs/AlGaAs QWs at Purdue University was supported by grant DE-SC0006671 from the US Department of Energy Office of Science, Division of Materials Sciences and Engineering. The growth of GaAs/AlGaAs QWs at Princeton University was supported by the Gordon and Betty Moore Foundation under award GMBF-2719 and by the National Science Foundation, Division of Materials Research, under award DMR-0819860. V.P. acknowledges the European Graphene Flagship (contract no. CNECT-ICT-604391) for financial support and the Italian Ministry of Research (MIUR) through the program ‘Progetti Premiali 2012’ – Project ‘ABNANOTECH’. The authors thank G.P. Watson for technical assistance with the ICP-RIE etching and A. Levy and F. Qiao for discussions.
Author information
Authors and Affiliations
Contributions
S.W. performed ICP-RIE processing and optical experiments. S.W. and L.D. performed numerical calculations. S.W., L.D., Y.Y.K. and A.P. analysed the data. D.S. and S.W. fabricated the AG lattices. G.C.G., M.J.M., K.W. and L.N.P. fabricated the QW samples. S.W., D.S., L.D., Y.Y.K., S.J.W. and A.P. co-wrote the paper with input from other authors. V.P., S.J.W. and A.P. conceived the experiments and supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
About this article
Cite this article
Wang, S., Scarabelli, D., Du, L. et al. Observation of Dirac bands in artificial graphene in small-period nanopatterned GaAs quantum wells. Nature Nanotech 13, 29–33 (2018). https://doi.org/10.1038/s41565-017-0006-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-017-0006-x
This article is cited by
-
Probing semiconductor quantum well qubits and associated Shannon entropy using semi-relativistic quantum mechanics
Optical and Quantum Electronics (2023)
-
An image interaction approach to quantum-phase engineering of two-dimensional materials
Nature Communications (2022)
-
Quantum fluids of light in all-optical scatterer lattices
Nature Communications (2021)
-
Emerging many-body effects in semiconductor artificial graphene with low disorder
Nature Communications (2018)