Abstract
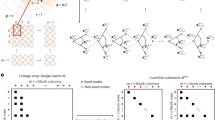
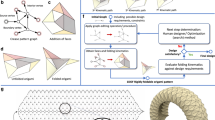
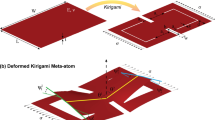
Kirigami tessellations, regular planar patterns formed by partially cutting flat, thin sheets, allow compact shapes to morph into open structures with rich geometries and unusual material properties. However, geometric and topological constraints make the design of such structures challenging. Here we pose and solve the inverse problem of determining the number, size and orientation of cuts that enables the deployment of a closed, compact regular kirigami tessellation to conform approximately to any prescribed target shape in two or three dimensions. We first identify the constraints on the lengths and angles of generalized kirigami tessellations that guarantee that their reconfigured face geometries can be contracted from a non-trivial deployed shape to a compact, non-overlapping planar cut pattern. We then encode these conditions into a flexible constrained optimization framework to obtain generalized kirigami patterns derived from various periodic tesselations of the plane that can be deployed into a wide variety of prescribed shapes. A simple mechanical analysis of the resulting structure allows us to determine and control the stability of the deployed state and control the deployment path. Finally, we fabricate physical models that deploy in two and three dimensions to validate this inverse design approach. Altogether, our approach, combining geometry, topology and optimization, highlights the potential for generalized kirigami tessellations as building blocks for shape-morphing mechanical metamaterials.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Code availability
Computer codes used in this study are available from the corresponding author on request.
References
Grima, J. N. & Evans, K. E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 19, 1563–1565 (2000).
Grima, J. N., Alderson, A. & Evans, K. E. Negative Poisson’s ratios from rotating rectangles. Comp. Methods Sci. Technol. 10, 137–145 (2004).
Grima, J. N., Alderson, A. & Evans, K. E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi B 242, 561–575 (2005).
Rafsanjani, A. & Pasini, D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mech. Lett. 9, 291–296 (2016).
Sussman, D. M. et al. Algorithmic lattice kirigami: a route to pluripotent materials. Proc. Natl Acad. Sci. USA 112, 7449–7453 (2013).
Blees, M. K. et al. Graphene kirigami. Nature 524, 204–207 (2015).
Zhang, Y. et al. A mechanically driven form of Kirigami as a route to 3D mesostructures in micro/nanomembranes. Proc. Natl Acad. Sci. USA 112, 11757–11764 (2015).
Shyu, T. C. et al. A kirigami approach to engineering elasticity in nanocomposites through patterned defects. Nat. Mater. 14, 785 (2015).
Rafsanjani, A. & Bertoldi, K. Buckling-induced kirigami. Phys. Rev. Lett. 118, 084301 (2017).
Konaković, M. et al. Beyond developable: computational design and fabrication with auxetic materials. ACM Trans. Graph. 35, 89 (2016).
Tang, Y. & Yin, J. Design of cut unit geometry in hierarchical kirigami-based auxetic metamaterials for high stretchability and compressibility. Extreme Mech. Lett. 12, 77–85 (2017).
Gatt, R. et al. Hierarchical auxetic mechanical metamaterials. Sci. Rep. 5, 8395 (2015).
Kolken, H. M. & Zadpoor, A. A. Auxetic mechanical metamaterials. RSC Adv. 7, 5111–5129 (2017).
Mitschke, H., Robins, V., Mecke, K. & Schröder-Turk, G. E. Finite auxetic deformations of plane tessellations. Proc. R. Soc. Lond. A 469, 20120465 (2013).
Shan, S., Kang, S. H., Zhao, Z., Fang, L. & Bertoldi, K. Design of planar isotropic negative Poissons ratio structures. Extreme Mech. Lett. 4, 96–102 (2015).
Isobe, M. & Okumura, K. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep. 6, 24758 (2016).
Neville, R. M., Scarpa, F. & Pirrera, A. Shape morphing kirigami mechanical metamaterials. Sci. Rep. 6, 31067 (2016).
Celli, P. et al. Shape-morphing architected sheets with non-periodic cut patterns. Soft Matter 14, 9744–9749 (2018).
Grünbaum, B. & Shephard, G. C. Tilings and Patterns (Freeman, 1987).
Choi, G. P.-T. & Lui, L. M. A linear formulation for disk conformal parameterization of simply-connected open surfaces. Adv. Comput. Math. 44, 87–114 (2018).
Meng, T. W., Choi, G. P.-T. & Lui, L. M. TEMPO: feature-endowed Teichmüller extremal mappings of point clouds. SIAM J. Imaging Sci. 9, 1922–1962 (2016).
Dudte, L. H., Vouga, E., Tachi, T. & Mahadevan, L. Programming curvature using origami tessellations. Nat. Mater. 15, 583–588 (2016).
Acknowledgements
This work was supported in part by the Croucher Foundation (G.P.T.C.), National Science Foundation grant no. DMR 14-20570 (L.M.), DMREF grant no. 15-33985 (L.M.) and EFRI grant no. 18-30901 (L.M.). We thank M. Goldberg for contributing to preliminary numerical work, M. Gazzola for helpful initial discussions, and A. Nagarkar and the Whitesides Group for help with fabrication of some of the models using PDMS.
Author information
Authors and Affiliations
Contributions
L.H.D. and L.M. conceived the research. G.P.T.C., L.H.D. and L.M designed the research. G.P.T.C. and L.H.D. conducted the simulations and built the models. G.P.T.C., L.H.D. and L.M. analysed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
We have filed a patent on our algorithms for kirigami design.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–7, Supplementary Figs. 1–13 and supplementary references.
Rights and permissions
About this article
Cite this article
Choi, G.P.T., Dudte, L.H. & Mahadevan, L. Programming shape using kirigami tessellations. Nat. Mater. 18, 999–1004 (2019). https://doi.org/10.1038/s41563-019-0452-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-019-0452-y
This article is cited by
-
Self-locking Kirigami surfaces via controlled stretching
Communications Engineering (2024)
-
Diffusive kinks turn kirigami into machines
Nature Communications (2024)
-
Curvature tuning through defect-based 4D printing
Communications Materials (2024)
-
Rigid-foldable cylindrical origami with tunable mechanical behaviors
Scientific Reports (2024)
-
Physics-aware differentiable design of magnetically actuated kirigami for shape morphing
Nature Communications (2023)