Abstract
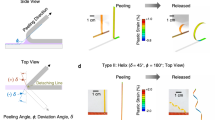
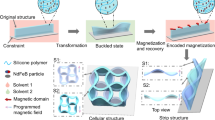
Three-dimensional (3D) structures capable of reversible transformations in their geometrical layouts have important applications across a broad range of areas. Most morphable 3D systems rely on concepts inspired by origami/kirigami or techniques of 3D printing with responsive materials. The development of schemes that can simultaneously apply across a wide range of size scales and with classes of advanced materials found in state-of-the-art microsystem technologies remains challenging. Here, we introduce a set of concepts for morphable 3D mesostructures in diverse materials and fully formed planar devices spanning length scales from micrometres to millimetres. The approaches rely on elastomer platforms deformed in different time sequences to elastically alter the 3D geometries of supported mesostructures via nonlinear mechanical buckling. Over 20 examples have been experimentally and theoretically investigated, including mesostructures that can be reshaped between different geometries as well as those that can morph into three or more distinct states. An adaptive radiofrequency circuit and a concealable electromagnetic device provide examples of functionally reconfigurable microelectronic devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Miura, K. Method of packaging and deployment of large membranes in space. The Institute of Space and Astronautical Science Report 618, 1–9 (1985).
Kuribayashi-Shigetomi, K., Onoe, H. & Takeuchi, S. Cell origami: self-folding of three-dimensional cell-laden microstructures driven by cell traction force. PLoS ONE 7, e51085 (2012).
Randall, C. L., Gultepe, E. & Gracias, D. H. Self-folding devices and materials for biomedical applications. Trends Biotechnol. 30, 138–146 (2012).
Bishop, D., Pardo, F., Bolle, C., Giles, R. & Aksyuk, V. Silicon micro-machines for fun and profit. J. Low Temp. Phys. 169, 386–399 (2012).
Felton, S., Tolley, M., Demaine, E., Rus, D. & Wood, R. A method for building self-folding machines. Science 345, 644–646 (2014).
Ko, H. & Javey, A. Smart actuators and adhesives for reconfigurable matter. Acc. Chem. Res. 50, 691–702 (2017).
Kwok, S. W. et al. Magnetic assembly of soft robots with hard components. Adv. Funct. Mater. 24, 2180–2187 (2014).
Silverberg, J. L. et al. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 345, 647–650 (2014).
Overvelde, J. T. B. et al. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun. 7, 10929 (2016).
Overvelde, J. T. B., Weaver, J. C., Hoberman, C. & Bertoldi, K. Rational design of reconfigurable prismatic architected materials. Nature 541, 347–352 (2017).
Shan, S. et al. Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296–4301 (2015).
Li, X. Y. & Gao, H. J. Smaller and stronger. Nat. Mater. 15, 373–374 (2016).
Silverberg, J. L. et al. Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nat. Mater. 14, 389–393 (2015).
Yang, N. & Silverberg, J. L. Decoupling local mechanics from large-scale structure in modular metamaterials. Proc. Natl Acad. Sci. USA 114, 3590–3595 (2017).
Castle, T. et al. Making the cut: lattice kirigami rules. Phys. Rev. Lett. 113, 245502 (2014).
Castle, T., Sussman, D. M., Tanis, M. & Kamien, R. D. Additive lattice kirigami. Sci. Adv. 2, e1601258 (2016).
Sussman, D. M. et al. Algorithmic lattice kirigami: a route to pluripotent materials. Proc. Natl Acad. Sci. USA 112, 7449–7453 (2015).
Dudte, L. H., Vouga, E., Tachi, T. & Mahadevan, L. Programming curvature using origami tessellations. Nat. Mater. 15, 583–588 (2016).
Lv, C., Krishnaraju, D., Konjevod, G., Yu, H. Y. & Jiang, H. Q. Origami based mechanical metamaterials. Sci. Rep. 4, 5979 (2014).
Schenk, M. & Guest, S. D. Geometry of Miura-folded metamaterials. Proc. Natl Acad. Sci. USA 110, 3276–3281 (2013).
Waitukaitis, S., Menaut, R., Chen, B. G. G. & van Hecke, M. Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114, 055503 (2015).
Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y. & Mahadevan, L. Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110, 215501 (2013).
Al-Mulla, T., & Buehler, M. J. Folding creases through bending. Nat. Mater. 14, 366–368 (2015).
Reis, P. M., Jimenez, F. L. & Marthelot, J. Transforming architectures inspired by origami. Proc. Natl Acad. Sci. USA 112, 12234–12235 (2015).
Cheung, K. C., Tachi, T., Calisch, S. & Miura, K. Origami interleaved tube cellular materials. Smart Mater. Struct. 23, 094012 (2014).
Filipov, E. T., Paulino, G. H. & Tachi, T.Origami tubes with reconfigurable polygonal cross-sections. Proc. R. Soc. A 472, 20150607 (2016).
Filipov, E. T., Tachi, T. & Paulino, G. H. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl Acad. Sci. USA 112, 12321–12326 (2015).
Babaee, S., Overvelde, J. T. B., Chen, E. R., Tournat, V. & Bertoldi, K. Reconfigurable origami-inspired acoustic waveguides. Sci. Adv. 2, e1601019 (2016).
Rogers, J., Huang, Y. G., Schmidt, O. G. & Gracias, D. H. Origami MEMS and NEMS. MRS Bull. 41, 123–129 (2016).
Shenoy, V. B. & Gracias, D. H. Self-folding thin-film materials: from nanopolyhedra to graphene origami. MRS Bull. 37, 847–854 (2012).
Leong, T. G. et al. Tetherless thermobiochemically actuated microgrippers. Proc. Natl Acad. Sci. USA. 106, 703–708 (2009).
Reis, P. M. A perspective on the revival of structural (in)stability with novel opportunities for function: from Buckliphobia to Buckliphilia. J. Appl. Mech. 82, 111001 (2015).
Ge, Q., Dunn, C. K., Qi, H. J. & Dunn, M. L. Active origami by 4D printing. Smart Mater. Struct. 23, 094007 (2014).
Ge, Q., Qi, H. J. & Dunn, M. L. Active materials by four-dimension printing. Appl. Phys. Lett. 103, 131901 (2013).
Ding, Z. et al. Direct 4D printing via active composite materials. Sci. Adv. 3, e1602890 (2017).
Gladman, A. S., Matsumoto, E. A., Nuzzo, R. G., Mahadevan, L. & Lewis, J. A. Biomimetic 4D printing. Nat. Mater. 15, 413–418 (2016).
Raviv, D. et al. Active printed materials for complex self-evolving deformations. Sci. Rep. 4, 7422 (2014).
Kim, J., Hanna, J. A., Byun, M., Santangelo, C. D. & Hayward, R. C. Designing responsive buckled surfaces by halftone gel lithography. Science 335, 1201–1205 (2012).
Na, J. H. et al. Programming reversibly self-folding origami with micropatterned photo-crosslinkable polymer trilayers. Adv. Mater. 27, 79–85 (2015).
Zhang, Y. H. et al. Printing, folding and assembly methods for forming 3D mesostructures in advanced materials. Nat. Rev. Mater. 2, 17019 (2017).
Liu, Y., Genzer, J. & Dickey, M. D. ‘2D or not 2D’: shape-programming polymer sheets. Prog. Polym. Sci. 52, 79–106 (2016).
Liu, Y., Shaw, B., Dickey, M. D. & Genzer, J. Sequential self-folding of polymer sheets. Sci. Adv. 3, e1602417 (2017).
Xu, S. et al. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science 347, 154–159 (2015).
Zhang, Y. H. et al. A mechanically driven form of kirigami as a route to 3D mesostructures in micro/nanomembranes. Proc. Natl Acad. Sci. USA 112, 11757–11764 (2015).
Yan, Z. et al. Mechanical assembly of complex, 3D mesostructures from releasable multilayers of advanced materials. Sci. Adv. 2, e1601014 (2016).
Yan, Z. et al. Controlled mechanical buckling for origami-inspired construction of 3D microstructures in advanced materials. Adv. Funct. Mater. 26, 2629–2639 (2016).
Nan, K. et al. Engineered elastomer substrates for guided assembly of complex 3D mesostructures by spatially nonuniform compressive buckling. Adv. Funct. Mater. 27, 1604281 (2017).
Kim, J. et al. Battery-free, stretchable optoelectronic systems for wireless optical characterization of the skin. Sci. Adv. 2, e1600418 (2016).
Kong, Y. L. et al. 3D printed quantum dot light-emitting diodes. Nano Lett. 14, 7017–7023 (2014).
Fenno, L., Yizhar, O. & Deisseroth, K. The development and application of optogenetics. Annu. Rev. Neurosci. 34, 389–412 (2011).
Kim, T. I. et al. Injectable, cellular-scale optoelectronics with applications for wireless optogenetics. Science 340, 211–216 (2013).
Kim, S. et al. Microstructured elastomeric surfaces with reversible adhesion and examples of their use in deterministic assembly by transfer printing. Proc. Natl Acad. Sci. USA 107, 17095–17100 (2010).
Meitl, M. A. et al. Transfer printing by kinetic control of adhesion to an elastomeric stamp. Nat. Mater. 5, 33–38 (2006).
Acknowledgements
J.A.R. and X.L. acknowledge support from the U.S. Department of Energy, Office of Science, Basic Energy Sciences (DE-FG02-07ER46471). Y.Z. acknowledges support from the National Natural Science Foundation of China (11672152), the National Basic Research Program of China (2015CB351900), the Thousand Young Talents Program of China and the Tsinghua National Laboratory for Information Science and Technology. Y.H. acknowledges the support from the NSF (CMMI1300846, CMMI1400169 and CMMI1534120) and the NIH (R01EB019337). J.W.L. acknowledges support from National Research Foundation of Korea (NRF-2017M3A7B4049466). K.N. acknowledges the support from the Frederick Seitz Materials Research Laboratory Central Research Facilities, University of Illinois, where the majority of the experimental work was carried out.
Author information
Authors and Affiliations
Contributions
J.A.R., Yihui Z. and Y.H. designed and supervised the research; Yihui Z. and H.F. led the structural designs, mechanics modelling, electromagnetic modelling, and design of conceivable electromagnetic device, with assistance from K.B., F.L., Y.L., D.F. and Y.H.; H.F. led the submillimetre-scale experimental work, with assistance from K.B. and X.C.; K.N. led the micro-fabrication work, with assistance from W.B., C.Z., J.W, Y.L., M.H., Z.Y., H.L., Yijie Z., Yutong Z., J.Z. and J.W.L.; W.H., K.N. and W.B. led the design and experimental characterizations of 3D radiofrequency demonstrations, with assistance from M.L. and X.L.; K.N., H.F. and L.L. led the design and experimental realizations of 3D active device demonstrations, with assistance from W.B., C.Z., Y.L. and J.Z.; H.F., K.N., W.B., Y.H., Yihui Z., and J.A.R. wrote the text and designed the figures. All authors commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–4; Supplementary Figures 1–25
Videos
Supplementary Video 1
A morphable mesostructure that can be reconfigured between an ‘octopus’ and a ‘spider’.
Supplementary Video 2
A morphable mesostructure that can be reconfigured among four stable shapes.
Rights and permissions
About this article
Cite this article
Fu, H., Nan, K., Bai, W. et al. Morphable 3D mesostructures and microelectronic devices by multistable buckling mechanics. Nature Mater 17, 268–276 (2018). https://doi.org/10.1038/s41563-017-0011-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-017-0011-3
This article is cited by
-
Preparation of high-resolution micro/nano dot array by electrohydrodynamic jet printing with enhanced uniformity
Scientific Reports (2024)
-
Multilevel design and construction in nanomembrane rolling for three-dimensional angle-sensitive photodetection
Nature Communications (2024)
-
Nanoscale three-dimensional fabrication based on mechanically guided assembly
Nature Communications (2023)
-
Origamic metal-organic framework toward mechanical metamaterial
Nature Communications (2023)
-
Multi-field coupling parameter regulation model of flexible circuit pattern using near-field electrohydrodynamic direct-writing method
The International Journal of Advanced Manufacturing Technology (2023)