Main

The plasma streaming from the Sun interacts with the geomagnetic dipole field of Earth and deforms it into a comet-like shape called the magnetosphere. The solar wind−magnetosphere interaction accelerates particles to relativistic energies and creates mega-ampere electric currents, causing hazards to technology in space and on ground1. The basic dynamic mode within the magnetosphere responsible for the most unpredictable space weather, the substorm2, is a transient solar-wind energy storage and release process within the magnetotail. A substorm includes a global reconfiguration of the magnetotail magnetic field, during which a plasmoid grows and is ejected3. Substorms bear general plasma physical importance as they have been observed in other planetary magnetospheres, at Mercury4, Jupiter5 and Venus6. The process also bears a strong similarity to solar eruptions7.

Substorms, including the processes leading to ejection of plasmoids, are not well understood. The two most compelling frameworks to explain the associated events are the near-Earth neutral line (NENL8) and current disruption models (CD9), which build on fundamental plasma processes of magnetic reconnection and ion-kinetic instabilities, respectively. The NENL model suggests that reconnection severs the plasmoid connection to Earth to eject it tailwards and creates fast Earthward plasma flows that disrupt the magnetotail current. In the CD model, a three-dimensional (3D) plasma instability grows first near the Earth in the transition region between the stretched tail and the dipolar inner magnetosphere. This instability drives steepening waves, leading to current disruption as the tail current cannot be sustained within a strongly oscillating geometry. The current disruption then launches tailward-propagating waves, which later trigger reconnection, plasmoid and fast flows9. As both the current disruption and the plasmoid release occur in only a few minutes, albeit roughly 100,000 km apart, it is extremely challenging to uncover how and why the current disruption and plasmoid ejection take place.

Recognizing the universal nature of substorms, NASA launched the Time History of Events and Macroscale Interactions during Substorms (THEMIS) mission, which is composed of five identical spacecraft on radially aligned orbits within the magnetotail. The main purpose of THEMIS was to resolve the sequence of events during a substorm. Ref. 10 reported the first THEMIS substorm observations, which were taken at the dusk side of the tail spanning a range out to ∼21.5 Earth radii (RE = 6,370 km) away from Earth. These observations were interpreted to support the NENL model; however, they were disputed11.

There are two main problems in interpreting in situ observations. First, using only five vantage points, it is difficult to reconstruct how information flows in the vast tail during a rapid, explosive process initiating at an unknown location and time. Second, within the ionosphere, the events always start from a location that maps to the transition region (for example, ref. 12), not to the location of the reconnection onset10. Since new, more comprehensive missions have not been launched after THEMIS, the substorm process remains elusive.

While numerical models offer an opportunity to study dynamic processes simultaneously across a variety of spatial and temporal scales, two specific substorm characteristics have prevented conclusive modelling so far. First, the simulation domain must be global, that is, large enough to include both dayside and nightside to model the evolution of the magnetosphere as a complete system. Second, the physical description needs to capture and distinguish both reconnection-related and instability-related dynamics. Global magnetohydrodynamic (MHD) simulations can model the entire solar wind–magnetosphere interaction and accurately describe the large-scale implications of reconnection13, even if reconnection in space plasmas involves ion and even electron-scale kinetic effects14. However, global MHD simulations lack the drift physics that steepens the instability waves and leads to the current disruption in the CD model. Thus, global kinetic simulations describing both reconnection and instabilities are needed to distinguish between the NENL and CD models.

While fully kinetic simulations describe both electron and proton distribution functions, hybrid approaches treat protons kinetically and electrons as a charge-neutralizing fluid15,16. Global fully kinetic simulations are not computationally feasible, but global hybrid approaches have recently become available. In this Article, we report on the first 3D ion-kinetic simulations that reproduce a tail-wide plasmoid and a global reconfiguration of the tail magnetic topology, including a description of both reconnection and ion-kinetic instabilities.

The Vlasiator simulation (see Vlasiator for details) presents a 6D global hybrid-Vlasov modelling of the solar wind–magnetosphere coupling with 3D real space and 3D velocity space16,17. Magnetic reconnection occurs due to numerical diffusion, similarly as in the state-of-the-art MHD codes13, while Vlasiator additionally captures Hall physics, which is beyond the ideal MHD description. The ion-kinetic drift instabilities are described due to resolving the 3D ion velocity distribution functions in every spatial grid cell of the simulation. In this Article, we show results of a global 6D simulation carried out with the simplest possible driving, including constant solar wind density and speed and steadily southward interplanetary magnetic field reconnecting with the geodipole field. Vlasiator uses Earth’s actual dipole strength, which makes the temporal and spatial scales as well as time evolution directly comparable to in situ space observations.

How the magnetotail erupts

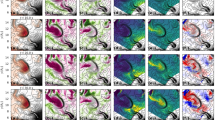
Figure 1 and Supplementary Video 1 show the evolution of the current sheet in the tail, focusing on magnetic topology in zoomed snapshots. We show proxies of x- and o-topology lines that are associated with reconnection and magnetic islands, respectively. We first scrutinize Fig. 1g, showing an o topology (green) from dawn to dusk, co-located with a strong current density. Earthwards and tailwards of the o topology, there are tail-wide x lines (magenta), co-located with a tail-wide flow reversal (yellow) at the Earthward edge, all signatures suggesting reconnection. The o topology separates southward and northward magnetic-field regions (white and black grid, respectively). This tail-wide structure, with the o topology as its central axis, is interpreted as a plasmoid flux rope18.

Fig. 1: Snapshots zooming to the tail current sheet.
figure 1

a–g, The panels are given in the Geocentric Solar Ecliptic coordinate system, where X points sunwards, the Y axis is in the ecliptic plane and positive towards the dusk and the Z axis completes the system and is positive northwards. The shown plasma sheet surface is given by the condition Br = 0, where Br is the radial magnetic field B component. Snapshots are given at 1,300 s (a), 1,350 s (b), 1,400 s (c), 1,428 s (d), 1,443 s (e), 1,450 s (f) and 1,470 s (g) (see the whole sequence in Supplementary Video 1). Colour gives the current density J. The thick yellow contour shows the plasma flow reversal (V'x = 0) between the Earthward and tailward flow regions, after subtracting the tailward lobe velocity (see Methods, ‘Applicability’). Magenta and green contours are neutral line proxies where Br = 0 and Bz = 0. The derivative of Bz is used as a proxy to classify the neutral line as x and o topologies, such that the radial gradient ∂Bz /∂r is negative (green) and positive (magenta), respectively, at o and x topologies. On top of the o-topology green contours, part of the magnetic-field lines are additionally depicted with green thin lines to further illustrate the o topology. The dominant reconnection line is assumed to exist where the magenta (∂Bz/∂r > 0) and yellow contours are approximately co-located, while those locations where only the magenta line exists are either local reconnection or, for example, dipolarization fronts29. The background grid shows the coordinates but also the magnetic-field topology: the black grid shows areas where the magnetic field is northwards, and the white grid shows the areas where it is southwards. The arrows are referred to in the text. The dashed magenta lines in d indicate the locations of the cuts at fixed X and Y coordinates, presented in Fig. 2.

Full size image

Snapshots in Fig. 1a–g show how the tail-wide flux rope develops and detaches. Figure 1a is selected as the starting point for the event sequence since at this time, the magnetotail magnetic topology is relatively simple. The current density is high (∼8 nA m−2) throughout the tail except along a persistent, radially aligned current sheet fold at Y ≈ 5 RE. While Fig. 2 will show the tail reconnection characteristics in detail, in Fig. 1a both the reconnection x-topology proxy (magenta) and the flow reversal (yellow) suggest that the dominant reconnection occurs roughly at X = −15 RE from dawn to dusk. There are also some more localized x lines in the tail. The x-line proxy shows a similar overall structure as in previous MHD simulations, where the x line includes elongated wings near the flanks, connected eventually to the dayside large-scale x line19.

Fig. 2: Cuts through the current sheet in two planes at t = 1,428 s.
figure 2

a–e, Cuts in the XZ plane at fixed Y = −3.5 RE. f–j, Cuts in the YZ plane at fixed X = −13 RE. All units are SI (International System of Units). The cuts are taken along the magenta dashed lines shown in Fig. 1d. a,f, Plasma velocity Vx (a) and Vy (f) component, with the background lobe velocity subtracted. b,g, Electric field Ez component. c,h, Temperature anisotropy parameter as defined from the velocity distributions, defined with respect to the magnetic field in the perpendicular and parallel directions of temperature T (T⊥ and T||, respectively). d,i, Plasma number density n. e,j, Perpendicular slippage (V⊥ −V(E × B))/VA, where V⊥ is velocity perpendicular to the magnetic field, VA is the Alfvén velocity and E and B are electric and magnetic fields, respectively. The slippage characterizes ion demagnetization21. Velocity streamlines are overplotted in a and f. Magnetic field lines are overplotted in all other panels. The green circles and magenta crosses are the reconnection proxy positions; definitions are given in connection to Fig. 1.

Full size image

Figure 1b shows the formation of two local reconnection regions near both flanks (Y ≈ 12 RE and Y ≈ −6 RE, white arrows). The tail-wide x line is roughly at X ≈ −18 RE (14 RE) in the dawn (dusk) sector. The two local flank reconnection regions form a southward magnetic field topology, as shown by the white grid enclosed by the reconnection proxy contours. At this time (t = 1,350 s), the tail current sheet starts to show flapping oscillation (ripples in the plotted surface), which is examined in detail in Fig. 3. In Fig. 1c (t = 1,400 s), the dawn flank local reconnection site has merged with the flank x line (white arrow). The intensifying flapping waves extend radially from their Earthward edge in the transition region to cover the entire plotted current sheet. Figure 1d shows that the two flank flux ropes A and B have increased in size, moved tailwards and towards the plasma sheet centre but are topologically still separated. This can be seen from the magnetic-field topology, which is southwards in connection to the flux ropes but northwards near Y = 0 RE. The flapping waves have intensified to a single fold near Y = 0 RE, and the current density has decreased on this fold starting from the transition region (white arrow). Figure 1e shows that at time t = 1,443 s the o line of the flux rope A in the dusk flank is also merging with the flank x line (black arrow). The central current sheet fold shows a considerable decrease of the current density in a narrow radially coherent channel. Figure 1f shows the two flank flux ropes merged in the centre into a tail-wide flux rope with a single topology. This flux rope detaches and at the same time relaxes the current sheet folds and flaps.

Fig. 3: Current-sheet flapping, ion distribution functions and dispersion analysis.
figure 3

a–e, The current sheet at X = −14 RE in the YZ plane at simulation times t = 1,340 s (a), 1,360 s (b), 1,380 s (c), 1,400 s (d) and 1,447 s (e). Colouring gives the current density J, and the red crosses mark the positions at which the ion velocity distributions from the current sheet in panels f–i are given. f–i, Ion velocity distributions in the current sheet at the position shown with a red cross in panels a–d at simulation times t = 1,340 s (f), t = 1,360 s (g), t = 1,380 s (h) and t = 1,400 s (i). The distributions are plotted in the same plane as the current sheet plots. The thick cross and red circle in panels g–i refer to the drift and thermal velocities that are required in the instability analysis in Methods. j, The positions of the flapping wave extrema as a function of run time shown as coloured dots in panels a–e. Wave maxima and minima are followed in time as the flapping waves evolve. The temporal separation of the wave extrema in panel j gives half of the wave period, while the spatial separation gives half of the wavelength. Using the average positions of the wave extrema in time and space, we get their frequency and wavelength, which are plotted in panel k as coloured dots. The horizontal error bars represent the standard error of the mean (SEM) between adjacent extrema along the time axis, while the vertical error bars represent the SEM evaluated using the adjacent extrema along the Y axis. The sample sizes to evaluate the SEMs are given in the vicinity of each point (see the legends in panel k). The red solid, dashed and dotted lines correspond to the real frequency of the instability analysis using the ion distributions in panels g–i. The black solid, dashed and dotted lines are the growth rate of the drift kink instability obtained using linear kinetic theory (see Methods for details), using the distributions in panels g–i.

Full size image

In Fig. 2 we examine whether the proxies are associated with signatures of symmetric reconnection examined previously in observations20 and simulations21. Pseudocolour plots are taken at t = 1,428 s along the two perpendicular profiles that are depicted in Fig. 1d (dashed magenta lines). The left-hand plots in the XZ plane at Y = −3.5 RE show that the reconnection proxies in Fig. 1d indeed are reconnection lines, as along the cut there are two ion diffusion regions at the positions of the proxies, that is, at X ≈ −14 RE and X ≈ −20 RE. These two reconnection sites are visible as sources for diverging plasma flows (Fig. 2a), surrounded by bipolar Hall electric field Ez that points towards the neutral plane (Fig. 2b). The panels also show a clear large-density flux rope (Fig. 2d) centred at about X ≈ −17 RE, co-located with the o-topology proxy in Fig. 1d. On both sides of the o line are large perpendicular temperatures (Fig. 2c) as well as demagnetization of ions (Fig. 2e), showing that the ions are meandering along the x lines. This is a clear signature of ion diffusion regions21. In addition, the cut along the Y axis at X = −13 RE (right plots) shows clear reconnection signatures. Especially, the right-hand plots show that the o-topology line at Y ≈ −13 RE at the flank is clearly an o topology. This o line was formed when the local reconnection region within the tail merged with the flank neutral line (Fig. 1c,d and Supplementary Video 1). Figure 2 shows that this magnetic island is formed within a Y-type null topology seen, for example, at the foot of coronal mass ejections22.

Figure 3 provides evidence that demagnetized ions originating from reconnection cause the flapping oscillations by excitation of the drift kink instability. Figure 3a–e presents the current density in the YZ plane at X = −14 RE at different stages of flapping wave evolution, showing growth (Fig. 3a,b), dawn–dusk propagation (Fig. 3c,d) and collapse into the fold (Fig. 3e). At t = 1,447 s, the fold geometry has become so steep that it does not support the current anymore, as the current in the fold is strongly disrupted and reduced to ∼3 nA m−2 (Fig. 3e). The red crosses in Fig. 3a–d show the position at which ion velocity distributions in Vy − Vz space are given in Fig. 3f–i. These distributions first show a perpendicular crescent-shaped beam (Fig. 3f) like the ones formed due to meandering demagnetized ions originating from reconnection23. This demagnetized ion population carries the non-adiabatic current that is required for the development of the drift kink instability (Methods). As the flapping waves develop, the growing instability thermalizes the demagnetized ions, and they merge with the core ions.

We quantify the wavelength and period of the flapping waves by tracing the local extrema of the current layer in space and time (Fig. 3j). For the obtained values of wavelength and period, we calculate the wave vector and frequency and compare them with the values predicted in the framework of the linear theory (see Fig. 3k for the dispersion plot and Methods for the details of the drift kink instability). Figure 3k shows that the typical wavelength λ ≈ 1.6 RE and period T ≈ 40 s give the wavenumber kRE ≈ 3.9 and frequency f ≈ 0.025 Hz, which are compatible with satellite-based observations of the flapping waves24. Figure 3k shows that the simulation-quantified dispersion using the wave extrema and the analytical dispersion relation agree, giving strong evidence that the flapping waves are generated by the drift kink instability due to the demagnetized ions in the reconnecting thin current sheet, and the nonlinear evolution of these waves leads to the disruption of the current.

How previous findings fit into the simulation picture

The presented results provide a framework of how a combination of processes act together to eject a tail plasmoid in a global simulation. Figure 4 shows a simplified schematic of the events. Three discoveries follow from the analysis of this 6D global ion-kinetic simulation of Earth’s magnetosphere: (1) both magnetic reconnection and current disruption are required to generate the topological reconfiguration spanning across the entire magnetotail obtained with the formation and release of a tail-wide plasmoid, (2) the near-simultaneous observations involved in launching the plasmoid across large distances in the magnetotail can be explained by the concerted action facilitated by current-sheet flapping and (3) the current-sheet flapping can be explained by reconnection-generated demagnetized ions that are unstable to the drift kink instability.

Fig. 4: Simplified schematics showing the events within the tail current sheet leading to the eruption of the tail-wide plasmoid.
figure 4

a, The situation within Fig. 1b, showing the two local reconnection regions Earthward and tailward of the dominant x line. Magnetic field topology is given, with ⊙ and ⊗ symbols representing outward and inward directions with respect to the plane and corresponding to Bz > 0 and Bz < 0, respectively. b, The situation within Fig. 1c, where the dusk flank local flux rope is mainly Earthward of the dominant x line. The flapping begins. c, The situation within Fig. 1d, where the flapping waves have evolved into the strong central fold in the noon–midnight meridional plane. The flux ropes have grown and moved tailwards and towards the centre of the plasma sheet. d, The situation within Fig. 1g, where the large tail-wide plasmoid has been formed from the two local flank flux ropes. Their merging in the centre current sheet was enabled by the current disruption within the central fold. In all panels, the position of the dominant x line is a result of a competition between two x lines. The one that is stronger diverts flow, and hence the global flow reversal changes position.

Full size image

Our results combine the NENL and CD frameworks into the context of the ion-kinetic tail beyond the few points at which the observations supporting each framework have been made. The global tail reconfiguration and the plasmoid release occur because two strong reconnection sites and associated flux ropes in the magnetotail flanks propagate towards the tail centre and merge to form a tail-wide plasmoid. Simultaneously, in the inner tail, the midnight-sector current sheet is disrupted radially as a consequence of steepening current-sheet flapping. The disruption starts in the transition region and propagates tailwards. In the simulation, reconnection and current disruption both occur simultaneously but in different parts of the vast tail, explaining the ambiguity in the observations and the persistence of seemingly contradicting paradigms. The key reason such conclusions have not been reached before is that in situ observations have not simultaneously covered the dawn–dusk and along-the-tail directions.

Relating the simulation dynamics to the THEMIS observations that were made in the dusk flank off the noon–midnight meridional plane10, the Vlasiator results show a clear NENL-type sequence of events: reconnection and fast flows (Fig. 2) before a major reconfiguration. However, within the noon–midnight meridian, a current disruption starts from the transition region and spreads outwards before the large-scale reconnection releases the plasmoid, in line with the CD scenario9. The cause for the current disruption is not the fast flows from the reconnection, as thought within the NENL paradigm (for example, ref. 12). The current disruption starts via a kinetic instability in the inner magnetosphere, as suggested by the CD model, but requires reconnection-generated demagnetized ions that initiate a large-scale current sheet flapping, which steepens to disrupt the current. The simulation shows that there is no new reconnection in the tailward direction triggered by the current disruption, as the CD helps only to release the plasmoid from the already-existing reconnection sites.

Typically, the large-scale magnetotail responds rapidly within temporal scales that are faster than typical wave speeds. A repeatable system characteristic is that the effects included in the plasmoid release are seen from the near-geostationary distance to the mid-magnetotail 100,000 km away within only a few minutes. The Vlasiator simulation reveals the key role played by the current sheet flapping: The entire tail develops coherent flapping motion and folds, which allow the tail to act in concert and facilitate fast information flow. Furthermore, the simulation confirms that flapping waves are indeed tail-aligned elongated structures25.

The origin of the flapping is not established in the present literature, as both external26 and internal drivers27 have been suggested as possible causes. The simulation results conclusively rule out solar wind variations as the sole drivers for the current sheet flapping as our run is carried out with steady solar wind. The observed cross-tail propagation direction of the flapping waves is mostly towards the flanks27, while our simulation shows predominantly a duskward propagation. However, our results do not necessarily contradict previous findings on the propagation direction as this simulation covers only one solar wind driver. Subsequent studies are needed to further address this topic.

The Vlasiator results also have wider implications. The recent decade of multi-satellite missions, such as THEMIS that has interspacecraft separations suited for large-scale studies or the Magnetospheric Multiscale Mission that focuses on electron-scale processes, have paved the way for planning of truly comprehensive missions that could resolve the critically important mesoscale processes such as those discussed in this Article. The Vlasiator results can be used in determining the key regions, interspacecraft distances and observational requirements necessary to tackle the tail eruption with in situ observations. Furthermore, our results can help interpret the most often single-spacecraft measurements in planetary space environments (for example, refs. 4,28). The interplay of reconnection and kinetic instabilities can have important implications for our interpretation of remote-sensing observations from the Sun.

Methods

Vlasiator

Vlasiator16,17 (https://helsinki.fi/vlasiator) simulates the plasma dynamics using a hybrid-Vlasov model in six-dimensional (6D) phase space, containing 3D real space and 3D space for proton velocity distributions. This approach treats electrons as a charge-neutralizing fluid through Ohm’s law, including the Hall and electron pressure gradient terms, but does not take into account electron kinetic effects in which electron dynamics modify the magnetic fields. However, the ion-kinetic effects are described in detail using a noiseless representation of the ion velocity distribution in a grid, without relying on particle statistics as in the complementary hybrid particle-in-cell schemes15. Each 3D grid cell in the ordinary space includes a 3D velocity space, where the proton distribution function is propagated in time using the Vlasov equation. The electromagnetic field in the ordinary space is updated using the velocity moments, making the approach self-consistent. Progressing from ref. 16, the 6D run presented here was made possible by enabling static adaptive mesh refinement17 for the spatial space, where the plasma sheet is filled with a finer spatial grid than is used in the solar wind. This is standard practice in global MHD simulations.

The simulation volume in the run presented here extends from X = −111 RE in the magnetotail to X = 50 RE in the solar wind and ±58 RE in the Y and Z directions. The inner shell of the magnetospheric domain, approximated with a perfectly conducting sphere, is at 4.7 RE. Earth’s unscaled dipole, centred at the origin, is used as a boundary condition, and an infinite conductivity is used at the ionospheric boundary. Solar wind conditions are input to the simulation at the Sunward wall of the simulation box. The interplanetary magnetic field is (0,0, − 5) nT, the solar-wind density is 106 m−3, the solar wind velocity is (−750,0,0) km s−1 and the solar wind velocity distribution is initialized as Maxwellian. Fast solar wind values were chosen to speed up the initialization phase of the run. Other walls of the simulation box apply Neumann copy conditions. The total length of the simulation is 1,506 s. It is initialized by running the solar wind parameters from t = 0 s, and the first 500 s during which the solar wind first flushes through the simulation box are omitted from the results.

Resolution

Vlasiator’s high-quality ion-kinetic description is enabled due to three selected modelling strategies. First, the resolution in the ordinary space is adaptive and varies from 0.16 RE to 1.26 RE, being finest in the plasma sheet and near Earth and coarsest in the solar wind. The velocity space resolution is 40 km s−1, and ion distribution functions are solved in all spatial grid cells within the simulation, and they give rise to the ion-kinetic physics. Second, in most cases, the ion-kinetic physics arises from the high-energy ions that have a large ion gyroradius. For example, the ion–ion beam instability in the foreshock, responsible for the foreshock waves, arises from the suprathermal ion beam population reflected at the bow shock30. The suprathermal ions, which give the free energy for the instability growth, are resolved in detail both in the spatial space, due to the large gyroradius, and in the velocity space due to the noiseless representation of the proton phase space density computed in a grid, not constructed from particle statistics. The outcome is that ion-kinetic physics that arise from suprathermal ions is reproduced even with a coarser spatial grid resolution because the velocity space is well resolved31. Third, in contrast to hybrid particle-in-cell simulations that need a fine grid resolution to compensate for the particle noise, Vlasiator’s grid-based methods and especially the use of slope limiters, in both the spatial and velocity space, allow use of a coarser grid that still describes the instability-driven waves in detail.

Applicability

The results are valid insofar as electron dynamics contributing to the electromagnetic field and the absence of the dynamic ionosphere are not the main drivers in launching the tail-wide plasmoid. Treating electrons through Ohm’s law is a good approximation everywhere except within the reconnection electron diffusion region32, which amounts to a tiny fraction of the entire magnetospheric domain. Vlasiator treats reconnection through numerical resistivity, similarly as in global MHD simulations.

The lack of a dynamic ionosphere prevents the full Dungey cycle of field lines. The dayside magnetic reconnection opens flux that is dragged to the nightside, but since the field lines do not move at the infinitely conducting ionospheric boundary, there is no return flow towards the dayside. In reality, the sunward convection in the tail introduces a sunward velocity component for plasma, which is absent in the simulation run. As a consequence, the tail has a constant anti-sunward plasma flow coming from the solar wind, and the only sunward flow is created by magnetic reconnection. Therefore, a simulation without a dynamic ionosphere represents only half of the Dungey cycle. This indicates that the run describes a situation where the tail disruption occurs rapidly as a consequence of a fast magnetic erosion at the dayside. Such conditions occur during stormtime; however, during such times, the plasma sheet properties are still representative33. The lack of dynamic ionosphere also prevents studying the magnetosphere–ionosphere coupling during tail eruptions, for example, the formation of the current wedge coupling the tail current to the ionosphere. We conclude that the presented run set-up can describe the events leading to the plasmoid release and global reconfiguration from the tail perspective.

We also note that these results concern one set of solar wind conditions. So far, we have two other runs that have similar boundary conditions within the ionosphere but have different solar wind conditions representing stronger driving. In the other runs, the tail goes into a more directly driven mode, where a tail-wide plasmoid does not develop; rather there is continuous strong reconnection throughout the dominant x line. The two other runs do not include similar flapping waves as shown in this Article. This provides one additional argument emphasizing that flapping is required to develop a current disruption. However, additional runs are needed to fully clarify this point.

Linear kinetic theory for drift kink instability

In this section, we describe in detail the analysis performed to explain the flapping oscillations within the magnetotail current sheet. First, we describe the properties of the flapping waves in the simulation. The wave vector of the current layer oscillations is in the dawn–dusk direction, coinciding with the direction of the general current in the current sheet. The properties of the wave are ∼1 RE amplitude, ∼1.6 RE wavelength and ∼40 s period, corresponding to the phase velocity of ∼270 km s−1. Since the oscillations are clearly larger than the Larmor scale, the fluctuations are of an electromagnetic nature. Thus, we analyse the instability that causes the flapping using the electromagnetic formalism proposed for the drift kink instability of the current layer34.

As the initial unperturbed state without the flapping oscillation, we consider a Harris current sheet that has a width L, with a density profile n(z) along the Z coordinate, which is normal to the current sheet in the unperturbed state:

$$n\left(z\right)={n}_{0}\cos {h}^{-2}\left(\frac{z}{L}\right),$$

where n0 is the peak current in the Harris current sheet. We assume that the population carrying the Harris current f0 is a drifting Maxwellian:

$${f}_{0}=n\left(z\right)\sqrt{{\left(\frac{m}{2{\pi}{k}_{{\mathrm{B}}}T}\right)}^{3}}\cdot \exp \left[-\frac{m}{2{k}_{{\mathrm{B}}}T}\left({v}_{{\mathrm{x}}}^{2}+{\left({v}_{{\mathrm{y}}}-u\right)}^{2}+{v}_{{\mathrm{z}}}^{2}\right)\right],$$

Here, m and T are ion mass and temperature, respectively, kB is the Boltzmann constant, vx, vy, vz are the three components of the ion thermal velocity and u is the drift velocity directed along Y.

We then consider a perturbation of the distribution function f1 and linearize with the Vlasov equation

$$\frac{{\mathrm{d}}{f}_{1}}{{{\mathrm{d}}t}}=-\frac{q}{m}\left(-\frac{\partial {{\bf{A}}}_{1}}{\partial {{t}}}+\left[{\bf {v}}\times \nabla \times {{\bf{A}}}_{1}\right]\right)\cdot \frac{\partial {f}_{0}}{\partial v}$$
(1)

In equation (1), q is the ion charge, v is plasma velocity and the perturbed magnetic field B1 is expressed using the perturbed vector potential A1 (B1 = ∇ × A1). The electrostatic part of the perturbed potential can be neglected because the frequency of the perturbation is much lower than the plasma frequency. We also neglect the displacement current because the phase velocity of the waves is much less than the speed of light. The Ampère’s law can be written as

$$\Delta {{\bf{A}}}_{1}=-{{\rm{\mu }}}_{0}{{\bf{J}}}_{1},$$
(2)

where \({\mu }_{0}\) is the vacuum permeability and \({{\bf{J}}}_{1}\) is the perturbed current density.

Following the drift kink instability discussion34, we approximate the system as 2D with spatial dependence along Y and Z (∂/∂x = 0). We also consider the Coulomb gauge that in the 2D approximations becomes (∂yAy + ∂zAz = 0). This leads to two independent polarizations: Ay = Az = 0 and Ax = 0. As discussed in ref. 34, the first polarization is physically more important. Hence, in the following, we will consider the first polarization only. After a straightforward transformation, we obtain the linkage for the A1y component of the perturbed potential and the perturbed distribution function:

$$\frac{{\mathrm{d}}{f}_{1}}{{{\mathrm{d}}t}}=\frac{q\,{f}_{0}}{m}\left[\frac{d}{{{\mathrm{d}}t}}{{\mathrm{A}}}_{1{\mathrm{y}}}u-{v}_{{\mathrm{y}}}{\partial }_{t}{{\mathrm{A}}}_{1{\mathrm{y}}}+u{v}_{{\mathrm{y}}}{\partial }_{{\mathrm{y}}}{{\mathrm{A}}}_{1{\mathrm{y}}}\right].$$
(3)

The Ampère’s law (equation (2)) and equation (3) form a complete system. We assume a harmonic dependence along Y and time, while the dependence along Z is such that the perturbation is well behaved:

$${{\mathrm{A}}}_{1{\mathrm{y}}}\left(\,y,z,t\right)={\hat{{\mathrm{A}}}}_{1{\mathrm{y}}}\left(z\right)\exp \left(i\omega t-{iky}\right)$$
$${f}_{1}\left(\,y,z,t\right)={\hat{f}}_{1}\left(z\right)\exp \left(i\omega t-{iky}\right),$$

where \({\hat{{\mathrm{A}}}}_{1{\mathrm{y}}}\) and \({\hat{f}}_{1}\) are the magnitudes of the perturbations, while ω and k are the frequency and wave vector.

After integration of equation (3) along straight unperturbed trajectories35, we obtain the explicit form of the perturbed distribution amplitude:

$${\hat{{f}_{1}}}=\frac{q\,{f}_{0}{\hat{{\mathrm{A}}}}_{1{\mathrm{y}}}}{{k}_{B}T}\left(u-{v}_{{\mathrm{y}}}\frac{\omega -{ku}}{\omega -k{v}_{{\mathrm{y}}}}\right).$$
(4)

Integration over the velocity space gives the perturbed current \({{\mathrm{J}}}_{{\mathrm{y}}}=q\int {v}_{{\mathrm{y}}}{f}_{1}{{\mathrm{d}}v}\), and after substitution into equation (2), we obtain the equation for \({\hat{{\mathrm{A}}}}_{1{\mathrm{y}}}\) giving the dispersion equation:

$$\frac{{{\mathrm{d}}}^{2}{\hat{{\mathrm{A}}}}_{1y}}{{\mathrm{d}}{z}^{2}}-{k}^{2}{\hat{{\mathrm{A}}}}_{1y}=-{\mu }_{0}\left[{\hat{{\mathrm{J}}}}_{{{\mathrm{ad}}}}+{\hat{{\mathrm{J}}}}_{{\mathrm{n}}}\varTheta \left(z\right)\right],$$
(5)

where \(\varTheta \left(z\right)\) is an indicator function and \({\hat{{\mathrm{J}}}}_{{{\mathrm{ad}}}}\), \({\hat{{\mathrm{J}}}}_{{\mathrm{n}}}\) are the adiabatic and non-adiabatic currents, respectively, given by

$${\Theta }(z)=\left\{\begin{array}{ll}1, & {\rm{if}}\,|z|\le {d}_{{\mathrm{i}}}\\ 0, & {\rm{if}}\,|z| > {d}_{{\mathrm{i}}}\end{array}\right.$$

where \({d}_{{\mathrm{i}}}=\sqrt{\frac{m}{{\mu }_{0}{n}_{0}{q}^{2}}}\) is the ion inertial length.

$${\hat{{\mathrm{J}}}}_{{{\mathrm{ad}}}}={\hat{{\mathrm{A}}}}_{1{\mathrm{y}}}\frac{2}{{L}^{2}}\cos {h}^{-2}\left(\frac{z}{L}\right)$$

and

$$\begin{array}{c}{\hat{{\mathrm{J}}}}_{{\mathrm{n}}}=\frac{q{\hat{{\mathrm{A}}}}_{1y}}{{k}_{B}T}n\left(z\right)\sqrt{\frac{m}{2{k}_{B}T}}\frac{\omega -{ku}}{k}\cdot \left[-\frac{{v}^{2}}{2}\left(\frac{\omega -{ku}}{{kv}}\right)Z{^\prime} \left(\frac{\omega -{ku}}{{kv}}\right)-\right.\\ \left.-{uvZ}{^\prime} \left(\frac{\omega -{ku}}{{kv}}\right)+{u}^{2}Z\left(\frac{\omega -{ku}}{{kv}}\right)\right].\end{array}$$

In the Jn definition, \(Z\left(\xi \,\right)=\frac{1}{\sqrt{\pi }}{\int }_{-{\rm{\infty }}}^{+{\rm{\infty }}}\frac{{e}^{-{x}^{2}}}{x-\xi }{{\mathrm{d}}x}\) is the plasma dispersion function and \({Z}^{{\prime} \left(\xi \,\right)}=-2\left[1+\xi Z\left(\xi \,\right)\right]\) is its derivative; ξ is a substitution variable representing a function of ω, k, u.

The ion non-adiabatic currents can be directly compared with hybrid simulations because the real current sheet in the magnetotail has a small normal component that maintains the magnetization of electrons36. Due to the linear dependence of currents \({\hat{{\mathrm{J}}}}_{{{\mathrm{ad}}}}\) and \({\hat{{\mathrm{J}}}}_{{\mathrm{n}}}\) on \({\hat{{\mathrm{A}}}}_{1{\mathrm{y}}}\), equation (5) is a Helmholtz equation that has two free parameters, u and v, the plasma drift velocity and thermal velocity, respectively. The solution of this equation is reduced to finding eigenvalues for frequencies providing the final dispersion relation shown in Fig. 3k. Due to the complex nonlinear dependence Jn(ω), we solve equation (5) numerically with the shooting method37. As an input to the shooting method, we use values of the plasma drift velocity u = [223, 247, 119] km s−1 and thermal speed v = [783, 827, 757] km s−1 estimated from the velocity distribution functions in Fig. 3g–i. In Fig. 3g–i, the value of u is marked by a red cross at the centre of a circle of radius v. The width of the current layer is L = 2,000 km, corresponding to 2.3 di, where di = 865 km is calculated for density within the current layer n0 = 0.7·105 m−3.