Abstract
Deglacial transitions of the middle to late Pleistocene (terminations) are linked to gradual changes in insolation accompanied by abrupt shifts in ocean circulation. However, the reason these deglacial abrupt events are so special compared with their sub-glacial-maximum analogues, in particular with respect to the exaggerated warming observed across Antarctica, remains unclear. Here we show that an increase in the relative importance of salt versus temperature stratification in the glacial deep South Atlantic decreases the potential cooling effect of waters that may be upwelled in response to abrupt perturbations in ocean circulation, as compared with sub-glacial-maximum conditions. Using a comprehensive coupled atmosphere–ocean general circulation model, we then demonstrate that an increase in deep-ocean salinity stratification stabilizes relatively warm waters in the glacial deep ocean, which amplifies the high southern latitude surface ocean temperature response to an abrupt weakening of the Atlantic meridional overturning circulation during deglaciation. The mechanism can produce a doubling in the net rate of warming across Antarctica on a multicentennial timescale when starting from full glacial conditions (as compared with interglacial or subglacial conditions) and therefore helps to explain the large magnitude and rapidity of glacial terminations during the late Quaternary.
Similar content being viewed by others
Main
A multitude of ice-core and marine records show that the past 800,000 years of Earth’s history were dominated by global-scale alternations between glacial and interglacial conditions with a high degree of nonlinearity in the climatic response to gradual external forcing1,2. This is particularly relevant for glacial terminations, which are thought to be driven by relatively weak insolation forcing due to changes in Earth’s orbital configuration3,4. In this context, it has been proposed that disruptions to circulation patterns in the coupled atmosphere–ocean system might have acted to accelerate Antarctic warming and the outgassing of CO2 from the Southern Ocean (SO) to cross a critical level necessary to maintain interglacial conditions at a global scale5,6,7. A possible mechanism to reach such a point is an abrupt weakening of the Atlantic meridional overturning circulation (AMOC) and a corresponding reduction of northward oceanic heat transport associated with SO and Antarctic warming, according to the bipolar-seesaw concept8,9,10, which has been detected in a wide spectrum of models11,12. However, since abrupt oscillations between relatively weak and strong AMOC states and corresponding SO changes are thought to be a ubiquitous feature of millennial-scale climate variability throughout most glacial periods13,14, it is open to question what facilitates such a strong temperature response during deglaciation (Fig. 1).
Interglacial and glacial water-mass configurations
The large-scale meridional water-mass distribution in the modern ocean is characterized by deep waters originating in the North Atlantic (North Atlantic Deep Water; NADW) and the SO (Antarctic Bottom Water; AABW). These water masses are connected by mixing processes and wind-driven upwelling within the SO15,16,17,18. AABW represents the densest water mass in the modern ocean due to its low temperature (AABW is relatively fresh and cold compared with the overlying NADW)18,19. Only at great depth does the pressure dependence of the thermal expansion coefficient in the equation of state (the thermobaric effect) mean that the warmth of NADW makes it less dense than AABW20. Thus, a reduction in the temperature contrast between the two water masses will tend to destabilize the water column, ultimately resulting in NADW replacing AABW as the deepest water mass.
With respect to ocean temperature, the most accurate/robust evidence for glacial ocean cooling on a global scale stems from noble gases trapped in ice cores. Bereiter et al.21 show that mean ocean cooling (2.5 ± 0.24 °C) was greater than the maximum possible cooling of AABW, since modern AABW has a temperature of −0.88 °C22 and seawater has a freezing point of about −2 °C. Of particular relevance to our study is the implication that ‘warmer’ water masses such as NADW and intermediate water masses within the Southern Atlantic must have cooled to a greater extent than AABW23. This implies that thermal deep-ocean stratification in the glacial ocean was weaker than it is today. In a hypothetical scenario with no change to the salinity distribution, we can see that such heterogeneous cooling of the glacial ocean could lead to an unstable water column (Extended Data Fig. 1), and yet proxy reconstructions suggest that the glacial version of AABW maintained its position as the deepest water mass at least in the South Atlantic region24,25. Therefore, something probably acted to compensate for the loss of stability from thermal stratification in the glacial ocean.
Indeed, other proxy evidence26,27 suggests that the salinity of glacial AABW could have been much greater than today, even to the point that deep-ocean salinity stratification may have been reversed with respect to the modern26. Such salinity changes could be brought about by enhanced equatorward sea-ice export in the glacial SO28 in combination with reduced melting of Antarctic ice as a consequence of colder NADW20. Analyses of different boundary conditions in atmosphere–ocean general circulation model (AOGCM) equilibrium simulations suggest that especially the interplay of low CO2, low obliquity29 and large Northern Hemisphere ice sheets30 provides favourable conditions for the formation of salty deep waters around Antarctica.
Using the fully coupled Earth system model (COSMOS)29,31 (Methods), Zhang et al. have previously shown29 that the application of glacial boundary conditions can lead to particularly salty deep waters in the SO region compared with pre-industrial conditions. In this study, we augment the glacial (LGMCTRL) and pre-industrial (PIDCTRL) control experiments of Zhang et al.29 to include an intermediate climate state (40kaCTRL, Methods, Figs. 3 and 4 and Extended Data Figs. 2–9) to investigate any differences in the response to ‘terminal’ and non-terminal AMOC perturbations (which we describe later).
In the glacial ocean simulation LGMCTRL, the strongest temperature decrease (of more than 4 °C with respect to both PIDCTRL and 40kaCTRL) occurs within levels of the southward NADW return flow (Fig. 2 and Extended Data Figs. 2 and 3). The local LGMCTRL cooling maximum at ~2.5 km depth (Fig. 2c) can be linked to a combination of a shoaling (~200 m) of the glacial NADW cell and production of colder NADW (although we note that a model–data comparison for our glacial state with marine calcite δ18O values includes the possibility that NADW formation might actually have been weaker and even shallower32,33,34 than in our simulated LGM state35).
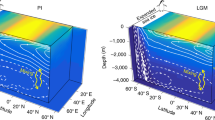
a,b, Interglacial (pre-industrial, PIDCTRL) (a) and glacial (Last Glacial Maximum, LGMCTRL) (b) temperature and salinity (practical salinity units (PSU), white contours) distribution. c,d, Glacial–interglacial difference (LGMCTRL – PIDCTRL) for temperature (c) and salinity (d). All fields represent 100 yr averages. Plotted using Ocean Data View (http://odv.awi.de).
In stark contrast to the changes at intermediate depths, the weakest temperature and strongest salinity differences between the pre-industrial and glacial states are detected in the deep SO (Fig. 2c,d). Here we observe a shift from a purely temperature-controlled stratification to one that is also characterized by a stable haline density gradient (at least within the SO). A similar contrast is observed between glacial and intermediate (40 thousand years ago (ka)) conditions (Extended Data Fig. 2).
We note that the mechanism of deep-ocean salinification proposed by Adkins20 (which calls on the cooling of NADW as a means for reducing the melting of Antarctic land ice and related input of freshwater to the SO) could work in tandem with increased sea-ice export (as observed in our model simulation) to produce highly saline bottom waters.
An overview of simulated salinity structure in LGM states (unperturbed) encompassing the last three Paleoclimate Model Intercomparison Project (PMIP)/Coupled Model Intercomparison Project (CMIP) model generations36,37,38,39,40 shows that a simulation of a salty glacial deep ocean (Extended Data Fig. 10) by AABW on a global scale is a persistent challenge, which partly reflects limits of current models to simulate key processes41,42 that influence AABW characteristics. This also includes the mechanism described by ref. 20, and while the current generation of coupled AOGCMs cannot resolve that mechanism explicitly, we can at least demonstrate its viability using a coupled ice-sheet/ice-shelf cavity model (Methods and Extended Data Fig. 4). However, the precise mechanism by which a salty deep ocean is generated is not important for the following discussion, in which we investigate the theoretical implications of a relative increase in the importance of salinity versus temperature stratification in the glacial ocean. For further discussion, see Methods.
Salinity gradient and temperature changes with depth
Deep-ocean stratification depends on the interplay between salinity and temperature changes with depth. We therefore derive an analytical expression (which is independent of the model simulations) for the thermal gradient (dT/dz) that accounts for the interplay between thermal and haline contributions to the net density change with depth:
Here, dρS/dz and dρT/dz represent the haline and thermally driven density changes with depth and dρ/dz is the combined (net) change in density with depth (which must remain positive to maintain stability). Density and the thermal expansion coefficient are indicated by ρ0 and αT. We now explore the implications of a glacial ocean state in which an increase in salinity stratification accommodates a decrease in the thermal contrast between northern- and southern-sourced deep-water masses. In particular, we are interested in the surface SO temperature response that would result from the upwelling of deeper waters (for example, due to a perturbation of the AMOC) that are relatively warm (not as cold) compared with a non-glacial state.
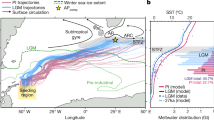
With the aid of the different terms in the equation, we can evaluate the importance of the stable glacial salinity stratification for the reduced thermal stratification in LGMCTRL. We focus our attention on the deep South Atlantic (zonally averaged at 30° S) to assess the export characteristics out of the Atlantic basin and to avoid effects of intra-basin scale upwelling on Southern Hemisphere communication. In particular, the choice of the depth level influences the thermohaline characteristics of the reference water masses. Therefore, we choose a level at 3,000 m depth, which is within a broader core of waters with similar stratification characteristics that represent an unstable (PIDCTRL, 40kaCTRL) or stable (LGMCTRL) salinity stratification. The first term on the right-hand side of the equation can then be diagnosed from our modelled control runs, enabling us to plot dT/dz versus the ratio of haline to thermally driven density changes (\(\frac{{{\mathrm{d}}\rho_{\mathrm{S}}/{\mathrm{d}}z}}{{{\mathrm{d}}\rho_{\mathrm{T}}/{\mathrm{d}}z}}\)) for a variety of background states (Fig. 3).
Temperature gradients (dT/dz) along lines of constant density stratification (dρ/dz) for the individual climate states with reference conditions from the zonally averaged Atlantic at 30° S and 3,000 m depth. The pressure reference level is 3,000 dbar to account for the impact of pressure conditions on temperature and stability properties at the chosen reference level of 3,000 m depth. The circles show the position of the simulated interglacial (PIDCTRL, black), 40 ka (40kaCTRL, green) and Last Glacial Maximum (LGMCTRL, blue) states (compare Extended Data Fig. 6). The curves show solutions for stable density stratification (dρ/dz > 0; that is, density increases with depth) with a stable thermal stratification (dρT/dz > 0; that is, temperature decreases with depth). Hence, positive values on the x axis indicate a stable haline stratification (dρS/dz > 0; that is, salinity increases with depth, pink shaded phase space) and negative values indicate an unstable haline stratification (dρS/dz < 0; that is, salinity decreases with depth, grey shaded phase space).
For any of the three different background states with a given density structure (dρ/dz, ρ0 and αT), it can be seen that for constant dρ/dz the ratio of haline to thermally driven density stratification must increase to accommodate any decrease in the vertical temperature contrast between northern- and southern-sourced deep-water components in the South Atlantic (coloured curves in Fig. 3). The key difference between our glacial simulation and a pre-industrial or intermediate (40 ka) state is the large increase in salinity stratification (which is actually reversed with respect to the non-LGM states) relative to the thermal stratification. Together with the palaeo-evidence described earlier, this suggests that the cooling potential of upwelled water to the surface SO in a full glacial is relatively much less than for either the pre-industrial or intermediate state. Naturally, this has implications for the oceanic and atmospheric response to a perturbation of the AMOC that might be expected as a necessary ingredient of glacial termination.
Southern high-latitude response to AMOC weakening
We next perform perturbation simulations to investigate the implications of different glacial–interglacial water-mass configurations with respect to SO and Antarctic temperature responses to an abrupt weakening of the AMOC (Fig. 4 and Extended Data Fig. 5). We use the same model set-up as in the control simulations and apply a freshwater perturbation of 0.15 Sv (1 Sv = 106 m3 s–1) to the North Atlantic ice-rafted debris belt for 800 years (further details are provided in Methods). In summary, we find that warming sea surface conditions and declining sea-ice cover occur as the dominant high-latitude Southern Hemisphere response to an AMOC weakening only under LGM conditions (Fig. 4d,e).
a, NADW export (Sv) at 30° S. b–d, Surface temperature (°C) and sea-ice area fraction changes (iso-lines) for interglacial (PIDPERT – PIDCTRL) (b), 40 ka (40kaPERT – 40kaCTRL) (c) and Last Glacial Maximum (LGMPERT – LGMCTRL) (d) conditions, averaged between model years 700 and 800. e, The averaged Antarctic surface temperature changes as a 100 yr running mean with the same colour code as in a. Panels b–d plotted using Ocean Data View (http://odv.awi.de).
In the following discussion, we focus on the comparison of the perturbation simulations LGMPERT and PIDPERT (the 40kaPERT responses are similar to those of PIDPERT) (Fig. 4). On weakening of AMOC, surface warming at the southern boundary of the Atlantic basin (~30° S) penetrates to a depth of ~2 km irrespective of the background conditions (Fig. 5a,b). This warming response is a common characteristic among NADW perturbation simulations43,44, which can be linked to heat storage45 in the low latitudes and South Atlantic and reduced ventilation of intermediate and deep waters, combined with the downward mixing of heat from the thermocline46. This ‘advection–diffusion balance’ concept is also consistent with the relatively strong LGMPERT warming (Fig. 5) along the perturbed glacial AMOC-return pathway (Extended Data Fig. 7), reflecting the more pronounced vertical temperature contrast across the NADW cell in the unperturbed LGMCTRL state (Fig. 2 and Extended Data Fig. 3).
a,b, Temperature anomalies by AMOC weakening for interglacial (PIDPERT − PIDCTRL) (a) and Last Glacial Maximum (LGMPERT − LGMCTRL) (b) conditions between model years 100 and 200 as a 100 yr mean, zonally averaged in the Atlantic sector. c, The difference between the glacial and interglacial anomalies (LGM − PID). Plotted using Ocean Data View (http://odv.awi.de).
In all experiments, the Atlantic basin temperature response below ~2 km is one of cooling (Fig. 5 and Extended Data Fig. 8) as the NADW cell weakens (Fig. 4a) and shoals (Extended Data Fig. 7) during the first ~200 years of hosing. Compared with PIDPERT, the more pronounced LGMPERT cooling between 2.0 and 2.5 km (Fig. 5c) reflects the initially shallower NADW cell (Extended Data Fig. 3) as the AMOC is perturbed (Extended Data Fig. 7). Below this depth, however, cooling in LGMPERT is weaker than in the PIDPERT (Fig. 5c). At first glance, this is perplexing since shoaling of the overturning cell (Extended Data Fig. 7) and isopycnals at these depth levels is more pronounced in LGMPERT (the density levels at 3,000 m depth in PIDCTRL and LGMCTRL shoal by ~160 m and ~230 m, not shown). However, the phenomenon is a direct consequence of the build-up of relatively warmer waters in the glacial deep ocean (with respect to intermediate depths) permitted by the increase in salt stratification (Fig. 3 and Extended Data Fig. 6).
As predicted, this fundamental change in deep-ocean stratification (from temperature controlled in PIDCTRL to one that is dependent on a stable haline density gradient in LGMCTRL) leads to a very different SO surface temperature response to North Atlantic freshwater forcing and AMOC perturbation. In PIDPERT, cooling is observed across the surface SO due to the upwelling of cold deep waters when the AMOC is in a perturbed state. By contrast, for LGMPERT between ~100 and 200 years we observe a continuous surface warming across Antarctic circumpolar latitudes south of ~45° S and extending into the Drake Passage (south of ~55° S), reflecting the upwelling of relatively warmer waters that characterize the glacial deep ocean in our simulations (Fig. 5 and Extended Data Figs. 8 and 9). It is important to emphasize that cooling does occur in the deep ocean during LGMPERT (Fig. 5b), but this cooling is reduced relative to PIDPERT (Fig. 5c) and, in combination with warming at intermediate depths, produces a net warming at the SO surface.
The contrasting SO surface temperature responses lead to very different temperature responses over Antarctica (Fig. 4e). In fact, the integrated surface heat flux anomaly south of 55° S is of opposite signs in LGMPERT and PIDPERT. Only in the glacial state does the AMOC perturbation result in atmospheric warming in the southernmost ocean region. When combined with atmospheric heat transport, the positive ocean–atmosphere heat flux observed in LGMPERT produces by far the largest and fastest temperature rise across Antarctica within the first ~200 years when compared with PIDPERT and 40kaPERT (Fig. 4e). After ~200–300 years, NADW strength and geometry have largely adjusted to the persistent freshwater perturbation, and Antarctic warming proceeds at a reduced rate.
Salty glacial deep ocean and deglaciation
We have demonstrated that a fundamental change in deep-ocean stratification can lead to a greatly enhanced climatic response to AMOC weakening while in a glacial state. The simulated Antarctic seesaw response is amplified by a factor of ~2 on a multicentennial timescale compared with interglacial or subglacial conditions. The surface cooling (as opposed to warming) that we observe in the SO high latitudes under pre-industrial and subglacial conditions might be a model-specific characteristic12, but it is important to note that the key to an amplified seesaw warming is a more pronounced haline to thermal density stratification ratio (which is predicted from proxy reconstructions, as described earlier). Increasing this ratio has the same effect irrespective of the climate background conditions, as shown in the phase space analysis in Fig. 3. The underlying mechanism might also therefore represent a key to understanding the spread of SO high-latitude responses in previous glacial AMOC perturbation experiments using a range of models47. For the specific model used in our study, a damped SO surface temperature response is obtained for LGM experiments using a modern-like salinity stratification29 as employed by Kageyama et al.47.
Our simulations do not include a representation of the global carbon cycle, but several previous studies have called on AMOC-induced stratification changes within the SO as a key player in glacial–interglacial CO2 variability48,49,50,51,52. Furthermore, it has also been suggested that AMOC-induced CO2 changes53 might provide an internal feedback with the potential to promote transitions between different climate states54. Abrupt changes in the mode of AMOC occurred throughout the last glacial period13 and were linked to temperature changes across Antarctica and (on occasion) variations in CO255, and yet only those changes associated with the last termination were sufficient to mark the transition back to an interglacial state. Previous studies have suggested various combinations of ice-sheet size2 and specific orbital configurations1,56 in an attempt to explain why glacial termination occurs only when it does. Our findings provide an alternative explanation: that global-scale water-mass salinity characteristics represent a key player to promote deglaciation once a salty deep-ocean reservoir has been formed at full glacial conditions.
Methods
Rate of change in Antarctic temperature records
In Fig. 1, the relatively large rates of change observed in the upper sections of the record (particularly the Holocene, which has not experienced high-amplitude millennial-scale variability) using a 200 yr pre-smooth reflects the much higher temporal resolution of the upper sections of ice cores relative to deeper sections. Using a pre-smoothing of 500 yr alleviates this problem while (in our opinion) preserving an accurate (not overly smoothed) representation of the relative rates of change associated with millennial-scale events.
Model description
We use the comprehensive fully coupled Earth system model COSMOS (ECHAM5-JSBACH-MPIOM) in this study. The atmospheric model ECHAM558, complemented by a land surface component with dynamic vegetation JSBACH59, is used at T31 resolution (~3.75°), with 19 vertical hybrid sigma-pressure levels. The ocean model MPIOM60, including sea-ice dynamics that are formulated using viscous-plastic rheology61, runs on a bipolar curvilinear Arakawa-C grid. The grid size (120 × 101) corresponds to a formal longitudinal resolution of ~3° (360/120) and a latitudinal resolution of ~1.8° (180/101). The vertical domain is represented by 40 unevenly spaced depth layers. The climate model has already been used to simulate, for example, the past millennium31, the Miocene warm climate62,63, the Pliocene64, the internal variability of the climate system65, the Last Glacial Maximum climate29,47 and glacial millennial-scale variability at intermediate climate conditions54,66. The glacial (LGMCTRL) and pre-industrial (PIDCTRL) states used in our study are experiments LGMW and PI from Zhang et al.29. The glacial state is characterized by a salty deep-ocean reservoir in reasonable agreement with available salinity reconstructions. Note that the generation of an interglacial-to-glacial salinity reversal is expected to be dependent on, for example, the model itself, the model configuration and the experimental set-up (Extended Data Fig. 10). However, for the mechanism described here, a salinity reversal per se is not necessary. The data-based demand that the temperature gradient between northern and southern sources of deep water within the Atlantic was reduced during the LGM compared with today20 implies that a reduction in the thermal deep-ocean stratification was accompanied by a stronger glacial salinity increase of AABW relative to NADW. Were this not the case, then the density stratification of the glacial South Atlantic/SO would necessarily have been weaker than today. A simple evaluation for the importance of a glacial salinity reversal for glacial–interglacial density changes is provided in the corresponding section.
Experimental design
Besides the pre-industrial (PIDCTRL) and the Last Glacial Maximum (LGMCTRL) control climates from Zhang et al.29, we conduct an equilibrated MIS3 control simulation (40kaCTRL) by imposing fixed boundary conditions for 40 ka. In detail, the three orbital parameters in experiment 40kaCTRL are 0.013146 (eccentricity), 358.17° (precession of the equinoxes, the angle between the Earth’s position during the Northern Hemisphere vernal equinox and the orbit perihelion) and 23.61° (obliquity)67. The greenhouse gas concentrations are 195 ppm (CO2), 413 ppb (CH4) and 231 ppb (N2O)68,69. The ice-sheet configuration is a combination of ice-sheet reconstructions from ICE-5G70 and PMIP3. That is, the topography anomaly between 40 ka and the LGM in ICE-5G is first calculated and then is added to the PMIP3 LGM topography29. Global mean sea level is ~80 m lower at 40 ka than the pre-industrial level. Experiment 40kaCTRL is integrated for 5,000 years to an equilibrated state that serves as the starting point for the perturbation experiment.
Identical hosing experiments are then conducted under the three different climate backgrounds in experiments PIDPERT, LGMPERT and 40kaPERT. A freshwater flux of 0.15 Sv is added to the Ruddiman Belt (40°–55° N, 45°–20° W) for 800 years to ensure a quasi-equilibrated response in the SO. A freshwater perturbation of 0.15 Sv agrees with estimates of deglacial meltwater release during Heinrich Stadial 1 as assessed in different studies71,72,73. Global mean sea-level height is corrected for the input of additional freshwater. Hence, coastlines remain the same during a freshwater perturbation experiment. Averages of 100 years are shown in our results.
Vertical temperature and salinity changes
On the basis of the linear approximation of the density equation and neglected pressure variations, we can calculate density changes with depth by:
where ρ0 is density, T is temperature, S is salinity, αT is the thermal expansion coefficient and βS is the haline contraction coefficient. So that a temperature contribution to density changes with depth equates to:
and a salinity contribution equates to:
Rearrangement of equation (2) leads to:
Further substituting dρT/dz in equation (4) by:
temperature changes with depth can be expressed as a function of the ratio between the haline and thermal density changes with depth:
Formation of a salty glacial deep ocean: model limitations
State-of-the-art AOGCMs lack fully interactive ice-sheet components and do not allow to simulate increased glacial melt in response to ocean warming. Furthermore, essential processes such as ice shelf–ice cavity ocean interactions are not included in the current generation of fully coupled AOGCMs74, which limits the ability to investigate a fuller spectrum of relevant processes and interactions such as the ‘pre-freshening’20 of AABW via NADW. Furthermore, the ocean model component in our study and other global climate models is too coarse to represent the northward transport of dense shelf waters across the Antarctic shelf edge and their subsequent sinking to depth74, which represents a fundamental source of abyssal ocean circulation in the modern ocean. However, there is another mode associated with open-ocean convection75 that has been identified as an additional surface to deep-ocean exchange process based on satellite data76,77. This modern mode with notable deep (>2,000 m) open-ocean convection between 90° S and 55° S under pre-industrial conditions has been diagnosed in more than two-thirds of the CMIP5 models. While this polynya-induced mode is not dominant today, it could have been the main source of AABW formation during full glacial conditions with a widely ice-covered continental shelf and a lower sea level than today. This situation might have favoured a glacial open-ocean type convection mode that is free to reach the seafloor75.
In that sense, a dominant glacial production regime of AABW by open-ocean convection, predominantly in the centres of the Weddell and Ross Sea gyres, as modelled in our model set-up78 might capture the actual glacial water-mass conversion much better than under modern conditions.
To test the viability of the mechanism for the generation of a salty glacial deep ocean as proposed by Adkins20, we have evaluated how far our simulated control states are consistent with less melting of Antarctic ice by colder NADW during glacial conditions. In this context, we have applied the Potsdam Ice-Shelf Cavity Model (PICO)79 to quantify changes in the subshelf melt rates. PICO is developed from the ocean box model of Olbers and Hellmer80 and is implemented as a module of the Parallel Ice Sheet Model (PISM)81 to simulate the vertical overturning circulation in ice-shelf cavities and thus enables the computation of subshelf melt rates (Extended Data Fig. 4) consistent with this circulation. We run the simulations at a spatial resolution of 16 × 16 km. The PICO settings are the standard settings that were used by Reese et al.79 to obtain a realistic pre-industrial ice sheet. The PISM settings were taken from Sutter et al.82, and the atmospheric forcing is from regridded yearly RACMO2.3 2 m air temperature and precipitation fields83.
Driving this model set-up with the thermohaline ocean fields of experiment PIDCTRL in equilibrium simulations of 200 kyr we end up with an aggregated melt flux of ~1,400 Gt yr−1 (Extended Data Fig. 4a), which is not far from the observed value 1,500 ± 237 Gt yr−1 for present-day conditions84. Keeping the same experimental set-up but replacing the thermohaline fields by the 40kaCTRL and LGMCTRL fields, results in a reduction of the aggregated melt flux by ~26% and 50%, respectively. This suggests that a reduction of Antarctic ice melt by colder NADW could indeed contribute to the generation and maintenance of a salty deep-ocean reservoir, especially since surface melt rates are negligible in the contribution to Antarctic ice-mass loss for modern climate conditions and colder climates. Hence, attempts should be made to incorporate this mechanism in future Earth system model approaches to explore essential interactions in particular at the ice–ocean interface, and it is open to question how far a fuller representation of the AABW formation mechanism would lead to a different model response. These investigations should be combined with the analysis of, for example, benthic foraminiferal δ18O and Mg/Ca records to discriminate sea-ice-derived versus Antarctic-ice-derived salinity stratification.
Glacial deep-ocean salinity structure in models of different PMIP/CMIP generations
Currently, there is no collective framework of perturbation experiments for glacial and interglacial conditions that would allow us to test our perturbation experiments within a model intercomparison. Nevertheless, we have generated an overview of simulated glacial deep-ocean salinity structure in LGM states (unperturbed) encompassing the last three PMIP/CMIP model generations (Extended Data Fig. 10).
Using the same model as employed in our study, the glacial deep-ocean salinity structure (including a PMIP2/CMIP436,37 model intercomparison) was investigated in the study of Zhang et al.29. From the six other models in that study, two models (CCSM385 and HadCM3M286) also generated a stable glacial salt stratification (Extended Data Fig. 10). Note that PMIP utilized no specific protocol concerning the initial ocean condition for LGM simulations36,37, and notably the three models (including COSMOS) that were initialized from a previous glacial ocean state were the only ones to simulate a stable glacial deep-ocean salt stratification29. We suggest that this difference is a key to the different outcomes.
In model simulations at hand for the PMIP3/CMIP538,39 and PMIP4/CMIP640 generations, the north–south deep-ocean salinity contrast is dominated by a relatively salty North Atlantic, except within CCSM487. In that model, saltier deep SO conditions are simulated, but these salinity characteristics do not extend into the Atlantic basin. Hence, the simulation of a salty glacial deep ocean via AABW at a global scale is not a coherent characteristic in LGM simulations with current coupled AOGCMs.
Where do we stand now? We think at least three possibilities should be taken into account for further research:
-
The inference of a salinity-stratified glacial ocean via AABW has been questioned, and the scarce pore-water chlorinity data availability necessitates an increase in data constraints88.
-
The simulation of a salty deep ocean seems to depend on conditions before the LGM, which therefore need to be incorporated into transient simulations rather than initiating models with LGM boundary conditions29. In particular, orbital configurations incorporating low obliquity and low atmospheric CO2 concentrations in combination with Northern Hemisphere ice sheets in a later stage of a glacial cycle (but before the glacial maxima) should be considered as an alternative framework for simulating a salty glacial deep ocean29,30.
-
Models need to be improved; accurate formation of AABW via shelf processes is an ongoing challenge41. Furthermore, important processes such as interactive ice sheets and shelf–ice cavity ocean interactions need to be included for detailed studies, and we note that the mechanism of deep-ocean salinification proposed by Adkins20 (Extended Data Fig. 4) could work in tandem with increased sea-ice export to produce highly saline bottom waters. Recently, it has also been suggested that the export of icebergs from the SO to the Atlantic basin might modify interglacial-to-glacial salt balance between NADW and AABW42. As yet, these key processes and mechanisms are missing in coupled climate models, and therefore the conjecture that models that are simulating the salty reservoir might do it for the wrong reason cannot be excluded.
Glacial deep-ocean salinity constraints
The observation/reconstruction of extremely high glacial SO salinities and abyssal waters is very scarce, and a salinity value of 37.1 ± 0.2 PSU at Shona Rise26 represents a singularity that has been questioned by the analyses of pore fluid chlorinity/salinity data from deep-sea cores using estimation methods deriving from linear control theory88. Similarly to the ‘glacial’ state in Galbraith and Lavergene30, we simulate a lower salinity at this core location (36.04 PSU). Aside from this extreme salinity value, our simulated salinity in the deep Pacific between 3,500 m and 5,500 m is 36.03. This value is within the uncertainty of the reconstructed salinity (36.1 ± 0.1) based on chloride concentrations of deep Pacific bottom waters at five different core locations containing the same depth range27.
Estimates for the importance of salinity changes
To estimate the importance of interglacial-to-glacial salinity changes for the maintenance of deep-ocean stratification, we suggest two simple criteria. One criterion can help to evaluate the necessity of salinity changes in the evolution of the simulated glacial temperature structure. For example, in the PIDCTRL and LGMCTRL experiment pair (Fig. 2), an unstable glacial situation applies if:
That is, the glacial temperature decrease with depth is too weak to balance the effect of pre-industrial salinity decrease with depth on density (compare Extended Data Fig. 1).
While the latter criterion can help to assess the necessity of salinity changes, it does not answer the importance of a salinity reversal and the transition from an unstable to a stable salinity structure. Therefore, we additionally suggest to compare the LGMCTRL with a PIDCTRL temperature gradient that would result from the shift of the unstable to a neutral salt stratification. This can be depicted in Fig. 3. Here the glacial cooling with depth (blue dot) is weaker than the intercept of the PIDCTRL solution with the y axis. The corresponding criterion can be expressed as:
That is, even if the unstable haline stratification contribution to dρ_PID/dz would be replaced by a neutral haline density stratification (dρS_PID/dz = 0), the reduced thermal stratification along solutions with constant dρ_PID/dz, αT_PID and ρ0_PID still requires a cooling with depth, which is stronger than dT_LGM/dz.
Data availability
The ice-core data used in this paper are available via the referenced sources. The results from the PMIP3–CMIP5 and PMIP4–CMIP6 models can be found on the ESGF (Earth System Grid Federation) website. The PMIP2 Data Archive is available via http://pmip2.lsce.ipsl.fr/. Ice-sheet model data of this study are available at Pangaea (https://doi.org/10.1594/PANGAEA.927126). COSMOS model data that provide the basis for figures are archived on Zenodo (https://doi.org/10.5281/zenodo.5137637).
Code availability
The standard model code of the comprehensive fully coupled atmosphere–ocean general circulation model (AOGCM), COSMOS (version COSMOS-landveg r2413, 2009) is available upon request from the Max Planck Institute for Meteorology in Hamburg (https://www.mpimet.mpg.de). Post-processing of model output and model data analysis has been performed with CDO (Climate Data Operators, versions 1.7.1, 1.9.5 and 1.9.10, https://code.mpimet.mpg.de/projects/cdo). We thank the developers of PISM and PICO for making their code publicly available at https://github.com/pism/pism/tree/v1.1-1-gb8b99b3.
References
Imbrie, J. et al. On the structure and origin of major glaciation cycles 2. The 100,000‐year cycle. Paleoceanography 8, 699–735 (1993).
Raymo, M. E. The timing of major climate terminations. Paleoceanography 12, 577–585 (1997).
Milankovitch, M. Kanon der Erdbestrahlung und seine Andwendung auf das Eiszeitenproblem (Royal Serbian Academy, 1941).
Hays, J. D., Imbrie, J. & Shackleton, N. J. Variations in the Earth’s orbit: pacemaker of the Ice Ages. Science 194, 1121–1132 (1976).
Denton, G. H. et al. The last glacial termination. Science 328, 1652–1656 (2010).
Wolff, E. W., Fischer, H. & Röthlisberger, R. Glacial terminations as southern warmings without northern control. Nat. Geosci. 2, 206–209 (2009).
Barker, S. et al. Interhemispheric Atlantic seesaw response during the last deglaciation. Nature 457, 1097–1102 (2009).
Broecker, W. S. Paleocean circulation during the last deglaciation: a bipolar seesaw? Paleoceanography 13, 119–121 (1998).
Stocker, T. F. & Johnsen, S. J. A minimum thermodynamic model for the bipolar seesaw. Paleoceanography 18, 1087 (2003).
Crowley, T. J. North Atlantic Deep Water cools the Southern Hemisphere. Paleoceanography 7, 489–497 (1992).
Ganopolski, A. & Rahmstorf, S. Rapid changes of glacial climate simulated in a coupled climate model. Nature 409, 153–158 (2001).
Stouffer, R. J. et al. Investigating the causes of the response of the thermohaline circulation to past and future climate changes. J. Clim. 19, 1365–1387 (2006).
Henry, L. et al. North Atlantic Ocean circulation and abrupt climate change during the last glaciation. Science 353, 470–474 (2016).
Cheng, H. et al. The Asian monsoon over the past 640,000 years and ice age terminations. Nature 534, 640–646 (2016).
Toggweiler, J. R. & Samuels, B. Effect of Drake Passage on the global thermohaline circulation. Deep Sea Res. 42, 477–500 (1995).
Marshall, J. & Speer, K. Closure of the meridional overturning circulation through Southern Ocean upwelling. Nat. Geosci. 5, 171–180 (2012).
Gnanadesikan, A. A simple predictive model for the structure of the oceanic pycnocline. Science 283, 2077–2079 (1999).
Talley, L. D. Closure of the global overturning circulation through the Indian, Pacific, and Southern Oceans: schematics and transports. Oceanography 26, 80–97 (2013).
Orsi, A. H., Smethie, W. M. & Bullister, J. L. On the total input of Antarctic waters to the deep ocean: a preliminary estimate from chlorofluorocarbon measurements. J. Geophys. Res. 107, 31-1–31-14 (2002).
Adkins, J. F. The role of deep ocean circulation in setting glacial climates. Paleoceanography 28, 539–561 (2013).
Bereiter, B. et al. Mean global ocean temperatures during the last glacial transition. Nature 553, 39–44 (2018).
Johnson, G. C. Quantifying Antarctic Bottom Water and North Atlantic Deep Water volumes. J. Geophys. Res. 113, C05027 (2008).
Roberts, J. et al. Evolution of South Atlantic density and chemical stratification across the last deglaciation. Proc. Natl Acad. Sci. USA 113, 514–519 (2016).
Curry, W. B. & Oppo, D. W. Glacial water mass geometry and the distribution of δ13C of ∑CO2 in the western Atlantic Ocean. Paleoceanography 20, PA1017 (2005).
Howe, J. N. W. & Piotrowski, A. M. Atlantic deep water provenance decoupled from atmospheric CO2 concentration during the lukewarm interglacials. Nat. Commun. 8, 2003 (2017).
Adkins, J. F., McIntyre, K. & Schrag, D. P. The salinity, temperature and δ18O content of the glacial deep ocean. Science 298, 1769–1773 (2002).
Insua, T. L., Spivack, A. J., Graham, D., D’ Hondt, S. & Moran, K. Reconstruction of Pacific Ocean bottom water salinity during the Last Glacial Maximum. Geophys. Res. Lett. 41, 2914–2920 (2014).
Shin, S. I., Liu, Z. G., Otto-Bliesner, B. L., Kutzbach, J. E. & Vavrus, S. J. Southern Ocean sea-ice control of the glacial North Atlantic thermohaline circulation. Geophys. Res. Lett. 30, 1096 (2003).
Zhang, X., Lohmann, G., Knorr, G. & Xu, X. Different ocean states and transient characteristics in Last Glacial Maximum simulations and implications for deglaciation. Clim. Past 9, 2319–2333 (2013).
Galbraith, E. D. & de Lavergne, C. Response of a comprehensive climate model to a broad range of external forcings: relevance for deep ocean ventilation and the development of late Cenozoic ice ages. Clim. Dyn. 52, 653–679 (2019).
Jungclaus, J. H. et al. Climate and carbon-cycle variability over the last millennium. Clim. Past. 6, 723–737 (2010).
Böhm, E. et al. Strong and deep Atlantic meridional overturning circulation during the last glacial cycle. Nature 517, 73–76 (2015).
Lynch-Stieglitz, J. The Atlantic meridional overturning circulation and abrupt climate change. Annu. Rev. Mar. Sci. 9, 83–104 (2017).
Skinner, L. et al. Radiocarbon constraints on the glacial ocean circulation and its impact on atmospheric CO2. Nat. Commun. 8, 16010 (2017).
Werner, M. et al. Glacial–interglacial changes in H218O, HDO and deuterium excess—results from the fully coupled ECHAM5/MPI-OM Earth system model. Geosci. Model Dev. 9, 647–670 (2016).
Braconnot, P. et al. Results of PMIP2 coupled simulations of the mid-Holocene and Last Glacial Maximum—part 1: experiments and large-scale features. Clim. Past 3, 261–277 (2007).
Weber, S. et al. The modern and glacial overturning circulation in the Atlantic Ocean in PMIP coupled model simulations. Clim. Past 3, 51–64 (2007).
Braconnot, P. et al. Evaluation of climate models using palaeoclimatic data. Nat. Clim. Change 2, 417–424 (2012).
Braconnot, P. et al. The Paleoclimate Modeling Intercomparison Project contribution to CMIP5. CLIVAR Exch. 16, 15–19 (2011).
Kageyama, M. et al. The PMIP4 contribution to CMIP6—part 4: scientific objectives and experimental design of the PMIP4-CMIP6 Last Glacial Maximum experiments and PMIP4 sensitivity experiments. Geosci. Model Dev. 10, 4035–4055 (2017).
Heuzé, C. Antarctic Bottom Water and North Atlantic Deep Water in CMIP6 models. Ocean Sci. 17, 59–90 (2021).
Starr, A. et al. Antarctic icebergs reorganize ocean circulation during Pleistocene glacials. Nature 589, 236–241 (2021).
Galbraith, E. D., Merlis, T. M., & Palter, J. B. Destabilization of glacial climate by the radiative impact of Atlantic meridional overturning circulation disruptions. Geophys. Res. Lett. 43, 8214–8221 (2016).
Pedro, J. B. et al. Beyond the bipolar seesaw: toward a process understanding of interhemispheric coupling. Quat. Sci. Rev. 192, 27–46 (2018).
Stommel, H. Thermohaline convection with two stable regimes of flow. Tellus 13, 224–230 (1961).
Rühlemann, C. et al. Intermediate depth warming in the tropical Atlantic related to weakened thermohaline circulation: combining paleoclimate data and modeling results for the last deglaciation. Paleoceanography 19, PA1025 (2004).
Kageyama, M. et al. Climatic impacts of fresh water hosing under Last Glacial Maximum conditions: a multi-model study. Clim. Past 9, 935–953 (2013).
Sigman, D. M. & Boyle, E. A. Glacial/interglacial variations in atmospheric carbon dioxide. Nature 407, 859–869 (2000).
Anderson, R. F. et al. Wind-driven upwelling in the Southern Ocean and the deglacial rise in atmospheric CO2. Science 323, 1443–1448 (2009).
Skinner, L. C., Fallon, S., Waelbroeck, C., Michel, E. & Barker, S. Ventilation of the deep Southern Ocean and deglacial CO2 rise. Science 328, 1147–1151 (2010).
Ferrari, R. et al. Antarctic sea ice control on ocean circulation in present and glacial climates. Proc. Natl Acad. Sci. USA 111, 8753–8758 (2014).
Watson, A. J., Vallis, G. K. & Maxim Nikurashin, M. Southern Ocean buoyancy forcing of ocean ventilation and glacial atmospheric CO2. Nat. Geosci. 8, 861–864 (2015).
Schmittner, A. & Galbraith, E. D. Glacial greenhouse-gas fluctuations controlled by ocean circulation changes. Nature 456, 373–376 (2008).
Zhang, X., Knorr, G., Lohmann, G. & Barker, S. Abrupt North Atlantic circulation changes in response to gradual CO2 forcing in a glacial climate state. Nat. Geosci. 10, 518–523 (2017).
Ahn, J. & Brook, E. J. Atmospheric CO2 and climate on millennial time scales during the last glacial period. Science 83, 83–85 (2008).
Tzedakis, P., Crucifix, M., Mitsui, T. & Wolff, E. W. A simple rule to determine which insolation cycles lead to interglacials. Nature 542, 427–432 (2017).
Parrenin, F. et al. Synchronous change of atmospheric CO2 and Antarctic temperature during the last deglacial warming. Science 339, 1060–1063 (2013).
Roeckner, E. et al. The Atmospheric General Circulation Model ECHAM5 Part 1: Model Description Report No. 349 (Max Planck Institute for Meteorology, 2003).
Brovkin, V., Raddatz, T., Reick, C. H., Claussen, M. & Gayler, V. Global biogeophysical interactions between forest and climate. Geophys. Res. Lett. 36, L07405 (2009).
Marsland, S. J., Haak, H., Jungclaus, J. H., Latif, M. & Röske, F. The Max-Planck-Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Model. 5, 91–127 (2003).
Hibler, W. III A dynamic thermodynamic sea ice model. J. Phys. Oceanogr. 9, 815–846 (1979).
Knorr, G. & Lohmann, G. Climate warming during Antarctic ice sheet expansion at the Middle Miocene transition. Nat. Geosci. 7, 376–381 (2014).
Knorr, G., Butzin, M., Micheels, A. & Lohmann, G. A warm Miocene climate at low atmospheric CO2 levels. Geophys. Res. Lett. 38, L20701 (2011).
Stepanek, C., Samakinwa, E., Knorr, G. & Lohmann, G. Contribution of the coupled atmosphere–ocean–sea ice–vegetation model COSMOS to the PlioMIP2. Clim. Past 16, 2275–2323 (2020).
Wei, W., Lohmann, G. & Dima, M. Distinct modes of internal variability in the global meridional overturning circulation associated with the Southern Hemisphere westerly winds. J. Phys. Oceanogr. 42, 785–80 (2012).
Zhang, X., Lohmann, G., Knorr, G. & Purcell, C. Abrupt glacial climate shifts controlled by ice sheet changes. Nature 512, 290–294 (2014).
Berger, A. Long-term variations of caloric insolation from the Earth’s orbital elements. Quat. Res. 9, 139–167 (1978).
Ahn, J. & Brook, E. J. Siple Dome ice reveals two modes of millennial CO2 change during the last ice age. Nat. Commun. 5, 3723 (2014).
Köhler, P., Nehrbass-Ahles, C., Schmitt, J., Stocker, T. F. & Fischer, H. A 156 kyr smoothed history of the atmospheric greenhouse gases CO2, CH4, and N2O and their radiative forcing. Earth Syst. Sci. Data 9, 363–387 (2017).
Peltier, W. R. Global glacial isostasy and the surface of the ice-age Earth: the ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet Sci. 32, 111–149 (2004).
Dowdeswell, I. N. et al. Iceberg production, debris rafting, and the extent and thickness of Heinrich layers (H-1, H-2) in North Atlantic sediments. Geology 23, 301–304 (1995).
Hemming, S. R. Heinrich events: massive late Pleistocene detritus layers of the North Atlantic and their global climate imprint. Rev. Geophys. 42, RG1005 (2004).
Clark, P. et al. Consequences of twenty-first-century policy for multi-millennial climate and sea-level change. Nat. Clim. Change 6, 360–369 (2016).
Lavergne, C., Palter, J. B., Galbraith, E. D., Bernardello, R. & Marinov, I. Cessation of deep convection in the open Southern Ocean under anthropogenic climate change. Nat. Clim. Change 4, 278–282 (2014).
Gordon, A. L. Oceanography: Southern Ocean polynya. Nat. Clim. Change 4, 249–250 (2014).
Zwally, H. J. & Gloersen, P. Passive microwave images of the polar regions and research applications. Polar Rec. 18, 431–450 (1977).
Carsey, F. D. Microwave observation of the Weddell Polynya. Mon. Weather Rev. 108, 2032–2044 (1980).
Abelmann, A. et al. The seasonal sea-ice zone in the glacial Southern Ocean as a carbon sink. Nat. Commun. 6, 8136 (2015).
Reese, R., Albrecht, T., Mengel, M., Asay-Davis, X. & Winkelmann, R. Antarctic sub-shelf melt rates via PICO. Cryosphere 12, 1969–1985 (2018).
Olbers, D. & Hellmer, H. A box model of circulation and melting in ice shelf caverns. Ocean Dynam. 60, 141–153 (2010).
Bueler, E. & Brown, J. Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model. J. Geophys. Res. 114, F03008 (2009).
Sutter, J. et al. Modelling the Antarctic ice sheet across the mid-Pleistocene transition – implications for oldest ice. Cryosphere 13, 2023–2041 (2019).
van Wessem, J. M. et al. Improved representation of East Antarctic surface mass balance in a regional atmospheric climate model. J. Glaciol. 60, 761–770 (2014).
Rignot, E., Jacobs, S., Mouginot, J. & Scheuchl, B. Ice-shelf melting around Antarctica. Science 341, 266–270 (2013).
Otto-Bliesner, B. et al. Last Glacial Maximum ocean thermohaline circulation: PMIP2 model intercomparisons and data constraints. Geophys. Res. Lett. 34, L12706 (2007).
Gordon, C. et al. The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim. Dyn. 16, 147–168 (2000).
Brady, E. C., Otto-Bliesner, B. L., Kay, J. E. & Rosenbloom, N. Sensitivity to glacial forcing in the CCSM4. J. Clim. 26, 1901–1925 (2013).
Wunsch, C. Pore fluids and the LGM ocean salinity—reconsidered. Quat. Sci. Rev. 135, 154–170 (2016).
K-1 Model developers K-1 Coupled GCM (MIROC) Description (eds Hasumi, H. & Emori, S.) (Center for Climate System Research, Univ. of Tokyo, 2004).
de Vries, P. & Weber, S. L. The Atlantic freshwater budget as a diagnostic for the existence of a stable shut down of the meridional overturning circulation. Geophys. Res. Lett. https://doi.org/10.1029/2004GL021450 (2005).
Marti, O. et al. The New IPSL Climate System Model: IPSL-CM4 (Institut Pierre Simon Laplace, 2005).
Yu, Y., Zhang, X. & Guo, Y. Global coupled ocean–atmosphere general circulation models in LASG/IAP. Adv. Atmos. Sci. 21, 444–455 (2004).
Voldoire, A. et al. The CNRM-CM5.1 global climate model: description and basic evaluation. Clim. Dyn. 40, 2091–2121 (2013).
Zheng, W. & Yu, Y. Paleoclimate simulations of the mid-Holocene and last glacial maximum by FGOALS. Adv. Atmos. Sci. 30, 684–698 (2013).
Ullman, D. J., LeGrande, A. N., Carlson, A. E., Anslow, F. S. & Licciardi, J. M. Assessing the impact of Laurentide Ice Sheet topography on glacial climate. Clim. Past 10, 487–507 (2014).
Sueyoshi, T. et al. Set-up of the PMIP3 paleoclimate experiments conducted using an Earth system model, MIROC-ESM. Geosci. Model Dev. 6, 819–836 (2013).
Dufresne, J. L. et al. Climate change projections using the IPSL-CM5 Earth system model: from CMIP3 to CMIP5. Clim. Dyn. 40, 2123–2165 (2013).
Adloff, M., Reick, C. H. & Claussen, M. Earth system model simulations show different feedback strengths of the terrestrial carbon cycle under glacial and interglacial conditions. Earth Syst. Dyn. 9, 413–425 (2018).
Yukimoto, S. et al. A new global climate model of the Meteorological Research Institute: MRI‐CGCM3‐model description and basic performance. J. Meteorol. Soc. Jpn. 90A, 23–64 (2012).
Lohmann, G., Butzin, M., Eissner, N., Shi, X. & Stepanek, C. Abrupt climate and weather changes across timescales. Paleoceanogr. Paleoclimatol. 35, e2019PA003782 (2020).
Shi, X., Hu, Y., Danek, C., Lohmann, G. AWI AWI-ESM1.1LR Model Output Prepared for CMIP6 PMIP lgm (Earth System Grid Federation, 2020); https://doi.org/10.22033/ESGF/CMIP6.9330
Sidorenko, D. et al. Evaluation of FESOM2.0 coupled to ECHAM6.3: pre-industrial and HighResMIP simulations. J. Adv. Model. Earth Syst. https://doi.org/10.1029/2019MS001696 (2019).
Hajima, T. et al. Development of the MIROC-ES2L Earth system model and the evaluation of biogeochemical processes and feedbacks. Geosci. Model Dev. 13, 2197–2244 (2020).
Ohgaito, R. et al. MIROC MIROC-ES2L Model Output Prepared for CMIP6 PMIP lgm (Earth System Grid Federation, 2019); https://doi.org/10.22033/ESGF/CMIP6.5644
Mauritsen, T. et al. Developments in the MPI-M Earth system model version 1.2 (MPI-ESM1.2) and its response to increasing CO2. J. Adv. Model. Earth Syst. 11, 998–1038 (2019).
Jungclaus, J. et al. MPI-M MPI-ESM1.2-LR Model Output Prepared for CMIP6 PMIP lgm (Earth System Grid Federation, 2019); https://doi.org/10.22033/ESGF/CMIP6.6642
Acknowledgements
We thank colleagues in the Paleoclimate Dynamics group at the Alfred Wegener Institute Helmholtz Center for Polar and Marine Research (AWI) in Bremerhaven for general support and the AWI Computing Centre for keeping the supercomputer running. M. Fahrenberg is acknowledged for downloading PMIP4 data, and we thank X. Shi for providing LGM salinity data for AWI-ESM. We acknowledge financial support by PACES and REKLIM through the Helmholtz association, as well as from PalMod (01LP1504A and 01LP1915A) through the German Federal Ministry of Education and Research to G.K. We also acknowledge financial support from the National Science Foundation of China (41988101 and 42075047) to X.Z. and UK NERC (grants NE/J008133/1 and NE/L006405/1) to S.B. Development of PISM is supported by NSF grants PLR-1603799 and PLR-1644277 and NASA grant NNX17AG65G. Computational resources were made available by the infrastructure and support of the computing centre of the Alfred Wegener Institute in Bremerhaven and the DKRZ in Hamburg, Germany. The authors also thank all the modelling groups who provided the PMIP2, PMIP3 and PMIP4 output for analysis, WCRP, CMIP panel, PCMDI, ESGF infrastructures for sharing data, WCRP and CLIVAR for supporting the PMIP project. The Laboratoire des Sciences du Climat et de l’Environnement (LSCE) is acknowledged for collecting and archiving the PMIP2 model data. The PMIP2 Data Archive is supported by CEA, CNRS and the Programme National d’Etude de la Dynamique du Climat (PNEDC).
Funding
Open access funding provided by Alfred-Wegener-Institute, Helmholtz Centre for Polar and Marine Research.
Author information
Authors and Affiliations
Contributions
G.K. conceived and developed the research. X.Z. designed and performed the COSMOS experiments. L.B.S. performed the ice-sheet model simulations. G.K. wrote the manuscript with help from S.B. All authors contributed to the interpretation and discussion of the results and to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Geoscience thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: James Super.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Simulated density changes with depth for pre-industrial conditions and a hybrid state of Last Glacial Maximum temperature and pre-industrial salinity conditions averaged in the Atlantic sector.
Shown are potential density (σ3) changes with depth (in kg m−4) for a) preindustrial conditions and b) a pseudo-modern state that combines simulated temperature and salinity fields for glacial and pre-industrial conditions, respectively. For the preindustrial state positive values indicate a stable stratification in the whole domain of panel a). In contrast, the zero-contour line in panel b) indicates that an unstable stratification (negative values) would arise for such a pseudo-hybrid state in large parts of the deep Atlantic below depths of ~2800 m. Simulated glacial and pre-industrial temperature and salinity fields are shown in Fig. 2.
Extended Data Fig. 2 Simulated 40ka temperature and salinity distribution and the Last Glacial Maximum anomalies to this state as zonal averages in the Atlantic sector.
Temperature (°C) and salinity (PSU, white contours) distribution for a) intermediate climate conditions (40kaCTRL). Panels b) and c) show the glacial - 40ka difference (LGMCTRL – 40kaCTRL) for temperature and salinity, respectively. All fields represent 100-year averages.
Extended Data Fig. 3 Simulated Atlantic overturning stream-function for different climate conditions and the differences between the glacial state and the interglacial and intermediate climate states.
Atlantic overturning stream-functions (Sv, 106 m3 s−1) for a) interglacial (PIDCTRL), b) intermediate (40kaCTRL) and c) glacial (LGMCTRL) climate conditions, as well as the differences d) between glacial and interglacial conditions (LGMCTRL - PIDCTRL) and e) between glacial and intermediate climate conditions (LGMCTRL – 40kaCTRL). Shown are 100 year averages. Solid contours indicate clockwise NADW circulation and doted contours anti-clockwise AABW circulation.
Extended Data Fig. 4 Simulated basal melt rates for different thermo-haline conditions.
Basal melt rates as simulated using PISM-PICO for a) interglacial (PIDCTRL), b) intermediate (40kaCTRL) and c) glacial (LGMCTRL) climate conditions. All simulations are identical except the thermo-haline fields that are applied as the ocean boundary condition (cf. Methods). These conditions stem from the 100 yr climatological mean of the respective climate states. Differences in ice sheet extent (white area) are caused by grounding line migration.
Extended Data Fig. 5 Temperature and sea ice changes in response to North Atlantic freshwater perturbation.
Shown are surface temperature and sea-ice area fraction changes (iso-lines) for a) interglacial (PIDPERT - PIDCTRL), b) 40ka (40kaPERT - 40kaCTRL) and c) Last Glacial Maximum (LGMPERT - LGMCTRL) conditions, averaged between model years 700-800. The north Atlantic cooling is most pronounced in the LGM perturbation experiment, which is linked to relatively pronounced sea ice cover increase and associated feedbacks. Together with the southern high latitude responses this is indicating a more pronounced interhemispheric seesaw response in surface temperature in the LGM perturbation experiment than under 40 ka or pre-industrial conditions.
Extended Data Fig. 6 Vertical temperature gradient for different climate states in the Atlantic basin.
Zonally averaged temperature gradient (dT/dz) for a) glacial (LGMCTRL), b) interglacial (PIDCTRL) and c) intermediate (40kaCTRL) climate conditions. The coloured circles indicate the geographical location of the climate states shown in Fig. 3.
Extended Data Fig. 7 Perturbed Atlantic overturning stream-function (Sv) at interglacial, intermediate and glacial climate conditions.
Atlantic overturning stream-function (Sv, 106 m3 s−1) in the perturbation experiments representing the average between model years 100-200 for a) interglacial (PIDPERT), b) intermediate (40kaPERT) and c) glacial maximum (LGMPERT) conditions (cf. Fig. 4a). Solid contours indicate clockwise NADW circulation and doted contours anti-clockwise AABW circulation.
Extended Data Fig. 8 Temperature anomaly for the intermediate climate state and the anomaly difference to the glacial state.
Temperature anomaly by AMOC weakening a) for intermediate climate conditions (40kaPERT – 40kaCTRL) between model years 100-200 as a 100 year mean, zonally averaged in the Atlantic sector. Panel b) shows the difference between glacial (Fig. 5b) and intermediate (panel (a) this figure) climate condition anomalies.
Extended Data Fig. 9 Meridional overturning circulation in the Southern Ocean.
Shown are the Eulerian-mean meridional overturning stream function (Sv, 106 m3 s−1) in depth coordinates in the perturbation experiments representing the average between model years 100-200 for a) interglacial (PIDPERT), b) intermediate (40kaPERT) and c) glacial maximum (LGMPERT) conditions (cf. Extended Data Fig. 6). Positive (negative) values indicate clockwise (anticlockwise) circulation. The latitudinal variation in zonal wind-stress induces upwelling between the easterly and westerly wind maxima, and downwelling outside this corridor. Upwelled water can be returned as part of the wind-driven cells south or north of the Antarctic divergence (Ant. Div.) that is linked to a southbound Ekman transport under the influence of Polar easterlies and a northbound Ekman transport under the influence of the westerlies. Along these transport pathways heat and freshwater fluxes at the surface are part of the generalized circulation pattern that feed into the lower or upper limb of the recirculation, respectively. However, the actual upwelling transport largely occurs along surfaces of equal density, with wind and eddy processes playing a central role16. To illustrate such an isopycnal upwelling pathway, we additionally show the σ3 density surface (black line) that characterizes conditions at 3000 m depth and 30°S and upwells towards the latitude belt of the Antarctic Divergence that is subject to strong mixing during austral fall and winter seasons78.
Extended Data Fig. 10 Glacial Atlantic salinity structure in models of the last three PMIP/CMIP generations.
PMIP2/CMIP3 generation models are presented in panels a) to g), PMIP3/CMIP5 in panels h) to o) and PMIP4/CMIP6 in panels p) to s). The individual panels show the zonal mean salinities (PSU) in the Atlantic sector averaged over 100 years for the following models a) CCSM385; b) HadCM3M286; c) COSMOS29,31; d) MIROC 3.289; e) ECBilt-CLIO90; f) IPSL-CM4_V1-MR91; g) FGOALS-1g92; h) CCSM487; i) CNRM-CM593; j) FGOALS-2g94; k) GISS-E2-R95; l) MIROC-ESM96; m) IPSL-CM5A-LR97; n) MPI-ESM-P98; o) MRI-CGCM399; p) AWI-ESM1100,101; q) AWI-ESM2102; r) MIROC-ES2L103,104 and s) MPI-ESM 1.2105,106. Depths and latitudes are displayed in meters (m) and degrees north, respectively. The individual colorbars have been adjusted to reveal mid-depth and abyssal ocean salinity structures.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Knorr, G., Barker, S., Zhang, X. et al. A salty deep ocean as a prerequisite for glacial termination. Nat. Geosci. 14, 930–936 (2021). https://doi.org/10.1038/s41561-021-00857-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-021-00857-3
This article is cited by
-
Evidence for late-glacial oceanic carbon redistribution and discharge from the Pacific Southern Ocean
Nature Communications (2022)
-
A century-long eddy-resolving simulation of global oceanic large- and mesoscale state
Scientific Data (2022)