Abstract
Water electrolysis is a key technology to establish CO2-neutral hydrogen production. Nonetheless, the near-surface structure of electrocatalysts during the anodic oxygen evolution reaction (OER) is still largely unknown, which hampers knowledge-driven optimization. Here using operando X-ray absorption spectroscopy and density functional theory calculations, we provide quantitative near-surface structural insights into oxygen-evolving CoOx(OH)y nanoparticles by tracking their size-dependent catalytic activity down to 1 nm and their structural adaptation to OER conditions. We uncover a superior intrinsic OER activity of sub-5 nm nanoparticles and a size-dependent oxidation leading to a near-surface Co–O bond contraction during OER. We find that accumulation of oxidative charge within the surface Co3+O6 units triggers an electron redistribution and an oxyl radical as predominant surface-terminating motif. This contrasts the long-standing view of high-valent metal ions driving the OER, and thus, our advanced operando spectroscopy study provides much needed fundamental understanding of the oxygen-evolving near-surface chemistry.
Similar content being viewed by others
Main
The fossil fuel-free production of hydrogen (green H2) through water electrolysis has been the topic of intense research efforts for several decades1,2. Only recently, the decreasing cost of electricity from renewable power sources and the possibility to couple electrolysers directly with clean energy sources has become more economically appealing3,4,5. In water electrolysis, the anodic oxygen evolution reaction (OER) remains the bottleneck, which so far limits the overall efficiency and hinders broader industrial application. Although Ru/Ir-based catalysts achieve high efficiencies in polymer electrolyte membrane electrolysers, Co-based electrocatalysts are more economically viable, with high activity in a broad pH range from neutral to alkaline electrolytes6,7,8,9,10,11,12,13. Until now, knowledge-driven catalyst design still lacks in fundamental understanding of the oxygen-evolving near-surface state and of crucial activity- and stability-determining motifs. Thus, understanding the catalytic role of the nanoparticle (NP) size and its influence on the active state properties is of utmost importance to allow a sustainable and (cost-)efficient use of the catalyst mass in a water electrolyser and to narrow the knowledge gap between amorphous and crystalline catalysts. Electrodeposited thin films exhibit notably higher mass-based catalytic activity than their crystalline analogues but the reason is not yet known8. In the supra−4 nm regime, it is known that the mass-based OER activity increases with decreasing NP size and with increasing averaged Co oxidation state9.
Monitoring the evolution of the surface structure during electrocatalysis is highly desirable. However, surface-sensitive operando spectroscopy methods such as X-ray photoelectron spectroscopy (XPS) are still technically challenging14. The current mechanistic knowledge highlights the importance of the (near) surface structural adaptations and the oxygen chemistry for accommodating the required oxidative charge required for the OER8,15,16,17. For example, H1−YCoO2 forms from CoOOH nanosheets11 while Co3O4 transforms reversibly towards CoOx(OH)y with more pronounced Co di-µ-oxo bridging during OER12,13. This reversible adaptation is common for various structurally different CoO and CoOOH catalysts, which also unify in terms of (bulk) Co–O coordination and Co oxidation state8.
Photocatalytic O2 formation on Co3O4 is known to benefit from electronically coupled terminal oxygen sites which enable facile O–O surface superoxide formation, in contrast to less active oxo Co intermediate sites18. The direct coupling of O–O species was independently confirmed utilizing 18O-labelled Co oxide19,20. We recently showed that the accumulation of oxidative charge on IrO2 results in the generation of oxyl species16 and plays a critical role in electrocatalysis. In the case of Co oxides, changes in the oxygen chemical state have been seen using in situ dip-and-pull XPS during OER21 and in Li1−XCoO2 (refs. 22,23). However, neither the oxygen-evolving near-surface (electronic) structure of NP electrocatalysts nor the size-dependent intrinsic catalyst activity have been quantitatively identified, besides the great prior achievements in the mechanistic understanding of crystalline and amorphous thin film or large nanostructured catalysts.
Here we track changes on the near surface of oxygen-evolving CoOx(OH)y NP electrocatalysts with varying surface-to-volume ratio using operando X-ray absorption spectroscopy (XAS). Nanoparticles smaller than 5 nm bridge the knowledge gap among Co-based highly crystalline or X-ray amorphous thin films and NP electrocatalysts. Explicitly, we have monitored size-dependent changes of the averaged Co oxidation state and Co–O distance during OER. Density functional theory (DFT) calculations were performed with a hybrid functional using the Perdew, Burke and Ernzerhof exchange and correlation potential admixed with exact exchange (PBE0). The calculations revealed catalytically relevant near-surface changes through a comparison with selected surface Co–O bonding configurations. In particular, the charge distribution within the Co3+O6 units during OER was analysed to better understand the electronic structure and the accumulation of oxidative charge on the catalyst surface.
Morphology and catalytic activity
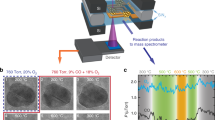
We applied the inverse micelle encapsulation route to prepare size-selected CoOx(OH)y NPs in the range of 1 nm to 9 nm (Fig. 1 and Supplementary Fig. 1). The corresponding size distributions confirm the intended variation of the mean particle size and an increasing monodispersity with decreasing NP size, Fig. 1c. The interparticle distance and low NP loading maximizes the accessibility of exposed sites and minimizes agglomeration during OER.
a–c, AFM images of CoOx(OH)y NPs deposited on SiO2/Si(100) with average heights of: 8.9 ± 1.5 nm (a); 2.0 ± 0.3 nm (b); particle size distributions extracted from a height analysis of AFM images shown here and in Supplementary Fig. 1 (c). The horizontal scale bars in a and b represent 400 nm. The NP heights reported are the mean of the normal distribution and the error the standard deviation.
The surface composition of the CoOx(OH)y NP samples was measured by XPS. In addition, the carbon 1s region for the 5 nm NPs deposited on SiO2/Si(100) exemplarily confirms the removal of the polymer ligand after plasma treatment (Supplementary Fig. 2). For all NP sizes, the Co 2p and O 1s region shows oxidized NPs before electrochemistry. The Co 2p3/2 peak maximum at ~781 eV and satellite structure between 786–790 eV suggest a mixed yet Co2+-rich surface (Supplementary Fig. 3)24,25. The determination of the surface O chemical state of the CoOx(OH)y from the O 1s region is hampered by substrate oxygen contributions (Supplementary Fig. 4). Further details can be found in Supplementary Note 1.
We determined the catalytic activity of the size-selected NPs from potential step experiments, which minimize the influence of the non-catalytic and/or capacitive currents upon an electrochemical activation procedure. We compare the size-dependent mass-based and specific activity using the currents normalized by the Co loading of the electrode and by the NP surface area as shown in Fig. 2a,b, respectively. A direct determination of the electrochemically active CoOx(OH)y surface area was not possible due to the dominating substrate current, Supplementary Fig. 5. In both cases, the current (i) and potential (E) log(i)–E profiles versus the reversible hydrogen electrode (RHE) are linear between 1.58 VRHE and 1.64 VRHE over almost two orders of magnitude in current. The Tafel slopes, in the range of 37–43 mV per decade, are comparable with other Co-based catalysts at pH 13 (refs. 26,27). While we did not detect any size-dependent trend in the Tafel slope, we reveal that the mass activity clearly increases with decreasing NP size (Fig. 2a and Supplementary Table 2, respectively). We explain this in a first approximation by the increasing surface-to-volume ratio and thus the available surface site density.
OER activity determined in N2-saturated 0.1 M KOH exemplified for 1 nm (blue), 4 nm (yellow), 6 nm (magenta) and 9 nm NPs (green). a,b, Tafel plots with the potential E versus the reversible hydrogen electrode (RHE) were extracted from potential step experiments with the current Imass normalized by the Co mass (a) and Ispecific by the calculated NP surface area (b). c, Mass- (black) and surface area normalized current density (red) at 1.62 VRHE for various NP sizes. The Co mass on the glassy carbon electrodes is given in Supplementary Table 1, and the determination of the nominal CoOx(OH)y NP surface area is described in the experimental section. d, Cyclic voltammograms displaying the geometric current density Igeom. and recorded with a scan rate of 100 mV s−1. Redox features are visible for the 9 nm NPs but are less pronounced for smaller NPs. Further data are shown in Supplementary Fig. 5 and Supplementary Table 2. The currents were obtained as the mean with standard deviation from three independent catalytic tests of analogously prepared pristine samples. The NP heights reported are the mean of the normal distribution and the error the standard deviation.
However, the obvious size dependency of the specific activity emphasizes a more complex role of the NP size on the active site density and the catalytic activity (Fig. 2b). To evaluate this relationship, we compare the mass and specific activity at 1.62 VRHE (Fig. 2c). We find that the mass-based current increases from 1.3 ± 0.4 mA µg−1 to 20.4 ± 2.8 mA µg−1 and the specific activity from 0.5 mA \({{{\mathrm{cm}}}}_{{{{\mathrm{NP}}}}}\!^{ - 2}\) to 1.2 ± 0.2 mA \({{{\mathrm{cm}}}}_{{{{\mathrm{NP}}}}}\!^{ - 2}\) for the 9 nm and 1 nm NPs, respectively (Fig. 2c). Although the mass-based activity varies only slightly for the larger NPs, the similar specific activity suggests that the NP surface area primarily determines the activity and thus likely the number of active sites. In contrast, the increasing specific OER activity in the sub-5 nm regime shows that either the active site density on the NP surface increases due to geometric effects or the intrinsic activity of the active sites increases due to electronic effects9. Notably, the CoOx(OH)y NPs exhibit stable current densities during OER at 1.62 VRHE within the time frame of interest for our study (Supplementary Fig. 6). Atomic fore microscopy (AFM) measurements upon OER exposure confirm the morphological stability of the NPs as their height increased by less than 0.5 nm (Supplementary Figs. 6–8). We did not detect any NP agglomeration but observe a minor current decay for the 1 nm NPs due to a slight decrease in the loading.
We also investigated the surface redox electrochemistry by using cyclic voltammetry (Fig. 2d and Supplementary Fig. 5). Only the largest NPs exhibit redox transitions at ~1.15 VRHE and 1.50 VRHE typical for layered CoOx(OH)y (refs. 8,10). These redox features are not detectable for the smaller NPs due to the low NP loading and the (O2-plasma induced) substrate roughness. We refrained from the traditional Co2+/Co3+ and Co3+/Co4+ assignment as it neglects associated changes in the oxygen chemical state and electronic structure. As expected, the CoOx(OH)y NPs hold (near surface) redox transitions, seemingly the prerequisite for the OER, forming (Co3+O6)δ+ surface units.
Size-dependent structural transformation during OER
To identify size-dependent trends in the chemical state and structural adaptations, which are potentially linked to the catalytic activity, we studied size-selected CoOx(OH)y NPs during OER using operando XAS. We followed the redox electrochemistry of the CoOx(OH)y NPs from the Co perspective via X-ray absorption near-edge spectroscopy (XANES) and calibrated the shift of the Co K-edge position with respect to reference CoOx(OH)y compounds using the integral method (Fig. 3, Supplementary Figs. 10–13 and Supplementary Table 7) (ref. 28). The CoOx(OH)y references comprise Co2+ and Co3+-containing compounds with octahedral Co–O bonding environment and NaxCoO2.
Normalized Co K-edge XANES spectra recorded in the as-prepared state, activated at open circuit voltage (OCV) after cyclic voltammetry, during OER at 1.7 VRHE and at OCV after OER of (a) 9 nm and (b) 1 nm NPs. c,d, Comparison of XANES spectra of the 1 nm (blue), 2 nm (brown), 4 nm (yellow), 6 nm (magenta) and 9 nm (green) CoOx(OH)y NPs recorded at 1.7 VRHE during OER (c) and of selected CoOx(OH)y reference compounds for comparison (rs-CoO = rock salt CoO) (d). The insets in a–d highlight the absorption energy position at 0.5 of the normalized XANES. Further details and additional data are provided in Supplementary Figs. 11–13.
We furthermore analysed operando extended X-ray absorption fine-structure (EXAFS) spectra to get insight into the size-dependent trends in the Co–O bonding environment for selected catalyst states and during OER. The corresponding Fourier transformed (FT)-EXAFS spectra of the NPs and of the CoOx(OH)y references are shown in Fig. 4 and Supplementary Fig. 14.
a,b, FT-EXAFS data, with EXAFS data fitting in red, recorded for specific catalyst states of the (a) 9 nm and (b) 1 nm (b) NPs. c, Comparison of FT-EXAFS data under OER conditions at 1.7 VRHE of the 1 nm (blue), 4 nm (yellow), 6 nm (magenta) and 9 nm (green) CoOx(OH)y NPs. d, FT-EXAFS data for CoOx(OH)y reference compounds. Spectra are stacked vertically for clarity and nonlinear least-square fitting are shown in red. Further details regarding the EXAFS fitting model are given in Supplementary Notes 2 and 3. In all spectra, R is the given distance from the center atom, k the photoelectron wavenumber and χ the normalized EXAFS component depending on k.
The XANES and EXAFS data agree well with those recorded for disordered CoOx(OH)y. Both the XANES data and the parameters of the first coordination shell, as extracted from EXAFS, are also similar to those of rock salt (rs-)CoO, β-Co(OH)2 and CoOOH. Nevertheless, the lack of contributions of distant coordination shells suggests a much more disordered structure in our as-prepared NPs than in the well-defined crystalline reference materials. The XANES spectra exhibit a pre-edge feature at ~7,710 eV, a rather featureless onset of the main absorption edge feature at ~7,719 eV and reach maxima between 7,726 eV and 7,728 eV. The average Co oxidation state in the as-prepared samples ranges from ~2.2 to 2.4, with no clear size dependency. The FT-EXAFS spectra show typical peaks for Co–O distances at ~1.5 Å (phase uncorrected) and weak contributions from more distant coordination shells at ~2.5 Å, possibly attributed to di-µ-oxo bridged Co ions8,10.
Upon electrochemical activation, the CoOx(OH)y are oxidized and considerably restructured, as evidenced by the ~1 eV Co K-edge shift (Fig. 3), the 0.05 Å shift in the Co–O peak to ~1.45 Å and the appearance of a more pronounced peak at ~2.5 Å (Fig. 4). These findings suggest the presence of mixed Co2+/Co3+ ions similar to the Co3O4. However, the typical FT-EXAFS peak at ~3.15 Å, linked to the mono-µ-oxo bridges between tetrahedrally and octahedrally coordinated Co ions in the spinel-type Co3O4 is missing12. Thus, we conclude that the activated CoOx(OH)y NPs resemble a layered CoOOH-like structure with primarily di-µ-oxo bridged Co ions. We cannot exclude the formation of 3D cross-linked CoOx(OH)y species, as previously determined for CoO upon OER8. The peak assignment in the FT-EXAFS is confirmed by our results from advanced reverse Monte Carlo (RMC) modelling of EXAFS spectra for reference compounds (rs-CoO and CoOOH) and for NPs with the largest size (9 nm) (Supplementary Figs. 18–21) (refs. 29,30). This size-independent structural convergence towards cobalt-oxyhydroxide matches very well the universal evolution of structural motifs observed for different CoOx(OH)y during OER8.
To quantitatively follow the size-dependent structural changes of the CoOx(OH)y NPs, we performed conventional nonlinear least-square fitting of the EXAFS spectra31 considering the two main Co–O and Co–Co scattering paths (Supplementary Table 6). We identified that the Co–O bond in CoOx(OH)y contracts by ~0.08 Å to ~1.92 ± 0.02 Å upon electrochemical activation compared with the as-prepared state, independent of the NP size. The Co–Co distance varies between 2.84–2.875 Å in the activated state, and both distances for CoOx NPs agree well with the presence of Co2+ and Co3+. The presence of remnant Co2+ ions (probably in the NP core) lead to slightly longer apparent distances compared with those in bulk CoOOH and NaxCoO2 reference compounds (Supplementary Table 6).
During OER, the CoOx(OH)y NPs do not restructure distinguishably, as the XANES and FT-EXAFS spectra are similar to those recorded upon electrochemical activation (Figs. 3–4). However, the Co K-edges shift further suggesting an oxidation of the CoOx(OH)y NPs which, interestingly, gets stronger with decreasing NP size (Fig. 3c). The peak amplitude in the FT-EXAFS differs slightly during OER (Fig. 4c), which we interpret with stronger structural homogeneity towards a CoOOH-like structure of the smaller NPs. We note the similarity of the operando XAS data recorded during OER to those of bulk CoOOH and NaxCoO2 reference compounds. Quantitatively, we determined that the edge shifts by 0.2–1.3 eV during OER (Fig. 5a), and simultaneously, the Co–O and Co–Co distances contract to 1.89–1.90 Å and 2.82–2.86 Å, respectively (Supplementary Tables 7–9). Notably, we also reveal a reversible decrease in the white line intensity, which is obviously larger for the 1 nm NPs as compared with the 9 nm NPs.
a, Average Co oxidation state of the 1 nm (blue), 2 nm (brown), 4 nm (yellow), 6 nm (magenta) and 9 nm (green) CoOx(OH)y NPs calculated by the integral method28 from the operando XANES data shown in Fig. 3 at selected states. b, Reversible change in the charge δ (blue, left axis) and Co–O bond length (red, right axis; Supplementary Table 9) determined by EXAFS fitting during OER as compared with the state after OER. The size dependency of the changes in Co oxidation state and Co–O bond can be described by a parabola, with an extrapolation to 0.287 nm, indicated by the vertical dashed purple line, resembling the outermost surface layer with the thickness of a CoO6 building block. Error bars of the Co oxidation result from the accuracy of the linear calibration (Supplementary Fig. 11). The depicted error bars of the Co–O contraction reflect the standard errors calculated from the EXAFS fitting results. The NP heights reported are the mean of the normal distribution and the error the standard deviation.
These adaptations of the CoOx(OH)y NPs to the OER conditions are reversible for all NP sizes, as upon OER the edge positions agree well with a mixed Co2+/Co3+ oxyhydroxide with a Co–O distance of 1.90–1.92 Å. The latter is furthermore backed up by comparative XPS measurements conducted before and after OER conditioning, as displayed in Supplementary Fig. 22. We attribute these reversible changes to the redox transitions which precede the OER and probably enable the near-surface accumulation of oxidative charge. Quantitatively, the edge shift, especially of the sub-5 nm NPs, would correspond to a chemical state beyond Co3+. We link the relative shift of the Co K-edge to the accumulated oxidative charge δ+ in the (Co3+O6)δ+ units16,19,20,21,32.
Size-dependent Co–O redox chemistry and bond contraction
We emphasize that XANES and EXAFS analyses provide independent evidence for a size-dependent reversible Co–O redox state change and bond contraction of the NPs during OER. Figure 5b shows that both processes get stronger with decreasing NP size, following the surface-to-volume ratio. Thus, the CoOx(OH)y redox and structural adaptation to the reaction conditions appears to proceed on the surface rather than in the bulk. We estimate a near-surface oxidation characterized by a δ of +0.61 ± 0.12 and Co–O contraction of 0.022 ± 0.005 Å by extrapolating the corresponding size-dependent profiles towards the 2.87 Å size of a CoO6 unit, resembling the outermost surface layer. Considering that the magnitude of the observed effect scales with the surface-to-volume ratio, we expect it to be present also in commonly used catalysts with much larger particle sizes. However, in that case, the contribution of the redox processes at the catalyst surface would be challenging to detect by a sample averaging methods such as XAS.
We first investigated the fundamental link between the Co–O redox state and bond length by comparing the experimental findings for the CoOx(OH)y NPs and reference compounds with DFT-PBE0 calculations on bulk CoO and CoOOH. We compared the relative changes in Co edge and the Co–O bond contraction with respect to a CoO0.7(OH)1.3 reference compound chosen due to its structural similarity to the NPs after OER (Supplementary Table 8).
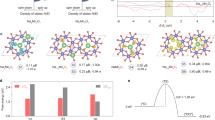
Figure 6a shows two distinct, Co2+-rich and Co3+-rich regimes in which the bulk Co–O bond contracts linearly with the accumulation of oxidative charge. The variation in the Co–O bond length with δ is in the Co2+-rich regime with 0.30 ± 0.02 Å e−1 considerably stronger than in the Co3+-rich regime with 0.036 ± 0.008 Å e−1 (Supplementary Fig. 25). We note that the calculated values for bulk rs-CoO and CoOOH fit very well within their respective regions. Notably, these findings suggest distinct differences in the strength of the Co–O bond in a Co2+-rich or Co3+-rich oxide, while in the former case, removing an electron changes the electronic configuration of the Co2+ ion (from 3d7 to 3d6); in the latter, oxidation has been suggested to also change the O ligand electronic configuration18,19,20,22,23.
a, Bulk Co–O redox state change and bond contraction in CoOx(OH)y NPs as prepared and during OER referred to their state after OER. Co oxide reference compounds (orange) are plotted with respect to CoO0.7(OH)1.3 with an oxidation state of 2.7, which matches the average oxidation state of the NPs after OER. Two distinct encircled linear areas cover the transitions from Co2+ to Co3+-rich regions. Calculated DFT-PBE0 structures for bulk CoO and CoOOH (green hollow squares) with oxidation states of 2+ and 3+, respectively, are also displayed within the two regions. b, Correlation of the reversible Co–O contraction of NPs during OER (blue) and an extrapolation (purple) shown in Fig. 5b with Co3+δ charge extracted from the Co K-edge shift and for different OER-relevant terminations of the coordinatively undersaturated sites (cus) of CoOOH(01\(\bar 1\)2) (green, shown in c) with charge density variation in the Co 3d t2g orbitals extracted from the onsite 3d occupation matrices. c, Co ions are blue, oxygen are red and hydrogen are white. Further information is given in the Supplementary Tables 14 and 16. The depicted error bars of the Co–O contraction reflect the standard errors of EXAFS fitting results. Error bars of the Co oxidation result from the accuracy of the linear calibration (Supplementary Fig. 11). pm is picometer, which is a Si unit of measures.
To reveal how charge accumulation in the Co3+ regime determines the electronic structure and chemistry of the (Co3+O6)δ+ sites during OER, we compared our experimental data with insights from DFT-PBE0 calculations obtained for selected adsorbates on the coordinatively undersaturated sites (cus) of CoOOH(01\(\bar 1\)2) surfaces (Fig. 6, Supplementary Tables 14–16). We calculated the Co–O distances in the octahedral CoO6 bonding environment for various oxygen species adsorbed on the surface, simulating OER-relevant Co–O redox states. We detected a contraction in the case of hydroxide and oxyl adsorbates leading to cus Co–O bond lengths of 1.76 Å and 1.62 Å, respectively, which are clearly much shorter than the calculated Co–O distance of bulk CoOOH (1.910 Å). Furthermore, we calculated the averaged Co–O bond lengths over the terminating CoO6 unit which are between 0.008 Å and ~0.033 Å shorter than in bulk CoOOH. Notably, the cus Co–O contraction is therein partially compensated by elongated bonds to µ2 bridging oxygen (~1.91 Å). In contrast, the cus and averaged Co–O distances increase in the case of adsorbed water and hydro-peroxide species, which does not agree with our current and previous experimental findings and thus are not considered as the dominant motif under stationary OER conditions8. Along this line, we note that the Co–O contraction provokes a distortion of the symmetric octahedral CoO6 ligand field.
Near-surface electronic structure in the OER active state
To link the Co–O bond contraction with the near-surface electronic structure during OER, we furthermore performed charge density analysis for the cus configurations and compared it with our experimental findings. Figure 6b shows the expected trend that the averaged Co–O bond contracts stronger with a decreasing electron density in the Co 3d t2g orbitals compared with bulk CoOOH. This correlation agrees qualitatively and quantitatively very well with the experimentally determined reversible variation of δ.
However, there is no agreement between the Co–O contraction and the calculated total charge Q in the Co 3d orbitals, and interestingly, we detected an increase in electron density in the antibonding eg orbitals, Supplementary Table 16. This compensating charge originates from the O ligands and thus, leads to electron holes therein (oxyl species). This charge reorganization also quantitatively agrees well with the Co–O contraction and nicely explains the weaker Co–O bond contraction in the Co3+-rich regime compared with the Co2+-rich regime. The visible deviation from a symmetric CoO6 coordination due to the (strong) contraction of the cus Co–O bond allows the formation of the Co 3d intermediate/high spin configuration. Interestingly, the Co–O contraction with the variation in calculated total charge matches the one in the Co2+-rich regime. Thus, we conclude that the Co K-edge position (in the Co3+-rich regime) is a valid measure of the t2g empty states, while our finding questions common interpretations of transition metal (for example, Co) K-edge shifts as caused solely by oxidation state changes of the metal ions. Experimentally, the reversible decrease in the white line intensity can be caused by fewer unoccupied antibonding states during OER.
We conclude that the redox transition leads to distinct changes in the electron density for the O adsorbate and the charge densities in the eg and t2g for the calculated oxyl cus species match the extrapolated experimental values for the NP near-surface (Fig. 5b). Thus our findings suggest major electron hole accumulation on the oxygen ions in an Co3+-rich environment hosting the oxidative charge for OER catalysis. We highlight the similarity between CoOx and IrOx electrocatalysts for the OER16,33,34. Previous works already suggested changes in the O chemistry for Co-based electrocatalysts, while not being able to extract structural information on the near-surface M–O bond under OER conditions21. Although we have identified striking correlations between the Co–O oxidation and bond contraction guiding towards the dominating species, we have to consider also a mixed termination on the cus with mixture of OH- and oxyl-terminated cus8,10,35.
Linking the near-surface active state formation and electronic structure to the OER activity shows that with decreasing NP size, the extent of reversible Co–O oxidation increases weaker and the mass activity stronger than expected while simply following the surface-to-volume ratio (Supplementary Fig. 26). This suggests the stronger prevalence of distinct Co–O sites with decreasing NP size, which exhibit a lower degree of (Co3+O6) oxidation and Co–O bond contraction during OER. We emphasize here the similarity to the previously identified beneficial influence of an increased Co3+–O reducibility on the OER activity and CoOOH edge sites, which are also accompanied by a lower Co oxidation state than the in-layer sites, exhibiting lower catalytic turnover8,36.
Finally, our operando methodology under stationary OER conditions probes the equilibrium catalyst state preceding the rate-determining step averaging over all catalytically active sites and the catalytically inactive (or considerably less active) spectator sites. Nonetheless, by studying the size-dependent response of the structure and catalytic activity, we were able to extract a structure–reactivity relationship. However, additional operando experimental studies are required to better understand the near-surface changes in the surface Co–O electronic structure and coordination. Here we especially point out the power of surface-sensitive electron yield or high energy resolution fluorescence detection XAS and resonant inelastic X-ray scattering to reveal changes in the electronic structure37,38.
Conclusions
In summary, we revealed size-dependent trends in the catalytic activity of CoOx(OH)y NPs and in their structural and chemical state changes during the alkaline OER. We show an increasing mass activity with decreasing NP size, which can only be partially assigned to the increasing available NP surface area, because a higher specific activity (referred to as the CoOx(OH)y surface area) was also observed in the sub-5 nm regime.
Operando XAS analysis showed the irreversible formation of CoOx(OH)y with primarily di-µ-oxo bridged Co3+ species under electrochemical conditions and a reversible oxidation and contraction of the Co–O bond under OER conditions. We present fundamental correlations of Co–O redox state and bond length in Co oxides. Most importantly, we show that the average accumulation of oxidative charge and Co–O contraction during OER increases with decreasing NP size, yet to a lesser degree than expected considering the surface-to-volume ratio. By extrapolating the corresponding size-dependent profiles, we could extract quantitative insights into the near-surface structural adaptation of NP catalysts to the OER conditions. Comparing our experimental insights with DFT-PBE0 calculations suggests the presence of an oxyl-adsorbate on the catalyst surface and charge reorganization in the 3d orbitals of the Co3+ ions instead of Co4+ formation during OER. We furthermore emphasize that the lower extent of Co3+δ charge accompanies the enhanced specific catalytic activity. Thus, our findings greatly contribute to the unified operando mechanistic understanding of OER, a prerequisite of knowledge-driven design of improved electrocatalysts for alkaline electrolysis and thus, hydrogen production.
Methods
Preparation of CoOx(OH)y nanoparticles
The inverse micelle encapsulation route was applied to synthesize size-selected CoOx(OH)y NPs. PS-P2VP di-block copolymers (PS(48500)-P2VP(70000), Polymer Source Inc.) were dissolved in toluene and stirred for one day. The so-formed micelles were loaded with a Co(NO3)2 ∙ 6 H2O (99.999%, Alfa Aesar) metal precursor in different ratios towards the polymer head (P2VP molecular weight), and the solution was stirred for two days. The variation of the metal precursor loading yielded six different NP sizes. The loaded micelles were dip coated on a substrate with dip coating speeds ranging from 1–5 cm min−1. Subsequently, the polymer was removed using a plasma etcher (Plasma Prep III, SPI Supplies) with O2 atmosphere (350 mTorr) at a power of 20 W for 20 min. The NPs were available only on one side of the support since we passivated the back side with PTFE tape during dip coating. Depending on the desired NP coverage on the substrate, this process was repeated several times. The NPs were deposited on SiO2/Si(100) wafers (Siegert Wafer) for size determination and on glassy carbon (GC) electrodes (SIGRADUR®, HTW) for the electrochemical measurements. Synchrotron-based operando X-ray absorption spectroscopy measurements were performed after depositing the NPs on a carbon foil (99.95%, GoodFellow).
Ex situ characterization methods of CoOx(OH)y nanoparticles
The size of the NPs deposited on SiO2/Si(100)wafers was determined with atomic force microscopy (AFM, Bruker MultiMode 8) by measuring the NP height and assuming a spherical NP shape, based on previous work from our group39,40,41. Background subtraction and NP counting was carried out using the software Gwyddion. The average height was determined with the centre of a gaussian fit, and the standard deviation is reported from the distribution width.
The cobalt loading for the electrochemical measurements was determined by inductively coupled plasma mass spectrometry (ICP-MS, iCAP RQ, ThermoFisher Scientific). CoOx(OH)y NPs deposited on GC substrates were dissolved in HNO3 (ROTIPURAN® Supra 69%, Card Roth), and an average of three samples was measured for each NP size (Supplementary Table 1) to retrieve the average cobalt loading and standard deviation. The nominal NP surface area and density on the support was calculated from AFM measurements. XAS and ICP-MS yielded the Co:O ratio and the Co loading on the electrode.
XPS measurements were conducted with a monochromatic Al Kα (hν = 1,486.6 eV) X-ray source driven with 300 W at 14.5 kV and equipped with an analyser (Phoibos 150, SPECS). The C 1s signal of the GC electrode with a binding energy of 284.4 eV for graphitic carbon was used for calibration42,43.
Electrochemical characterization
The OER activity measurements were conducted with a three-electrode setup in a commercial electrochemical cell made of PTFE (Pine Research). The working electrode consisted of a GC substrate coated with the NPs and was mounted on a rotating disk electrode (RDE, MSR Rotator, Pine Research), which was rotated at 1,400 r.p.m. To avoid effects of possible accumulated NPs, the edges of the sample were covered with a polyether ether ketone (PEEK) mask, which exposed a defined area of 0.2827 cm2. The counter electrode was a graphite rod (Pine Research) separated with a Zirfon® membrane (Agfa), and the reference electrode was a single junction Hg/HgO (Pine Research). All electrodes were connected to a SP-300 potentiostat (Biologic). The cell was filled with 115 ml of 0.1 M KOH (99.999%, Sigma Aldrich) which was saturated with N2 for at least 15 min before the measurements. The prepared electrolyte was purified with Co(OH)2 following a published routine44. ICP-MS measurements after purification showed 0 ppb Fe, Co and Ni. The reference electrode was calibrated with respect to the reversible hydrogen electrode (RHE) using a HydroFlex® hydrogen reference electrode (Gaskatel). A fresh sample was used for each measurement and characterized following the same electrochemical procedure. At the beginning of each measurement, the Ohmic resistance was measured using potentio-electrochemical impedance spectroscopy and determined by the intersection of the Nyquist plot with the abscissa. All samples were conditioned by 20 cyclic voltammograms from 1.0–1.65 VRHE with 100 mV s−1. The redox behaviour of each catalyst was characterized with a series of cyclic voltammograms. The activity of the NPs was compared by recording staircase potentio-electrochemical impedance spectroscopy: starting at 1.0 VRHE, the potential was stepwise increased up to 1.74 VRHE and held for at least 5 min. At each potential step, impedance spectra were acquired and used for iR compensation afterwards. The currents were averaged over 5 min and over three individual measurements, and standard deviations are reported as error bars. The average currents were corrected by subtracting the respective current recorded for a plasma-treated GC reference sample. All electrode potentials were corrected for the Ohmic resistance and displayed versus RHE, unless stated differently.
Co mass loading and calculation of specific CoOx(OH)y NP surface area
Operando XAS suggests a HyCoOx structure during electrochemistry with constant Co/O ratio 2:1 for all NPs. Changes in the oxidation state and the active structure during OER are induced by protonation/deprotonation. The plausibility of this calculation is shown by Reverse Monte Carlo modelling (Supplementary Figs. 18–21) of the operando spectroscopy data which suggest a CoOOH-like composition. The Co/O ratio and the Co loading of the electrodes (from ICP-MS) were used to calculate the total mass of CoOx(OH)y on the electrode. The total volume of CoOx(OH)Y NP and the overall NP area was calculated using the total mass of CoOx(OH)y with the NP height (from AFM) (Supplementary Table 1).
Operando structural characterization
Operando XAS measurements were carried out at the SAMBA beamline at SOLEIL synchrotron, at the CLAESS beamline at ALBA synchrotron, at the KMC-3 beamline at Bessy II and P64 at the PETRA III (DESY, Hamburg). The samples were mounted in a homemade electrochemical cell containing a 0.1 M KOH electrolyte and were measured at the Co K-Edge (7,708.9 eV). XANES and EXAFS data were acquired under stationary conditions. The CoOx(OH)y NPs were deposited by up to five successive cycles of dip coating and O2-plasma etching to achieve a loading of at least 0.25 µg cm−2 (Supplementary Table 6), on a carbon foil (0.125 mm, 99.95% purity, GoodFellow) to collect EXAFS spectroscopy data. The sample was mounted covering the window of the cell and the catalyst-loaded side pointing towards the inside of the cell with the backside towards the detector, collecting the fluorescence signal and averaging several spectra.
Measurements were conducted in the as-prepared sample state in air, at OCV (open circuit voltage) after an electrochemical conditioning (20 cyclic voltammetry, 1.0–1.65 VRHE at 100 mV s−1), during OER at 1.7 VRHE and at OCV after OER. An iR drop correction during OER was not possible, but based on our experience and comparison with experiments carried out in the laboratory, the iR drop-corrected potential during OER is in the order of 1.6–1.65 VRHE and consistent with the laboratory experiments.
For the XANES and EXAFS measurements of 9 nm NPs at the SAMBA beamline at SOLEIL synchrotron, a Si(220) monochromator was used while higher harmonics were suppressed by a Pd-coated mirror. The dimensions of the beam were 1 × 0.5 mm, and the fluorescence was detected by a 13-channel Ge detector with one ionization chamber. The rs-CoO and Co3O4 reference were measured as pellets in transmission mode. Measurements at the CLAESS beamline at ALBA synchrotron of 2 nm NPs were conducted using a Si(111) monochromator with a beam size of 0.3 × 0.3 mm and six-channel Si drift fluorescence detector. At the CryoEXAFS station at the KMC-3 beamline at BESSY II synchrotron, 1 nm, 4 nm and 6 nm NPs and self-prepared reference compounds were measured. The beamline was equipped with a Si(111) double-crystal monochromator. The detectors possessed two ionization chambers, and the fluorescence yield was measured by a 13-element detector (Ge and Si) and the transmission signal by a Si-PIN photodiode. Intercalated and deintercalated NaxCoO2 references sealed in Kapton were measured in transmission and CoO0.7(OH)1.3 and CoOOH in fluorescence mode. The w-CoO and β-Co(OH)2 pellets were measured in transmission mode at PETRA III P64 Advanced EXAFS beamline at DESY.
Energy alignment, normalization and data analysis were carried out using the Athena31 software. To obtain values for the absorption edge position, the absorption edge was integrated accordingly to the method introduced by Dau et.al28. Thereby, the edge position EEdge is calculated within an interval (E1,E2):
The function µ0 is defined as:
It should be noted that the edge position EEdge does not depend on the interval borders (E1 = 7,705 eV,E2 = 7,730 eV] when using the boundaries µ1 = 0.15 and µ2 = 1, which were chosen to avoid impact of the pre-edge and the white line28. The edge position of reference compounds with known oxidation state was used as a calibration to calculate the oxidation state for the different edge positions with a shift in 2.5 eV for the Co oxide oxidation state as it was done by Risch et.al.45. Details regarding the synthesis of the Co oxide reference compounds is available in the Supplementary Methods.
For quantitative analysis of EXAFS data, conventional least-square fitting to theoretical standards, as implemented in the FEFFIT code was performed46. Theoretical phases and amplitudes were obtained in self-consistent ab-initio calculations with the FEFF8.5 code for bulk rs-CoO and CoOOH materials. The complex exchange correlation Hedin–Lundqvist potential and default values of muffin-tin radii as provided within the FEFF8.5 code were employed47.
Fitting of CoOx(OH)y NPs EXAFS spectra (χ(k)k1, χ(k)k2 and χ(k)k3 simultaneously) was carried out in R-space in the range from 1.0 Å up to 3.0 Å. Fourier transform was carried out in the k range from 3.0 Å−1 up to 10.0 Å−1. We model each EXAFS spectrum with a contribution of two single-scattering paths, corresponding to Co–O and Co–Co bonds. Fitting parameters were the coordination numbers N, average interatomic distances R and disorder factors σ2 for each of these two paths and the correction to the photoelectron reference energy ΔE0. Amplitude reduction factor was obtained in fitting EXAFS spectrum for rs-CoO reference and was found to be close to 1.0. In the case of the CoOx(OH)y references, the R-space range was either 3.0 Å or 3.5 Å, depending on the distance of the Co–Co bond. The Fourier transformation of Co3O4 spinel was performed from 3.0 Å−1 up to 14.0 Å−1 to distinguish between the octahedral and tetrahedral Co–Co bond. For w-CoO, the first scattering path corresponding to Co–O was fitted. EXAFS spectra in Fourier transformed k-space with fits are shown in Supplementary Fig. 15 and the raw data in Supplementary Fig. 16.
RMC simulations
RMC simulations for rs-CoO and CoOOH reference compounds and 9 nm CoOx nanoparticles under OER conditions were carried out using the vAX code29. Simulations started with an initial guess of the structure model, which then was iteratively optimized using simulated annealing and evolutionary algorithm methods with the aim to maximize the agreement between experimental Co K-edge EXAFS spectrum and the corresponding theoretical spectrum calculated for the current structure model. Wavelet transform was used for comparison of theoretical and experimental spectra in the ranges between 3 Å−1 and 10.5 Å−1 in k-space and between 1 Å and 6 Å in R-space. All important scattering paths with the length up to 7 Å were included in simulations of Ref EXAFS spectra, including single-scattering, double-scattering and triple-scattering paths. See ref. 29 for more details of RMC simulations. As the initial guesses for CoO and CoOOH structures, we used equilibrium structures from the Materials Project database48. The bulk CoOOH structure was used also as the initial structure guess for 9 nm CoOx NPs, and the particle size effects were neglected.
Constant kinetic energy XPS
Constant kinetic energy XPS measurements with 550 eV photoelectron energy were carried out at the ISISS endstation of BESSY II synchrotron radiation facility at the Helmholtz–Zentrum Berlin für Materialien und Energie. All measurements were conducted on glassy carbon substrates, and the spectra were aligned to the graphitic C 1s peak measured separately for each excitation energy.
Computational methods
Density functional theory (DFT) calculations were performed at both the Perdew, Burke and Ernzerhof with onsite dd repulsion (PBE + U) level and with the global hybrid functional PBE0. We began by optimizing the geometries at the PBE + U level with U = 3 eV. However, as multiple metal oxidation states must be considered, a single value of U is incapable of correcting the delocalization error of pure PBE for all surfaces49,50,51, which makes the calculation of energetics problematic at the PBE + U level52. Thus, these PBE + U geometries were used as starting points for PBE0 simulations.
All calculations were performed on 11-layer slabs with (01\(\bar 1\)2) termination with the central three layers held fixed during ionic relaxations and approximately 15 Å of vacuum separating periodic images. Simulations were performed using norm-conserving pseudopotentials from the ONCV library53, including semi-core s and p states for Co, with a kinetic energy cut-off of 85 Ry. DFT-PBE0 calculations employed a 170 Ry cut-off for the exact exchange operator and 2.6 Ry cut-off for correcting the divergences at small q vectors. Brillouin Zone integrations were performed using a k-point mesh equivalent to (6 × 3) for the (1 × 1) surface unit cell with 0.005 Ry Gaussian smearing and a (2 × 1) q-point mesh to sample the Fock operator.
For the DFT-PBE0 calculations, 10% and 20% exact exchange (α = 0.10 and α = 0.20) were initially considered. This choice was motivated by simulation on the bulk heterogenite phase of CoOOH. The use of α = 0.20 gives the best agreement between computed and measured lattice constant a, with computed values of a = 2.85 Å and c = 12.88 Å compared with the measured values of a = 2.85 Å and c = 13.15 Å (ref. 54). The calculated band using α = 0.20 was 3.6 eV, which is substantially higher than the reported value of 2.0–2.5 eV (refs. 55,56). At 2.1 eV, the band gap calculated using α = 0.10 reproduces the experimental value of bulk CoOOH together with a = 2.87 Å and c = 12.89 Å. Therefore, we continued with α = 0.10 for simulations of the surfaces. Slabs used for the DFT-PBE0 calculations were generated from the bulk lattice parameter computed with the corresponding fraction of exact exchange.
The role of magnetism was considered in all cases. Bulk CoOOH was found to be non-magnetic, and only surface Co atoms showed magnetic ground states. For these atoms, ferromagnetic and antiferromagnetic coupling of nearest neighbour Co sites were considered with starting magnetizations of ±1 µB on the magnetically active sites. When using α = 0.10, the surface with adsorbed H2O showed no magnetization, while a weak preference for the ferromagnetic solution was found for adsorbed OH and OOH, with adsorption energies of 0.04 eV and 0.01 eV lower in the ferromagnetic case. The stoichiometric surface showed a slight preference for antiferromagnetic ordering; the antiferromagnetic solution of the clean surface is lower than the non-magnetic solution by 0.06 eV per empty site. The adsorption energy of O is independent of the ordering, with the O adsorption energy on antiferromagnetically coupled nearest neighbour Co atoms only 0.002 eV below the ferromagnetic solution. The adsorbed O2 was considered only with ferromagnetic coupling as this surface energy is already rather low.
The OER thermodynamics were computed using the DFT adsorption energies together with the well known computational hydrogen electrode57,58. Entropic corrections for H2O, H2,gas and O2,gas were taken from tabulated values58, where the H2O gas at 0.035 bar was used as the H2O reference state. Zero point energies were computed at the PBE level from finite differences (0.005 Å displacements) using the U = 0 eV geometries for all gas-phase and adsorbed species (Supplementary Table 12). These corrections are given together with the adsorption energies in Supplementary Table 13. From these data, adsorbed water is predicted to be stable at low potentials with adsorbed O2 becoming the stable adsorbate above 1.34 V versus RHE. If O2,ads is assumed to desorb rapidly and is therefore assumed to have a low population, adsorbed OH is predicted to become the dominate adsorbate at 1.38 V versus RHE, at which point the OH-covered surface becomes lower in energy than the surface with H2Oads. At 1.51 V versus RHE, adsorbed OOH becomes more stable than adsorbed OH.
Formal oxidation states were assigned following the method of Sit et al. by projecting the eigenfunctions of the full system onto atomic d-orbitals to generate a (5 × 5) occupation matrix59. The eigenvalues of the occupation matrix are used to define d-orbital occupancy, and the formal oxidation state is defined as the number of d-orbitals with full occupancy, while fractional charges correspond to the eigenvalues.
Data availability
All data supporting the findings of this article are available in the paper, the Supplementary Information and in the source data files. Additional data are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Turner, J. A. Sustainable hydrogen production. Science 305, 972–974 (2004).
Hosseini, S. E. & Wahid, M. A. Hydrogen production from renewable and sustainable energy resources: promising green energy carrier for clean development. Renew. Sustain. Energy Rev. 57, 850–866 (2016).
de Fátima Palhares, D. D. A., Vieira, L. G. M. & Damasceno, J. J. R. Hydrogen production by a low-cost electrolyzer developed through the combination of alkaline water electrolysis and solar energy use. Int. J. Hydrog. Energy. 43, 4265–4275 (2018).
Ardo, S. et al. Pathways to electrochemical solar-hydrogen technologies. Energy Environ. Sci. 11, 2768–2783 (2018).
Jacobsson, T. J., Fjällström, V., Edoff, M. & Edvinsson, T. Sustainable solar hydrogen production: from photoelectrochemical cells to PV-electrolyzers and back again. Energy Environ. Sci. 7, 2056–2070 (2014).
Kanan, M. W. & Nocera, D. G. In situ formation of an oxygen-evolving catalyst in neutral water containing phosphate and Co2+. Science 321, 1072–1075 (2008).
Lu, X. & Zhao, C. Highly efficient and robust oxygen evolution catalysts achieved by anchoring nanocrystalline cobalt oxides onto mildly oxidized multiwalled carbon nanotubes. J. Mater. Chem. A 1, 12053–12059 (2013).
Bergmann, A. et al. Unified structural motifs of the catalytically active state of Co (oxyhydr) oxides during the electrochemical oxygen evolution reaction. Nat. Catal. 1, 711 (2018).
Seo, B. et al. Size-dependent activity trends combined with in situ X-ray absorption spectroscopy reveal insights into cobalt oxide/carbon nanotube-catalyzed bifunctional oxygen electrocatalysis. ACS Catal. 6, 4347–4355 (2016).
Risch, M. et al. Water oxidation by amorphous cobalt-based oxides: in situ tracking of redox transitions and mode of catalysis. Energy Environ. Sci. 8, 661–674 (2015).
Zhou, J. et al. Electrochemically accessing ultrathin Co (oxy)-hydroxide nanosheets and operando identifying their active phase for the oxygen evolution reaction. Energy Environ. Sci. 12, 739–746 (2019).
Bergmann, A. et al. Reversible amorphization and the catalytically active state of crystalline Co3O4 during oxygen evolution. Nat. Commun. 6, 8625 (2015).
Tung, C.-W. et al. Reversible adapting layer produces robust single-crystal electrocatalyst for oxygen evolution. Nat. Commun. 6, 8106 (2015).
Velasco‐Velez, J. J. et al. Photoelectron spectroscopy at the graphene–liquid interface reveals the electronic structure of an electrodeposited cobalt/graphene electrocatalyst. Angew. Chem. Int. Ed. 54, 14554–14558 (2015).
Reier, T. et al. Molecular insight in structure and activity of highly efficient, low-Ir Ir–Ni oxide catalysts for electrochemical water splitting (OER). J. Am. Chem. Soc. 137, 13031–13040 (2015).
Nong, H. N. et al. Key role of chemistry versus bias in electrocatalytic oxygen evolution. Nature 587, 408–413 (2020).
Grimaud, A. et al. Double perovskites as a family of highly active catalysts for oxygen evolution in alkaline solution. Nat. Commun. 4, 2439 (2013).
Zhang, M., De Respinis, M. & Frei, H. Time-resolved observations of water oxidation intermediates on a cobalt oxide nanoparticle catalyst. Nat. Chem. 6, 362–367 (2014).
Ullman, A. M., Brodsky, C. N., Li, N., Zheng, S.-L. & Nocera, D. G. Probing edge site reactivity of oxidic cobalt water oxidation catalysts. J. Am. Chem. Soc. 138, 4229–4236 (2016).
Brodsky, C. N. et al. In situ characterization of cofacial Co(IV) centers in Co4O4 cubane: modeling the high-valent active site in oxygen-evolving catalysts. Proc. Natl Acad. Sci. U.S.A. 114, 3855–3860 (2017).
Favaro, M. et al. An operando investigation of (Ni–Fe–Co–Ce) Ox system as highly efficient electrocatalyst for oxygen evolution reaction. ACS Catal. 7, 1248–1258 (2017).
Yoon, W.-S. et al. Oxygen contribution on Li-ion intercalation−deintercalation in LiCoO2 investigated by O K-edge and Co L-edge X-ray absorption spectroscopy. J. Phys. Chem. B 106, 2526–2532 (2002).
Zhou, J. et al. Voltage-and time-dependent valence state transition in cobalt oxide catalysts during the oxygen evolution reaction. Nat. Commun. 11, 1984 (2020).
Biesinger, M. C. et al. Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Cr, Mn, Fe, Co and Ni. Appl. Surf. Sci. 257, 2717–2730 (2011).
Gupta, R. P. & Sen, S. K. Calculation of multiplet structure of core p-vacancy levels. II. Phys. Rev. B 12, 15–19 (1975).
Gerken, J. B. et al. Electrochemical water oxidation with cobalt-based electrocatalysts from pH 0–14: the thermodynamic basis for catalyst structure, stability, and activity. J. Am. Chem. Soc. 133, 14431–14442 (2011).
Liang, Y. et al. Co3O4 nanocrystals on graphene as a synergistic catalyst for oxygen reduction reaction. Nat. Mater. 10, 780 (2011).
Dau, H., Liebisch, P. & Haumann, M. X-ray absorption spectroscopy to analyze nuclear geometry and electronic structure of biological metal centers—potential and questions examined with special focus on the tetra-nuclear manganese complex of oxygenic photosynthesis. Anal. Bioanal. Chem. 376, 562–583 (2003).
Timoshenko, J., Kuzmin, A. & Purans, J. EXAFS study of hydrogen intercalation into ReO3 using the evolutionary algorithm. J. Condens. Matter Phys. 26, 055401 (2014).
Gurman, S. & McGreevy, R. Reverse Monte Carlo simulation for the analysis of EXAFS data. J. Condens. Matter Phys. 2, 9463 (1990).
Ravel, B. & Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 12, 537–541 (2005).
Sun, S. et al. Shifting oxygen charge towards octahedral metal: a way to promote water oxidation on cobalt spinel oxides. Angew. Chem. 131, 6103–6108 (2019).
Pfeifer, V. et al. The electronic structure of iridium oxide electrodes active in water splitting. Phys. Chem. Chem. Phys. 18, 2292–2296 (2016).
Pfeifer, V. et al. Reactive oxygen species in iridium-based OER catalysts. Chem. Sci. 7, 6791–6795 (2016).
Moysiadou, A., Lee, S., Hsu, C.-S., Chen, H. M. & Hu, X. Mechanism of oxygen evolution catalyzed by cobalt oxyhydroxide: cobalt superoxide species as a key Iitermediate and dioxygen release as a rate-determining step. J. Am. Chem. Soc. 142, 11901–11914 (2020).
Mefford, J. T. et al. Correlative operando microscopy of oxygen evolution electrocatalysts. Nature 593, 67–73 (2021).
Friebel, D. et al. On the chemical state of Co oxide electrocatalysts during alkaline water splitting. Phys. Chem. Chem. Phys. 15, 17460–17467 (2013).
Friebel, D. et al. Identification of highly active Fe sites in (Ni,Fe)OOH for electrocatalytic water splitting. J. Am. Chem. Soc. 137, 1305–1313 (2015).
Behafarid, F. & Roldan Cuenya, B. Nanoepitaxy using micellar nanoparticles. Nano Lett. 11, 5290–5296 (2011).
Ono, L. K., Croy, J. R., Heinrich, H. & Roldan Cuenya, B. Oxygen chemisorption, formation, and thermal stability of Pt oxides on Pt nanoparticles supported on SiO2/Si (001): size effects. J. Phys. Chem. C 115, 16856–16866 (2011).
Jeon, H. S. et al. Operando evolution of the structure and oxidation state of size-controlled Zn nanoparticles during CO2 electroreduction. J. Am. Chem. Soc. 140, 9383–9386 (2018).
Blyth, R. et al. XPS studies of graphite electrode materials for lithium ion batteries. Appl. Surf. Sci. 167, 99–106 (2000).
Sette, F. et al. Lifetime and screening of the C 1s photoemission in graphite. Phys. Rev. B 41, 9766 (1990).
Burke, M. S., Kast, M. G., Trotochaud, L., Smith, A. M. & Boettcher, S. W. Cobalt–iron (oxy)hydroxide oxygen evolution electrocatalysts: the role of structure and composition on activity, stability, and mechanism. J. Am. Chem. Soc. 137, 3638–3648 (2015).
Risch, M. et al. Water oxidation by electrodeposited cobalt oxides—role of anions and redox‐inert cations in structure and function of the amorphous catalyst. ChemSusChem 5, 542–549 (2012).
Newville, M. IFEFFIT: interactive XAFS analysis and FEFF fitting. J. Synchrotron Radiat. 8, 322–324 (2001).
Ankudinov, A., Ravel, B., Rehr, J. & Conradson, S. Real-space multiple-scattering calculation and interpretation of X-ray-absorption near-edge structure. Phys. Rev. B 58, 7565 (1998).
Jain, A. et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Chen, J., Wu, X. & Selloni, A. Electronic structure and bonding properties of cobalt oxide in the spinel structure. Phys. Rev. B 83, 245204 (2011).
Chen, J. & Selloni, A. First principles study of cobalt (hydr)oxides under electrochemical conditions. J. Phys. Chem. C 117, 20002–20006 (2013).
Selcuk, S. & Selloni, A. DFT+U study of the surface structure and stability of Co3O4 (110): dependence on U. J. Phys. Chem. C 119, 9973–9979 (2015).
Kwapien, K., Piccinin, S. & Fabris, S. Energetics of water oxidation catalyzed by cobalt oxide nanoparticles: assessing the accuracy of DFT and DFT+U approaches against coupled cluster methods. J. Phys. Chem. Lett. 4, 4223–4230 (2013).
Hamann, D. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).
Delaplane, R. G., Ibers, J. A., Ferraro, J. R. & Rush, J. J. Diffraction and spectroscopic studies of the cobaltic acid system HCoC2–DCoO2. J. Chem. Phys. 50, 1920–1927 (1969).
Shi, L., Zhao, K. & Liu, S. Photocatalytic degradation of MO and phenol over novel β-CoOOH/g-C3N4 composite under visible light irradiation. Mater. Lett. 228, 121–124 (2018).
Huang, J. et al. Oxyhydroxide nanosheets with highly efficient electron–hole pair separation for hydrogen evolution. Angew. Chem. Int. Ed. 55, 2137–2141 (2016).
Bajdich, M., García-Mota, M., Vojvodic, A., Nørskov, J. K. & Bell, A. T. Theoretical investigation of the activity of cobalt oxides for the electrochemical oxidation of water. J. Am. Chem. Soc. 135, 13521–13530 (2013).
Nørskov, J. K. et al. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892 (2004).
Sit, P. H. L., Car, R., Cohen, M. H. & Selloni, A. Simple, unambiguous theoretical approach to oxidation state determination via first-principles calculations. Inorg. Chem. 50, 10259–10267 (2011).
Acknowledgements
This project was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation): project number 388390466–TRR 247, subproject A4, acknowledged by F.T.H. and project number 406944504–SPP 2080, acknowledged by A.H. Support was received from Germany’s Excellence Strategy–EXC 2008–390540038–UniSysCat. H.S.J. and C.R. acknowledge support from the European Research Council under grant ERC‐OPERANDOCAT (ERC‐725915). F.T.H., A.H. and C.R. acknowledge support by the IMPRS Functional Interfaces in Physics and Chemistry. We thank the Helmholtz–Zentrum Berlin für Materialien und Energie for the allocation of synchrotron radiation beamtime, G. Schuck and M. Haumann for the support at the KMC-3 beamline and M. Hävecker for the support at the ISISS beamline. We acknowledge SOLEIL for provision of synchrotron facilities and we would like to thank A. Zitolo for using the SAMBA beamline. Part of the experiments were performed at CLAESS beamline at ALBA Synchrotron with the collaboration of C. Marini. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III, and we would like to thank V. Murzin and W. Caliebe for using the P64 beamline. We acknowledge Höchstleistungsrechenzentrum Stuttgart for access to the Hawk supercomputer under the ECHO project.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
F.T.H., A.B. and B.R.C. co-wrote the paper. B.R.C. and A.B. designed and supervised the study. F.T.H. performed sample synthesis and characterization and designed and performed all catalytic measurements. F.T.H. and A.B. designed XAS experiments, and F.T.H., A.B. and J.T. analysed the XAS data. T.E.J. performed DFT-PBE0 calculations. F.T.H., A.B., J.T., A.H., H.S.J. and C.R. performed synchrotron experiments. All authors contributed to the discussion and editing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Energy thanks John Mark Martirez, Hao Ming Chen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–4, Methods 1, Tables 1–17, Figs. 1–26 and References 1–12.
Source data
Source Data Fig. 2
Individual current–voltage measurements before averaging for Tafel plots.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haase, F.T., Bergmann, A., Jones, T.E. et al. Size effects and active state formation of cobalt oxide nanoparticles during the oxygen evolution reaction. Nat Energy 7, 765–773 (2022). https://doi.org/10.1038/s41560-022-01083-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41560-022-01083-w
This article is cited by
-
High-spin Co3+ in cobalt oxyhydroxide for efficient water oxidation
Nature Communications (2024)
-
Distance effect of single atoms on stability of cobalt oxide catalysts for acidic oxygen evolution
Nature Communications (2024)
-
Highly efficient anion exchange membrane water electrolyzers via chromium-doped amorphous electrocatalysts
Nature Communications (2024)
-
Exploring dynamic solvation kinetics at electrocatalyst surfaces
Nature Communications (2024)
-
Ion solvation kinetics in bipolar membranes and at electrolyte–metal interfaces
Nature Energy (2024)