Abstract
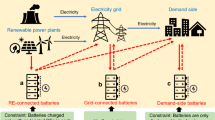
Although there is consensus that both grid extensions and decentralized projects are necessary to approach universal electricity access, existing electrification planning models that assess the costs of decentralized solar energy systems do not include metrics of reliability or quantify the impact of reliability on costs. We focus on stand-alone household solar systems with battery storage in sub-Saharan Africa using the fraction of demand served to measure reliability, and develop a multistep optimization to compute efficiently the least-cost system with the fraction of demand served as a design constraint, and take into account the daily variation in solar resources and costs of solar and storage. We show that the cost of energy is minimized at approximately a 90% fraction of demand served, that current costs increase, on average, by US$0.11 kWh–1 for each additional ‘9’ of reliability, and that this reliability premium could be as low as US$0.03 kWh–1 in a plausible future price scenario.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
All of the data used in this study, with the exception of the sample microgrid load profile from Uganda, is publicly available and referenced here. The sample microgrid load profile is owned by New Sun Road, P.B.C., and can be made available upon reasonable request. Tables on national electrification rates35, grid reliability28 and electricity tariffs34 used to generate Figs. 1 and 6 are included in Supplementary Table 1 for convenience. Solar insolation data are available from the US National Aeronautics and Space Administration38, and the code to download and analyse this data is available at the repositories listed above.
References
Transforming Our World: the 2030 Agenda for Sustainable Development (UN General Assembly, 2015).
Sustainable Energy for All 2017 - Progress toward Sustainable Energy (International Energy Agency and The World Bank, 2017); http://www.worldbank.org/en/topic/energy/publication/global-tracking-framework-2017
Alstone, P., Gershenson, D. & Kammen, D. M. Decentralized energy systems for clean electricity access. Nat. Clim. Chang. 5, 305–314 (2015).
Renewables 2017 Global Status Report (REN21, 2017); http://www.ren21.net/wp-content/uploads/2017/06/170607_GSR_2017_Full_Report.pdf
Cader, C., Bertheau, P., Blechinger, P., Huyskens, H. & Breyer, C. Global cost advantages of autonomous solar–battery–diesel systems compared to diesel-only systems. Energy Sustain. Dev. 31, 14–23 (2016).
Szabó, S., Bódis, K., Huld, T. & Moner-Girona, M. Energy solutions in rural Africa: mapping electrification costs of distributed solar and diesel generation versus grid extension. Environ. Res. Lett. 6, 034002 (2011).
Breyer, C. et al. On the role of solar photovoltaics in global energy transition scenarios. Prog. Photovoltaics Res. Appl. 25, 727–745 (2017).
Bertheau, P., Oyewo, A., Cader, C., Breyer, C. & Blechinger, P. Visualizing national electrification scenarios for sub-Saharan African countries. Energies 10, 1899 (2017).
Lee, K. et al. Electrification for ‘under grid’ households in rural Kenya. Dev. Eng. 1, 26–35 (2016).
McKibben, B. The race to solar power Africa The New Yorker (26 June 2017).
World Energy Outlook 2016 (International Energy Agency, 2016); https://www.iea.org/publications/freepublications/publication/WorldEnergyOutlook2016ExecutiveSummaryEnglish.pdf
Miketa, A. & Saadi, N. Africa Power Sector: Planning and Prospects for Renewable Energy (International Renewable Energy Agency, 2015); http://www.irena.org/DocumentDownloads/Publications/IRENA_Africa_Power_Sector_synthesis_2015.pdf
Miketa, A. & Merven, B. Southern African Power Pool: Planning and Prospects for Renewable Energy (International Renewable Energy Agency, 2013); http://irena.org/DocumentDownloads/Publications/SAPP.pdf
Miketa, A. & Merven, B. West African Power Pool: Planning and Prospects for Renewable Energy (International Renewable Energy Agency, 2013); https://www.irena.org/documentdownloads/publications/wapp.pdf
Wu, G. C., Deshmukh, R., Ndhlukula, K., Radojici, T. & Reilly, J. Renewable Energy Zones for the Africa Clean Energy Corridor (International Renewable Energy Agency, 2015); https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2015/IRENA-LBNL_Africa-RE-_CEC_2015.pdf
Levin, T. & Thomas, V. M. Least-cost network evaluation of centralized and decentralized contributions to global electrification. Energy Policy 41, 286–302 (2012).
Levin, T. & Thomas, V. M. Can developing countries leapfrog the centralized electrification paradigm? Energy Sustain. Dev. 31, 97–107 (2016).
Parshall, L., Pillai, D., Mohan, S., Sanoh, A. & Modi, V. National electricity planning in settings with low pre-existing grid coverage: development of a spatial model and case study of Kenya. Energy Policy 37, 2395–2410 (2009).
Kemausuor, F., Adkins, E., Adu-Poku, I., Brew-Hammond, A. & Modi, V. Electrification planning using Network Planner tool: the case of Ghana. Energy Sustain. Dev. 19, 92–101 (2014).
Szabó, S., Bódis, K., Huld, T. & Moner-Girona, M. Sustainable energy planning: leapfrogging the energy poverty gap in Africa. Renew. Sustain. Energy Rev. 28, 500–509 (2013).
Cader, C., Blechinger, P. & Bertheau, P. Electrification planning with focus on hybrid mini-grids—a comprehensive modelling approach for the global South. Energy Proced. 99, 269–276 (2016).
Lee, M., Soto, D. & Modi, V. Cost versus reliability sizing strategy for isolated photovoltaic micro-grids in the developing world. Renew. Energy 69, 16–24 (2014).
Deichmann, U., Meisner, C., Murray, S. & Wheeler, D. The economics of renewable energy expansion in rural Sub-Saharan Africa. Energy Policy 39, 215–227 (2011).
Nyakudya, R., Mhlanga, S., Chikowore, T. R. & Nyanga, L. in 2013 IEEE International Conference on Industrial Technology 1443–1449 (IEEE, 2013); https://doi.org/10.1109/ICIT.2013.6505884
Szabó, S., Moner-Girona, M., Kougias, I., Bailis, R. & Bódis, K. Identification of advantageous electricity generation options in sub-Saharan Africa integrating existing resources. Nat. Energy 1, 16140 (2016).
Zeyringer, M. et al. Analyzing grid extension and stand-alone photovoltaic systems for the cost-effective electrification of Kenya. Energy Sustain. Dev. 25, 75–86 (2015).
Billinton, R. & Allan, R. N. in Handbook of Reliability Engineering (ed. Pham, H.) 511–528 (Springer-Verlag, Heidelberg, 2003).
Enterprise Surveys (The World Bank, 2017); http://www.enterprisesurveys.org/data/exploretopics/infrastructure#sub-saharan-africa.
Ferrall, I. Measuring electricity reliability of decentralized solar energy systems. C3E Women in Clean Energy Symposium (2017).
Bhatia, M. & Angelou, N. Beyond Connections: Energy Access Redefined Technical Report 008/15 (The World Bank, 2015).
Bucciarelli, L. L. Estimating loss-of-power probabilities of stand-alone photovoltaic solar energy systems. Sol. Energy 32, 205–209 (1984).
Annual Electric Power Industry Report (US Energy Information Administration, 2015); https://www.eia.gov/electricity/data/eia861/
Taneja, J. Measuring Electricity Reliability in Kenya https://www.blogs.umass.edu/jtaneja/files/2017/05/outages.pdf (2017).
Trimble, C., Kojima, M., Perez-Arroyo, I. & Mohammadzadeh, F. Financial Viability of Electricity Sectors in sub-Saharan Africa. Quasi-fiscal Deficits and Hidden Costs Policy Research Working Paper 7788 (The World Bank, 2016); https://data.worldbank.org/data-catalog/affordable-viable-power-for-africa
Access to Electricity (% of Population) (The World Bank, accessed 8 November 2017); https://data.worldbank.org/indicator/EG.ELC.ACCS.ZS
Solar PV in Africa: Costs and Markets (International Renewable Energy Agency, 2016); https://www.irena.org/DocumentDownloads/Publications/IRENA_Solar_PV_Costs_Africa_2016.pdf
Burlig, F. & Preonas, L. Out of the Darkness and Into the Light? Development Effects of Rural Electrification https://ei.haas.berkeley.edu/research/papers/WP268.pdf.
Surface Meteorology and Solar Energy (US National Aeronautics and Space Administration, accessed 19 April 2018); https://power.larc.nasa.gov.
Duffie, J. A. & Beckman, W. A. Solar Engineering of Thermal Processes 4th edn (Wiley, Hoboken, 2013).
Leadbetter, J. & Swan, L. G. Selection of battery technology to support grid-integrated renewable electricity. J. Power Sources 216, 376–386 (2012).
Dunn, B., Kamath, H. & Tarascon, J.-M. Electrical energy storage for the grid: a battery of choices. Science 334, 928–935 (2011).
Divya, K. C. & Østergaard, J. Battery energy storage technology for power systems—an overview. Electr. Power Syst. Res. 79, 511–520 (2009).
Diouf, B. & Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy 76, 375–380 (2015).
Albright, G., Edie, J. & Al-Hallaj, S. A Comparison of Lead Acid to Lithium-ion in Stationary Storage Applications (AllCell Technologies, Chicago, 2012); http://www.batterypoweronline.com/main/wp-content/uploads/2012/07/Lead-acid-white-paper.pdf
Chattopadhyay, D., Bazilian, M. & Lilienthal, P. More power, less cost: transitioning up the solar energy ladder from home systems to mini-grids. Electr. J. 28, 41–50 (2015).
Baurzhan, S. & Jenkins, G. P. Off-grid solar PV: is it an affordable or appropriate solution for rural electrification in Sub-Saharan African countries? Renew. Sustain. Energy Rev. 60, 1405–1418 (2016).
Cole, W. J., Marcy, C., Krishnan, V. K. & Margolis, R. in 2016 North American Power Symposium 1–6 (IEEE, 2016); https://doi.org/10.1109/NAPS.2016.7747866
The Power to Change: Solar and Wind Cost Reduction Potential to 2025 (International Renewable Energy Agency, 2016); http://www.irena.org/DocumentDownloads/Publications/IRENA_Power_to_Change_2016.pdf
Acknowledgements
We thank the US National Science Foundation for supporting this work through the CyberSEES program (award no. 1539585) and are grateful to J. P. Carvallo, R. Shirley, D. Kammen and I. Ferrall for their advice and comments. We also thank J. Sager and New Sun Road, P.B.C., for sharing their insights into decentralized system designs and sample data from their systems.
Author information
Authors and Affiliations
Contributions
J.T.L. contributed the primary development of the optimization program, methods and computer modelling. D.S.C. supervised the research effort. The authors jointly developed the research questions, analysis, conclusions and manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–4, Supplementary Figures 1–5, Supplementary Tables 1–4, Supplementary References
Rights and permissions
About this article
Cite this article
Lee, J.T., Callaway, D.S. The cost of reliability in decentralized solar power systems in sub-Saharan Africa. Nat Energy 3, 960–968 (2018). https://doi.org/10.1038/s41560-018-0240-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41560-018-0240-y
This article is cited by
-
The potential and challenges of off-grid solar photovoltaics in resource-challenged settings: the case of sub-Saharan Africa
Nature Reviews Materials (2024)
-
Potential for small and micro modular reactors to electrify developing regions
Nature Energy (2024)
-
Aquifer conditions, not irradiance determine the potential of photovoltaic energy for groundwater pumping across Africa
Communications Earth & Environment (2023)
-
Real-time mode of operation data analysis to catch the thread-tip denotes the failure cause of the grid-tie PV central inverter
Scientific Reports (2023)
-
A Grid for all Seasons: Enhancing the Integration of Variable Solar and Wind Power in Electricity Systems Across Africa
Current Sustainable/Renewable Energy Reports (2021)