Abstract
Bacteria evolve resistance to antibiotics by a multitude of mechanisms. A central, yet unsolved question is how resistance evolution affects cell growth at different drug levels. Here, we develop a fitness model that predicts growth rates of common resistance mutants from their effects on cell metabolism. The model maps metabolic effects of resistance mutations in drug-free environments and under drug challenge; the resulting fitness trade-off defines a Pareto surface of resistance evolution. We predict evolutionary trajectories of growth rates and resistance levels, which characterize Pareto resistance mutations emerging at different drug dosages. We also predict the prevalent resistance mechanism depending on drug and nutrient levels: low-dosage drug defence is mounted by regulation, evolution of distinct metabolic sectors sets in at successive threshold dosages. Evolutionary resistance mechanisms include membrane permeability changes and drug target mutations. These predictions are confirmed by empirical growth inhibition curves and genomic data of Escherichia coli populations. Our results show that resistance evolution, by coupling major metabolic pathways, is strongly intertwined with systems biology and ecology of microbial populations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
Fastq files with whole-genome sequences of resistant mutants have been uploaded at NCBIs SRA database with the bioproject accession number PRJNA668682.
Code availability
Custom code written in MatLab 2016b to fit dosage–response curves is available from https://github.com/fe-pinheiro/RibosomeTargetingDrugsFitDR.
References
Levy, S. B. & Marshall, B. Antibacterial resistance worldwide: causes, challenges and responses. Nat. Med. 10, S122–S129 (2004).
Lipsitch, M., Bergstrom, C. T. & Levin, B. R. The epidemiology of antibiotic resistance in hospitals: paradoxes and prescriptions. Proc. Natl Acad. Sci. USA 97, 1938–1943 (2000).
Gullberg, E. et al. Selection of resistant bacteria at very low antibiotic concentrations. PLoS Pathog. 7, e1002158 (2012).
Łuksza, M. & Lässig, M. A predictive fitness model for influenza. Nature 507, 57–61 (2014).
Lässig, M., Mustonen, V. & Walczak, A. M. Predicting evolution. Nat. Ecol. Evol. 1, 0077 (2017).
Sommer, M. O., Munck, C., Toft-Kehler, R. V. & Andersson, D. I. Prediction of antibiotic resistance: time for a new preclinical paradigm? Nat. Rev. Microbiol. 15, 689–696 (2017).
Weinreich, D. M., Delaney, N. F., DePristo, M. A. & Hartl, D. L. Darwinian evolution can follow only very few mutational paths to fitter proteins. Science 312, 111–114 (2006).
Palmer, A. C. et al. Delayed commitment to evolutionary fate in antibiotic resistance fitness landscapes. Nat. Commun. 6, 7386 (2015).
Wistrand-Yuen, E. et al. Evolution of high-level resistance during low-level antibiotic exposure. Nat. Commun. 9, 1599 (2018).
Zwart, M. P. et al. Unraveling the causes of adaptive benefits of synonymous mutations in TEM-1 β-lactamase. Heredity 121, 406–421 (2018).
Das, S. G., Direito, S. O., Waclaw, B., Allen, R. J. & Krug, J. Predictable properties of fitness landscapes induced by adaptational tradeoffs. eLife 9, 908574 (2020).
Tenaillon, O. et al. The molecular diversity of adaptive convergence. Science 335, 457–461 (2012).
Toprak, E. et al. Evolutionary paths to antibiotic resistance under dynamically sustained drug selection. Nat. Genet. 44, 101 (2012).
Kryazhimskiy, S., Rice, D. P., Jerison, E. R. & Desai, M. M. Global epistasis makes adaptation predictable despite sequence-level stochasticity. Science 344, 1519–1522 (2014).
Chevereau, G. et al. Quantifying the determinants of evolutionary dynamics leading to drug resistance. PLoS Biol. 13, e1002299 (2015).
Monod, J. The growth of bacterial cultures. Annu. Rev. Microbiol. 3, 371–394 (1949).
Scott, M., Gunderson, C. W., Mateescu, E. M., Zhang, Z. & Hwa, T. Interdependence of cell growth and gene expression: origins and consequences. Science 330, 1099–1102 (2010).
Deris, J. B. et al. The innate growth bistability and fitness landscapes of antibiotic-resistant bacteria. Science 342, 1237435 (2013).
Greulich, P., Scott, M., Evans, M. R. & Allen, R. J. Growth‐dependent bacterial susceptibility to ribosome‐targeting antibiotics. Mol. Syst. Biol. 11, 796 (2015).
Qi, Q., Preston, G. M. & MacLean, R. C. Linking system-wide impacts of RNA polymerase mutations to the fitness cost of rifampin resistance in Pseudomonas aeruginosa. mBio 5, e01562–01514 (2014).
Rodrigues, J. V. et al. Biophysical principles predict fitness landscapes of drug resistance. Proc. Natl Acad. Sci. USA 113, E1470–E1478 (2016).
Tamer, Y. T. et al. High-order epistasis in catalytic power of dihydrofolate reductase gives rise to a rugged fitness landscape in the presence of trimethoprim selection. Mol. Biol. Evol. 36, 1533–1550 (2019).
Basan, M. et al. Overflow metabolism in Escherichia coli results from efficient proteome allocation. Nature 528, 99–104 (2015).
Yang, J. H. et al. A white-box machine learning approach for revealing antibiotic mechanisms of action. Cell 177, 1649–1661 (2019).
Zampieri, M. et al. Metabolic constraints on the evolution of antibiotic resistance. Mol. Syst. Biol. 13, 917 (2017).
Dunphy, L. J., Yen, P. & Papin, J. A. Integrated experimental and computational analyses reveal differential metabolic functionality in antibiotic-resistant Pseudomonas aeruginosa. Cell Syst. 8, 3–14 (2019).
Yang, Y. et al. Changes in the carbon metabolism of Escherichia coli during the evolution of doxycycline resistance. Front. Microbiol. 10, 2506 (2019).
Krause, K. M., Serio, A. W., Kane, T. R. & Connolly, L. E. Aminoglycosides: an overview. Cold Spring Harb. Perspect. Med. 6, a027029 (2016).
Scott, M., Klumpp, S., Mateescu, E. M. & Hwa, T. Emergence of robust growth laws from optimal regulation of ribosome synthesis. Mol. Syst. Biol. 10, 747 (2014).
Paulsen, I. T. & Skurray, R. A. The POT family of transport proteins. Trends Biochem. Sci. 19, 404 (1994).
Yagupsky, P. & Nolte, F. Quantitative aspects of septicemia. Clin. Microbiol. Rev. 3, 269–279 (1990).
Coulthard, M. G. Defining urinary tract infection by bacterial colony counts: a case for 100,000 colonies/ml as the best threshold. Pediatr. Nephrol. 34, 1639–1649 (2019).
Paulander, W., Maisnier-Patin, S. & Andersson, D. I. The fitness cost of streptomycin resistance depends on rpsL mutation, carbon source and RpoS (σS). Genetics 183, 539–546 (2009).
Ruiz, N. & Silhavy, T. J. Sensing external stress: watchdogs of the Escherichia coli cell envelope. Curr. Opin. Microbiol. 8, 122–126 (2005).
Kurabayashi, K., Hirakawa, Y., Tanimoto, K., Tomita, H. & Hirakawa, H. Role of the CpxAR two-component signal transduction system in control of fosfomycin resistance and carbon substrate uptake. J. Bacteriol. 196, 248–256 (2014).
Galdiero, S. et al. Microbe–host interactions: structure and role of Gram-negative bacterial porins. Curr. Protein Pept. Sci. 13, 843–854 (2012).
Shigemura, K. et al. Association of overexpression of efflux pump genes with antibiotic resistance in Pseudomonas aeruginosa strains clinically isolated from urinary tract infection patients. J. Antibiot. 68, 568–572 (2015).
Boolchandani, M., D’Souza, A. W. & Dantas, G. Sequencing-based methods and resources to study antimicrobial resistance. Nat. Rev. Genet. 20, 356–370 (2019).
Shoval, O. et al. Evolutionary trade-offs, Pareto optimality, and the geometry of phenotype space. Science 336, 1157–1160 (2012).
Li, Y., Petrov, D. A. & Sherlock, G. Single nucleotide mapping of trait space reveals Pareto fronts that constrain adaptation. Nat. Ecol. Evol. 3, 1539–1551 (2019).
Stokes, J. M., Lopatkin, A. J., Lobritz, M. A. & Collins, J. J. Bacterial metabolism and antibiotic efficacy. Cell Metab. 30, 251–259 (2019).
Ojkic, N. et al. A roadblock-and-kill mechanism of action model for the DNA-targeting antibiotic ciprofloxacin. Antimicrob. Agents Chemother. 64, e02487–19 (2020).
Kavčič, B., Tkačik, G. & Bollenbach, T. Minimal biophysical model of combined antibiotic action. PLoS Comput. Biol. 17, e1008529 (2020).
Miller, J. A Short Course in Bacterial Genetics: A Laboratory Manual and Handbook for Escherichia coli and Related Bacteria (Cold Spring Harbor Lab Press, 1992).
Gillet-Markowska, A., Louvel, G. & Fischer, G. bz-rates: a web tool to estimate mutation rates from fluctuation analysis. G3 5, 2323–2327 (2015).
Deatherage, D. E. & Barrick, J. E. in Engineering and Analyzing Multicellular Systems. Methods in Molecular Biology (Methods and Protocols) Vol. 1151 (eds Sun L. & Shou W.) 165–188 (Humana Press, 2014).
Hui, S. et al. Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol. Syst. Biol. 11, 784 (2015).
Scott, M. & Hwa, T. Bacterial growth laws and their applications. Curr. Opin. Biotechnol. 22, 559–565 (2011).
Jun, S., Si, F., Pugatch, R. & Scott, M. Fundamental principles in bacterial physiology—history, recent progress, and the future with focus on cell size control: a review. Rep. Prog. Phys. 81, 056601 (2018).
Greulich, P., Doležal, J., Scott, M., Evans, M. R. & Allen, R. J. Predicting the dynamics of bacterial growth inhibition by ribosome-targeting antibiotics. Phys. Biol. 14, 065005 (2017).
Perfeito, L., Ghozzi, S., Berg, J., Schnetz, K. & Lässig, M. Nonlinear fitness landscape of a molecular pathway. PLoS Genet. 7, e1002160 (2011).
Tritton, T. R. Ribosome–tetracycline interactions. Biochemistry 16, 4133–4138 (1977).
Nierhaus, D. & Nierhaus, K. H. Identification of the chloramphenicol-binding protein in Escherichia coli ribosomes by partial reconstitution. Proc. Natl Acad. Sci. USA 70, 2224–2228 (1973).
Praski Alzrigat, L., Huseby, D. L., Brandis, G. & Hughes, D. Fitness cost constrains the spectrum of marR mutations in ciprofloxacin-resistant Escherichia coli. J. Antimicrob. Chemother. 72, 3016–3024 (2017).
Pacheco, J. O., Alvarez-Ortega, C., Rico, M. A. & Martínez, J. L. Metabolic compensation of fitness costs is a general outcome for antibiotic-resistant Pseudomonas aeruginosa mutants overexpressing efflux pumps. mBio 8, e00500–e00517 (2017).
Dai, X. et al. Reduction of translating ribosomes enables Escherichia coli to maintain elongation rates during slow growth. Nat. Microbiol. 2, 16231 (2016).
Dennis, J. E. & Woods, D. J. New Computing Environments: Microcomputers in Large-scale Computing Vol. 27 (Siam, 1987).
Keseler, I. M. et al. The EcoCyc database: reflecting new knowledge about Escherichia coli K-12. Nucleic Acids Res. 45, D543–D550 (2017).
Acknowledgements
We acknowledge discussions with M. Scott, T. Bollenbach, S. Kryazhimskiy, A. de Visser, D. Marmiroli and I. Gordo. This work has been partially funded by Deutsche Forschungsgemeinschaft grant no. CRC 1310 to M.L. and Swedish Research Council grant no. 2017-01527 to D.I.A.
Author information
Authors and Affiliations
Contributions
All authors were involved in the investigation, original draft writing, review and editing of the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Ecology & Evolution thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Membrane-associated resistance mutations: genes, pathways and functions.
See ref. 58 for a description of genes, encoded proteins and their physiological role.
Extended Data Fig. 2 Drug-dependent growth inhibition curves.
(a) Rich medium (LB, liquid culture). Data points (black) show growth rates for three replicates of the wild type and of membrane mutants at different drug levels d (measured in units of the half-inhibitory concentration of the wild type, \(d_{50}^{{\mathrm{wt}}} = 8.7{\mathrm{mg}}/{\mathrm{l}}\)). Coloured points show the average growth across replicates and bars indicate rms. experimental uncertainties, colours mark the drug level of the Luria–Delbrück assay used to elicit each mutant, \(d_{{\mathrm{LD}}}/d_{50}^{{\mathrm{wt}}} = 0.9\), 1.8, 3.6 (violet, pink, red). The wild type is shown for comparison (grey curves). Empirical growth inhibition curves, \(\lambda (d)/\lambda _0^{{\mathrm{wt}}} = G(d;W,d^ \ast ,\lambda ^ \ast )\) (lines) involve three independent fit parameters for each mutant: the drug-free growth rate, \(W = \lambda _0/\lambda _0^{{\mathrm{wt}}}\) and the drug response parameters19 d*, λ*; see equation (17). These fits also produce estimates of the membrane transport rates, γin and γout and of the characteristic drug levels dc and d50. For each mutant, the critical point (dc, G(dc)) (square) gives the empirical growth rate at the predicted critical drug concentration; this point is used in Fig. 4a. Inferred growth and resistance parameters for all membrane mutants are listed in the table in Extended Data Fig. 3, raw data are reported in Supplementary Table 1. (b) Minimal glycerol liquid medium. Data points show growth rates of the wild type and of Cpx stress response mutants elicited at \(d_{{\mathrm{LD}}}/d_{50}^{{\mathrm{ref}}} = 0.9\). All drug levels are measured in units of \(d_{50}^{{\mathrm{ref}}} = 8.7{\mathrm{mg}}/{\mathrm{l}}\). The fit procedure is detailed in Methods.
Extended Data Fig. 3 Growth and resistance data of membrane mutants.
(1) Mutant number. (2) Drug level of Luria–Delbrück assay, \(d_{{\mathrm{LD}}}/d_{50}^{{\mathrm{wt}}}\). (3,4,5) Posterior average parameters of the membrane evolution model: resistance cost, \(W = \lambda _0/\lambda _0^{{\mathrm{wt}}}\); drug response parameters, d*/\(d_ \ast ^{{\mathrm{wt}}}\), \(\lambda _ \ast /\lambda _ \ast ^{{\mathrm{wt}}}\). (6,7) Membrane transport rates: uptake rate \(\varepsilon = \gamma _{{\mathrm{in}}}/\gamma _{{\mathrm{in}}}^{{\mathrm{wt}}}\); release rate, \(\gamma _{{\mathrm{out}}}/\gamma _{{\mathrm{out}}}^{{\mathrm{wt}}}\). (8) Resistance, \(R = d_{50}/d_{50}^{{\mathrm{wt}}}\). (9) Critical drug level, \(d_{\mathrm{c}}/d_{50}^{{\mathrm{wt}}}\). All concentrations and rates are reported in units of the wild-type parameters \(d_{50}^{{\mathrm{wt}}} = 8.66{\mathrm{mg}}/{\mathrm{l}},d_ \ast ^{{\mathrm{wt}}} = 3.13{\mathrm{mg}}/{\mathrm{l}}\), \(\lambda _0^{{\mathrm{wt}}} = 2/{\mathrm{h}},\lambda _ \ast ^{{\mathrm{wt}}} = 0.37/{\mathrm{h}}\). Measured growth rates and inferred growth inhibition curves are shown in Extended Data Fig. 2. Inference procedures are detailed in section 3 of Methods.
Extended Data Fig. 4 Membrane-based evolution of drug resistance.
(a) Measured streptomycin uptake rate for representative membrane mutants relative to the wild type. Label numbers identify specific mutants listed in Extended Data Fig. 2. Dots show measurements for two replicates. (b–d) Model-based inference. We compare (b) uptake rate, \(\varepsilon = \gamma _{{\mathrm{in}}}/\gamma _{{\mathrm{in}}}^{{\mathrm{wt}}}\), (c) drug-free growth rate, \(W = \lambda _0/\lambda _0^{{\mathrm{wt}}}\) and (d) resistance, \(R = d_{50}/d_{50}^{{\mathrm{wt}}}\), of membrane mutants obtained from our full inference procedure with the corresponding values from a constrained model with fixed parameter \(\lambda _ \ast = 2\left( {\gamma _{{\mathrm{out}}}\kappa _t^0K} \right)^{1/2} = \lambda _ \ast ^{{\mathrm{wt}}}\). Bars show rms. measurement errors. Drug-free growth and resistance show insignificant changes, the uptake rate changes significantly in only three mutants. Hence, variation of the parameter γout does not affect the inference of the membrane model (equation (3)), of the evolutionary trade-off W(R) (Fig. 3) and of the empirical data reported in Fig. 4.
Extended Data Fig. 5 Comparison of evolutionary resistance mechanisms.
Evolutionary trade-off curves, W(R) and maximum-growth trajectories, Gc(d), are shown for the following models: (a) Minimal membrane permeability evolution (reduction of uptake rates, \(\gamma _{{\mathrm{in}}}/\gamma _{{\mathrm{in}}}^{{\mathrm{wt}}}\) = \(\kappa _n/\kappa _n^{{\mathrm{wt}}}\), at constant release rate, \(\gamma _{{\mathrm{out}}}/\gamma _{{\mathrm{out}}}^{{\mathrm{wt}}} = 1\), as in main text) and an extended model (reduction of uptake and release rates, \(\gamma _{{\mathrm{in}}}/\gamma _{{\mathrm{in}}}^{{\mathrm{wt}}}\) = \(\kappa _n/\kappa _n^{{\mathrm{wt}}}\) = \(\gamma _{{\mathrm{out}}}/\gamma _{{\mathrm{out}}}^{{\mathrm{wt}}}\)) are compared in the growth regime of irreversible drug metabolism19 (\(r^{{\mathrm{wt}}} \gg 1\)). In this regime, release rates have a negligible influence on growth and resistance, supporting use of the minimal model. Model parameters: \(q^{{\mathrm{wt}}} = 5.9,r^{{\mathrm{wt}}} = 5.4\) as in main text. (b,c) Evolution of drug efflux pumps (increase of drug release rate by overexpression of efflux genes, \(\gamma _{{\mathrm{out}}}/\gamma _{{\mathrm{out}}}^{{\mathrm{wt}}} = \varphi _{{\mathrm{efl}}}/\varphi _{{\mathrm{efl}}}^{{\mathrm{wt}}}\)) and minimal membrane evolution are compared in regimes of irreversible (\(r^{{\mathrm{wt}}} \gg 1\)) and reversible growth (\(r^{{\mathrm{wt}}} \lesssim 1\)). Efflux pumps are predicted to be relatively inefficient specifically under irreversible growth. Model parameters: efflux cost parameter, cefl = 5×10−3, 1 × 10−2, 1.5×10−2 (top to bottom), qref = 5.9, rref = 5.4 (irreversible regime, as in main text), qwt = 5.9, rwt = 0.9 (reversible regime). The reversible regime can be attained by applying a drug with reduced ribosome binding affinity (that is, with increased equilibrium constant K) for a given wild-type (that is, at constant \(\lambda _0^{{\mathrm{wt}}}\)). This results in increased drug response parameters \(\lambda _ \ast ^{{\mathrm{wt}}}\) and \(d_ \ast ^{{\mathrm{wt}}}\) compared to the reference drug; see equation (17).
Extended Data Fig. 6 Resistance mutation spectra in evolution and selection assays.
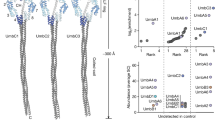
(a) Spectrum of resistance mutation rates, U(R), inferred from Luria–Delbrück assays (cyan: membrane mutations; orange: rpsL mutations). Dashed horizontal lines indicate threshold population sizes; resistance effects above a given line are likely to be represented in a population of given size N. (b) Resulting spectrum of mutant growth rates in rich LB at different drug levels, U(G;d), aggregated from the mutation rate spectrum U(R), the fitness model for membrane mutations and the measured growth rates of target mutations. Arrows mark the maximum growth rate attainable by short-term evolution at a given population size. The low-growth component corresponds to unobservable low-resistance mutants. (c,d) Resulting normalized distributions of resistance effects and growth rates of mutant colonies in Luria–Delbrück assays, PLD(R;d) and PLD(G;d), at different drug levels. Filled squares indicate growth rate segments with probability > 0.04, dots mark observed mutants (as in Fig. 5a).
Supplementary information
Rights and permissions
About this article
Cite this article
Pinheiro, F., Warsi, O., Andersson, D.I. et al. Metabolic fitness landscapes predict the evolution of antibiotic resistance. Nat Ecol Evol 5, 677–687 (2021). https://doi.org/10.1038/s41559-021-01397-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41559-021-01397-0
This article is cited by
-
Steering and controlling evolution — from bioengineering to fighting pathogens
Nature Reviews Genetics (2023)
-
Quantitative systems-based prediction of antimicrobial resistance evolution
npj Systems Biology and Applications (2023)
-
CanB is a metabolic mediator of antibiotic resistance in Neisseria gonorrhoeae
Nature Microbiology (2023)
-
Shaping bacterial gene expression by physiological and proteome allocation constraints
Nature Reviews Microbiology (2023)
-
Translating eco-evolutionary biology into therapy to tackle antibiotic resistance
Nature Reviews Microbiology (2023)