Abstract
Theory predicts that rising CO2 increases global photosynthesis, a process known as CO2 fertilization, and that this is responsible for much of the current terrestrial carbon sink. The estimated magnitude of the historic CO2 fertilization, however, differs by an order of magnitude between long-term proxies, remote sensing-based estimates and terrestrial biosphere models. Here we constrain the likely historic effect of CO2 on global photosynthesis by combining terrestrial biosphere models, ecological optimality theory, remote sensing approaches and an emergent constraint based on global carbon budget estimates. Our analysis suggests that CO2 fertilization increased global annual terrestrial photosynthesis by 13.5 ± 3.5% or 15.9 ± 2.9 PgC (mean ± s.d.) between 1981 and 2020. Our results help resolve conflicting estimates of the historic sensitivity of global terrestrial photosynthesis to CO2 and highlight the large impact anthropogenic emissions have had on ecosystems worldwide.
Similar content being viewed by others
Main
Globally, photosynthesis results in the single largest flux of carbon dioxide (CO2) between the atmosphere and the biosphere1,2. Long-term changes in photosynthesis, for example in response to rising atmospheric CO2, could therefore provide an important feedback to climate change3,4,5. Global terrestrial photosynthetic carbon uptake cannot be observed directly, however, and must instead be either predicted by terrestrial biosphere models (TBMs) or inferred from proxies2. The multiple long-term proxies from which changes in global terrestrial photosynthesis are derived include satellite-based estimates6,7, ice-core records of carbonyl sulfide (COS)8 and herbarium samples of deuterium isotopomers9, along with information gleaned from the seasonal cycle of atmospheric CO2 (ref. 10). Despite the importance of photosynthesis, however, and the multiple proxies that exist, there is no consensus about the expected historic change in terrestrial photosynthesis due to rising CO2 (refs. 3,4,5,6,7,8,9,10,11,12).
Satellite-based estimates of global terrestrial photosynthetic carbon uptake are derived from observations of spatiotemporal variations in surface reflectance, from which vegetation solar energy absorption can be derived. As they integrate land surface observations, they are often regarded as a benchmark to which TBMs should be compared11. Such comparisons generally suggest that TBMs overestimate the change in global terrestrial photosynthesis due to too high a sensitivity of photosynthesis to increasing CO2 (refs. 6,11). However, satellite–TBM comparisons are mired by the fact that most satellite-based estimates, be they machine learning (ML) or algorithmically based, do not incorporate the universally observed direct effect of increasing CO2 on the light-use efficiency (LUE) of leaves of C3 vegetation13. This is because the direct effect of increasing CO2 on LUE is not directly observable from space14. In contrast, observation-based proxies, based on ice-core records of COS8,15, eddy-covariance networks12 and herbarium and field-based deuterium isotopomers9, suggest that TBMs may underestimate the sensitivity of global photosynthesis to CO2. TBMs themselves show a large range of sensitivities of global terrestrial photosynthesis to CO2 (refs. 10,16,17), though few demonstrate sensitivities as low as the average satellite-inferred values6,14 or typically as high as those derived from the COS or deuterium proxies8,9,17. The spread in estimates of the sensitivity of global terrestrial photosynthesis to CO2 and the lack of a global constraint, constitutes a large source of uncertainty in future projections of the Earth system18 and hinders attribution of the various processes responsible for long-term changes in the global terrestrial carbon cycle.
Here, we use remote sensing (RS) observations informed with ecological optimality theory to help constrain the historic response of photosynthesis to rising CO2. We develop a method to incorporate the direct effect of CO2 on the rate of canopy-level terrestrial gross primary photosynthesis (GPP) in established satellite-based approaches. We do so using first-principles theory of photosynthetic carbon fixation19,20 and generate 30-year global datasets of satellite-derived GPP. In addition, we identify an emergent multimodel relationship21,22,23 between the modelled terrestrial carbon sink and the sensitivity of photosynthesis to CO2 from the Trends in Net Land–Atmosphere Carbon Exchanges project (TRENDY24). When combined, these approaches constrain the range of plausible estimates of the historic effect of CO2 on global GPP, resolving the large apparent difference between satellite- and TBM-inferred sensitivities of GPP to historic changes in atmospheric CO2.
We reconciled the apparent difference between the TBM-inferred and satellite-based estimates of the sensitivity of GPP to CO2 (Fig. 1) by using first-principles theory to incorporate the direct effect of increasing CO2 on C3 LUE in the satellite-based estimates. We refer to RS estimates that incorporate theory of the direct effect of CO2 on LUE as the modified RS-based methods hereafter. The direct effect of CO2 on LUE reflects the increasing competitiveness of CO2 relative to O2 for the active sites of the ribulose-1,5-bisphosphate carboxylase-oxygenase (RuBisCO) enzyme and the increasing competitiveness of CO2 as atmospheric concentrations rise (Methods). To do so we considered two distinct classes or satellite-based estimates. The first is a commonly used LUE approach based on the Moderate Resolution Imaging Spectroradiometer (MODIS) algorithm (the MA approach) and the second is an ML approach that integrates both satellite and ground observations of ecosystem carbon fluxes. The direct effect of increasing CO2 on the LUE of canopy photosynthesis13 was roughly twice as large as the indirect effect of increasing canopy leaf area and thus increasing the fraction of absorbed photosynthetically active radiation(fAPAR), represented in the ML and MA approaches (Fig. 1a,b). The long-term sensitivity of the RS-based estimates of GPP modified to account for both the direct \((\beta _{{\rm{R}}}^{{\rm{LUE}}})\) and indirect (\({\beta }_{{\rm{R}}}^{{f\rm{APAR}}}\)) effect of increasing CO2 (\({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\); equation (1)) was 0.50 ± 0.1 (mean ± s.d.) and 0.46 ± 0.1 for the ML and MA approaches, respectively (Fig. 1b), compared to 0.16 ± 0.05 and 0.16 ± 0.06 for the original ML and MA-based estimates, respectively (Fig. 1b). The long-term increase in GPP from the updated RS-based estimates thus more closely approximated that of the TBM ensemble mean (\({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) = 0.59 ± 0.16) (Fig. 1b). The modified RS-based methods predict a 7.27 ± 0.7% (ML) and 6.72 ± 0.9% (MA) increase in global annual GPP for a 14.5% increase in atmospheric CO2 between 1982 and 2012.
a, Relative changes in global terrestrial photosynthesis (∆GPP, %) from 1982 (CO2 = 341 ppm) to 2012 (CO2 = 391 ppm) based on simulations from process-based models in the TRENDY project model ensemble (orange, mean ± s.d.) and two different satellite approaches (empirical MODIS algorithm (MA, solid lines); a machine learning method (ML, dashed lines)). Estimates from the satellite approaches were obtained allowing for an effect of increasing CO2 on either the fAPAR (red lines, dots), the LUE of photosynthesis (blue line) or both fAPAR and LUE (black lines, dots). b, Inferred CO2 sensitivities (\({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\); Methods) from the data presented in a, for the standard satellite-based approaches using ML and the MODIS algorithm (MA) with the CO2 effect on GPP manifest through changes in fAPAR, the modified MA approach with a CO2 effect only on LUE (MA, only LUE) and both ML and MA satellite RS-based approaches with an effect of increasing CO2 on both LUE and fAPAR. Black error bars represent the mean standard error of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) for each product (MA, ML) or the mean standard error across TRENDY models.
Despite the agreement between the updated satellite methods and the TBM model ensemble (Fig. 1b), there is a large spread in individual TBM sensitivities and the true sensitivity is uncertain because of the lack of a comparable observational record. To address this issue, we proposed a constraint on the historic response of photosynthesis to rising CO2 by combining the TRENDY modelled sensitivity of global GPP, for which no direct observations exist, with the magnitude of the cumulative global terrestrial residual carbon sink between 1982 and 2016 (SLAND), for which there are constrained estimates25,26. Using cumulative SLAND estimates as opposed to shorter time periods reduces the influence of annual or decadal random error. Model sensitivities of photosynthesis to CO2 (Supplementary Table 2) were positively correlated (r = 0.70, P < 0.01) with the magnitude of the modelled cumulative terrestrial sink on a multidecadal scale (Fig. 2a), with a stronger CO2 fertilization effect leading to a larger modelled cumulative sink. This emergent relationship21,22,23, provides an opportunity to constrain the wide range in estimates of the sensitivity of GPP to CO2 with the observed magnitude of SLAND, particularly when combined with the results of the modified RS-based estimates. The full distribution, which includes the TBMs (Supplementary Table 2) and the original RS-based estimates, provides an estimate of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) of 0.54 ± 0.21 (mean ± s.d.; Fig. 2b), which is lower than that derived from the distribution of TBMs (\({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) = 0.59 ± 0.16). The posterior TBM distribution, formed by bootstrapping the cumulative land-sink emergent constraint relationship (Fig. 2a) provides a constrained estimate of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) of 0.62 ± 0.14 (Fig. 2b). This is 30% lower than the maximum unconstrained estimate and over 200% higher than that of the original RS-based approaches. The constrained distribution represents a 33% reduction in uncertainty compared to the full distribution of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) (Fig. 2b) and a 13.5% reduction compared to the unconstrained TBM ensemble (Fig. 2b).
a, The relationship between the modelled sensitivity of GPP to CO2 (\({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\), TRENDY experiment S1: dynamic CO2 only) and the modelled cumulative terrestrial carbon sink (PgC, TRENDY experiment S3: dynamic CO2, climate and land use). Individual TRENDY model details and \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) values are listed in Supplementary Table 2. The red line and shaded area show the best linear fit across models and the associated prediction standard error (dashed red) and standard deviation of prediction error (dashed grey) intervals. The vertical dashed lines shows the cumulative residual terrestrial carbon sink (mean, s.d.) between 1982 and 2016 as estimated by the Global Carbon Project27. b, The unconstrained probability density function (PDF) distribution of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) across all original estimates (TRENDY models and the original RS-based approaches; dotted line, grey bars) and the unconstrained PDF of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) across the TRENDY TBMs (dashed black line). The orange area represents the conditional probability distribution derived by applying the constraint from a to the model ensemble.
Results from the updated RS estimates and the emergent constraint provide a point of comparison for other reported estimates of the sensitivity of global terrestrial photosynthesis to CO2. A long-term COS proxy has been proposed8, which simulates photosynthetic change on the basis of a mass balance of global COS sources and sinks from 1900 to 2013 and suggests an increase in photosynthesis equivalent to an effective \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) of 0.94 (Supplementary Table 1). This is comparable to the highest sensitivity of the TBM models used here17. The COS estimate, however, integrates over a longer time period and therefore potentially captures changes in the land surface unrelated to CO2, such as reforestation and the agricultural green revolution27, and is thus not directly comparable to the emergent constraint and updated RS estimates presented here. Another proxy, based on deuterium isotopomers gathered from herbarium specimens and field trials9, suggests an historic change equivalent to a \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) of 1.03 (Supplementary Table 1). Although higher than that derived from COS, the deuterium isotopomer estimate reflects the effect of increasing CO2 on photosynthesis for leaves in full sunlight. As shaded leaves experience stronger light limitation, which results in a lower sensitivity to CO2, COS-based estimates could thus reasonably be expected to be higher than the canopy integrated sensitivity. Our results indicate that such larger implied sensitivities are probably overestimates (Fig. 2).
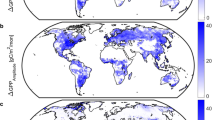
The closer agreement between the updated RS approaches and the TBMs (Fig. 1) allows for their response to CO2 to be probed more deeply. The sensitivity of C3 photosynthesis to CO2 increases strongly with temperature28 (Fig. 3a; equations (2)–(7)) because the suppression of oxygenation by RuBisCO with increasing CO2 is greater at higher temperatures. Reduced RuBisCO oxygenation reduces photorespiration at high temperatures, as represented by the temperature dependence of the photosynthetic CO2 compensation point (Γ*, equation (3)). The resulting latitudinal gradient is reproduced by both the TBMs examined (Fig. 3b) and the updated RS approaches (Fig. 3c–e). The results indicate that the influence of CO2 on photosynthesis at high latitudes is limited due to low temperatures. Estimates of the long-term change in GPP from the updated RS approaches show large changes, particularly in areas of intensive agriculture such as the midwestern United States, central and northern Europe and India (Fig. 3c,d). Compared to the RS approaches (Fig. 3d), the TBMs predict smaller increases in arid mid- and low-latitude regions, particularly in Australia and South Africa but much larger increases in the productive croplands and tropical and temperate forests (Fig. 3d). The lower TBM sensitivity, in particular of shrublands (Fig. 3f), is potentially due to poorly represented TBM processes such as the positive relationship between CO2 and woody shrub expansion29. The lower TBM sensitivities could be from inaccurate representation of greening trends that arise from changes in land management practices such as reforestation30. The relatively higher TBM sensitivity regions, particularly tropical forests (Fig. 3), may be due to insufficient TBM representation of nutrient constraints31, or the saturation of RS vegetation indices at high leaf area32, reflecting large uncertainty about the response of tropical forest photosynthesis to CO2 (ref. 33). In general, the magnitude of the TBM and updated satellite \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) suggests that the global terrestrial photosynthetic response to CO2 is consistent with the response of the light-limited photosynthetic rate which has also been suggested by observations of photosynthesis and biomass changes at the ecosystem scale34,35,36, theoretical models37,38 and by model results showing that electron-transport limited leaves are responsible for most global carbon assimilated through photosynthesis39.
a–f, The global distribution of: the sensitivity of terrestrial photosynthesis on a leaf area basis to CO2 \(({\beta }_{{\rm{R}}}^{{\rm{LUE}}})\) due to changes in LUE (a); CO2-induced changes in terrestrial photosynthesis (∆GPP, gC m−2 yr−1) from 1982 to 2012 from an ensemble of TBMs (TBMs; TRENDY-S1) (b); mean long-term changes in GPP from the two updated satellite methods, which includes a modelled direct \((\beta _{{\rm{R}}}^{{\rm{LUE}}})\) and measured indirect (\({\beta }_{{\rm{R}}}^{{\rm{fAPAR}}}\)) effect of increasing CO2 on GPP, in addition to the effect of land use and climate changes on the fraction of absorbed radiation (fAPAR) (c); the difference between the data presented in b and c (d); the latitudinal distribution of long-term changes in gross primary photosynthesis (∆GPP, PgC) from 1982 to 2012, from the TBM ensemble (orange shaded area, mean, s.d. across models) and ∆GPP predicted from RS approaches with (black, mean, s.d. between MODIS and ML approaches) and without (red) a direct effect of CO2 on LUE (Methods) (e); and long-term changes in ∆GPP, separated by plant functional types (f). EBF, evergreen broadleaved forest; SAV, savanna; DBF, deciduous broadleaved forests; CRO, croplands; SH, shrublands; ENF, evergreen needleleaf forests; GRA, grasslands; WET, wetlands.
As with any application of the emergent constraint technique, it is important to highlight that many factors could lead to biases and undermine the robustness of the derived constraint. Of primary concern is the potential for emergent constraints to rely on spurious cross-model correlations that are not based on a clear physical relationship40. The constraint we identify is based on the relationship between CO2 and the land sink, for which there is ample observational and theoretical support3,4. Although CO2 fertilization is by no means the sole likely reason for an increasing land sink4 (other contributions arise from forest regrowth, nitrogen fertilization, growing season extensions and release from cold limitations), such processes are included in the models examined and contribute to the scatter in the relationship between \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) and SLAND presented in Fig. 2a. That said, there are many processes inadequately represented in both TBMs and the satellite approaches that could lead to biases in the derived \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\). For example, models have been shown to poorly reproduce changes in the seasonal cycle of atmospheric CO2 (ref. 41) and demonstrate a range of responses when compared to results from experimental manipulation42. Nutrient limitation, thermal temperature acclimation, water stress, disturbances (including land-use change) and leaf area dynamics are all poorly represented in TBMs42,43. Future implementations of new process representations or model structures may lead to updated inference on the response of photosynthesis to CO2.
A further source of uncertainty relates to the degree of structural similarity between models and the potential for systematic cross-model biases. For example, if all models in the ensemble had the same missing or biased process representation, which led to systematic bias in the modelled relationship between the sensitivity of photosynthesis to CO2 and the land sink across models, that could bias the emergent constraint reported here. Systematic cross-model biases with shared structural similarity could also lead to an underestimation of the uncertainty associated with the values derived from the emergent constraint40,44.
The models we examine represent the state-of-the-science for land surface modelling and have substantial diversity of process representations and responses to forcings45, even for well-studied processes such as photosynthesis. Because of this diversity, there are outlier models with high or low CO2 sensitivities or SLAND estimates and such ‘wrong’ models are necessary for the formation of an emergent constraint. Indeed, removal of some outlier models, in particular CABLE and VEGAS, degrades the derived relationship between \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) and SLAND presented in Fig. 2a (to r = 0.5, 0.64; P = 0.03, 0.01, respectively) and removal of both models leads to no statistically significant relationship between \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) and SLAND (P = 0.15). If future versions of current outlier models are more consistent with the ensemble, the constraint identified here may no longer be evident.
Global photosynthesis is the largest flux of CO2 in the global carbon cycle and small changes in terrestrial photosynthesis over time can lead to large changes in the net carbon sink. The resulting feedback from the effect of increasing CO2 on photosynthesis (the carbon–concentration feedback) has been estimated to be over four times larger and more uncertain, than the direct carbon–climate feedback46. The large differences between estimates of historic changes in GPP6,7,8,9,10,15 are therefore disconcerting and could potentially lead to incorrect inference about biases in current TBMs6,14 and long-term changes in related components of the global carbon cycle such as soil respiration11,47. The confluence of approaches we use bounds the plausible range of the historic effect of CO2 on global terrestrial photosynthesis to a \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) of 0.62 ± 0.14 (mean, s.d.; Fig. 2b) and helps to reconcile differences in previous estimates. The results also show that widely used RS-based estimates of global terrestrial photosynthesis need to incorporate the effect of increasing CO2 on photosynthetic LUE and provide a globally applicable approach that is broadly consistent with the TBMs examined. Together, our results suggest that increases in atmospheric CO2 have led to a large increase in global photosynthesis since 1982, representing a strong carbon–concentration feedback that has helped to slow down the accumulation of anthropogenic emissions in the atmosphere.
Methods
The β metric of CO2 sensitivity
We quantified the apparent sensitivity of global terrestrial GPP to CO2 in the RS, TBM and independent proxy estimates using two approaches: (1) the percentage change in GPP with respect to GPP at the start of the time period (equation (5) below) and (2) a β metric defined as the response ratio (R) of GPP with respect to CO2:
where GPP(t) is the value of GPP at time t and Ca(t) is the value of atmospheric [CO2] at time t. Although other methods to calculate the β-factor have been proposed (for example, ref. 48), we use equation (1) for ease of interpretation. A β of 1 represents direct proportionality between the GPP CO2 response and the change in CO2. Note that to avoid undue influence of year-to-year variability in GPP, we estimated GPP(t) and GPP(t0) on the basis of a linear regression fit to the GPP time series.
Assessing the CO2-sensitivity of satellite-based GPP
Recent reports have highlighted that the most commonly used satellite-based estimates of GPP have a much lower CO2-sensitivity than that derived from TBMs6,11. However, most satellite-based estimates do not incorporate the universally observed direct effect of increasing CO2 on the LUE of leaves of C3 vegetation13, which is not observable from space14. The effect of increasing CO2 on global terrestrial C3 photosynthesis that we examine here manifests through two primary pathways: though increasing the biochemical rate of photosynthesis on a leaf area basis49, which we refer to as the direct effect and through increases in leaf area on a ground area basis, allowing for the interception of greater amounts of light50,51, which we refer to as the indirect effect. The former, direct response, arises because CO2 is a substrate for the photosynthetic enzyme, RuBisCO. Both CO2 and O2 compete at the active site of RuBisCO, so changes in the concentration of either affect the rate at which CO2 is assimilated, effectively changing the LUE of photosynthesis on a leaf area basis at a given light level. The latter, indirect response of increasing leaf area index (LAI51) and the resulting increase in the (fAPAR), reflects both the increased carbon available to invest in structural growth under elevated CO2 and potential changes in the hydrological equilibrium due to elevated CO2-induced increases in water-use efficiency, which can lead to increased leaf area in water-limited ecosystems52,53,54. Both response pathways are incorporated in TBMs24 and long-term proxies account for each to differing degrees. Most satellite-based estimates, however, do not account for the direct effect of increasing CO2 on the biochemical rate of photosynthesis14,55.
We assessed whether incorporating a CO2 sensitivity of LUE in RS-based approaches for estimating GPP reconciled the difference between the sensitivity of RS-based GPP to increasing CO2 and that implied by the emergent constraint. To do so, we develop a CO2 sensitivity function for incorporating the effect of increasing CO2 on the LUE of photosynthesis into satellite GPP estimates, based on the conservative assumption that the ecosystem-scale CO2 sensitivity is consistent with that of the electron-transport limited rate of photosynthesis (Aj). This is supported by reports that the observed CO2 response of photosynthesis and biomass closely corresponds to the CO2-sensitivity of Aj (ref. 35). In addition, it has been suggested that shaded, and thus primarily electron-transport limited, leaves contribute the most canopy36,56 and global terrestrial photosynthesis39. The assumption is further supported by optimal coordination theory, which posits that photosynthesis under typical daytime field conditions is close to the point where RuBisCO-limited (Ac) and Aj are colimiting. The colimitation of Ac and Aj has been shown to hold across a range of ecosystems57, as has the downregulation of the maximum velocity of carboxylation (Vcmax) under elevated CO2 to maintain coordination58. Given that the sensitivity of Aj to CO2 is much smaller than that of Ac (ref. 59), the sensitivity of Aj to CO2 therefore represents a conservative approach to incorporate a CO2 sensitivity of LUE37 in RS estimates of photosynthesis. Note that we also make the conservative assumption that C4 plants operate at or near CO2 saturation60.
The mechanistic photosynthesis model proposed by ref. 49 captures the biochemical controls of leaf photosynthesis and responses to variations in temperature, light and CO2 concentration. According to the model, the gross photosynthesis rate, A, is limited by either the capacity of the RuBisCO enzyme for the carboxylation of ribulose-1,5-bisphosphate (RuBP), the electron-transport capacity for RuBP regeneration. In the case of the limitation by the electron-transport capacity for RuBP regeneration, the photosynthetic rate (Aj, µmol m−2 s−1) is given by:
where φ0 is the intrinsic quantum efficiency, I is the absorbed light (µmol m−2 s−1), ci (Pa) is the leaf-internal CO2 concentration and Γ* (Pa) is the CO2 compensation point. Parameter Γ* depends on temperature, as estimated through a biochemical rate parameter (r)61:
where R is the molar gas constant (8.314 J mol−1 K−1), r25 = 4.22 Pa, is the photorespiratory point at 25 ˚C, ΔH is the activation energy for Γ* (37.83 kJ mol−1) and T is the temperature in K. Assuming the CO2 sensitivity of light-limited photosynthesis allows for the development of an index of the effect of CO2 on photosynthetic LUE37, which can be incorporated in any RS-based LUE model or empirical upscaling estimate of GPP.
By rewriting equation (2), substituting ci by the product of atmospheric CO2 (ca) and the ratio of leaf-internal to leaf-ambient CO2 (χ = ci/ca), the sensitivity of GPP and LUE to CO2 can be described as:
where \(\,{\phi }_{\rm{CO}_2}=\frac{{c}_{\rm{a}}\chi -{\varGamma }^{\ast }}{{c}_{\rm{a}}\chi +2{\varGamma }^{\ast }}\) and LUE = GPP/φ0I. Note that the indirect effect of CO2 on GPP through φ0I, is explicitly accounted for in satellite-based methods through changes in the fAPAR and considered here as an independent effect. However, the direct effect, through changes in LUE, (\(\phi_{{\mathrm{CO}}_2}\)), is not. We used equation (4) to derive a scalar, \(f\left({{\rm{CO}}}_{2}\right)\), to account for the direct effect of CO2 in any LUE-based estimate of GPP (for example, satellite or empirical upscaling approaches). To do so, we calculated ∆GPP in year t due to the effect of CO2 on LUE as \({\rm{GPP}}({t}=0)\times f\left({{\rm{CO}}_{2}}\right)\), where:
\(f\left({{\rm{CO}}}_{2}\right)\) thus represents the fractional increase in LUE due to the direct effect of CO2 relative to a baseline period (here 1982, the start of the time series for the satellite-based methods considered).
The sensitivity of LUE to CO2 thus depends on both Γ*, which is calculated by means of equation (3), and χ. We estimated χ using the least-cost hypothesis19,62. This states that an optimal long-term effective value of χ can be predicted as a result of plants minimizing their total carbon costs associated with photosynthetic carbon gain and explicitly expressed with the following model:
where D is vapour pressure deficit and η* is the viscosity of water relative to its value at 25 °C (ref. 63) and b is the ratio of the cost of maintaining carboxylation relative to that of maintaining transpiration19. The Michaelis–Menten coefficient of RuBisCO (K) is given by:
where Kc and Ko are the Michaelis–Menten coefficient of RuBisCO for carboxylation and oxygenation, respectively, expressed in partial pressure units and Po is the partial pressure of O2. K responds to temperature through Kc and Ko, the temperature responses for which are described using a temperature response function described by equation (3) with specific parameters: ΔH is 79.43 kJ mol−1 for Kc and 36.38 kJ mol−1 for Ko, r25 is 39.97 kPa for Kc and 27.48 kPa for Ko (ref. 61). We applied this derived sensitivity to the RS approaches detailed below, on a per-pixel basis in proportion to the percentage of C3 plants in a given pixel64, as C4 plants operate at or near CO2 saturation60. We thus make the conservative assumption of no direct CO2 effect on LUE in the C4 proportion of each pixel.
Incorporating a CO2 sensitivity into satellite-based GPP
The approach for incorporating a CO2 sensitivity we outline above (equation (5)) can be incorporated into any satellite-based photosynthesis product. Here, we test it on two broadly used approaches. The first, the MODIS MOD17 algorithm (GPPMODIS (ref. 65)) and the second an empirical upscaling method based on a model tree ensemble (GPPMTE (ref. 66)). We applied the MODIS MOD17 GPP algorithm driven by 30-year (1982–2012) Global Inventory Modeling and Mapping Studies (GIMMS3g) fAPAR data67, to calculate a new 30-year global monthly gridded (0.5°) dataset of MODIS-derived GPP:
where LUEmax represents biome-specific maximum LUE, f(D) represents a water stress reduction scalar based on the atmospheric vapour pressure deficit and \(f\left({T}_{\min }\right)\) represents a low-temperature stress reduction scalar. LUEmax, f(D) and \(f\left({T}_{\min }\right)\) are parameterized according to ref. 68. Value \(f\left({{\rm{CO}}_{2}}\right)\) is estimated on a per-pixel basis using equation (5). We used global monthly gridded (0.5°) weather data, provided by the Climate Research Unit at East Anglia University (CRU TS4.01). The total available photosynthetically active radiation (PAR) and D were calculated from insolation and CRU climate data using a simple process-based bioclimatic model (STASH69).
To incorporate a CO2 sensitivity in a global empirical upscaling dataset based on a model tree ensemble ML technique (GPPMTE, 1982–201266), which does not account for the direct effect of CO2 on LUE, we followed the approach outlined for the MODIS GPP product. Specifically, we applied the CO2 function (equation (5) to spatially distributed GPPMTE, as:
Early RS GPP models37,70 advocated for including a CO2 effect on LUE, though primarily used the larger, light-saturated, sensitivity. A recent review7 found that the most widely used modern RS GPP approaches65,66 do not include a CO2 effect on LUE and of the 3 that did (out of 14 assessed) 2 are enzyme kinetics, not LUE, models (BESS72 and BEPS70). The third (cFix71) assumes the light-saturated CO2 sensitivity, which is not suitable for global application given the large contribution of RuBP regeneration-limited leaves36,73. Some recent studies12,74,75 incorporated a CO2 effect on LUE but the approach taken typically requires the reparameterization of the LUE model and is thus not easily applicable to other RS GPP products. The approach proposed here provides a generic and conservative method for incorporating CO2 effects on LUE in any RS GPP product, which allows us to quantify the relative importance of incorporating a CO2 effect in RS GPP products and reconciles the large difference between RS and TBM-derived sensitivities to CO2.
Constraining terrestrial photosynthesis CO2 sensitivity
Emergent constraints have gained prominence in recent years as a means by which to infer unobserved quantities of interest in land surface and climate models21,22,23. The underlying core concept is that, although there is a large spread in the model estimates of an observed variable X and an unobserved variable Y across models, the relationship linking the two is sometimes tightly constrained across models. Given the existence of a strong and robust relationship across models between X and Y, observations of X can be used to generate a probabilistic inference, or constraint, on Y. This approach has been termed ‘emergent’ because the functional relationship cannot be diagnosed from a single model but rather emerges from examining the model spread21,22,23.
The emergent constraint identified in this study links the sensitivity of GPP to CO2 \(\left(\beta _{{\rm{R}}}^{{\rm{GPP}}}\right.\), see definition below) to the magnitude of the cumulative residual terrestrial sink (SLAND) between 1982 and 2016. It is derived from a linear regression across an ensemble of TBMs between the modelled cumulative SLAND and the sensitivity of GPP to CO2. We use global simulations from 15 TBMs (Supplementary Table 2) run as part of the Trends in Net Land–Atmosphere Exchange (TRENDY v.6) initiative (https://sites.exeter.ac.uk/trendy) (v.6 data are reported in ref. 76). In TRENDY, common input forcing data were prescribed for a series of model experiments from 1901 to 2015. Here we use both the results of the TRENDY v.6 scenario S3 simulations (temporally dynamic climate, CO2 and land use) as reported in the Global Carbon Project (GCP76) and the TRENDY v.6 scenario S1 simulations (CO2-only: temporally dynamic CO2, time-invariant climate; pre-industrial land-use mask). For more details on the TRENDY project see ref. 24 and for details of the TRENDY v.6 simulations used here see ref. 76.
We estimated \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) for each TRENDY v.6 TBM from annual GPP from the S1 (CO2-only) simulations, performed by 15 models (Supplementary Table 2), using equation (1) over the 1982–2012 period (to maintain consistency with the RS methods assessed). Cumulative SLAND (PgC) is calculated from the annual SLAND (PgC yr−1) reported by the GCP76 for each TRENDY v.6 TBM, which represents the annual total net biome productivity plus emissions from land-use change.
The emergent constraint approach relies on a statistical relationship between a model predicted variable for which an observational constraint exists and one for which there is no observational constraint available21,22,23. In the case of the relationship between \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) and SLAND, estimates of SLAND are made annually by the Global Carbon Project, along with the associated uncertainties25. The SLAND values we use as the constraint are the cumulative reported annual values of the residual land sink from the Global Carbon Project25 over the period from 1982 to 2016. Note that the period we used was chosen to both coincide with the satellite observations we use and to be sufficiently long so as to minimize the effect of macroclimatic events such as strong El Nino periods and volcanic eruptions.
The Global Carbon Project reports SLAND uncertainty both on an annual, decadal and a cumulative basis, with an average uncertainty of 0.9 PgC yr−1 for each of the four decades included in this study. For the 1960–2020 period where direct atmospheric CO2 measurements are available, the Global Carbon Project estimates residual land carbon uptake of 135 ± 25 GtC (mean ± s.d.; ref. 25, Table 8), with a near-zero unattributed budget imbalance. The budget closure is interpreted as evidence of a coherent community understanding of the emissions and global sinks for this period25. This provides a cumulative SLAND reference uncertainty of 18.5%, which we apply to the cumulative fluxes of the period examined (1982 to 2016). It should be noted that the uncertainty on cumulative SLAND is itself uncertain and is estimated by the Global Carbon Project based on the most up-to-date versions of the land surface models they use25. Any future reduction in cumulative SLAND uncertainty would decrease the uncertainty of \({\beta }_{{\rm{R}}}^{{\rm{GPP}}}\) reported here.
Data availability
All data used to support the findings of this study are available publicly or on request. TRENDY model simulations are available on reasonable request from TRENDY coordinator S. Sitch (s.a.sitch@exeter.ac.uk; https://globalcarbonbudgetdata.org/). The Multivariate ENSO Index is available from https://psl.noaa.gov/enso/mei/. The GIMMS fAPAR data are available on request from R. Myneni, Boston University (https://sites.bu.edu/cliveg/contact/). Climate forcings used are available from Climate Research Unit at East Anglia University (https://crudata.uea.ac.uk/cru/data/hrg/). Upscaled GPP data are available from the FluxCom initiative of the Max Planck Institute for Biogeochemistry (https://www.bgc-jena.mpg.de/geodb/projects/Home.php).
Code availability
Code used to support the findings of this study is publicly available in the GitHub repository77 at https://github.com/trevorkeenan/gpp-co2-ncc.
References
Keenan, T. F. & Williams, C. A. The terrestrial carbon sink. Annu. Rev. Environ. Resour. 43, 219–243 (2018).
Ryu, Y., Berry, J. A. & Baldocchi, D. D. What is global photosynthesis? History, uncertainties and opportunities. Remote Sens. Environ. 223, 95–114 (2019).
Walker, A. P. et al. Integrating the evidence for a terrestrial carbon sink caused by increasing atmospheric CO2. New Phytol. https://doi.org/10.1111/nph.16866 (2020).
Ruehr, S. et al. Evidence and attribution of the enhanced land carbon sink. Nat. Rev. Earth Environ. 4, 518–534 (2023).
Schimel, D., Stephens, B. B. & Fisher, J. B. Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl Acad. Sci. USA 112, 436–441 (2015).
Smith, W. K. et al. Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization. Nat. Clim. Change 6, 306–310 (2016).
Sun, Z. et al. Evaluating and comparing remote sensing terrestrial GPP models for their response to climate variability and CO2 trends. Sci. Total Environ. 668, 696–713 (2019).
Campbell, J. E. et al. Large historical growth in global terrestrial gross primary production. Nature 544, 84–87 (2017).
Ehlers, I. et al. Detecting long-term metabolic shifts using isotopomers: CO2-driven suppression of photorespiration in C3 plants over the 20th century. Proc. Natl Acad. Sci. USA https://doi.org/10.1073/pnas.1504493112 (2015).
Wenzel, S., Cox, P. M., Eyring, V. & Friedlingstein, P. Projected land photosynthesis constrained by changes in the seasonal cycle of atmospheric CO2. Nature 538, 499–501 (2016).
Li, W. et al. Recent changes in global photosynthesis and terrestrial ecosystem respiration constrained from multiple observations. Geophys. Res. Lett. 45, 1058–1068 (2018).
Chen, C., Riley, W. J., Prentice, I. C. & Keenan, T. F. CO2 fertilization of terrestrial photosynthesis inferred from site to global scales. Proc. Natl Acad. Sci. USA 119, e2115627119 (2022).
Ainsworth, E. A. & Long, S. P. What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2. New Phytol. 165, 351–372 (2005).
De Kauwe, M. G., Keenan, T. F., Medlyn, B. E., Prentice, I. C. & Terrer, C. Satellite based estimates underestimate the effect of CO2 fertilization on net primary productivity. Nat. Clim. Change 6, 892–893 (2016).
Cernusak, L. A. et al. Robust response of terrestrial plants to rising CO2. Trends Plant Sci. 24, 578–586 (2019).
Piao, S. et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Glob. Change Biol. 19, 2117–2132 (2013).
Haverd, V. et al. Higher than expected CO2 fertilization inferred from leaf to global observations. Glob. Change Biol. 26, 2390–2402 (2020).
Friedlingstein, P. et al. Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks. J. Clim. 27, 511–526 (2014).
Prentice, I. C., Dong, N., Gleason, S. M., Maire, V. & Wright, I. J. Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology. Ecol. Lett. 17, 82–91 (2014).
Keenan, T. F. et al. Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake. Nat. Commun. 7, 13428 (2016).
Eyring, V. et al. Taking climate model evaluation to the next level. Nat. Clim. Change 9, 102–110 (2019).
Winkler, A. J., Myneni, R. B. & Brovkin, V. Investigating the applicability of emergent constraints. Earth Syst. Dynam. 10, 501–523 (2019).
Hall, A., Cox, P., Huntingford, C. & Klein, S. Progressing emergent constraints on future climate change. Nat. Clim. Change 9, 269–278 (2019).
Sitch, S. et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 12, 653–679 (2015).
Friedlingstein, P. et al. Global Carbon Budget 2021. Earth Syst. Sci. Data 14, 1917–2005 (2022).
Joos, F., Meyer, R., Bruno, M. & Leuenberger, M. The variability in the carbon sinks as reconstructed for the last 1000 years. Geophys. Res. Lett. 26, 1437–1440 (1999).
Zeng, N. et al. Agricultural Green Revolution as a driver of increasing atmospheric CO2 seasonal amplitude. Nature 515, 394–397 (2014).
Long, S. P. Modification of the response of photosynthetic productivity to rising temperature by atmospheric CO2 concentrations: has its importance been underestimated? Plant Cell Environ. 14, 729–739 (1991).
Stevens, N., Lehmann, C. E. R., Murphy, B. P. & Durigan, G. Savanna woody encroachment is widespread across three continents. Glob. Change Biol. 23, 235–244 (2017).
Chen, C. et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2, 122–129 (2019).
Fleischer, K. et al. Amazon forest response to CO2 fertilization dependent on plant phosphorus acquisition. Nat. Geosci. 12, 736–741 (2019).
Myneni, R. B. et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 83, 214–231 (2002).
Cernusak, L. A. et al. Tropical forest responses to increasing atmospheric CO2: current knowledge and opportunities for future research. Funct. Plant Biol. 40, 531–551 (2013).
Ainsworth, E. A. & Rogers, A. The response of photosynthesis and stomatal conductance to rising [CO2]: mechanisms and environmental interactions. Plant Cell Environ. 30, 258–70 (2007).
Baig, S., Medlyn, B. E., Mercado, L. M. & Zaehle, S. Does the growth response of woody plants to elevated CO2 increase with temperature? A model-oriented meta-analysis. Glob. Change Biol. 21, 4303–4319 (2015).
Yang, J. et al. Low sensitivity of gross primary production to elevated CO2 in a mature eucalypt woodland. Biogeosciences 17, 265–279 (2020).
McMurtrie, R. E., Comins, H. N., Kirschbaum, M. U. F. & Wang, Y. P. Modifying existing forest growth models to take account of effects of elevated CO2. Aust. J. Bot. 40, 657–677 (1992).
Luo, Y., Sims, D. A., Thomas, R. B., Tissue, D. T. & Ball, J. T. Sensitivity of leaf photosynthesis to CO2 concentration is an invariant function for C3 plants: a test with experimental data and global applications. Glob. Biogeochem. Cycles 10, 209–222 (1996).
Li, Q. et al. Leaf area index identified as a major source of variability in modeled CO2 fertilization. Biogeosciences 15, 6909–6925 (2018).
Williamson, M. S. et al. Emergent constraints on climate sensitivities. Rev. Mod. Phys. 93, 025004 (2021).
Graven, H. D. et al. Enhanced seasonal exchange of CO2 by Northern ecosystems since 1960. Science 341, 1085–1089 (2013).
Zaehle, S. et al. Evaluation of 11 terrestrial carbon–nitrogen cycle models against observations from two temperate free-air CO2 enrichment studies. New Phytol. 202, 803–822 (2014).
De Kauwe, M. G. et al. Where does the carbon go? A model-data intercomparison of vegetation carbon allocation and turnover processes at two temperate forest free-air CO2 enrichment sites. New Phytol. 203, 883–899 (2014).
Sanderson, B. et al. On structural errors in emergent constraints. Earth Syst. Dynam. Discuss. https://doi.org/10.5194/esd-2020-85 (2021).
Fisher, J. B., Huntzinger, D. N., Schwalm, C. R. & Sitch, S. Modeling the terrestrial biosphere. Annu. Rev. Environ. Resour. 39, 91–123 (2014).
Arora, V. K. et al. Carbon–concentration and carbon–climate feedbacks in CMIP5 earth system models. J. Clim. 26, 5289–5314 (2013).
Ballantyne, A. et al. Accelerating net terrestrial carbon uptake during the warming hiatus due to reduced respiration. Nat. Clim. Change 7, 148–152 (2017).
Friedlingstein, P. et al. On the contribution of CO2 fertilization to the missing biospheric sink. Glob. Biogeochem. Cycles 9, 541–556 (1995).
Farquhar, G. D., von Caemmerer, S. & Berry, J. A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90 (1980).
Myneni, R. B., Keeling, C. D., Tucker, C. J., Asrar, G. & Nemani, R. R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 386, 698–702 (1997).
Zhu, Z. et al. Greening of the Earth and its drivers. Nat. Clim. Change 6, 791–795 (2016).
Keenan, T. F. et al. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 499, 324–327 (2013).
Donohue, R. J., Roderick, M. L., McVicar, T. R. & Farquhar, G. D. Impact of CO2 fertilization on maximum foliage cover across the globe’s warm, arid environments. Geophys. Res. Lett. 40, 3031–3035 (2013).
Ukkola, A. M. et al. Reduced streamflow in water-stressed climates consistent with CO2 effects on vegetation. Nat. Clim. Change 6, 75–78 (2016).
Smith, N. G. & Dukes, J. S. Plant respiration and photosynthesis in global-scale models: incorporating acclimation to temperature and CO2. Glob. Change Biol. 19, 45–63 (2013).
De Kauwe, M. G. et al. A test of the ‘one-point method’ for estimating maximum carboxylation capacity from field-measured, light-saturated photosynthesis. New Phytol. 210, 1130–1144 (2016).
Maire, V. et al. The coordination of leaf photosynthesis links C and N fluxes in C3 plant species. PLoS ONE 7, e38345 (2012).
Smith, N. G. & Keenan, T. F. Mechanisms underlying leaf photosynthetic acclimation to warming and elevated CO2 as inferred from least-cost optimality theory. Glob. Change Biol. https://doi.org/10.1111/gcb.15212 (2020).
Lloyd, J. & Farquhar, G. The CO2 dependence of photosynthesis, plant growth responses to elevated atmospheric CO2 concentrations and their interaction with soil nutrient status. I. General principles and forest ecosystems. Funct. Ecol. 10, 4–32 (1996).
Ehleringer, J. & Björkman, O. Quantum yields for CO2 uptake in C3 and C4 plants: dependence on temperature, CO2 and O2 concentration. Plant Physiol. 59, 86–90 (1977).
Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, A. R. Jr & Long, S. P. Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant Cell Environ. 24, 253–259 (2001).
Wang, H. et al. Towards a universal model for carbon dioxide uptake by plants. Nat. Plants 3, 734–741 (2017).
Huber, M. L. et al. New international formulation for the viscosity of H2O. J. Phys. Chem. Ref. Data 38, 101–125 (2009).
Still, C. J., Berry, J. A., Collatz, G. J. & DeFries, R. S. Global distribution of C3 and C4 vegetation: carbon cycle implications. Glob. Biogeochem. Cycles 17, 6-1-6–14 (2003).
Running, S. W. & Zhao, M. Daily GPP and Annual NPP (MOD17A2/A3) Products NASA Earth Observing System MODIS Land Algorithm—User’s Guide V3. 28 (MODIS Land Team, 2015).
Jung, M. et al. Global patterns of land–atmosphere fluxes of carbon dioxide, latent heat and sensible heat derived from eddy covariance, satellite and meteorological observations. J. Geophys. Res. https://doi.org/10.1029/2010JG001566 (2011).
Zhu, Z. et al. Global data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2. Remote Sens. 5, 927–948 (2013).
Zhao, M. & Running, S. W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 329, 940–943 (2010).
Gallego-Sala, A. et al. Bioclimatic envelope model of climate change impacts on blanket peatland distribution in Great Britain. Clim. Res. 45, 151–162 (2010).
Veroustraete, F. On the use of a simple deciduous forest model for the interpretation of climate change effects at the level of carbon dynamics. Ecol. Model. 75–76, 221–237 (1994).
Jiang, C. & Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 186, 528–547 (2016).
Zhang, S. et al. Evaluation and improvement of the daily boreal ecosystem productivity simulator in simulating gross primary productivity at 41 flux sites across Europe. Ecol. Model. 368, 205–232 (2018).
Liu, Y., Hejazi, M., Li, H., Zhang, X. & Leng, G. A hydrological emulator for global applications-HE v1.0.0. Geosci. Model Dev. 11, 1077–1092 (2018).
Yuan, W. et al. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 5, eaax1396 (2019).
Cai, W. & Prentice, I. C. Recent trends in gross primary production and their drivers: analysis and modelling at flux-site and global scales. Environ. Res. Lett. 15, 124050 (2020).
Le Quéré, C. et al. Global Carbon Budget 2017. Earth Syst. Sci. Data 10, 405–448 (2018).
Keenan, T. F. GPP-CO2: NCC paper code. GitHub github.com/trevorkeenan/gpp-co2-ncc (2023).
Acknowledgements
T.F.K. acknowledges support from NASA award 80NSSC21K1705, a US Department of Energy (DOE) ECRP Award DE-SC0021023, RUBISCO SFA DE-AC02-05CH11231 and the LEMONTREE project, funded through the generosity of E. Schmidt and W. Schmidt by recommendation of the Schmidt Futures programme. T.F.K., X.L. and Y.Z. acknowledge additional support from the NASA IDS award NNH17AE86I. M.D.K. acknowledges support from the Australian Research Council (ARC) Centre of Excellence for Climate Extremes (CE170100023), the ARC Discovery Grant (DP190101823) and the NSW Research Attraction and Acceleration Program. I.C.P. acknowledges the Imperial College initiative on Grand Challenges in Ecosystems and the Environment and the European Research Council under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement no. 787203 REALM). N.G.S. acknowledges support from Texas Tech University. B.D.S. was funded by the Swiss National Science Foundation grant no. PCEFP2_181115. C.T. was supported by a Lawrence Fellow award through Lawrence Livermore National Laboratory (LLNL), the DOE LLNL contract DE-AC52-07NA27344 and the LLNL-LDRD Program project 20-ERD-055. We thank R. Myneni and Z. Zhu for the provision of the fAPAR dataset, the Max Planck Institute for Biogeochemistry Department of Biogeochemical Integration for the provision of the upscaled GPP data. We thank the TRENDY team for the provision of the DGVM simulations and the researchers of the Global Carbon Project for making their data publicly available. We thank A. Walker for useful discussions on interpreting the deuterium isotopomer results and acknowledge the stimulating discussions during the Integrating CO2 Fertilization Evidence Streams and Theory (ICOFEST) meeting September 2018, part of the FACE model Data-Synthesis project funded by the DOE, Office of Science, Office of Biological and Environmental Research. We thank P. Friedlingstein and C. Morfopoulos for valuable input on a previous version of this paper.
Author information
Authors and Affiliations
Contributions
T.F.K. designed the study, performed the analysis and wrote the manuscript. X.L. aided in the regridding of the TRENDY model data. B.S. contributed to the emergent constraint implementation. M.D.K., B.S., I.C.P., W.H., N.S., B.M., X.L. and S.Z. provided feedback on the RS implementation. S.Z. and Y.Z. provided feedback on the emergent constraint implementation. B.S. provided feedback on the TRENDY model data interpretation. All authors discussed and commented on the results and the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Climate Change thanks Sabrina Zechlau and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Table 1
Calculation of βRGPP from existing proxies.
Supplementary Table 2
The model ensemble used TRENDY v.6, as presented in the 2017 Global Carbon Project report. Note that OCN is an additional model included in the Global Carbon Project and TRENDY v.6 but was excluded from our analysis due to the lack of S1 simulations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Keenan, T.F., Luo, X., Stocker, B.D. et al. A constraint on historic growth in global photosynthesis due to rising CO2. Nat. Clim. Chang. 13, 1376–1381 (2023). https://doi.org/10.1038/s41558-023-01867-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41558-023-01867-2