Abstract
Terrestrial ecosystems are essential for food and water security and CO2 uptake. Ecosystem function is dependent on the availability of soil moisture, yet it is unclear how climate change will alter soil moisture limitation on vegetation. Here we use an ecosystem index that distinguishes energy and water limitations in Earth system model simulations to show a widespread regime shift from energy to water limitation between 1980 and 2100. This shift is found in both space and time. While this is mainly related to a reduction in energy-limited regions associated with increasing incoming shortwave radiation, the largest shift towards water limitation is found in regions where incoming shortwave radiation increases are accompanied by soil moisture decreases. We therefore demonstrate a widespread regime shift in ecosystem function that is stronger than implied by individual trends in incoming shortwave radiation, soil moisture and terrestrial evaporation, with important implications for future ecosystem services.
Similar content being viewed by others
Main
The provision of food and water, the uptake of CO2 and evaporative cooling depend on a sufficient moisture supply to the land surface1,2. Climate change affects moisture supply and, in combination with rising atmospheric CO2, affects ecosystem function3,4,5,6,7,8. The water and carbon cycles are coupled via vegetation, which assimilates CO2 during photosynthesis, while simultaneously transpiring through the stomata. From an energy balance perspective, transpiration (T) cools the surface air at the expense of energy which would otherwise contribute to surface heating9,10,11. Through this water–vegetation–climate feedback, changes in soil moisture influence evaporative cooling and consequently surface warming10. However, regional changes in water availability do not affect ecosystem function uniformly. Ecosystem responses depend on whether the region is energy limited or water limited5,12,13,14. In addition, rising atmospheric CO2 is expected to influence physiological processes that create more favourable conditions for photosynthesis and consequently plant growth15,16,17 with contrasting impacts on plant transpiration and therefore energy and water cycles15,16.
Fundamental to the future of the terrestrial carbon sink is the extent to which terrestrial ecosystems are becoming more water limited3,4,18,19,20,21,22,23,24. Agreement in trends of individual water-related variables such as soil moisture and terrestrial evaporation (usually referred to as evapotranspiration25) is lacking. This extends to traditional drought or aridity indices, irrespective of whether observations22,26,27,28, reanalyses28, climate model simulations28,29 or future climate projections22,30,31,32,33,34 are used. The analysis of the ecosystem response to a changing climate is complicated by various processes involved at different temporal scales and operating in different directions. For instance, while the observed widespread vegetation greening in recent decades does not support the notion of increased water limitation15,16,17,19, it is mostly driven by CO2 fertilization which can, at least temporarily, overshadow ongoing changes in water availability. Further, by controlling water availability in water-limited regions, large-scale modes of variability (for example, the El Niño/Southern Oscillation) exert strong controls over interannual variability in ecosystem water limitation35. Reconciling the degree to which ecosystem water limitation can affect vegetation through drought stress36 and tree mortality37 and lead to changes in surface properties including albedo38,39 and roughness40 is crucial. Existing uncertainty is partly related to differing approaches30. Some studies analysed water supply through soil moisture3,4,18,23,24, others focused on water demand by considering precipitation alongside (potential) evaporation19,21,22. These differing approaches can lead to different outcomes41.
In contrast to the debate on water availability, increasing trends in energy availability are clear, consistent and coincide with increasing temperatures42. This affects ecosystems in multiple ways; the RuBisCO enzyme activity is crucial for photosynthesis and is sensitive to increasing temperatures43,44. Further, temperature influences vapour pressure deficit34,45,46; higher temperatures increase atmospheric evaporative demand, increasing ecosystem water limitation and, potentially, cause plants to close their stomata to prevent excessive water loss47,48,49. This highlights the necessity of considering energy and water variables together in a comprehensive characterization of ecosystem water limitation3,45.
Here we study ecosystem energy limitation and water limitation together, to reconcile whether the surface is drying or wetting from an ecosystem function perspective. We use the ecosystem limitation index (ELI12; Methods) that reflects the fundamental concepts of water limitation and energy limitation. These typically focus on the sensitivity of ecosystem function (represented through terrestrial evaporation anomalies) to water (soil moisture anomalies) and energy availability (incoming shortwave radiation anomalies). Here these sensitivities are assessed statistically with correlations between anomalies of terrestrial evaporation with soil moisture (cor(SM′,ET′), typically positive in water-limited conditions) and incoming shortwave radiation (cor(SWin,ET′), typically positive in energy-limited conditions12,50), respectively. The ELI is then computed as cor(SM′,ET′) − cor(SWin,ET′), where the prime denotes monthly anomalies of soil moisture (SM), terrestrial evaporation (ET) and incoming shortwave radiation (SWin), respectively. Positive ELI values denote water-limited conditions and negative values indicate energy-limited conditions. This way, the ELI moves beyond traditional drought indices based on meteorological information by evaluating the functional ecosystem response to hydrometeorological conditions. Further, the ELI permits studying deviations from the seasonal cycle by using monthly anomalies. Within the ELI, the terrestrial evaporation reflects the total ecosystem response, as it comprises bare soil evaporation, canopy interception and plant transpiration. Soil moisture is used as it reflects water available for terrestrial evaporation. Incoming shortwave radiation functions as the main proxy for energy availability, as it is directly used by plants for photosynthesis and can therefore be closely associated with plant transpiration. As such, it has widely been used as an energy proxy for ET51. In addition to incoming shortwave radiation, we use air temperature as a simple and widely available proxy for energy availability. The ELI is calculated using historical and ‘worst-case’ Shared Socioeconomic Pathway (SSP) 5-8.5 simulations from the Coupled Model Intercomparison Project Phase 6 (CMIP6; ref. 52) from 11 models (Methods) for the period 1980–2100.
Continuation of present ecosystem limitation trends
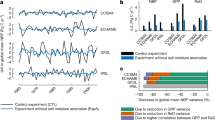
We find a steady increase in ELI throughout 1980–2100, mainly reflecting a weakening correlation between terrestrial evaporation anomalies and incoming shortwave radiation anomalies but also a strengthening correlation with soil moisture anomalies (Fig. 1a). A comparable ELI trend can be found when computed with anomalies of air temperature as an alternative energy variable (Supplementary Fig. 1), due to high correlation of incoming shortwave radiation and air temperature at the monthly time scale. A similar agreement between ELI trends from different models can be found when exchanging time on the x axis for air temperature warming since 1980 (Supplementary Fig. 2), pointing to similar climate sensitivities between these models. This comparison also indicates that beyond a global warming of 1.5 °C, all considered models agree on the increasing sign of the ELI change. The relatively small change in water limitation corroborates the projections of hardly any dryland expansion as previously reported18. However, despite a larger contribution of energy limitation, the strong ELI trend is a result of contributions of both components.
a–e, Global evolution of ELI and its individual components cor(SM′,ET′) and cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) and related variables (a), \({\rm{SW}}_{\rm{in}}\) (divided by the latent heat of vaporization and assuming a density of 1,000 kg m−3) (b), SM (c), ET (d), LAI (e) and aridity index (f). Dashed coloured lines depict the globally and decadally averaged time series of all respective variables per individual model. Solid lines with dots depict multimodel mean time series inferred from the model-specific time series (the median is used in f, as aridity index can approach infinity in regions with low precipitation), where the shaded regions cover ±1 multimodel standard deviation. The y axis denotes the change since 1980 onward. Global averages are calculated over land grid cells that have complete time series for all models and variables and are weighted according to the surface area per grid cell. Dot-dashed lines in d denote reference terrestrial evaporation datasets23,28,29,72. This figure is created with the ggplot2 package73.
We find that the role of incoming shortwave radiation versus soil moisture is more pronounced when comparing their respective global trends (Fig. 1b,c). Widespread increasing incoming shortwave radiation is associated with declining energy limitation, thereby increasing the ELI. Simultaneously, this involves increasing atmospheric water demand associated with higher temperatures (Supplementary Fig. 3c), as reflected in variables such as relative humidity or vapour pressure deficit (Supplementary Fig. 3a,b; refs. 33,45,46). This further increases ecosystem water limitation and consequently temperature through the water–vegetation–climate feedback. In contrast to multimodel incoming shortwave radiation trends, global changes in soil moisture are not substantial (Fig. 1c), with substantial uncertainty across models. This uncertainty is related to inconclusive trends in precipitation (ref. 53; Supplementary Fig. 3d) and land surface dryness, which varies between regions and soil depths54 and differences between root-zone depths amongst the models.
Until approximately 2030 the CMIP6 models agree on a global terrestrial evaporation increase (Fig. 1d). From 2030 onwards, multimodel uncertainty increases substantially, as some models show continued increases in terrestrial evaporation, while others suggest decreases. The increase in uncertainty of terrestrial evaporation trends over time is also apparent for precipitation (Supplementary Fig. 3d), which leads to a net zero change in water storage in the root zone with increasing uncertainties (Fig. 1c). The sign and magnitude of global multimodel terrestrial evaporation trends compare well with a sample of state-of-the-art datasets, suggesting that CMIP6 models represent terrestrial evaporation reasonably and that terrestrial evaporation from these models can be used to evaluate changes in land–atmosphere interactions.
The consistent increase of leaf area index (LAI) during the study period, with increasing multimodel spread, reflects the impact of CO2 fertilization15,16,17,55. Enhanced LAI in turn contributes to increased plant transpiration (Supplementary Fig. 4c; ref. 56). Combined with the levelling off of increases in the multimodel mean of the sum of bare soil evaporation and canopy interception around 2030 (Supplementary Fig. 4b), the fraction of transpiration with regards to terrestrial evaporation increases in the future too (T/ET; Supplementary Fig. 4a,c,d). This suggests an increasing influence of vegetation for the land water and energy balances. Additionally, when only considering plant transpiration anomalies for ELI (ELIT) instead of terrestrial evaporation anomalies (default ELI), we find a similar but slightly weaker signal (Supplementary Fig. 5). While energy limitation in ELI and ELIT are very similar, water limitation is stronger in ELI, which corroborates earlier findings57. This is not solely due to plant transpiration relying mostly on root-zone soil moisture with large uncertainties (Fig. 1c) but also to plant transpiration being parametrized differently by models and it being probably more uncertain than terrestrial evaporation due to a lack of observations56. The higher values for cor(SM′,ET′) can be related to, and confounded by, canopy interception, as precipitation evaporates from leaves instead of infiltrating into the root zone57. In this context, we use partial correlations cor(SM′,ET′|\({\rm{SW}}_{\rm{in}}^{\prime}\)) and cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′|SM′) for computing an alternative ELI to exclude confounding effects of energy on water limitation and vice versa and show that the ELI trend remains similar but slightly weaker (Supplementary Fig. 6). This is similar to earlier observation-based findings in Europe12. Pure water limitation is more sensitive to confounding energy effects than vice versa, due to the globally consistent incoming shortwave radiation trend (Fig. 1b) as opposed to the more uncertain global soil moisture trend (Fig. 1c).
Finally, the long-term land surface dryness as expressed by the multimodel mean aridity index (unit-normalized net radiation divided by precipitation) tends to increase (Fig. 1f) but less consistently than the ELI. This (1) suggests that the ELI trend cannot be explained without considering those ecosystem feedbacks that amplify water limitation and (2) shows the importance of comprehensively analysing regime shifts from an ecosystem perspective. Further, we compare the trends across all considered variables that are normalized by the interannual standard deviation of the respective detrended time series (Supplementary Fig. 7). Here the normalized ELI trend is most notable, even more than its individual components. This underlines the importance of the combined effect of changes in energy and water availability alongside respective ecosystem feedbacks. We note that the uncertainties shown for the trends of incoming shortwave radiation, terrestrial evaporation and particularly soil moisture do not directly affect the estimation of the ELI. The ELI is computed from detrended and de-seasonalized data (Methods) where this preprocessing is done separately for each model and grid cell such that different trends and seasonal cycles are removed. The remaining uncertainty between the (interplay) of the anomalies induces the observed intermodel spread in the estimation of the ELI as shown in Fig. 1a; however, this only concerns the magnitude of the increasing ELI trend, not the trend itself which is apparent from all individual models.
Expansion of ecosystem water limitation
As shown in Fig. 2a, we find increasing ELI trends across ~73% of the warm land area (all grid cells with a sufficient number of months with air temperature Ta > 10 ˚C in at least four models; Methods). Positive ELI trends are more widespread than negative trends: P < 0.05 in 36% of the warm land area for positive trends in contrast to 5% for negative trends. We defined regions of interest (dashed boxes) around those areas with the strongest ELI trends: North America (NAM), South America (SAM), Central Europe (CEU), Northern Eurasia (NEU) and East Asia (EAS). As shown in the inset of Fig. 2a, ELI increases tend to be strongest over regions with large tree coverage. The increasing drought stress, particularly in these regions in northern latitudes, has substantial implications for the magnitude, and potentially sign, of CO2 exchange6,58. The ELI trends of the individual CMIP6 models show similar spatial patterns (Supplementary Fig. 8) and agree well with the sign of the multimodel mean ELI trend (Supplementary Fig. 9a), particularly in the regions of interest. This agreement between individual CMIP6 models emerges despite the relatively high standard deviation between trends of individual CMIP6 models in the regions of interest (Supplementary Fig. 9b), illustrating that CMIP6 models generally agree on the sign of the ELI trend but less on the magnitude. Elaborating further on the individual contributions of water limitation and energy limitation on regional ecosystem regime shifts (Fig. 1), we show that, particularly in the regions of interest, the ELI trend is driven by both an increasing water limitation and a decreasing energy limitation (Supplementary Fig. 10).
a, Trend in the multimodel mean of ELI (dots indicate significance: P < 0.05 based on Kendall’s tau statistic). The dashed boxes indicate regions of interest to aid easier cross-comparisons with other maps. The top inset displays the fraction of the warm land area that is drying or wettening according to ELI trends (P < 0.05 is hued darker). The bottom inset displays area-weighted average ELI trends for regions with different tree fractions based on six CMIP6 models (Methods). b, Multimodel mean ELI between 1980 and 2100. c, Same as b but derived with air temperature (Ta) instead of incoming shortwave radiation anomalies. d, Timing of regime shift from energy limitation to water limitation as indicated by ELI values becoming positive. The inset shows the global time series of the water-limited fraction of the warm land area (Methods). This figure is created with the ggplot2 package and the country borders using the maptools package73,74.
Figure 2b shows that in the regions of interest, current conditions are either slightly energy limited or transitional, hinting at an expansion of water-limited area from 1980 to 2100. We also observe further shifts towards ecosystem water limitation in current water-limited regions, such as parts of South America, North Africa, Australia and the west of North America. Interestingly, not all tropical regions are consistently subjected to increasing ELI. For example, there is a contrast between South America and tropical Africa because soil moisture is decreasing across large parts of South America (Supplementary Fig. 11b), while for Central Africa the CMIP5 ensemble estimates increasing soil moistures related to projected precipitation increases59. Spatial patterns of ELI (trends) computed with air temperature anomalies are comparable (Fig. 2c), with SAM and Central Africa being slightly less energy limited. This indicates a higher sensitivity of tropical ecosystems to incoming radiation due to typically dense cloud cover making radiation a limiting factor for terrestrial evaporation (Supplementary Fig. 10b)60.
Next, we assess the timing of shifts of energy- to water-limited regions over the study period (Fig. 2c). We detect the time of regime shifts as the first decade after which the ELI is of positive sign. We find that transitional regions are migrating in space throughout 1980–2100, most notably in the Northern Hemisphere (NAM and NEA). This causes the water-limited fraction of the warm land area to expand from 70% to 77% (inset), representing approximately an additional 7 million km2 in 2100 as compared to 1980. ELI increases occur continuously over time and in similar ways across different regions of interest (Supplementary Fig. 12). This foreshadows a further expansion of areas in water deficit, continuing an observed trend over 1982–20154. Further, this indicates that global ELI trends (Figs. 1a and 2a) are not simply strengthening (weakening) pre-existing water-limited (energy-limited) conditions but lead to actual regime shifts. We find similar ELI trends when applying air temperature anomalies as a proxy for energy availability (Supplementary Fig. 13a) but since especially the tropics show a lower sensitivity to temperature anomalies, spatial shifts in the transitional regions are particularly different in SAM (Supplementary Fig. 13b).
In addition to assessing ELI trends in space, we show trends in water-limited months-of-year to investigate ELI changes in time across seasons (Fig. 3). In 43% of the warm land area, and particularly in our regions of interest, we detect an increase in the duration of the water-limited season by up to 6 months, as opposed to a decrease in water-limited months in 3% of the warm land area. The side panels in Fig. 3 show the changes over time in the duration of the water-limited season. For NAM, NEA, CEU and EAS the warm season length (months-of-year with temperature >10 ˚C) increases, while in SAM it already covers all months. In all regions, the water-limited season expands to earlier and/or later months which were previously energy-limited or cold. Further, the maximum water limitation intensifies.
The central panel displays trends of the number of water-limited months-of-year expressed as Theil–Sen slope across decades (dots indicate significance: P < 0.05 based on Kendall’s tau statistic; Methods). Grey denotes regions where no significant changes in the length of the water-limited season were detected. Side panels show the multimodel mean month-of-year ELI evolution in the regions of interest (Methods). White colour denotes cold months (Ta < 10 °C). This figure is created with the ggplot2 package and the country borders using the maptools package73,74.
Attribution of trends towards ecosystem water limitation
Attributing ELI trends to land–atmosphere variables, in Fig. 4 we identify relevant variables in ~59% of the warm land area, where sufficient variance of the ELI time series (12 decadal values) can be explained by the optimal combination of hydrological, meteorological and ecological predictors. Figure 4 does not necessarily rely on one multiple linear model only; all possible combinations of predictors are attempted and we consider all similarly performing multiple linear models (adjusted R2 > 0.5; Methods). By doing so, we effectively exclude predictors that carry similar information, which means that if multiple predictors are included in the best model, they must carry different information about ELI variability. Incoming shortwave radiation is the most important ELI predictor and is dominant in 20% of the warm land area. The other predictors are less dominant (9–11% of the warm land). Clearly, incoming shortwave radiation is relatively most important in terms of the area where it can predict ELI trends but the full set of variables is required to explain the trends globally as evidenced by the few grid cells that only have one predictor, which confirms earlier attribution analyses based on observations and model simulations4,48. Similar results are obtained with different thresholds for model performance (adjusted R2 > 0.3 or adjusted R2 > 0.7; Supplementary Fig. 14).
Colours indicate the variables that best predict the decadal ELI dynamics calculated using multivariate linear regression with a set of equally well-performing models, across which the most meaningful predictor is selected (Methods). Stippling indicates grid cells where only one linear model performs well (adjusted R2 > 0.5) and contains only a single explanatory variable. Grey colour denotes grid cells without any model with reliable performance (adjusted R2 < 0.5). Insets show the total fraction of warm land area controlled by respective variables (top) and the fraction of ELI trends controlled by incoming shortwave radiation per region of interest (bottom). This figure is created with the ggplot2 package and the country borders using the maptools package73,74.
The scattered pattern in Fig. 4 underlines the relevance of local climate, vegetation and/or soil characteristics and, by extension, land use changes in inducing shifts in ELI. We therefore extend the analysis in Fig. 4, by expanding the number of considered predictors in the multivariate linear regression by including the time series of crop and tree fraction as proxies for land use change (Supplementary Fig. 15). The importances of changes in crop and tree fraction does not exceed the other variables. Moreover, the global average adjusted R2 across the considered well-performing multivariate linear models in all grid cells is similar (0.42 versus 0.43 in the default analysis), indicating that the additional predictors are not important at the large spatial scales investigated here. Finally, the robustness of the multimodel mean attribution analysis is further confirmed by shortwave incoming radiation emerging as the most important predictor for most of the individual Earth system models (Supplementary Fig. 16).
Across the regions of interest, incoming shortwave radiation is the most relevant predictor in 27%–57% of the respective regional areas where well-performing linear models could be fitted. Incoming shortwave radiation is the most important predictor across most regions of interest, apart from CEU (Supplementary Fig. 17). This is corroborating the widespread alleviating energy limitation pushing ecosystems towards water limitation (Fig. 1a and Supplementary Fig. 10b). The trends in the individual variables confirm that within the regions of interest, both increasing incoming shortwave radiation and decreasing soil moisture contribute to increasing ecosystem water limitation (Supplementary Fig. 11). In addition, increasing CO2 and favourable energy availability and water availability cause plants to increase their LAI and consequently terrestrial evaporation rates. LAI is increasing in regions close to transitioning between water- and energy-limited conditions and particularly at the northern latitudes: plants may compete for light when water is abundant (and light is limiting) by allocating part of the increased carbon uptake to growing more leaves61.
While our study presents clear evidence of globally increasing ELI and physical mechanisms behind the changes, the accuracy of the analyses is intrinsically limited due to inherent uncertainties in the models. For example, different representations of some processes that are relevant for ecosystem function cause uncertainty in CMIP6 model simulations including the expected effects of CO2 fertilization on LAI17,55, water use efficiency15,16 and the implementation of dynamic vegetation (Methods). Some models have also been shown to be oversensitive to CO2 fertilization62. Other processes, such as the development of deeper roots in response to increased water (or nutrient) demands63,64, are typically not represented. Further, models have difficulty capturing evaporative regime changes65,66,67 which can arise from different representations within the complex coupled land–atmosphere system. This affects the multimodel spread, with respect to both the ELI trends and means that are largest in the regions of interest (Supplementary Fig. 7). Finally, next to energy limitation and water limitation, nutrient limitation on plant transpiration potentially plays an increasingly important role in the future68. We do not consider nutrient limitation; it is difficult to validate models given the sparsely available observational data and uncertainties associated with human involvement in the phosphorus and nitrogen cycles69. Despite these shortcomings, the multimodel mean terrestrial evaporation closely resembles state-of-the-art datasets. We suggest that these uncertainties may influence the magnitude but not the sign of ELI trends (Supplementary Fig. 9). Finally, we have established the ability of the ELI to reflect spatiotemporal variability in water-limited conditions by using a conceptual soil moisture model within which the concept of water limitation is implemented through a soil moisture stress function. Using model output, we successfully validate the ELI against the number of days that soil moisture is drier than the critical soil moisture, effectively reflecting water-limited conditions, in a number of grid cells spanning from energy- to water-limited conditions (Supplementary Discussion and Supplementary Fig. 20).
Our study reveals a widespread regime shift from ecosystem energy limitation to water limitation that can be attributed to a large extent to global warming. The strongest regional ELI trends are attributed to a combination of reduced energy limitation and exacerbated water limitation. Moreover, we find that incoming shortwave radiation is the most important predictor for the trend towards ecosystem water limitation but not exclusively so as global patterns can only be explained using a wider range of variables, including soil moisture, terrestrial evaporation, LAI and aridity index.
The ongoing debate on the importance of energy limitation versus water limitation for terrestrial evaporation and ecosystem productivity3,23,48,70,71 can therefore be resolved by simultaneously considering energy- and water-limitation trends for ecosystem function. While, globally, soil moisture is important for making ecosystems water- or energy-limited9,10,12, incoming shortwave radiation trends prove more consistent and dominate trends in ecosystem function.
Our analysis demonstrates a globally increasing ecosystem water limitation over 73% of the warm land area. This has implications for food and water scarcity, land degradation, disruption of CO2 sequestration by terrestrial ecosystems, reduction in biodiversity and the duration, intensity and frequency of extreme events. By simultaneously considering both energy limitation and water limitation, a fuller explanation of regional changes in ecosystem function and a clearer view of future changes in these systems can be obtained.
Methods
Ecosystem limitation index
The ELI is based on the correlation-difference index introduced by ref. 12:
Kendall’s rank correlation is used to avoid assuming linear relationships between variables and prime denotes monthly anomalies of SM, ET and SWin, respectively, which are derived by removing long-term trends and mean seasonal cycles (section on ‘Data preprocessing’). We use monthly time resolution to mitigate the influence of synoptic weather variability. The ELI combines information on water (cor(SM′,ET′)) and energy availability (cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′)) for a considerate estimate of ecosystem function. The choices of the variables representing energy (incoming shortwave radiation) and water availability (soil moisture) and ecosystem function (terrestrial evaporation) are explained in the introduction.
The purpose of ELI is to distinguish water- and energy-limited regimes (Supplementary Table 1). With the soil moisture content below the wilting point (SMwilt), no water can be extracted from the soil for evaporation, neither for plant transpiration nor bare soil evaporation. The associated extremely low variability in terrestrial evaporation leads to near-zero cor(SM′,ET′), cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) and ELI.
In water-limited regions, typically ELI > 0, cor(SM′,ET′) > 0 and cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) is either close to zero or negative. In these regions, the soil moisture is typically between the wilting point and the critical soil moisture content (SMcrit), which is defined as the soil moisture content above which plants can sustain their maximum evaporative fraction9,10,11. So when SMwilt < SM < SMcrit, positive soil moisture anomalies tend to increase the terrestrial evaporation, while negative soil moisture anomalies achieve the contrary (cor(SM′,ET′) > 0). Further, a positive soil moisture anomaly arises from precipitation; in addition, the related cloudiness prevents radiation from reaching the land surface, which leads to a negative incoming shortwave radiation anomaly (cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) < 0).
In energy-limited conditions, typically ELI < 0, cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) > 0 and cor(SM′,ET′) is either close to zero or negative. When the soil moisture content exceeds the critical soil moisture, the maximum evaporative fraction can be sustained and any soil moisture anomaly will not affect terrestrial evaporation directly (cor(SM′,ET′) ≈ 0). Next to water, ample energy should be available in the form of adequate incoming shortwave radiation. Therefore, any positive (negative) incoming shortwave radiation anomalies will increase (decrease) terrestrial evaporation cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) > 0.
Supplementary Table 1 explains that, according to average soil moisture conditions, soil moisture anomalies play an obvious role for terrestrial evaporation. But, in energy limitation, incoming shortwave radiation anomalies dictate terrestrial evaporation. Therefore, it is important to consider energy availability cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) alongside water availability cor(SM′,ET′) when assessing ecosystem function. Note that the ELI is a correlative index, which cannot prove causality.
The different combinations of individual correlations in Supplementary Table 2 reveal characteristic local temporal dynamics that could lead to either general energy limitation (ELI < 0) or water limitation (ELI > 0). For example, water limitation is concluded when ELI > 0, which follows when cor(SM′,ET′) > cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′) is satisfied. The opposite is true for energy-limited conditions: when ELI < 0, cor(SM′,ET′) < cor(\({\rm{SW}}_{\rm{in}}^{\prime}\),ET′). Supplementary Table 2, which summarizes the most common combinations of the individual correlations to conclude water-limited (ELI > 0) or energy-limited conditions (ELI < 0), shows that the most common combination across all models and decades (section on ‘Data preprocessing’) is when both individual correlations are of opposing sign (84% of the water-limited warm land area and 58% for energy limitation), indicating that almost, if not all, months in that respective decade are consistently water- or energy-limited. Positive correlations of the same sign indicate that that decade is characterized by both intermittent energy- and water-limitation. Slightly negative individual correlations might co-occur but are usually insignificant and are therefore excluded.
CMIP6 data
We use publicly available simulations from 11 models included in CMIP6 (ref. 52), of which the most important aspects are summarized in Supplementary Table 3. For the historical period, we use the model simulations from 1980 to 2015. From the future scenario (2015–2100), we use simulations from the ‘worst-case’ SSP 5-8.5 scenario from ScenarioMIP75, which combines the 2100 forcing level of 8.5 W m−2 of the CMIP5 Representative Concentration Pathways simulations (RCP 8.5) with newly defined SSP simulations for fossil-fuelled development (SSP 5). We do so assuming that this worst-case scenario will give insight into the potential implications on ecosystem function. All data are downloaded at the monthly time scale and aggregated to a common 2 × 2 degree grid cell spatial resolution.
Data preprocessing
After acquiring the data, a series of steps is taken to compute the ELI from the raw time series of the respective variables, which we have illustrated for two typically water- and energy-limited grid cells, respectively (Supplementary Figs. 18 and 19). Per individual CMIP6 model, the entire 120-yr period is divided into 12 decades (top row). Detrending is done per decade by removing linear regression fits (left panel, middle row), to minimize biases in the anomaly estimation that relate to assuming trend linearity over the entire 120-yr period. In addition, the seasonal cycle is calculated per decade as the month-of-year average of the respective variable (middle panel, middle row). The anomalies result from subtracting the seasonal cycle from the detrended time series (right panel, middle row). From the resulting time series we exclude all months colder than 10 ˚C to remove periods with presumably inactive or sparse vegetation and frozen soils (dashed lines, right panel, middle row), at the same time ensuring that there is sufficient variability in terrestrial evaporation for computing the correlations that constitute the ELI. Thereafter, we compute the ELI for each decade and model. Thereby, we ignore grid cells with <30 data points. Whereas we use model data in this analysis to study potential long-term shifts in ecosystem water limitation, we highlight that this methodology can also be used in near-real time to monitor climate change in observational data with a trailing period of a decade. In addition, trends could be obtained by applying a moving window of a decade.
The warm land area as referred to in the manuscript then constitutes all grid cells that have full ELI time series from 1980–2100 for at least four models. The decadal month-of-year ELI time series (Fig. 3) are only calculated when in the respective decade and month-of-year all ten data points are available (temperature is warmer than 10 °C).
The saturated vapour pressure was calculated with temperature and relative humidity as:
where Ta is air temperature in ˚C. Then, the vapour pressure deficit (VPD) is:
where RH is the relative humidity.
The sum of bare soil evaporation and canopy interception was calculated by subtracting plant transpiration from terrestrial evaporation (ET − T).
Computing Theil–Sen slopes and slope significance
The trends shown in Figs. 2 and 3 and Supplementary Figs. 8, 10, 11 and 13 are based on Theil–Sen slopes76,77. This approach is insensitive to statistical outliers, as the median slope from a range of possible slopes is selected as the best fit. The significance of these slopes is determined on the basis of Kendall’s tau statistic from Mann–Kendall tests.
Multimodel inference using the Akaike Information Criteria
We assess the skill of a range of predictors (Supplementary Table 4) to predict decadal ELI time series by using multivariate linear regression in combination with the dredge function in the MuMin package in R78,79, thereby adopting a similar methodology to ref. 80. This function tries all possible combinations of predictors and ranks them on the basis of Akaike Information Criterion (AIC), allowing the selection of a range of similarly well-performing multivariate linear models with respect to model performance (likelihood) and complexity (number of parameters). From this, we select all models whose difference in AIC with the best-ranked model is smaller than 4, which results in 1 to a maximum of 15 similarly performing multivariate linear models per grid cell. Only multivariate linear models with sufficient predictive power (adjusted R2 > 0.5) are considered in the attribution analysis. In the case that there is only one model with one explanatory variable, this is assumed the most important predictor in that respective grid cell. Given just one multivariate linear model with multiple predictors, the most important variable is determined according to the variance explained per variable according to the ‘lmg’ metric in the ‘relaimpo’ R package81. When there are multiple multivariate linear models with multiple predictors, the most important predictor is picked according to the average variance explained across all multiple linear models, weighted by the Akaike weights assigned to all models.
Data availability
The CMIP6 model simulations are freely available from Google cloud CMIP6 public data: https://pangeo-data.github.io/pangeo-cmip6-cloud/. All the data used in this analysis are publicly available from a data repository that can be accessed via Zenodo: https://doi.org/10.5281/zenodo.6566274.
Code availability
The scripts to acquire and aggregate CMIP6 data are publicly available and can be accessed via Zenodo: https://doi.org/10.5281/zenodo.5900392. All the code used for this analysis are publicly available from a code repository which can be accessed via Zenodo: https://doi.org/10.5281/zenodo.6566648.
Change history
16 June 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41558-023-01729-x
References
Mekonnen, M. M. & Hoekstra, A. Y. Four billion people facing severe water scarcity. Sci. Adv. 2, e1500323 (2016).
Piao, S. et al. The impacts of climate change on water resources and agriculture in China. Nature 467, 43–51 (2010).
Green, J. K. et al. Large influence of soil moisture on long-term terrestrial carbon uptake. Nature 565, 476–479 (2019).
Jiao, W. et al. Observed increasing water constraint on vegetation growth over the last three decades. Nat. Commun. 12, 3777 (2021).
Ciais, P. et al. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 437, 529–533 (2005).
Gampe, D. et al. Increasing impact of warm droughts on northern ecosystem productivity over recent decades. Nat. Clim. Change 11, 772–779 (2021).
Reichstein, M. et al. Climate extremes and the carbon cycle. Nature 500, 287–295 (2013).
Rockström, J. et al. Future water availability for global food production: the potential of green water for increasing resilience to global change. Water Resour. Res. 45, W00A12 (2009).
Budyko, M. I. Climate and Life (Academic Press, 1974).
Seneviratne, S. I. et al. Investigating soil moisture–climate interactions in a changing climate: a review. Earth-Sci. Rev. 99, 125–161 (2010).
Denissen, J. M. C. et al. Soil moisture signature in global weather balloon soundings. npj Clim. Atmos. Sci. 4, 1–8 (2021).
Denissen, J. M. C., Teuling, A. J., Reichstein, M. & Orth, R. Critical soil moisture derived from satellite observations over Europe. J. Geophys. Res. Atmos. 125, e2019JD031672 (2020).
Flach, M. et al. Contrasting biosphere responses to hydrometeorological extremes: revisiting the 2010 western Russian heatwave. Biogeosciences 15, 6067–6085 (2018).
Kroll, J. et al. Spatially varying relevance of hydrometeorological hazards for vegetation productivity extremes. Biogeosciences 19, 477–489 (2022).
Donohue, R. J., Roderick, M. L., McVicar, T. R. & Farquhar, G. D. Impact of CO2 fertilization on maximum foliage cover across the globe’s warm, arid environments. Geophys. Res. Lett. 40, 3031–3035 (2013).
Ukkola, A. M. et al. Reduced streamflow in water-stressed climates consistent with CO2 effects on vegetation. Nat. Clim. Change 6, 75–78 (2016).
Zhu, Z. et al. Greening of the Earth and its drivers. Nat. Clim. Change 6, 791–795 (2016).
Berg, A. & McColl, K. A. No projected global drylands expansion under greenhouse warming. Nat. Clim. Change 11, 331–337 (2021).
Berg, A. & Sheffield, J. Evapotranspiration partitioning in CMIP5 models: uncertainties and future projections. J. Clim. 32, 2653–2671 (2019).
Greve, P. et al. Global assessment of trends in wetting and drying over land. Nat. Geosci. 7, 716–721 (2014).
Feng, S. & Fu, Q. Expansion of global drylands under a warming climate. Atmos. Chem. Phys. 13, 10081–10094 (2013).
Huang, J., Yu, H., Guan, X., Wang, G. & Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Change 6, 166–171 (2016).
Jung, M. et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467, 951–954 (2010).
Zhou, S. et al. Soil moisture–atmosphere feedbacks mitigate declining water availability in drylands. Nat. Clim. Change 11, 38–44 (2021).
Miralles, D. G., Brutsaert, W., Dolman, A. J. & Gash, J. H. On the use of the term “Evapotranspiration”. Water Resour. Res. 56, e2020WR028055 (2020).
Albergel, C. et al. Monitoring multi-decadal satellite earth observation of soil moisture products through land surface reanalyses. Remote Sens. Environ. 138, 77–89 (2013).
Dorigo, W. et al. Evaluating global trends (1988–2010) in harmonized multi-satellite surface soil moisture. Geophys. Res. Lett. 39, L18405 (2012).
Mueller, B. et al. Benchmark products for land evapotranspiration: LandFlux-EVAL multi-data set synthesis. Hydrol. Earth Syst. Sci. 17, 3707–3720 (2013).
Zhang, Y. et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 6, 19124 (2016).
Berg, A. & Sheffield, J. Climate change and drought: the soil moisture perspective. Curr. Clim. Change Rep. 4, 180–191 (2018).
Böhnisch, A., Mittermeier, M., Leduc, M. & Ludwig, R. Hot spots and climate trends of meteorological droughts in Europe–assessing the percent of normal index in a single-model initial-condition large ensemble. Front. Water 3, 716621 (2021).
Feng, H. & Zhang, M. Global land moisture trends: drier in dry and wetter in wet over land. Sci. Rep. 5, 18018 (2015).
Lian, X. et al. Multifaceted characteristics of dryland aridity changes in a warming world. Nat. Rev. Earth Environ. 2, 232–250 (2021).
Sherwood, S. & Fu, Q. A drier future? Science 343, 737–739 (2014).
Miralles, D. G. et al. El Niño–La Niña cycle and recent trends in continental evaporation. Nat. Clim. Change 4, 122–126 (2014).
Brodribb, T. J., Powers, J., Cochard, H. & Choat, B. Hanging by a thread? Forests and drought. Science 368, 261–266 (2020).
McDowell, N. G. & Allen, C. D. Darcy’s law predicts widespread forest mortality under climate warming. Nat. Clim. Change 5, 669–672 (2015).
Lobell, D. B. & Asner, G. P. Moisture effects on soil reflectance. Soil Sci. Soc. Am. J. 66, 722–727 (2002).
Tollerud, H. J., Brown, J. F. & Loveland, T. R. Investigating the effects of land use and land cover on the relationship between moisture and reflectance using landsat time series. Remote Sens. 12, 1919 (2020).
Anderegg, W. R. L., Kane, J. M. & Anderegg, L. D. L. Consequences of widespread tree mortality triggered by drought and temperature stress. Nat. Clim. Change 3, 30–36 (2013).
Greve, P., Roderick, M. L., Ukkola, A. M. & Wada, Y. The aridity index under global warming. Environ. Res. Lett. 14, 124006 (2019).
IPCC: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis (eds Masson-Delmotte, V. et al.) (Cambridge Univ. Press, 2021).
Busch, F. A. & Sage, R. F. The sensitivity of photosynthesis to O2 and CO2 concentration identifies strong Rubisco control above the thermal optimum. New Phytol. 213, 1036–1051 (2017).
Perdomo, J. A., Capó-Bauçà, S., Carmo-Silva, E. & Galmés, J. Rubisco and Rubisco activase play an important role in the biochemical limitations of photosynthesis in rice, wheat, and maize under high temperature and water deficit. Front. Plant Sci. 8, 490 (2017).
Novick, K. A. et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Change 6, 1023–1027 (2016).
Yuan, W. et al. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 5, eaax1396 (2019).
Cowan, I. R. Stomatal function in relation to leaf metablism and environment. Symp. Soc. Exp. Biol. 31, 471–505 (1977).
Humphrey, V. et al. Soil moisture–atmosphere feedback dominates land carbon uptake variability. Nature 592, 65–69 (2021).
Oren, R. et al. Survey and synthesis of intra- and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant Cell Environ. 22, 1515–1526 (1999).
Teuling, A. J. et al. A regional perspective on trends in continental evaporation. Geophys. Res. Lett. 36, L02404 (2009).
Makkink, G. F. Testing the Penman formula by means of lysimeters. J. inst. Water Eng. 11, 277–288 (1957).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Orth, R., Zscheischler, J. & Seneviratne, S. I. Record dry summer in 2015 challenges precipitation projections in Central Europe. Sci. Rep. 6, 28334 (2016).
Berg, A. et al. Land–atmosphere feedbacks amplify aridity increase over land under global warming. Nat. Clim. Change 6, 869–874 (2016).
Winkler, A. J. et al. Slowdown of the greening trend in natural vegetation with further rise in atmospheric CO2. Biogeosciences 18, 4985–5010 (2021).
Wei, Z. et al. Revisiting the contribution of transpiration to global terrestrial evapotranspiration. Geophys. Res. Lett. 44, 2792–2801 (2017).
Berg, A. & Sheffield, J. Historic and projected changes in coupling between soil moisture and evapotranspiration (ET) in CMIP5 models confounded by the role of different ET components. J. Geophys. Res. Atmos. 124, 5791–5806 (2019).
Keenan, T. F. et al. Net carbon uptake has increased through warming-induced changes in temperate forest phenology. Nat. Clim. Change 4, 598–604 (2014).
Collins, M. et al. in Climate Change 2013: The Physical Science Basis (eds Stocker, T. F. et al.) Ch. 12 (IPCC, Cambridge Univ. Press, 2013).
Nemani, R. R. et al. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 300, 1560–1563 (2003).
van der Heijden, G. M., Schnitzer, S. A., Powers, J. S. & Phillips, O. L. Liana impacts on carbon cycling, storage and sequestration in tropical forests. Biotropica 45, 682–692 (2013).
Kolby Smith, W. et al. Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization. Nat. Clim. Change 6, 306–310 (2016).
Fan, Y., Miguez-Macho, G., Jobbágy, E. G., Jackson, R. B. & Otero-Casal, C. Hydrologic regulation of plant rooting depth. Proc. Natl Acad. Sci. USA 114, 10572–10577 (2017).
Smith-Martin, C. M., Xu, X., Medvigy, D., Schnitzer, S. A. & Powers, J. S. Allometric scaling laws linking biomass and rooting depth vary across ontogeny and functional groups in tropical dry forest lianas and trees. New Phytol. 226, 714–726 (2020).
Best, M. J. et al. The plumbing of land surface models: benchmarking model performance. J. Hydrometeorol. 16, 1425–1442 (2015).
Dirmeyer, P. A. et al. Verification of land–atmosphere coupling in forecast models, reanalyses, and land surface models using flux site observations. J. Hydrometeorol. 19, 375–392 (2018).
O., S., Dutra, E. & Orth, R. Robustness of process-based versus data-driven modeling in changing climatic conditions. J. Hydrometeorol. 21, 1929–1944 (2020).
Peñuelas, J. et al. Shifting from a fertilization-dominated to a warming-dominated period. Nat. Ecol. Evol. 1, 1438–1445 (2017).
Peñuelas, J. et al. Human-induced nitrogen–phosphorus imbalances alter natural and managed ecosystems across the globe. Nat. Commun. 4, 2934 (2013).
Humphrey, V. et al. Sensitivity of atmospheric CO2 growth rate to observed changes in terrestrial water storage. Nature 560, 628–631 (2018).
Jung, M. et al. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 541, 516–520 (2017).
Martens, B. et al. GLEAM v3: satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 10, 1903–1925 (2017).
Wickham, H. et al. ggplot2: create elegant data visualisations using the grammar of graphics. R package version 3.3.5 (2022).
Bivand, R. et al. maptools: tools for handling spatial objects. R package version 1.1.2 (2022).
O’Neill, B. C. et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 9, 3461–3482 (2016).
Sen, P. K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 63, 1379–1389 (1968).
Theil, H. in Henri Theil’s Contributions to Economics and Econometrics: Econometric Theory and Methodology (eds Raj, B. & Koerts, J.) 345–381 (Springer, 1992); https://doi.org/10.1007/978-94-011-2546-8_20
Barton, K. MuMIn: multi-model inference. R package version 1.40.4 (2018).
Burnham, K. P. & Anderson, D. R. Multimodel inference: understanding AIC and BIC in model selection. Sociol. Methods Res. 33, 261–304 (2004).
Fernández-Martínez, M. et al. The role of climate, foliar stoichiometry and plant diversity on ecosystem carbon balance. Glob. Change Biol. 26, 7067–7078 (2020).
Groemping, U. Relative importance for linear regression in R: the package relaimpo. J. Stat. Softw. 17, 1–27 (2007).
Acknowledgements
J.M.C.D., W.L. and R.O. are supported through funding from the German Research Foundation (Emmy Noether grant no. 391059971). A.J.P. acknowledges support from the Australian Research Council (grant no. CE170100023). We thank the climate modelling groups for simulations to the CMIP6 selection and making their model output available.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
R.O., A.J.T. and J.M.C.D. jointly designed the study. S.K. wrote the code for downloading the CMIP6 model simulations from the Google cloud CMIP6 storage. J.M.C.D. performed the analyses and drafted the article. A.J.P, A.J.T., A.J.W., C.Z., J.M.C.D., M.M., M.R., R.O., S.K. and W.L. contributed to the writing of the paper, the discussion and interpretation of the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Climate Change thanks Paul Dirmeyer and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–20, Discussion and Tables 1–4.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Denissen, J.M.C., Teuling, A.J., Pitman, A.J. et al. Widespread shift from ecosystem energy to water limitation with climate change. Nat. Clim. Chang. 12, 677–684 (2022). https://doi.org/10.1038/s41558-022-01403-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41558-022-01403-8
This article is cited by
-
Ultra-high freshwater production in multistage solar membrane distillation via waste heat injection to condenser
Nature Communications (2024)
-
Global critical soil moisture thresholds of plant water stress
Nature Communications (2024)
-
Disentangling contributions to past and future trends in US surface soil moisture
Nature Water (2024)
-
Past and future adverse response of terrestrial water storages to increased vegetation growth in drylands
npj Climate and Atmospheric Science (2023)
-
Evidence and attribution of the enhanced land carbon sink
Nature Reviews Earth & Environment (2023)