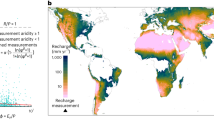
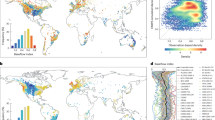
Abstract
Groundwater, the largest available store of global freshwater1, is relied upon by more than two billion people2. It is therefore important to quantify the spatiotemporal interactions between groundwater and climate. However, current understanding of the global-scale sensitivity of groundwater systems to climate change3,4—as well as the resulting variation in feedbacks from groundwater to the climate system5,6—is limited. Here, using groundwater model results in combination with hydrologic data sets, we examine the dynamic timescales of groundwater system responses to climate change. We show that nearly half of global groundwater fluxes could equilibrate with recharge variations due to climate change on human (~100 year) timescales, and that areas where water tables are most sensitive to changes in recharge are also those that have the longest groundwater response times. In particular, groundwater fluxes in arid regions are shown to be less responsive to climate variability than in humid regions. Adaptation strategies must therefore account for the hydraulic memory of groundwater systems, which can buffer climate change impacts on water resources in many regions, but may also lead to a long, but initially hidden, legacy of anthropogenic and climatic impacts on river flows and groundwater-dependent ecosystems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Digital data sets of the main geomatic results for the water table ratio and groundwater response times maps are freely available for download as geotiffs from https://doi.org/10.6084/m9.figshare.7393304.
References
Taylor, R. G. et al. Ground water and climate change. Nat. Clim. Change 3, 322–329 (2013).
Jasechko, S. et al. Global aquifers dominated by fossil groundwaters but wells vulnerable to modern contamination. Nat. Geosci. 10, 425–429 (2017).
Döll, P. Vulnerability to the impact of climate change on renewable groundwater resources: a global-scale assessment. Environ. Res. Lett. 4, 035006 (2009).
Green, T. R. et al. Beneath the surface of global change: impacts of climate change on groundwater. J. Hydrol. 405, 532–560 (2011).
Maxwell, R. M. & Kollet, S. J. Interdependence of groundwater dynamics and land-energy feedbacks under climate change. Nat. Geosci. 1, 665–669 (2008).
Maxwell, R. M. & Condon, L. E. Connections between groundwater flow and transpiration partitioning. Science 353, 377–380 (2016).
Cole, J. J. et al. Plumbing the global carbon cycle: integrating inland waters into the terrestrial carbon budget. Ecosystems 10, 172–185 (2007).
Cuthbert, M. O. et al. Modelling the role of groundwater hydro-refugia in East African hominin evolution and dispersal. Nat. Commun. 8, 15696 (2017).
Fan, Y., Li, H. & Miguez-Macho, G. Global patterns of groundwater table depth. Science 339, 940–943 (2013).
Xu, X. & Liu, W. The global distribution of Earth’s critical zone and its controlling factors. Geophys. Res. Lett. 44, 3201–3208 (2017).
Gleeson, T., Marklund, L., Smith, L. & Manning, A. H. Classifying the water table at regional to continental scales. Geophys. Res. Lett. 38, L05401 (2011).
Haitjema, H. M. & Mitchell‐Bruker, S. Are water tables a subdued replica of the topography? Groundwater 43, 781–786 (2005).
Koirala, S. et al. Global distribution of groundwater–vegetation spatial covariation. Geophys. Res. Lett. 44, 4134–4142 (2017).
Schenk, H. J. & Jackson, R. B. Mapping the global distribution of deep roots in relation to climate and soil characteristics. Geoderma 126, 129–140 (2005).
Carr, E. & Simpson, M. Accurate and efficient calculation of response times for groundwater flow. J. Hydrol. 558, 470–481 (2017).
Döll, P., Kaspar, F. & Lehner, B. A global hydrological model for deriving water availability indicators: model tuning and validation. J. Hydrol. 270, 105–134 (2003).
Döll, P., Douville, H., Güntner, A., Schmied, H. M. & Wada, Y. Modelling freshwater resources at the global scale: challenges and prospects. Surv. Geophys. 37, 195–221 (2016).
Sood, A. & Smakhtin, V. Global hydrological models: a review. Hydrol. Sci. J. 60, 549–565 (2015).
Wood, E. F. et al. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 47, W05301 (2011).
Koirala, S., Yeh, P. J. F., Hirabayashi, Y., Kanae, S. & Oki, T. Global‐scale land surface hydrologic modeling with the representation of water table dynamics. J. Geophys. Res. Atmos. 119, 75–89 (2014).
Milly, P. C. et al. An enhanced model of land water and energy for global hydrologic and earth-system studies. J. Hydrometeorol. 15, 1739–1761 (2014).
Schaller, M. F. & Fan, Y. River basins as groundwater exporters and importers: Implications for water cycle and climate modeling. J. Geophys. Res. Atmos. 114, D04103 (2009).
Ajami, H., McCabe, M. F., Evans, J. P. & Stisen, S. Assessing the impact of model spin‐up on surface water–groundwater interactions using an integrated hydrologic model. Water Resour. Res. 50, 2636–2656 (2014).
Schulz, S. et al. Improving large-scale groundwater models by considering fossil gradients. Adv. Water Resour. 103, 32–43 (2017).
Befus, K. M., Jasechko, S., Luijendijk, E., Gleeson, T. & Cardenas, M. B. The rapid yet uneven turnover of Earth’s groundwater. Geophys. Res. Lett. 44, 5511–5520 (2017).
Van Lanen, H. A. J. et al. Hydrological drought across the world: impact of climate and physical catchment structure. Hydrol. Earth Syst. Sci. 17, 1715–1732 (2013).
Bloomfield, J. P. & Marchant, B. P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci. 17, 4769–4787 (2013).
Damkjaer, S. & Taylor, R. The measurement of water scarcity: defining a meaningful indicator. Ambio 46, 513–531 (2017).
Alley, W. M. et al. Flow and storage in groundwater systems. Science 296, 1985–1990 (2002).
Döll, P. & Fiedler, K. Global-scale modeling of groundwater recharge. Hydro. Earth Syst. Sci. 12, 863–885 (2008).
Domenico, P. A. & Schwartz, F. W. Physical and Chemical Hydrogeology Vol. 506 (Wiley, New York, NY, 1998).
Downing, R., Oakes, D., Wilkinson, W. & Wright, C. Regional development of groundwater resources in combination with surface water. J. Hydrol. 22, 155–177 (1974).
Erskine, A. & Papaioannou, A. The use of aquifer response rate in the assessment of groundwater resources. J. Hydrol. 202, 373–391 (1997).
Currell, M., Gleeson, T. & Dahlhaus, P. A new assessment framework for transience in hydrogeological systems. Groundwater 54, 4–14 (2014).
Townley, L. R. The response of aquifers to periodic forcing. Adv. Water Resour. 18, 125–146 (1995).
Lehner, B., Verdin, K. & Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos 89, 93–94 (2008).
Lehner, B. & Grill, G. Global river hydrography and network routing: baseline data and new approaches to study the world’s large river systems. Hydrol. Process. 27, 2171–2186 (2013).
Alcamo, J. et al. Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol. Sci. J. 48, 317–337 (2003).
Atlas of the World. 9th edn (National Geographic Society, Washington, DC, 2010).
Gleeson, T., Moosdorf, N., Hartmann, J. & Beek, L. A glimpse beneath earth’s surface: GLobal HYdrogeology MaPS (GLHYMPS) of permeability and porosity. Geophys. Res. Lett. 41, 3891–3898 (2014).
Condon, L. E. & Maxwell, R. M. Evaluating the relationship between topography and groundwater using outputs from a continental-scale intergrated hydrology model. Water Resour. Res. 51, 6602–6621 (2015).
Danielson, J. J. & Gesch, D. B. Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010) Report no. 2331–1258 (US Geological Survey, 2011).
Rushton, K. R. & Redshaw, S. C. Seepage and Groundwater Flow: Numerical Analysis by Analog and Digital Methods (Wiley, New York, NY, 1979).
De Graaf, I. E. M. et al. A global-scale two-layer transient groundwater model: development and application to groundwater depletion. Adv. Water Resour. 102, 53–67 (2017).
Rousseau‐Gueutin, P. et al. Time to reach near‐steady state in large aquifers. Water Resour. Res. 49, 6893–6908 (2013).
Cuthbert, M. O. Straight thinking about groundwater recession. Water Resour. Res. 50, 2407–2424 (2014).
Cuthbert, M. O. et al. Understanding and quantifying focused, indirect groundwater recharge from ephemeral streams using water table fluctuations. Water Resour. Res. 52, 827–840 (2016).
Walker, G. R., Gilfedder, M., Dawes, W. R. & Rassam, D. W. Predicting aquifer response time for application in catchment modeling. Groundwater 53, 475–484 (2015).
Seybold, H., Rothman, D. H. & Kirchner, J. W. Climate’s watermark in the geometry of stream networks. Geophys. Res. Lett. 44, 2272–2280 (2017).
Gleeson, T. & Manning, A. H. Regional groundwater flow in mountainous terrain: three‐dimensional simulations of topographic and hydrogeologic controls. Water Resour. Res. 44, W10403 (2008).
Gleeson, T. et al. Mapping permeability over the surface of the Earth. Geophys. Res. Lett. 38, L02401 (2011).
De Graaf, I. E. M. et al. A high-resolution global-scale groundwater model. Hydrol. Earth Syst. Sci. 19, 823–837 (2015).
Wada, Y. et al. Global depletion of groundwater resources. Geophys. Res. Lett. 37, L20402 (2010).
Bruggeman, G. A. (ed.) Analytical Solutions of Geohydrological Problems Vol. 46 (Developments in Water Science, Elsevier, Amsterdam, 1999).
Acknowledgements
The authors acknowledge funding for an Independent Research Fellowship from the UK Natural Environment Research Council (NE/P017819/1) (to M.O.C.); the German Science Foundation DFG (Cluster of Excellence ‘CliSAP’, EXC177, Universität Hamburg) and Bundesministerium für Bildung und Forschung Project PALMOD (ref. 01LP1506C) (to J.H.); the German Federal Ministry of Education and Research (BMBF) (grant no. 01LN1307A) (to N.M.); the Agence Nationale de la Recherche (ANR grant ANR-14-CE01-00181-01) and the French national programme LEFE/INSU (to A.S.); and the Natural Sciences and Engineering Research Council of Canada (NSERC) (Discovery grant RGPIN/341992) (to B.L.).
Author information
Authors and Affiliations
Contributions
The idea for the paper was conceived by M.O.C. and T.G. Analyses were carried out by all authors. The manuscript was written by M.O.C. with input from all authors.
Corresponding author
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–13, Supplementary References.
Rights and permissions
About this article
Cite this article
Cuthbert, M.O., Gleeson, T., Moosdorf, N. et al. Global patterns and dynamics of climate–groundwater interactions. Nature Clim Change 9, 137–141 (2019). https://doi.org/10.1038/s41558-018-0386-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41558-018-0386-4
This article is cited by
-
A millennium-long perspective on recent groundwater changes in the Iberian Peninsula
Communications Earth & Environment (2024)
-
Development of Groundwater Levels Dataset for Chile since 1970
Scientific Data (2024)
-
Groundwater decline is global but not universal
Nature (2024)
-
Ending groundwater overdraft without affecting food security
Nature Sustainability (2024)
-
Millennium-scale changes in the Atlantic Multidecadal Oscillation influenced groundwater recharge rates in Italy
Communications Earth & Environment (2024)