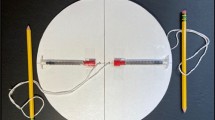
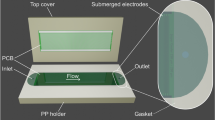
Abstract
In a global-health context, commercial centrifuges are expensive, bulky and electricity-powered, and thus constitute a critical bottleneck in the development of decentralized, battery-free point-of-care diagnostic devices. Here, we report an ultralow-cost (20 cents), lightweight (2 g), human-powered paper centrifuge (which we name ‘paperfuge’) designed on the basis of a theoretical model inspired by the fundamental mechanics of an ancient whirligig (or buzzer toy; 3,300 bc). The paperfuge achieves speeds of 125,000 r.p.m. (and equivalent centrifugal forces of 30,000 g), with theoretical limits predicting 1,000,000 r.p.m. We demonstrate that the paperfuge can separate pure plasma from whole blood in less than 1.5 min, and isolate malaria parasites in 15 min. We also show that paperfuge-like centrifugal microfluidic devices can be made of polydimethylsiloxane, plastic and 3D-printed polymeric materials. Ultracheap, power-free centrifuges should open up opportunities for point-of-care diagnostics in resource-poor settings and for applications in science education and field ecology.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$99.00 per year
only $8.25 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Mabey, D., Peeling, R. W., Ustianowski, A. & Perkins, M. D. Tropical infectious diseases: diagnostics for the developing world. Nat. Rev. Microbiol. 2, 231–240 (2004).
Al-Soud, W. A. & Rådström, P. Purification and characterization of PCR-inhibitory components in blood cells. J. Clin. Microbiol. 39, 485–493 (2001).
Singleton, J. et al. Electricity-free amplification and detection for molecular point-of-care diagnosis of HIV-1. PLoS ONE 9, e113693 (2014).
LaBarre, P., Boyle, D., Hawkins, K. & Weigl, B. Instrument-free nucleic acid amplification assays for global health settings. Proc. SPIE 8029, 802902 (2011).
Niemz, A., Ferguson, T. M. & Boyle, D. S. Point-of-care nucleic acid testing for infectious diseases. Trends Biotechnol. 29, 240–250 (2011).
Brown, J. et al. A hand-powered, portable, low-cost centrifuge for diagnosing anemia in low-resource settings. Am. J. Trop. Med. Hyg. 85, 327–332 (2011).
Wong, A. P., Gupta, M., Shevkoplyas, S. S. & Whitesides, G. M. Egg beater as centrifuge: isolating human blood plasma from whole blood in resource-poor settings. Lab Chip 8, 2032–2037 (2008).
Mariella, R. Jr Sample preparation: the weak link in microfluidics-based biodetection. Biomed. Microdevices 10, 777–784 (2008).
Dineva, M. A., Mahilum-Tapay, L. & Lee, H. Sample preparation: a challenge in the development of point-of-care nucleic acid-based assays for resource-limited settings. Analyst 132, 1193–1199 (2007).
Urdea, M. et al. Requirements for high impact diagnostics in the developing world. Nature 444, 73–79 (2006).
Bohr, J. & Olsen, K. The ancient art of laying rope. Europhys. Lett. 93, 60004 (2011).
van der Heijden, G. H. M. & Thompson, J. M. T. Helical and localised buckling in twisted rods: a unified analysis of the symmetric case. Nonlinear Dynam. 21, 71 (2000).
Ricca, R. L. The energy spectrum of a twisted flexible string under elastic relaxation. J. Phys. A: Math. Gen. 28, 2335–2352 (1995).
Freund, H. J. Time control of hand movements. Prog. Brain Res. 64, 287–294 (1986).
Schlichting, H. J. & Suhr, W. The buzzer—a novel physical perspective on a classical toy. Eur. J. Phys. 31, 501–510 (2010).
Adeoye, G. O. & Nga, I. C. Comparison of quantitative buffy coat technique (QBC) with giemsa-stained thick film (GTF) for diagnosis of malaria. Parasitol. Int. 56, 308–312 (2007).
Gorkin, R. et al. Centrifugal microfluidics for biomedical applications. Lab Chip 10, 1758–1773 (2010).
Cybulski, J. S., Clements, J. & Prakash, M. Foldscope: origami-based paper microscope. PLoS ONE 9, e98781 (2014).
Martinez, A. W., Phillips, S. T., Whitesides, G. M. & Carrilho, E. Diagnostics for the developing world: microfluidic paper-based analytical devices. Anal. Chem. 82, 3–10 (2010).
Yager, P. et al. Microfluidic diagnostic technologies for global public health. Nature 442, 412–418 (2006).
Xu, S. & Nadim, A. Oscillatory counter-centrifugation. Phys. Fluids 28, 021302 (2016).
Acknowledgements
We thank all members of the PrakashLab for their feedback. We thank J. Cybulski and D. Ott for their discussions and engagement in the early phases of this project; F. Hol for his assistance with the soft-lithography fabrication; and K. Hong (Yeh Lab, Stanford University) for her assistance with the malaria samples. M.S.B. acknowledges fellowship support from the Stanford School of Medicine Dean’s Postdoctoral Fellowship. M.P. acknowledges support from the Pew Foundation, Moore Foundation, National Science Foundation Career Award and the National Institutes of Health (NIH) New Innovator Award. This work was supported by the Stanford Clinical and Translational Science Award (CTSA) to Spectrum (UL1 TR001085). The CTSA programme is led by the National Center for Advancing Translational Sciences (NCATS) at the NIH. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Author information
Authors and Affiliations
Contributions
M.S.B. and M.P. designed the research; M.S.B., B.B., C.C., G.K. and A.J. performed and analysed the research; all authors wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary discussion, figures and video captions. (PDF 4234 kb)
Video 1
High-speed dynamics of paperfuge. (MP4 14217 kb)
Video 2
Measuring rotational speed. (MP4 18475 kb)
Video 3
Twisting torque conditions. (MP4 10556 kb)
Video 4
Comparison of experiment and theory. (MP4 8818 kb)
Video 5
Separation of plasma from whole blood using paperfuge. (MP4 43381 kb)
Rights and permissions
About this article
Cite this article
Bhamla, M., Benson, B., Chai, C. et al. Hand-powered ultralow-cost paper centrifuge. Nat Biomed Eng 1, 0009 (2017). https://doi.org/10.1038/s41551-016-0009
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41551-016-0009
This article is cited by
-
An ultralow-cost portable centrifuge from discarded materials for medical applications
Scientific Reports (2023)
-
Beyond assembly: the increasing flexibility of single-molecule sequencing technology
Nature Reviews Genetics (2023)
-
Smartphone-based platforms implementing microfluidic detection with image-based artificial intelligence
Nature Communications (2023)
-
Whirligig-Inspired Hybrid Nanogenerator for Multi-strategy Energy Harvesting
Advanced Fiber Materials (2023)
-
Materials, assemblies and reaction systems under rotation
Nature Reviews Materials (2022)