Main

The outer atmospheres of solar-like stars are known to be heated to temperatures in excess of a million degrees, emitting radiation at X-ray and extreme-ultraviolet wavelengths1,2,3. These stars are also thought to shed a hot, magnetized wind, leading to sustained mass loss4. Both of these factors can influence the evolution and habitability of planetary systems5,6. The winds also enable angular momentum loss by providing a torque that has a pivotal role in a star’s evolution7,8. However, the physical processes that convert magnetic energy to power the stellar atmospheric dynamics are still poorly understood.

A promising candidate is the dissipation of Alfvénic waves, which has received support from numerical models of wave propagation through stellar atmospheres, typically based on phenomological turbulence9,10,11,12,13 and/or shock heating14,15,16. These models rely on turbulence (for example, incompressible magnetohydrodynamic turbulence; turbulence due to instabilities) as a means to cascade wave energy from the driving to dissipation scales17. Such turbulence-driven models have shown promise for predicting large-scale plasma parameters in the solar wind18,19, simulating the environment around planet-hosting stars20 and studying the long-term evolution of solar-like stars21. Although such results are encouraging, the models typically contain several critical, but unconstrained, parameters that ultimately control the details of the energy transport and deposition by the waves.

One such parameter is the perpendicular correlation length (L⊥), which represents an effective transverse length of the turbulence for the largest ‘outer scale’ eddies. This parameter has been shown phenomenologically to be related to the turbulent heating rate22, and also controls how (that is, the rate of turbulent to shock heating) and where the energy is deposited in the coronal plasma10,16. Because of this, the value of the correlation length strongly influences the wind speed10,16. Larger values lead to greater wave damping occurring above the critical point, where wave energy is converted almost entirely to kinetic energy23. In turn, the wind speed has a role in determining the torque from the winds and could influence magnetic breaking21. On these aspects, the magnitude of the effect of varying the correlation length is comparable to variations in the rotation period of the star21. The value of the correlation length also weakly influences the maximum coronal temperature, mass-loss rate and location of the Alfvén critical zone in coronal holes10. However, other parameters have a larger influence on these latter aspects, such as the Alfvén wave flux into the corona10,16,24, the global magnetic structure25,26 and the rotation period of the star21,27.

Previous efforts to measure the perpendicular correlation length have only been able to obtain values in the outer corona (that is, >10 R⊙) and heliosphere, far from the coronal base where the Alfvénic waves are injected28,29,30,31,32,33,34,35. However, the Alfvénic waves have potentially undergone substantial evolution through the low and middle corona due to fine-scale plasma inhomogeneities36,37. Hence, it is potentially non-trivial to map the values for correlation length back to the Sun. Here we estimate present measurements for the perpendicular correlation length at the coronal base (from 1.05 R⊙), an order of magnitude closer to the Sun than previous estimates.

We use observations from the Coronal Multi-channel Polarimeter (CoMP)38 instrument, and its recently upgraded version (UCoMP)39, to measure the perpendicular correlation length in the inner corona. CoMP and UCoMP can observe the off-limb solar corona between 1.05 R⊙ and 1.35 R⊙ (about 1.95 R⊙ for UCoMP) in near-infrared passbands (further details on data used are given in Methods). To create imaging time-series, we estimated the intensity (Fig. 1a) and line-of-sight (LOS) Doppler velocity (Fig. 1b) by using a single Gaussian model to fit the spectral profiles of the Fe xiii (1,074.7 nm) emission line. The series of images enabled the identification of the ubiquitous propagating Alfvénic fluctuations in the fine-scale magnetized structures throughout the corona, whose presence in the solar atmosphere is now well established40,41,42.

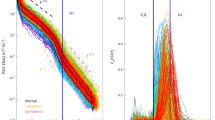
Fig. 1: Alfvénic waves and perpendicular correlation length (L⊥) estimation.
figure 1

a, CoMP Fe xiii (1,074.7 nm) intensity image taken at 19:04:35 UT on 20 April 2015. b, LOS Doppler velocity map from the Fe xiii (1,074.7 nm) emission line. The location of an artificial slit (S) across coronal loops at the base of the pseudostreamer is marked with a solid line. c, LOS Doppler velocity time–distance diagram from the artificial slit. The image shows the wave fronts of transverse Alfvénic motions as they propagate along the loop structure. The wave fronts can be seen to be coherent up scales of ~10 Mm. d, Example of the perpendicular correlation length estimation from local coherence maps. Neighbourhoods centred on a reference pixel are extracted from the Doppler velocity data (for example, box in b). The panel shows a map of the measure of coherence of Doppler velocity signals within the local neighbourhood with respect to the reference pixel. The reference pixel is located at the centre (0, 0) of the region (and indicated by the cross in b). The dark island in the middle is the high-coherence region that is modelled with a two-dimensional Gaussian, centred on the reference pixel. The black ellipse is derived from the fitted model and shows the region where the coherence is greater than exp(−0.5), with the orthogonal standard deviations also indicated (σ⊥,∥).

Full size image

An example of the perpendicular spatial scales associated with the waves is obtained by extracting a line of pixels across the large bundle of quiescent coronal loops (shown in Fig. 1b). This artificial slit is orientated perpendicular to the local magnetic field. The loops are visible in the lower part of Fig. 1a (and also strikingly visible in Doppler velocity; Fig. 1b) and are associated with a pseudostreamer (Fig. 2). The Doppler velocities, as shown in Fig. 1b, contain the signature of the large-scale rotation of the corona. To reveal the scales of the fluctuations, we subtract the temporal mean at each spatial location and apply a frequency filter centred on 3.5 mHz (Methods), coinciding with a frequency range showing enhanced wave power42. The resulting filtered velocity time–distance diagram is shown in Fig. 1c and it reveals the wave fronts associated with the propagating Alfvénic waves. It is evident from the time–distance diagram that the waves possess spatial coherence on scales up to tens of megametres. This is in contrast to the spatial scales associated with the fine-scale structure of the coronal loops, that is, ≤1 Mm (refs. 43,44). This suggests that, locally, multiple individual coronal structures are oscillating coherently.

Fig. 2: Estimates for the perpendicular coherence length scales.
figure 2

The graph in the middle shows the probability density plots for the perpendicular coherence length (σ⊥) obtained from multiple CoMP and UCoMP datasets. The inner annular region of the figure shows an example of a global perpendicular coherence length map for the data taken on 20 April 2015. Due to low signal to noise, L⊥ could not be estimated for certain pixels near the poles. The colour bar for the map is shown at the bottom. The map shows the spatial features of the coherence length, which is relatively homogeneous throughout the inner corona. The outer region of the panel is an image of the inner corona and beginning of the middle corona as viewed in white light with K-Cor. It gives an impression of how the different magnetic structures found in the inner corona connect to the outer heliosphere. A few notable features have been indicated.

Full size image

To characterize the transverse length scales associated with the waves, we estimate the mean-squared coherence (MSC) between the frequency-filtered (~3.5 mHz) LOS Doppler velocity time-series at each pixel and its local neighbours (Fig. 1d). A thorough description is given in Methods but we provide a brief outline here. The MSC magnitudes are estimated by using the Fourier cross-spectra of the time series in a local region with a reference pixel, and provide a local spatial distribution for the MSC values. As Alfvénic fluctuations propagate along the magnetic field, the coherence distribution for these waves is also elongated along the magnetic field (compared with the perpendicular direction; Fig. 1d). These elongated islands of high coherence (MSC > 0.5) are then modelled using a two-dimensional Gaussian function (Methods) to obtain the measure of orthogonal length scales in terms of the standard deviation (σ⊥,∥). The perpendicular component of the estimated standard deviations (σ⊥) represents the length scales perpendicular to the direction of propagation for the Alfvénic fluctuations.

The global map of the perpendicular coherence (σ⊥) in the solar atmosphere for a sample dataset is shown in Fig. 2. The estimated magnitudes for the perpendicular coherence suggest length scales in the range 2–20 Mm. The probability density distributions of the estimated coherence for multiple datasets indicate that the peak values are centred around 5–6.5 Mm. The peak magnitudes of the coherence distribution correspond to the perpendicular correlation length scales of L⊥ ≈ 7.6–9.3 Mm (1/e folding) in the inner corona. These results for coronal turbulent injection scales are comparable to the average supergranular cell diameter in the solar photosphere45,46. Hence they are consistent with the expected expansion of intense kilogauss magnetic fields from the photosphere to corona. Similar values of perpendicular correlation length have been used in Alfvénic turbulence models based on phenomenological considerations9,12. These values are consistent across the nine-year span of the different datasets, suggesting little variation across the solar cycle. Although, we note that there is a five-year period during the solar minimum when no observations are present.

The global map of coherence also shows that the values are relatively homogeneous throughout the quiescent corona. There are numerous magnetic structures within the CoMP field of view, which connect to the middle corona (1.5–6 R⊙) in different ways. This connection is partly visible in the white-light image from the K-Coronagraph instrument (K-Cor) shown in Fig. 2 (see Methods for details on K-Cor). An extended image revealing the connection of the inner coronal structures to the outer corona and heliosphere is given in Supplementary Fig. 1. Examination of the coherence values between closed (for example, those at the base of pseudostreamers) and open (for example, equatorial coronal holes) magnetic-field topologies suggests there is no difference in distributions of the values. This implies that the Alfvénic fluctuations found regularly in the fast solar wind, and more recently in some components of the slow wind47, will contain the same perpendicular scales.

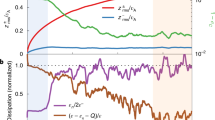
The values of L⊥ measured here with (U)CoMP are the closest measurements to the Sun of the transverse-wave scales associated with Alfvénic fluctuations. The waves observed here, at the coronal base, are the ones that will propagate outwards into the wind along open magnetic-field lines. Hence they should provide a stringent constraint for wave-based models of Alfvénically driven solar and stellar winds. In Fig. 3, we compare the measurements at the base of solar corona with previous measurements (radio and in situ) in the outer corona and interplanetary medium (we provide a summary of the previous observations in Supplementary Information). These values are further scrutinized with two models that provide theoretical estimates for the radial evolution of perpendicular correlation length parameter (L⊥) from the photosphere to near-Earth space environment at 1 au (reproduced from ref. 48). The first model (M1) describes the evolution of L⊥ assuming that the length scale varies in proportion to the expansion of the magnetic fields with radial distance49. Meanwhile, the second model (M2) incorporates a description of the coupling between the background plasma flows and the Alfvénic fluctuations for fast solar wind conditions48. There is clear tension between the values measured here from the CoMP data (shown by diamond in Fig. 3) and those farther from the Sun. The models for the evolution of L⊥ that capture the estimated correlation lengths from the in situ measurements beyond the Alfvén critical zone indicate the value of L⊥ in the inner corona to be ~1 Mm. This is nearly an order of magnitude smaller than the L⊥ we report here. To describe the in situ results, the models are initiated in the photosphere with a perpendicular correlation length of 0.12 Mm. This length scale would imply that the Alfvénic waves are excited at the photosphere by turbulent motions within individual magnetic flux tubes, which have diameters of ~0.1−0.3 Mm (refs. 50,51). A re-scaling of the M1 model to pass through the results obtained here, in the inner corona, would imply a photospheric correlation length of ~1.5 Mm, comparable to the scale of granulation. However, at 1 au, the re-scaled model overestimates the correlation length compared with the measured values from in situ data.

Fig. 3: Comparison of estimated scales at the base of solar corona with previous measurements.
figure 3

A comparison between the perpendicular correlation length scales (L⊥) at the base of the solar corona (diamonds) with previous estimates in the inner heliosphere (plus symbols) and near-Earth at 1 au (cross symbols). Estimates for the inner heliosphere and at 1 au are from refs. 28,29,30,31,32,33,34,35. The evolution of these transverse energy injection scales in the heliosphere is compared with two numerical models that correspond to theoretical assumptions regarding magnetic-field expansion (M1) and coupling between flows and waves (M2). The models were previously calculated in ref. 48 for an initial photospheric correlation length of 120 km. The shaded region highlights the Alfvén critical zone between 10 R⊙ and 20 R⊙ in the inner heliosphere.

Full size image

A possible explanation for this contradiction arises from the underlying physical assumptions present in the majority of global Alfvén wave turbulence models of the corona and solar wind (and hence L⊥ evolution in M1 and M2 models), which do not reflect the actual conditions in the solar atmosphere. The global models typically assume that the plasma comprising the corona and (fast) solar wind, which emanates from coronal holes and/or polar regions, is homogeneous in the direction perpendicular to the magnetic field10,11,12,13,16,25,48,52. Under the assumption of a homogeneous plasma, the Alfvén waves are able to oscillate on individual magnetic-field lines or surfaces without interaction.

However, recent observations of the inner53 and outer36 corona suggest that the coronal plasma is inhomogeneous in the direction perpendicular to the magnetic field (this has been widely acknowledged to be the case for active regions since at least the 1990s; for example, ref. 54). The fine density structuring is observed out to at least 14 R⊙ (ref. 36). The presence of inhomogeneity perpendicular to the magnetic field in a plasma implies the Alfvénic waves must be surface Alfvén modes55. This means that resonances can occur within the inhomogeneous regions that strongly influence the characteristics of the propagating Alfvénic waves37,56. The resonances are able to concentrate Alfvénic wave energy to smaller spatial scales through an Alfvénic-to-Alfvénic mode conversion, typically on the length scales of the inhomogeneity37,57. Hence, including the wave physics arising from a highly structured plasma in the global wind models could lead to a shortening of the perpendicular length scales as the waves propagate, acting in tension to the magnetic-field expansion and curbing the growth of the perpendicular correlation length with radial distance. While circumstantial, the spatial scales of the inhomogeneity at 14 R⊙ are present down to ~20 Mm (ref. 36) in line with the radio measurements of the L⊥ from ref. 31. In Supplementary Information, we provide a more speculative discussion on the role of the Alfvén critical zone in modifying the perpendicular correlation length.

Another point to consider is that the degree of correlation calculated here is for Alfvénic waves with frequencies close to 3.5 mHz. Previous work40,42 has demonstrated the presence on enhanced Alfvénic wave power around these frequencies, which has been linked to the mode conversion of acoustic modes58,59. Hence the measured correlation length scales could be indicative of wave driving by acoustic mode conversion, with another (or many other) perpendicular length scale(s) associated with different wave drivers (for example, granular flows, internal motions of magnetic flux tubes). At present, Alfvén wave turbulence models generally do not consider the influence of two or more populations of Alfvénic waves, although recent modelling including Alfvénic waves generated through mode conversion of longitudinal waves and photospheric driving (but with the same value of L⊥) suggests the additional Poynting flux can increase mass-loss rates60.

In summary, here we have provided estimates for the perpendicular correlation lengths of Alfvénic waves in the solar corona at heights of 1.05–1.3 R⊙, that is, the coronal base. The estimates we provide are measured considerably closer to the Sun than any previous measurements. The perpendicular correlation length is a key parameter in many global Alfvén wave models of the corona and solar wind based on phenomenological turbulence. Hence our results should provide a critical constraint on this value, which has until now been a tunable value chosen to provide agreement of model outputs with other observational constraints (for example, wind temperature, velocity). We find that the corona shows fluctuations are coherent over scales of L⊥ ≈ 7.6−9.3 Mm perpendicular to the magnetic field, which is indicative of supergranulation scales. Comparison of the results with current models of how L⊥ changes with distance from the Sun, and previous measurements, indicates that the current models of the Alfvénic waves in the solar wind are missing some physical processes below the Alfvén critical zone.

Methods

Observational data

Coronal Multi-channel Polarimeter (CoMP and UCoMP)

The multiple datasets used in our analysis were taken with the CoMP instrument and the recently upgraded instrument (UCoMP), and details are listed in Table 1. The CoMP instrument can observe the solar corona between 1.05 R⊙ and 1.3 R⊙ with a pixel size of 4.46″. UCoMP is an upgraded replacement with a larger observational range between 1.03 R⊙ and 1.95 R⊙ and pixel size of 3″. UCoMP is situated at the Mauna Loa Solar Observatory (MLSO) in Hawaii (CoMP was there from 2011 to 2018) and is fitted on a 20-cm aperture Lyot coronagraph with a Stokes polarimeter and a narrow-band electro-optically tuned birefringent filter. The details on CoMP and UCoMP instrument capabilities, data acquisition and reduction process have been described in refs. 38,39.

Table 1 Details of the datasets used in the current study
Full size table

We utilize the level 2 data available from the MLSO archive61, which have a cadence of 30 s and comprise intensity images of the corona at three wavelengths (I1 = 1,074.50 nm, I2 = 1,074.62 nm and I3 = 1,074.74 nm). These wavelengths sample the Fe xiii 1,074.7 nm emission line with a peak formation temperature of ~1.6 MK in ionization equilibrium. We note that each frame in the final data product is an average over 16 frames taken at a short exposure time. Over the period of observations listed in Table 1, there is the occasional frame of bad data due to seeing. Such frames are removed before analysis. To maintain a fixed cadence, the data gaps are replaced with a frame linearly interpolated between the temporal neighbours. The percentage of original frames in each dataset is given by the duty cycle in Table 1.

For every frame in a dataset, at each pixel, the spectral profile from three wavelength scans is modelled using a Gaussian function to estimate the central intensity (i), LOS Doppler velocity (v) and Doppler width (w) estimates. These quantities are derived using the following equations:

$$i={I}_{2}{{\mathrm{e}}}^{{v}^{2}/{w}^{2}},$$
(1)
$$w=\sqrt{\frac{-2{d}^{2}}{a+b}},$$
(2)
$$v=\frac{{w}^{2}}{4d}(a-b),$$
(3)

where d is the spectral resolution of the observations. Here, the a and b are expressed in terms of intensity at each wavelength I1, I2, I3, as

$$a=\log ({I}_{3}/{I}_{2}),\qquad b=\log ({I}_{1}/{I}_{2}).$$
(4)

Major source of uncertainties (σ) associated with Doppler velocity estimation comes from the intensity measurement at the three wavelength positions by the CoMP and UCoMP instruments. This uncertainty is a sum of contributions arising from photon (σp), background (σbg), readout (σr) and seeing (σs) noise, along with negligible contributions from dark current and flat fields. The overall uncertainty is divided by the number of exposures (m) taken for a particular image. The total uncertainty for the spectral intensity (in photon counts) is given by:

$${\sigma }_{I}^{\,2}=\frac{{\sigma }_{{\mathrm{p}}}^{\,2}+2{\sigma }_{{\mathrm{r}}}^{\,2}+{\sigma }_{{\mathrm{bg}}}^{\,2}+{\sigma }_{{\mathrm{s}}}^{\,2}}{m}.$$
(5)

Moreover, a detailed description of the uncertainties in Doppler velocity estimation are given by ref. 62. We also note that there is no absolute wavelength calibration available for CoMP and UCoMP. This means that the absolute value of Doppler shift can not be trusted. Given that we are interested in the fluctuations of the Doppler velocity, the lack of absolute wavelength scale does not impact the results.

It is worth highlighting here that the measurements of the Doppler velocity of coronal fluctuations suffer from degradation due to LOS and spatial averaging. The averaging leads to substantially reduced Doppler velocity amplitudes63,64; hence, the waves in Fig. 1 have apparently small amplitudes of ~0.6 km s−1. Comparison with transverse motions seen in the corona with the Solar Dynamics Observatory show that the actual wave amplitudes are substantially larger41,42.

K-Coronagraph

The region covering the transition from inner to middle corona is shown in Fig. 2 to provide an extended overview of coronal structures observed by CoMP and UCoMP instruments in our analysis. The K-Cor instrument is located at the MLSO and is designed to examine the K corona through measurements of polarization brightness (pB) formed by Thomson scattering of photospheric light by coronal free electrons. It observes the corona from 1.05 R⊙ to 3 R⊙ with a lower spatial sampling of ~5.6″ compared with the CoMP and UCoMP instruments but with a higher cadence of 15 s. We used the level 2 data taken on 20 April 2015 at 17:08 UT from the MLSO data archive65, which are cropped and averaged over 10 min of observation time. The data had also been subject to a radial normalizing filter66.

Time–distance diagram

The construction of the time–distance diagram in Fig. 1c is largely explained in the main text. Here we discuss the form of the frequency filter used. The filter is defined by a Gaussian function that is centred on 3.5 mHz with a standard deviation of 15 mHz. For each pixel along the artificial slit, the Doppler velocity time-series is Fourier transformed and the filter is applied in Fourier space, before taking the inverse Fourier transform.

Estimation of length scales

For two signals g(t) and h(t), the mean-squared coherence (MSC) is given by

$${\mathrm{MS{C}}}_{gh}(\,\,f\,\,)=\frac{| {F}_{gh}(\,\,f\,\,){| }^{2}}{{F}_{gg}(\,\,f\,\,){F}_{hh}(\,\,f\,\,)},$$
(6)

where Fgh(f) is the cross-spectral density between g and h, and Fgg(f) and Fhh(f) are the auto-spectral density of g and h, respectively. The MSC is a function of frequency, f. Hence, the MSC can provide a measure of the linear correlation between the LOS Doppler velocity time-series of a reference pixel with its neighbouring pixels at different frequencies.

In this work, we perform MSC calculations throughout the corona, focusing on local regions of 64 × 64 Mm centred on a reference pixel. The calculation of the correlation is performed in Fourier space, as suggested by equation (6). For each Doppler velocity time-series in the local neighbourhood, we subtract its temporal mean value, leaving only the fluctuating Doppler signal. Each time series is then subject to a Fourier transform and used to calculate the relevant cross- and auto-spectral densities. The Alfvénic waves are known to have enhanced power around 3–4 mHz (refs. 42,62). Hence, for each MSC calculation, we take a weighted sum of the the Fourier coefficients around this frequency. The weighting is defined by with a Gaussian function that is centred on 3.5 mHz with a standard deviation of 15 mHz. The MSC is calculated between the reference series and each pixel in the region (an example of such a region is shown in Fig. 1d).

The correlation length scales (L⊥) for the propagating Alfvénic waves are estimated from the spatial distribution of the MSC. The observed MSC is highly directional due to the nature of Alfvénic wave propagation (see Fig. 1d for an example), with the waves propagating only along the magnetic field. Hence the MSC is elongated along the magnetic-field direction, with a shorter degree of coherence perpendicular to the field. Hence it is possible to define two orthogonal directions with respect to Alfvénic wave propagation within the images. One component is the direction of propagation in the plane-of-sky (which we call the parallel direction). The other component is perpendicular to the plane-of-sky propagation direction, which is perpendicular to the magnetic-field orientation.

Next, we select only those pixels within the local region that have an MSC greater than 0.5 for use in the estimation of the length scales. As the Alfvénic waves propagate along the magnetic fields, the MSC distribution tends to appear like elongated elliptical regions or ‘islands’ (Fig. 1d), which we model using a two-dimensional Gaussian function as given below:

$$G(x,y,{\sigma }_{\perp },{\sigma }_{\parallel },\theta )=A{{\mathrm{e}}}^{\left(-(a{(x-{\mu }_{x})}^{2}+2b(x-{\mu }_{x})(y-{\mu }_{y})+c{(y-{\mu }_{y})}^{2})\right)},$$
(7)

where

$$a=\frac{{\cos }^{2}\theta }{2{\sigma }_{\perp }^{2}}+\frac{{\sin }^{2}\theta }{2{\sigma }_{\parallel }^{2}},$$
(8)
$$b=-\frac{\sin 2\theta }{4{\sigma }_{\perp }^{2}}+\frac{\sin 2\theta }{4{\sigma }_{\parallel }^{2}},$$
(9)
$$c=\frac{{\sin }^{2}\theta }{2{\sigma }_{\perp }^{2}}+\frac{{\cos }^{2}\theta }{2{\sigma }_{\parallel }^{2}}.$$
(10)

Here σ⊥,∥ are the standard deviation in the orthogonal directions, μx,y are the mean values in the horizontal and vertical directions, A is the amplitude and θ is the angle of rotation with respect to the vertical. The σ⊥ provides the estimates for the perpendicular coherence (hence, correlation length scales, L⊥) associated with the propagating Alfvénic waves in the coronal environment.

As the function is fit to the central pixel in a local neighbourhood, the mean values, μx,y, are both fixed to zero. Further, the amplitude of the MSC has a maximum of 1, which occurs at (0, 0), hence is fixed to 1. Equation (7) then reduces to:

$$G(x,y,{\sigma }_{\perp },{\sigma }_{\parallel },\theta )={{\mathrm{e}}}^{\left(-(a{x}^{2}+2bxy+c{y}^{2})\right)},$$
(11)

with a, b and c unchanged. This means that only three parameters are required to be estimated for G, that is, σ⊥,∥ and θ. The function is fit using an L2 regularized maximum likelihood approach, where the uncertainties on the MSC values are assumed to be normally distributed. In addition, we also include a free parameter for the noise in the MSC, ψ, through the inclusion of extra terms in the likelihood, and this parameter is determined for each individual MSC island. The log-likelihood function used is given by

$$\log {{{\mathcal{L}}}}=-\frac{N}{2}\log (2\uppi {\psi }^{2})-\frac{1}{2{\psi }^{2}}\mathop{\sum }\limits_{i=1}^{N}{({\mathrm{MS{C}}}_{i}-{G}_{i})}^{2}-\frac{{\sigma }_{\perp }^{\,2}}{2{\lambda }_{{\mathrm{reg}}}^{2}}-\frac{{\sigma }_{\parallel }^{\,2}}{2{\lambda }_{{\mathrm{reg}}}^{2}},$$
(12)

where N is the number of pixels with MSC > 0.5, MSCi is the observed MSC value at location i and Gi is Gaussian model prediction for the MSC value. The L2 regularization is provide by the final two terms in the likelihood. The regularization penalizes large values of σ⊥,∥ and is present to reduce the number of poor optimization results. We have tried the fitting with various values of λreg, and we found that λreg = 10 has no impact on the majority of results, only on the edge cases. Hence this is the value we use.

This process is repeated for every pixel in the field of view, enabling us to create a global two-dimensional map of the correlation length.

Previous estimates of perpendicular correlation length have used autocorrelation functions of spatially separated time series32. The structure of the autocorrelation function was modelled with an exponential function, and the perpendicular correlation length is given as the 1/e length. Hence to compare the estimated values of σ⊥ to previous estimates, we are required to multiply by a factor of \(\sqrt{2}\), that is, \({L}_{\perp }=\sqrt{2}{\sigma }_{\perp }\).

Kernel density estimation

The probability distribution of the measured perpendicular correlation length scales (Fig. 2) are estimated via kernel density estimation67. Mathematically, the kernel density estimator at a point x within a group of data Xi; i = 1 … n, can be described as

$${{\varPsi }}(x)=\frac{1}{nh}\mathop{\sum }\limits_{i=1}^{n}K\left(\frac{{X}_{i}-x}{h}\right)$$
(13)

where, K(x) is the kernel function for a given bandwidth h > 0. Here the choice of bandwidth (h) is an important factor to determine the accuracy of the density estimate for the data. This parameter controls the balance between bias and variance associated with the estimator, regulating the under-smoothing and over-smoothing of the probability density estimates. To find the best bandwidth for the data, we use hyperparameter tuning via cross-validation67. This is a powerful technique that is capable of providing estimates for the so-called test error; hence, it is used to prevent under- or over-fitting of the model via selection of the hyperparameter(s) that provide the lowest estimated test error. We used fivefold cross-validation to select the bandwidth. In this approach, the original dataset is split into five partitions and the probability density is estimated using four of the five partitions for each considered value of bandwidth. The estimated test error is than calculated on the remaining partition. This is performed five times, using a different partition each time for calculating the estimate of the test error. The average test error among the five trials is calculated and the value of bandwidth with the lowest estimated test error is the most appropriate hyperparameter for the given dataset. The best choice of bandwidth is then implemented to calculate the probability density for the original (entire) dataset.

Theoretical models for perpendicular correlation length

In Fig. 3, we show the expected evolution of perpendicular correlation length from theoretical models. The data for the theoretical curves are provided by Steven Cranmer and was first discussed in ref. 48. Here we provide a brief discussion for context.

The evolution of the perpendicular correlation length parameter (L⊥) from the solar photosphere to the near-Earth space environment (~215.6 R⊙) are modelled using assumptions regarding the background magnetic-field (B0) expansion and contributions from confined Alfvénic fluctuations therein. A simple model (M1) for the correlation length describes its evolution only as a function of the magnetic-field strength, that is

$${L}_{\perp }\propto {B}_{0}^{-1/2},$$
(14)

to account for flux tube expansion in the solar atmosphere49. This approximation relied on the fact that flux tubes acts as independent channels for pure Alfvén waves that propagate along the background magnetic fields. As the wave guides are assumed to be independent, the separation between magnetic flux tubes (or their cross-sectional widths) is taken as the measure of the correlation lengths. However, this approximation does not hold as there is coupling between the Alfvénic waves with other wave mode(s) and flows.

The transport equation, M1, can be further developed by including contributions from the nonlinear coupling between the Alfvénic waves and the background plasma flow properties48. The revised transport equation (M2) describes the radial evolution of L⊥ as:

$$\frac{\partial {L}_{\perp }}{\partial r}=\frac{{L}_{\perp }}{2{A}_{0}}\frac{\partial {A}_{0}}{\partial r}+\frac{\tilde{{\beta }_{A}}}{{u}_{0}+{V}_{A}}\left(\frac{{Z}_{-}^{\,2}{Z}_{+}+{Z}_{+}^{\,2}{Z}_{-}}{{Z}_{-}^{\,2}+{Z}_{+}^{\,2}}\right)$$
(15)

where, \({\tilde{\beta }}_{A}\) (akin to \({\tilde{\alpha }}_{A}/2\) from ref. 68) is the von Kármán constant that serves as a free parameter to match the dissipation rates in numerical simulations to heliospheric observables. Here A0 and VA are the cross-sectional area of the magnetic flux tube (A0 ∝ 1/B0) and Alfvén velocity respectively, and u0 is the magnitude of solar wind outflow speed. The subscript 0 refers to time-averaged magnitudes of the parameters. The terms Z± represent Elsasser variables69, which are the sum of plasma and Alfvénic fluctuations and can be expressed as

$${Z}_{\pm }={V}_{y}\pm \frac{{B}_{y}}{\sqrt{4\uppi {\rho }_{0}}}$$
(16)

where, the subscript y refers to the plasma and magnetic-field fluctuations in the direction perpendicular to background magnetic field, which is restricted along the z direction in a Cartesian coordinate system.