Abstract
The heavy element abundance profiles of galaxies place stringent constraints on galaxy growth and assembly history. As the Milky Way is currently the only spiral galaxy in which we can measure temporally resolved chemical abundances, it enables insights into the origin of metallicity gradients and their correlation with the growth history of galaxies. However, until now, these abundance profiles have not been translated into the integrated-light measurements that are needed to compare the Milky Way with the general galaxy population. Here we report the measurement of the light-weighted, integrated stellar metallicity profile of our Galaxy. We find that the integrated stellar metallicity profile of the Milky Way has a ∧-like broken shape, with a mildly positive gradient inside a Galactocentric radius of 7 kpc and a steep negative gradient outside. This broken integrated metallicity profile of the Milky Way is not unique but is not common among Milky Way-mass star-forming galaxies observed in the MaNGA survey and simulated in the TNG50 cosmological simulation. Our results suggest that the Milky Way might not have a typical metallicity distribution for a galaxy of its mass, and thus offers valuable insight into the rich variety of galaxy enrichment processes.
Similar content being viewed by others
Main
Our home galaxy, the Milky Way, provides unique and strict constraints to galaxy formation and evolution because of the detailed, temporally resolved observations that we can obtain from individual stars. However, the integrated properties of the Milky Way are poorly understood, and this limits a detailed comparative analysis of the properties of the Milky Way in the context of the general galaxy population, for the vast majority of which only integrated properties are measurable.
With the recent advent of massive spectroscopic surveys, which are mapping millions of stars across the Galaxy, direct measurements of integrated stellar population properties (for example, elemental abundances) of the Milky Way are becoming possible. In this work, we present the measurement of the radial integrated stellar metallicity profile of our Galaxy, carefully accounting for the selection function of the data, and perform direct comparison with other similar-mass, star-forming galaxies both in the local Universe and in cosmological simulations of galaxy formation.
We determine the integrated stellar metallicity (traced by the abundance of iron as defined by \([{\rm{Fe}}/{\rm{H}}]=\log \left(\frac{{N}_{\rm{Fe}}/{N}_{\rm{H}}}{\rm{N}_{{\rm{Fe}}_{\odot }}/{N}_{\rm{H}_{\odot }}}\right)\), where NFe/NH is the number ratio between iron and hydrogen in a given star and NFe⊙/NH⊙ is that ratio in the Sun) profiles from 2 to 15 kpc of the Milky Way by using chemical abundances, ages and distances of individual stars derived from spectra observed with APOGEE1 and astrometric data from Gaia2. We transform the observations from a sample of targeted stars to the intrinsic, entire stellar population by correcting for the survey selection function for stars of different abundances separately. The obtained luminosity density distribution of intrinsic populations of different abundances is then used to calculate the light-weighted average stellar metallicity (Methods).
When accounting for stars of all ages, the light-weighted integrated stellar metallicity of the Milky Way is overall subsolar. The radial profile of the integrated stellar metallicity shows a break at 6.9 ± 0.6 kpc, with a positive slope of 0.031 ± 0.010 dex kpc−1 within the break radius and a negative slope of −0.052 ± 0.008 dex kpc−1 beyond it (Fig. 1 and Methods). This break, however, is not seen in the metallicity profiles of mono-age populations, which are either flat in the old age bin, or steep and negative in younger stellar populations. The steep gradient of young populations is consistent with observations of young stars and H ii regions in the Milky Way3,4,5,6,7,8,9. The fraction of total luminosity in the old (8–12 Gyr), metal-poor stellar population decreases with radius, while the opposite is true for the younger, more metal-rich populations. This is consistent with the more radially compact structure, that is shorter scale length, of the old population10,11. This radially varying contribution of the old, metal-poor versus young, metal-rich stellar populations in the disk gives rise to the positive slope of metallicity profile in the inner Galaxy12. For the same reason, the negative slope in the outer Galaxy reflects the gradient of the young and intermediate-age populations that dominate at larger radii. These results suggest an intriguing connection between the integrated stellar metallicity profile and the structural evolution of the Milky Way.
The integrated metallicity of all ages and that in each age bin are average values of 26 MAPs, weighted by their bolometric luminosity (Methods). Error bars and shaded regions indicate the 1σ uncertainties of the average metallicity measurements. The sizes of the coloured squares indicate the fraction of the total luminosity for each radial bin contained in each mono-age component.
To compare the Milky Way with other galaxies, we measure the integrated stellar and gas-phase metallicity profiles of 321 face-on, star-forming galaxies with Milky Way-like stellar mass (|log(M★/MMW)| < 0.2 dex) in the MaNGA (Mapping Nearby Galaxies at Apache Point Observatory) Integral Field Unit (IFU) survey13 (Methods). In addition, we compare our results with profiles of 134 Milky Way-mass, star-forming galaxies in the TNG50 cosmological magnetohydrodynamical simulation14,15. Figure 2 shows the total (that is, average stellar, left and middle panels) and present-day (that is, gas-phase or young stars, right panel) metallicity profiles of these MaNGA and TNG50 galaxies in comparison with that of the Milky Way. All profiles are normalized to their galaxy’s effective radius (Re) to marginalize over the effect of galaxy size. Because of uncertainty in the current measurement of the Milky Way’s size (Methods), we adopt a range of effective radii of 3.4–6.7 kpc (ref. 16) for the Milky Way, corresponding to a scale length of 2–4 kpc assuming a single-exponential profile; we thus show the Milky way’s metallicity profiles for the two extreme cases. It is evident that, regardless of the Milky Way’s size, the integrated metallicity profiles of our Galaxy are inconsistent with the bulk of Milky Way-mass MaNGA and TNG50 galaxies, which—when averaged across the populations—generally show flatter radial metallicity distributions. The flatter stellar metallicity gradients of local galaxies are qualitatively consistent with other independent measurements of MaNGA galaxies17 and different IFU surveys18, and are also consistent with those of nearby massive star-forming galaxies19,20,21,22, for which spectroscopic observations of resolved luminous stellar populations (for example, red or blue supergiants) are available.
The blue and magenta shaded regions represent the mean ± s.d. of the distributions of 321 MaNGA galaxies and 134 TNG50 galaxies, respectively. The filled symbols and error bars denote their median metallicity profile and the error of the median. Left: average radial light-weighted stellar metallicity profile of the Milky Way (black and grey) in comparison with those of low-redshift Milky Way-mass star-forming galaxies in the MaNGA survey (blue). Light-blue curves denote the profiles of individual MaNGA galaxies in our sample. One example galaxy that shows a Milky Way-like broken profile is highlighted with a thickened line. Given the uncertainty of the Milky Way’s size, we adopt two values of 3.4 and 6.7 kpc to illustrate the range of the Milky Way’s profile normalized to the effective radius. Middle: the same as the left but showing the comparison with galaxies from the TNG50 simulation (magenta). As on the left, an example galaxy with a similarly broken profile is highlighted. Right: comparison among the same galaxy samples as on the left and in the middle but for their present-day metallicity gradients. For MaNGA galaxies, we use the oxygen abundance ([O/H]) measured in their ionized gas from optical emission lines (Methods) to represent their present-day metallicity. For the Milky Way and TNG50 galaxies, we use the [Mg/H], which is tightly correlated with [O/H] (ref. 95), of their young (0–4 Gyr) stellar populations to represent their present-day metallicity (Methods).
Although appearing to be uncommon, the broken stellar metallicity profile of the Milky Way is not unique in either the observed or simulated samples or in other local observations23. To estimate the frequency of the Milky Way-like profile in these samples, we quantify the inner and outer gradients of the metallicity profiles of individual MaNGA and TNG50 galaxies with a broken linear function, the same as that of the Milky Way (Methods). We find a small fraction of the comparison galaxies (~1% in the MaNGA sample and 11% in the TNG50 sample) that have normalized inner and outer gradients (in dex Re−1) consistent with those of the Milky Way within uncertainties, including the uncertainties due to the Milky Way’s size. We highlight one such galaxy in each sample in Fig. 2. We note that the fraction in our MaNGA sample might be underestimated because of limited spatial resolution and radial coverage of the data.
Regarding the present-day metallicity profiles, Milky Way-like galaxies generally show a monotonic, negative gradient, qualitatively consistent with the Milky Way. Quantitative comparison of the gradient normalized to the effective radius, however, is rather sensitive to the adopted size of our Galaxy. The metallicity gradients of galaxies are comparable to that of the Milky Way when assuming a small size of our Galaxy, but tend to be flatter than the Milky Way when a larger size is adopted.
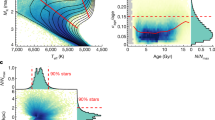
The analysis of the simulated galaxies confirms that there is an innate relationship between the shape of the galaxy metallicity profiles and the disk structure evolution, as shown in Figure 3. In the inner regions (Fig. 3a), the Milky Way and TNG50 galaxies with Milky Way-like disk structure evolution show a positive metallicity gradient accompanied by a positive gradient of the luminosity profile of the young population. This indicates reduced recent star formation in the innermost regions of these galaxies, and could be a manifestation of the growth of the bulge24 or of inside-out quenching of star formation25,26,27, possibly due to active galactic nucleus feedback as is the case for TNG50 galaxies15,28,29.
a,b, The disk structure evolution is quantified as the difference between the slope of radial luminosity surface density profiles (Δ log(ΣL)/ΔR) of young (0–4 Gyr) and old (8–12 Gyr) stellar populations, inside (a) and outside (b) the break radius identified in the metallicity radial profiles. Filled circles denote Milky Way-mass, star-forming galaxies in the TNG50 simulation, colour-coded by their effective radius. Two insets on the left-hand side of each panel illustrate the luminosity surface density profiles of young and old populations in two example TNG50 galaxies (black squares): one with strong evolution at the top and one with nearly parallel growth (a) or inverse evolution (young population being more compact, b) at the bottom. The possible position of the Milky Way in these two diagrams is denoted by a shaded ellipse, which is stretched by the large uncertainty on the Milky Way’s effective radius, due in turn to uncertainties in the disk scale length measurement and to the possible deviation from a single-exponential density profile. We adopt the same range of effective radius of our Galaxy as in Fig. 2 and assume equally likely values within this range.
In the outer regions (Fig. 3b), however, TNG50 galaxies with Milky Way-like structure typically show a flatter metallicity gradient. As suggested from empirical chemical evolution models or zoom-in simulations, a steep outer metallicity gradient could possibly be induced by a number of processes: inside-out ignition of star formation due to decreasing gas density with radius and inside-out disk growth due to increasing gas accretion timescale with radius12,30, radial gas inflow along the disk that carries enriched material inwards31,32 and an abrupt, metal-free gas accretion event via, for example, a minor merger that preferentially dilutes the disk at larger radii33,34. The simulated galaxies’ metallicity gradients shaped by these processes may also depend on how they are implemented in the models. For instance, in the metal-free gas accretion scenario, the resulting dilution as a function of radius strongly depends on the radial distribution of gas infall and therefore the mass and orbit of the infalling satellite. These requirements on the infalling-satellite parameters could make the accretion-induced steep metallicity gradient uncommon.
To summarize, we find that the integrated, light-weighted metallicity profile of the Milky Way is non-monotonic, with a positive gradient inside 7 kpc and a negative gradient outside. This metallicity profile is not unique but is uncommon among Milky Way-mass star-forming galaxies both in the local Universe and in a state-of-the-art cosmological simulation. The overall shape of the Milky Way’s gradient is set by the temporal evolution of its inner and outer disk components. The chemical structure of the inner galaxy can be explained by the growth of the bulge or by inside-out quenching of star formation in the inner regions. The structure of the outer regions of the Milky Way, however, is more challenging to explain in the accepted galaxy-formation framework, as the steep metallicity outer profile, combined with the current estimate of the effective radius, makes our Galaxy an atypical system compared with the observed and simulated Milky Way-like galaxy samples. This discrepancy may point either to the erroneous measurement of the Galactic disk size, which may be addressed with upcoming surveys such as WEAVE, the 4-metre Multi-Object Spectroscopic Telescope and the Sloan Digital Sky Survey V (SDSS-V), or to an uncommon physical process operating during the evolution of the Milky Way.
Methods
Data
This work is based on the data from the last internal data release of the APOGEE survey after the SDSS-IV Data Release 16 (refs. 35,36,37). APOGEE is a massive near-infrared, high-resolution spectroscopic survey1 that provides robust and precise stellar parameters and elemental abundances for more than a half million stars, mainly red giant branch stars, in nearly 1,000 discrete fields that are semiregularly distributed throughout the Galactic disk, bulge and halo38,39,40,41. The observed sample is randomly selected, on a field-to-field basis, from candidates defined in the 2MASS H–(J − Ks)0 colour–magnitude diagram. The stellar spectra are obtained using custom spectrographs42 with the 2.5 m Sloan telescope and the New Mexico State University 1 m telescope at the Apache Point Observatory43,44, and with the 2.5 m Irénée du Pont telescope at Las Campanas Observatory45. The spectra are reduced and chemical abundances (for example, [Fe/H], [Mg/Fe]) and stellar parameters (for example, surface gravity and effective temperature) of individual stars are produced by custom pipelines using a new custom line list (the APOGEE Stellar Parameter and Chemical Abundances Pipeline)46,47,48. The stellar ages and spectrophotometric distances are derived by applying the astroNN deep-learning code to the spectroscopic data from APOGEE and astrometric data from Gaia, and are provided in the astroNN Value Added Catalog with typical age uncertainties of 30% and distance uncertainties of 10% (refs. 49,50).
We have corrected the APOGEE abundances of Fe and Mg for the effects of non-local thermodynamic equilibrium (NLTE). This physical process is not captured by standard LTE models and is often taken into account explicitly51. We used the Fe and Mg NLTE model atoms developed by Bergemann et al.52,53. NLTE corrections were calculated for a grid of stellar model atmospheres covering the stellar parameter space of APOGEE observations for individual Mg i and Fe i lines, which are detectable in the H-band APOGEE spectra54. The NLTE abundance corrections are typically within ±0.10 dex for Fe and Mg abundances in individual stars, but they amount to less than 0.02 dex for the integrated light-weighted abundances. Corrections for the NLTE effect change the metallicity gradient only by less than 2%.
Integrated light-weighted metallicity measurements
The integrated stellar metallicity in the Milky Way is derived using the density distribution of mono-abundance populations (MAPs) after carefully correcting for the APOGEE survey selection function55. The process of correcting for the APOGEE selection function is described in greater detail by Lian et al.55, but in summary, using PARSEC isochrones56 and the combined three-dimensional (3D) extinction map57, we estimate the probability that a star, at a given Galactic position and [Fe/H] and [Mg/Fe] abundances, would be selected as a candidate and then eventually observed. The observed number density of APOGEE stars at this position and abundance, divided by this observational probability, gives rise to the local density of the underlying population. This conversion from sampled to intrinsic number density is conducted for all individual MAPs at different Galaxy positions independently. We consider MAPs in the range of abundance where the vast majority of the Milky Way’s stars are located: [Fe/H] between −0.9 and +0.5, with bin width of 0.2 dex, and [Mg/Fe] between −0.1 and 0.4, with bin width of 0.1 dex. The luminosity density of each MAP is then obtained by sampling the PARSEC isochrones assuming a Kroupa initial mass function58. In total, we obtain 3,056 individual luminosity measurements for each MAP spanning Galactocentric radii of 0–25 kpc and vertical distances of 0–14 kpc.
With the 3D luminosity density distribution, we first obtain the luminosity surface density of each MAP as a function of radius by integrating the density distribution in the vertical direction. We bin the density measurements of MAPs into a series of narrow radial bins, from 0 to 15 kpc with bin width of 1 kpc. For each radial bin, we fit the vertical density distribution with a single exponential profile and derive the surface luminosity density by integrating the best-fitted density model. These surface luminosity densities are used to weight each MAP to measure the average light-weighted metallicity of the Milky Way. These values then have the same physical meaning as unresolved stellar metallicity measurements in external galaxies and therefore allow direct comparison between them. The average light-weighted metallicity is calculated via
where σL,i indicates the luminosity surface density of MAP i, and [Fe/H]i denotes the iron abundance of that MAP. The same calculation is performed to obtain the light-weighted magnesium abundance ([Mg/H]), used in the comparison with the gas-phase metallicity of galaxies, which is usually represented by oxygen abundance ([O/H]). The calculation is performed in the radial range 2–15 kpc, where the vertical structures of all dominant MAPs are well determined. The stochastic uncertainty of the integrated metallicity is estimated through Monte Carlo simulations, considering uncertainties of abundances of each MAP and of the obtained surface mass density that are propagated from number density errors at each spatial position. As a conservative estimate, we assume the uncertainties of [Fe/H] and [Mg/Fe] in each MAP to be 0.1 and 0.05 dex, respectively, which are half of the bin widths used for MAP definition.
Since the radial metallicity distribution in the Milky Way varies systematically with height from the disk plane59,60,61,62,63, correcting the survey selection function is essential to derive the unbiased integrated average stellar metallicity and its radial distribution. However, the main result of this paper—that is, that the Milky Way presents a metallicity profile with a pronounced break—is not strongly dependent on the correction for the selection function. The radial metallicity profiles obtained using APOGEE data without accounting for the selection function show similar behaviour to those corrected for the selection function (Supplementary Fig. 1 versus Fig. 1), with a clear break at r ~ 6 kpc, a positive gradient inside the break radius and a strong negative gradient outside. This rough consistency is because of the semiregular layout of APOGEE fields on and off the disk plane, which minimizes the geometric selection effect. However, both the inner and outer gradients are steeper than the integrated stellar metallicity. This suggests that our results are robust against uncertainties in the correction for survey selection function, but such correction is necessary for an accurate understanding of the average metallicity distribution in the Milky Way.
Metallicity profiles in age bins
To investigate the origin of the broken integrated metallicity profile in the Galaxy, we study the metallicity profiles of stars at different ages. These time-resolved metallicity profiles are obtained by first unfolding the number density of each MAP at a given position along the age dimension using the observed age distribution. Then, for each age bin, we perform the same analysis as above to derive the surface luminosities of MAPs and light-weighted average metallicity as a function of radius. Considering age uncertainties of ~30%, we consider three broad age bins from 0 to 12 Gyr with even steps of 4 Gyr.
We are not able to account for the selection function and then calculate the intrinsic density for a given mono-abundance and mono-age bin if none of these stars are observed. Since very young stars (age < 0.5 Gyr) have a very small fraction evolving through the RGB phase and there are possibly no such young stars observed by APOGEE, the contribution of very young populations in the luminosity and average metallicity of total populations in this work is possibly underestimated at all radii. We have performed tests in which we manually increase the luminosity density of the youngest age bin (0–2 Gyr; a broader age bin of 4 Gyr is adopted in the main paper) in our calculations and found that this does not affect our results significantly. A factor of two change in the luminosity of the youngest age bin is a conservative estimate given that only very young stars are possibly missing: it results in only a <0.02 dex variation in the average metallicity of total populations. Note that since the vertical density distribution and surface density of MAPs are calculated separately, before being combined into the ‘all age’ and ‘mono-age’ bins in Fig. 1, the obtained average metallicity of total populations is not precisely identical to the arithmetic average of mono-age populations.
Measurement of metallicity gradients
To measure the metallicity gradient of the Milky Way, because of the visibly non-monotonic profile, we fit a broken linear function,
to the profile with four free parameters: zero point (b), break radius (Rb) and gradient in- and outside (ain, aout) the break radius. The fit is performed in the radial range 2–15 kpc. The uncertainties of the best-fitted gradients are estimated through Monte Carlo simulations considering the stochastic uncertainty of integrated metallicity measurement for each radial bin. The best-fitted break radius is at 6.9 ± 0.6 kpc. The obtained gradients are in unit of dex kpc−1. The normalized gradient in dex Re−1, however, is subject to large uncertainty because of the rather uncertain size estimate of the Milky Way, originating from significant uncertainty in the Milky Way’s disk scale length16 and the complexity of the disk density profile, which may deviate from a single-exponential shape55,64,65,66.
Comparison sample from the MaNGA survey
We compare our findings of the metallicity profiles of the Milky Way with those of similar-mass, star-forming galaxies from the SDSS-IV MaNGA survey13 and the TNG50 cosmological simulation14,15. Raw MaNGA data are spectrophotometrically calibrated67 and reduced by the Data Reduction Pipeline68. From the final MaNGA Product Launch 11, we select 321 face-on galaxies (axis ratio b/a > 0.5, using a and b from the NSA catalogue69) with a specific star formation rate of >10−11 yr−1 (using the total star formation rate measurement from the Max-Planck-Institut für Astrophysik–Johns Hopkins University catalogue70) and |log(M★/MMW)| < 0.2 dex, assuming log(MMW/M☉) = 10.76 (ref. 71). Among them, 256 galaxies are in the Primary+ sample that are observed out to 1.5 Re and 249 galaxies are in the Secondary sample observed out to 2.5 Re.
We take stellar metallicities in each galaxy from the Firefly MaNGA Value-Added Catalogue72,73,74, which uses the Firefly full-spectrum fitting code75 and the MaStar stellar library76,77. Note that because the MaStar stellar library only considers solar α abundance, the derived stellar metallicity is comparable to the iron abundance [Fe/H].
The spaxels of each galaxy are binned using a Voronoi tessellation to ensure a minimum spectrum signal-to-noise ratio of 10 (ref. 78). We require each Voronoi-binned cell to have an uncertainty of stellar metallicity measurement less than 0.5 dex. We notice that the derived radial profiles of MaNGA galaxies may be slightly flatter than the intrinsic ones due to insufficient spatial sampling79. Therefore the fraction of Milky Way-like metallicity profiles in local galaxies might change quantitatively in a different IFU survey but probably not qualitatively. For instance, no clear signature of broken metallicity profiles is seen in massive late-type galaxies in the Calar Alto Legacy Integral Field Area IFU Survey18, which has a higher spatial resolution than MaNGA. A more detailed and comprehensive comparison using spatially resolved extragalactic observations of different spatial resolutions is needed to accurately quantify the frequency of Milky Way-like profiles in the local Universe, which is however beyond the scope of this paper.
MaNGA spectra have a wavelength range between 3,800 and 10,000 Å. We have performed a test to calculate the average metallicity profile of the Milky Way using r-band instead of bolometric luminosity and found consistent results.
Comparison sample from the TNG50 simulation
To compare the Milky Way results with those from current galaxy-formation models, we select Milky Way-like galaxies in the TNG50 simulation by applying the same selection criteria (that is, stellar mass and specific star formation rate cuts) as used for the MaNGA survey. TNG50 returns 134 galaxies satisfying these criteria at the z = 0 snapshot.
TNG50 is a cosmological magnetohydrodynamical simulation for the formation and evolution of galaxies that encompasses a volume of about 50 comoving megaparsecs, thus it samples many thousands of galaxies above 108 M⊙, across galaxy types and environments14,15. In the simulation, processes such as density-threshold star formation, stellar evolution, chemical enrichment, galactic winds generated by supernova explosions, gas cooling and heating, and seeding, growth and feedback from supermassive black holes are all simultaneously followed80,81, with an average mass and spatial resolution in the star-forming galaxies of 8.5 × 104 M⊙ and 50–200 pc, respectively14,29. The TNG50 galaxies at z = 0 have been shown to have structures and properties that are overall consistent with many observational findings: of relevance for the purposes of this comparison, these include the gas-phase metallicity gradients82, the radial star formation rate surface density profiles in comparison with MaNGA galaxies83 and the stellar sizes and overall stellar morphologies in comparison with SDSS data and others84. All this allows us to compare the case of the Milky Way with a relatively large set of simulated and reasonably realistic galaxies.
Following the same procedure as for the Milky Way data, we obtain the integrated light-weighted metallicity profiles of the selected TNG50 galaxies and measure their metallicity gradients and break radii by fitting the light-weighted metallicity profiles of stellar particles within ±4 kpc from the mid-plane and in the 3–25 kpc range. As we obtain profiles outwards from 2 kpc for the Galaxy, we apply a similar minimum radius for fitting the profiles of simulated galaxies. Because TNG50 galaxies are generally more extended than the Milky Way, we apply a maximum radius of 25 kpc to cover the simulated galaxies at least out to 2.5 effective radii. For their present-day metallicity gradient, to be consistent with the Milky Way, we use the metallicity gradient of young stars with ages of 0–4 Gyr. The results from these fits are shown in Fig. 3. The effective radii of TNG50 galaxies are measured using the luminosity distribution at the z = 0 snapshot.
Metallicity profiles of gas and young stars
In the main text, we use the metallicity profiles of young stars (0–4 Gyr) in the Milky Way and TNG50 galaxies to represent their present-day metallicity profiles. To verify this approach we compare the metallicity profiles and gradients between the gas and young stars in our TNG50 galaxies (Supplementary Fig. 2). The metallicity profile of young stars closely follows that of gas, although the latter is just slightly steeper by 0.0026 ± 0.0064 dex kpc−1 on average (the gradient is calculated in the 3–25 kpc range). This difference does not affect the comparison in the main text.
For MaNGA galaxies, we measure the gas metallicity of the same cells with stellar metallicity measurements using emission line fluxes produced by the Data Analysis Pipeline85,86. For each cell, we require the signal-to-noise ratio of the strong emission lines ([O ii]λ3,727, 3,729, Hβ, [O iii]λ4,959, 5,007, Hα, [N ii]λ6,584) to be above 5, so that their ratios place the cell in the star-forming region defined by the conventional demarcation line87 in the Baldwin–Phillips–Terlevich diagram88. We correct for the galactic internal extinction using the Balmer decrement method, assuming case B recombination with an intrinsic Hα/Hβ ratio of 2.87 (ref. 89) and a standard Milky Way extinction law90. To account for systematics in gas metallicity measurements between different calibrations, we test four widely used strong-line metallicity calibrations: R23 (([O ii]λ3,727, 3,729 + [O iii]λ4,959, 5,001)/Hβ; ref. 91), N2O2 ([N ii]λ6,584/[O ii]λ3,727, 3,729; ref. 92) and two O3N2 (([O iii]λ4,959, 5,001/Hβ)/([N ii]λ6,584/Hα)) calibrations93,94. The metallicity profiles derived with these calibrations have large differences in absolute metallicity values but roughly consistent radial gradient shapes. We adopt the R23 calibration, which gives an average metallicity profile of our MaNGA sample most consistent with the young populations in the simulated galaxies and the Milky Way, but we emphasize that our qualitative findings do not depend on the choice of calibrator.
Data availability
All data presented in this work are available in a public repository at https://github.com/lianjianhui/Source-data-for-MW-gradient-paper.git.
References
Majewski, S. R. et al. The Apache Point Observatory Galactic Evolution Experiment (APOGEE). Astron. J. 154, 94 (2017).
Gaia Collaborationet al. The Gaia mission. Astron. Astrophys. 595, A1 (2016).
Esteban, C. & García-Rojas, J. Revisiting the radial abundance gradients of nitrogen and oxygen of the Milky Way. Mon. Not. R. Astron. Soc. 478, 2315–2336 (2018).
Lemasle, B. et al. Milky Way metallicity gradient from Gaia DR2 F/1O double-mode cepheids. Astron. Astrophys. 618, A160 (2018).
Bragança, G. A. et al. Radial abundance gradients in the outer Galactic disk as traced by main-sequence OB stars. Astron. Astrophys. 625, A120 (2019).
Arellano-Córdova, K. Z., Esteban, C., García-Rojas, J. & Méndez-Delgado, J. E. The Galactic radial abundance gradients of C, N, O, Ne, S, Cl, and Ar from deep spectra of H ii regions. Mon. Not. R. Astron. Soc. 496, 1051–1076 (2020).
Minniti, J. H. et al. Using classical cepheids to study the far side of the Milky Way disk. I. Spectroscopic classification and the metallicity gradient. Astron. Astrophys. 640, A92 (2020).
Zhang, H., Chen, Y. & Zhao, G. Radial migration from metallicity gradient of open clusters and outliers. Astrophys. J. 919, 52 (2021).
Spina, L., Magrini, L. & Cunha, K. Mapping the Galactic metallicity gradient with open clusters: the state-of-the-art and future challenges. Universe 8, 87 (2022).
Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D. & Meléndez, J. A first constraint on the thick disk scale length: differential radial abundances in K giants at Galactocentric radii 4, 8, and 12 kpc. Astrophys. J. Lett. 735, L46 (2011).
Bovy, J. et al. The spatial structure of mono-abundance sub-populations of the Milky Way disk. Astrophys. J. 753, 148 (2012).
Schönrich, R. & McMillan, P. J. Understanding inverse metallicity gradients in galactic discs as a consequence of inside-out formation. Mon. Not. R. Astron. Soc. 467, 1154–1174 (2017).
Bundy, K. et al. Overview of the SDSS-IV MaNGA Survey: Mapping Nearby Galaxies at Apache Point Observatory. Astrophys. J. 798, 7 (2015).
Pillepich, A. et al. First results from the TNG50 simulation: the evolution of stellar and gaseous discs across cosmic time. Mon. Not. R. Astron. Soc. 490, 3196–3233 (2019).
Nelson, D. et al. First results from the TNG50 simulation: galactic outflows driven by supernovae and black hole feedback. Mon. Not. R. Astron. Soc. 490, 3234–3261 (2019).
Bland-Hawthorn, J. & Gerhard, O. The Galaxy in context: structural, kinematic, and integrated properties. Annu. Rev. Astron. Astrophys. 54, 529–596 (2016).
Boardman, N. et al. Milky Way analogues in MaNGA: multiparameter homogeneity and comparison to the Milky Way. Mon. Not. R. Astron. Soc. 491, 3672–3701 (2020).
González Delgado, R. M. et al. The CALIFA survey across the Hubble sequence. Spatially resolved stellar population properties in galaxies. Astron. Astrophys. 581, A103 (2015).
Kudritzki, R.-P. et al. Quantitative spectroscopy of blue supergiant stars in the disk of M81: metallicity, metallicity gradient, and distance. Astrophys. J. 747, 15 (2012).
Saglia, R. P. et al. Stellar populations of the central region of M 31. Astron. Astrophys. 618, A156 (2018).
Gregersen, D. et al. Panchromatic Hubble Andromeda Treasury. XII. Mapping stellar metallicity distributions in M31. Astron. J. 150, 189 (2015).
Liu, C. et al. A spectroscopic study of blue supergiant stars in Local Group spiral galaxies: Andromeda and Triangulum. Astrophys. J. 932, 29 (2022).
Sánchez-Blázquez, P. et al. Stellar population gradients in galaxy discs from the CALIFA survey. The influence of bars. Astron. Astrophys. 570, A6 (2014).
Rix, H.-W. et al. The poor old heart of the Milky Way. Astrophys. J. 941, 45 (2022).
Wang, E. et al. SDSS-IV MaNGA: star formation cessation in low-redshift galaxies. I. Dependence on stellar mass and structural properties. Astrophys. J. 856, 137 (2018).
Lin, L. et al. SDSS-IV MaNGA: inside-out versus outside-in quenching of galaxies in different local environments. Astrophys. J. 872, 50 (2019).
Hasselquist, S. et al. APOGEE [C/N] abundances across the Galaxy: migration and infall from red giant ages. Astrophys. J. 871, 181 (2019).
Nelson, E. J. et al. Spatially resolved star formation and inside-out quenching in the TNG50 simulation and 3D-HST observations. Mon. Not. R. Astron. Soc. 508, 219–235 (2021).
Pillepich, A. et al. X-ray bubbles in the circumgalactic medium of TNG50 Milky Way- and M31-like galaxies: signposts of supermassive black hole activity. Mon. Not. R. Astron. Soc. 508, 4667–4695 (2021).
Chiappini, C., Matteucci, F. & Romano, D. Abundance gradients and the formation of the Milky Way. Astrophys. J. 554, 1044–1058 (2001).
Schönrich, R. & Binney, J. Chemical evolution with radial mixing. Mon. Not. R. Astron. Soc. 396, 203–222 (2009).
Chen, B. et al. Chemical evolution with radial mixing redux: extending beyond the Solar Neighborhood. Preprint at arXiv https://doi.org/10.48550/arXiv.2204.11413 (2022).
Buck, T. On the origin of the chemical bimodality of disc stars: a tale of merger and migration. Mon. Not. R. Astron. Soc. 491, 5435–5446 (2020).
Lian, J. et al. The age-chemical abundance structure of the Galactic disc—II. α-dichotomy and thick disc formation. Mon. Not. R. Astron. Soc. 497, 2371–2384 (2020).
Blanton, M. R. et al. Sloan Digital Sky Survey IV: mapping the Milky Way, nearby galaxies, and the distant Universe. Astron. J. 154, 28 (2017).
Ahumada, R. et al. The 16th data release of the Sloan Digital Sky Surveys: first release from the APOGEE-2 southern survey and full release of eBOSS spectra. Astrophys. J. Suppl. Ser. 249, 3 (2020).
Jönsson, H. et al. APOGEE data and spectral analysis from SDSS Data Release 16: seven years of observations including first results from APOGEE-South. Astron. J. 160, 120 (2020).
Zasowski, G. et al. Target selection for the Apache Point Observatory Galactic Evolution Experiment (APOGEE). Astron. J. 146, 81 (2013).
Zasowski, G. et al. Target selection for the SDSS-IV APOGEE-2 Survey. Astron. J. 154, 198 (2017).
Beaton, R. L. et al. Final targeting strategy for the SDSS-IV APOGEE-2N survey. Astron. J. 62, 302 (2021).
Santana, F. A. et al. Final targeting strategy for the SDSS-IV APOGEE-2S survey. Astron. J. 162, 303 (2021).
Wilson, J. C. et al. The Apache Point Observatory Galactic Evolution Experiment (APOGEE) spectrographs. Publ. Astron. Soc. Pac. 131, 055001 (2019).
Gunn, J. E. et al. The 2.5 m telescope of the Sloan Digital Sky Survey. Astron. J. 131, 2332–2359 (2006).
Holtzman, J. A., Harrison, T. E. & Coughlin, J. L. The NMSU 1 m telescope at Apache Point Observatory. Adv. Astron. 2010, 193086 (2010).
Bowen, I. S. & Vaughan, J. A. H. The optical design of the 40-in. telescope and of the Irénée DuPont telescope at Las Campanas Observatory, Chile. Appl. Opt. 12, 1430–1434 (1973).
Nidever, D. L. et al. The Data Reduction Pipeline for the Apache Point Observatory Galactic Evolution Experiment. Astron. J. 150, 173 (2015).
García Pérez, A. E. et al. ASPCAP: the APOGEE Stellar Parameter and Chemical Abundances Pipeline. Astron. J. 151, 144 (2016).
Smith, V. V. et al. The APOGEE Data Release 16 spectral line list. Astron. J. 161, 254 (2021).
Mackereth, J. T. et al. Dynamical heating across the Milky Way disc using APOGEE and Gaia. Mon. Not. R. Astron. Soc. 489, 176–195 (2019).
Leung, H. W. & Bovy, J. Deep learning of multi-element abundances from high-resolution spectroscopic data. Mon. Not. R. Astron. Soc. 483, 3255–3277 (2019).
Chaplin, W. J. et al. Age dating of an early Milky Way merger via asteroseismology of the naked-eye star ν Indi. Nat. Astron. 4, 382–389 (2020).
Bergemann, M., Lind, K., Collet, R., Magic, Z. & Asplund, M. Non-LTE line formation of Fe in late-type stars—I. Standard stars with 1D and 〈3D〉 model atmospheres. Mon. Not. R. Astron. Soc. 427, 27–49 (2012).
Bergemann, M. et al. Non-local thermodynamic equilibrium stellar spectroscopy with 1D and 〈3D〉 models. I. Methods and application to magnesium abundances in standard stars. Astrophys. J. 847, 15 (2017).
Souto, D. et al. Chemical abundances of main-sequence, turnoff, subgiant, and red giant stars from APOGEE spectra. I. Signatures of diffusion in the open cluster M67. Astrophys. J. 857, 14 (2018).
Lian, J. et al. The Milky Way tomography with APOGEE: intrinsic density distribution and structure of mono-abundance populations. Mon. Not. R. Astron. Soc. 513, 4130 (2022).
Bressan, A. et al. PARSEC: stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 427, 127–145 (2012).
Bovy, J., Rix, H.-W., Green, G. M., Schlafly, E. F. & Finkbeiner, D. P. On Galactic density modeling in the presence of dust extinction. Astrophys. J. 818, 130 (2016).
Kroupa, P. On the variation of the initial mass function. Mon. Not. R. Astron. Soc. 322, 231–246 (2001).
Hayden, M. R. et al. Chemical cartography with APOGEE: metallicity distribution functions and the chemical structure of the Milky Way disk. Astrophys. J. 808, 132 (2015).
Xiang, M.-S. et al. The evolution of stellar metallicity gradients of the Milky Way disk from LSS-GAC main sequence turn-off stars: a two-phase disk formation history?. Res. Astron. Astrophys. 15, 1209–1239 (2015).
Stanghellini, L. & Haywood, M. Galactic planetary nebulae as probes of radial metallicity gradients and other abundance patterns. Astrophys. J. 862, 45 (2018).
Wheeler, A. et al. Abundances in the Milky Way across five nucleosynthetic channels from 4 million LAMOST stars. Astrophys. J. 898, 58 (2020).
Vickers, J. J., Shen, J. & Li, Z.-Y. The flattening metallicity gradient in the Milky Way’s thin disk. Astrophys. J. 922, 189 (2021).
Bovy, J. et al. The stellar population structure of the Galactic disk. Astrophys. J. 823, 30 (2016).
Mackereth, J. T. et al. The age–metallicity structure of the Milky Way disc using APOGEE. Mon. Not. R. Astron. Soc. 471, 3057–3078 (2017).
Yu, Z. et al. Mapping the Galactic disk with the LAMOST and Gaia red clump sample. VII. The stellar disk structure revealed by the mono-abundance populations. Astrophys. J. 912, 106 (2021).
Yan, R. et al. SDSS-IV/MaNGA: spectrophotometric calibration technique. Astron. J. 151, 8 (2016).
Law, D. R. et al. The Data Reduction Pipeline for the SDSS-IV MaNGA IFU galaxy survey. Astron. J. 152, 83 (2016).
Blanton, M. R., Kazin, E., Muna, D., Weaver, B. A. & Price-Whelan, A. Improved background subtraction for the Sloan Digital Sky Survey images. Astron. J. 142, 31 (2011).
Brinchmann, J. et al. The physical properties of star-forming galaxies in the low-redshift Universe. Mon. Not. R. Astron. Soc. 351, 1151–1179 (2004).
Licquia, T. C., Newman, J. A. & Bershady, M. A. Does the Milky Way obey spiral galaxy scaling relations? Astrophys. J. 833, 220 (2016).
Goddard, D. et al. SDSS-IV MaNGA: spatially resolved star formation histories in galaxies as a function of galaxy mass and type. Mon. Not. R. Astron. Soc. 466, 4731–4758 (2017).
Parikh, T. et al. SDSS-IV MaNGA: the spatially resolved stellar initial mass function in ~400 early-type galaxies. Mon. Not. R. Astron. Soc. 477, 3954–3982 (2018).
Neumann, J. et al. SDSS-IV MaNGA: drivers of stellar metallicity in nearby galaxies. Mon. Not. R. Astron. Soc. 508, 4844–4857 (2021).
Wilkinson, D. M., Maraston, C., Goddard, D., Thomas, D. & Parikh, T. FIREFLY (Fitting IteRativEly For Likelihood analYsis): a full spectral fitting code. Mon. Not. R. Astron. Soc. 472, 4297–4326 (2017).
Maraston, C. et al. Stellar population models based on the SDSS-IV MaStar library of stellar spectra—I. Intermediate-age/old models. Mon. Not. R. Astron. Soc. 496, 2962–2997 (2020).
Yan, R. et al. SDSS-IV MaStar: a large and comprehensive empirical stellar spectral library—first release. Astrophys. J. 883, 175 (2019).
Cappellari, M. & Emsellem, E. Parametric recovery of line-of-sight velocity distributions from absorption-line spectra of galaxies via penalized likelihood. Publ. Astron. Soc. Pac. 116, 138–147 (2004).
Ibarra-Medel, H. J., Avila-Reese, V., Sánchez, S. F., González-Samaniego, A. & Rodríguez-Puebla, A. Optical integral field spectroscopy observations applied to simulated galaxies: testing the fossil record method. Mon. Not. R. Astron. Soc. 483, 4525–4550 (2019).
Weinberger, R. et al. Simulating galaxy formation with black hole driven thermal and kinetic feedback. Mon. Not. R. Astron. Soc. 465, 3291–3308 (2017).
Pillepich, A. et al. Simulating galaxy formation with the IllustrisTNG model. Mon. Not. R. Astron. Soc. 473, 4077–4106 (2018).
Hemler, Z. S. et al. Gas-phase metallicity gradients of TNG50 star-forming galaxies. Mon. Not. R. Astron. Soc. 506, 3024–3048 (2021).
Motwani, B. et al. First results from SMAUG: insights into star formation conditions from spatially resolved ISM properties in TNG50. Astrophys. J. 926, 139 (2022).
Zanisi, L. et al. A deep learning approach to test the small-scale galaxy morphology and its relationship with star formation activity in hydrodynamical simulations. Mon. Not. R. Astron. Soc. 501, 4359–4382 (2021).
Belfiore, F. et al. The data analysis pipeline for the SDSS-IV MaNGA IFU galaxy survey: emission-line modeling. Astron. J. 158, 160 (2019).
Westfall, K. B. et al. The data analysis pipeline for the SDSS-IV MaNGA IFU galaxy survey: overview. Astron. J. 158, 231 (2019).
Kauffmann, G. et al. The host galaxies of active galactic nuclei. Mon. Not. R. Astron. Soc. 346, 1055–1077 (2003).
Baldwin, J. A., Phillips, M. M. & Terlevich, R. Classification parameters for the emission-line spectra of extragalactic objects. Publ. Astron. Soc. Pac. 93, 5–19 (1981).
Osterbrock, D. E. & Ferland, G. J. Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (University Science Books, 2006).
Cardelli, J. A., Clayton, G. C. & Mathis, J. S. The relationship between infrared, optical, and ultraviolet extinction. Astrophys. J. 345, 245 (1989).
Curti, M. et al. The KLEVER Survey: spatially resolved metallicity maps and gradients in a sample of 1.2 < z < 2.5 lensed galaxies. Mon. Not. R. Astron. Soc. 492, 821–842 (2020).
Dopita, M. A., Sutherland, R. S., Nicholls, D. C., Kewley, L. J. & Vogt, F. P. A. New strong-line abundance diagnostics for H ii regions: effects of κ-distributed electron energies and new atomic data. Astrophys. J. Suppl. Ser. 208, 10 (2013).
Pettini, M. & Pagel, B. E. J. [O iii]/[N ii] as an abundance indicator at high redshift. Mon. Not. R. Astron. Soc. 348, L59–L63 (2004).
Marino, R. A. et al. The O3N2 and N2 abundance indicators revisited: improved calibrations based on CALIFA and Te-based literature data. Astron. Astrophys. 559, A114 (2013).
Ting, Y.-S. & Weinberg, D. H. How many elements matter? Astrophys. J. 927, 209 (2022).
Acknowledgements
M.B. and J.L. are supported through the Lise Meitner grant from the Max Planck Society. We acknowledge support by the Collaborative Research Centre SFB 881 (projects A5, A10), Heidelberg University, of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 949173). J.L. acknowledges support by Yunnan Province Science and Technology Department under grants 202105AE160021 and 202005AB160002. A.P. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—project ID 138713538—SFB 881 (‘The Milky Way System’, subprojects A01 and A06). This material is based upon work supported by the National Science Foundation under grant AST-2009993.
Funding for SDSS-IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science and the participating institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University and Yale University.
Funding
Open access funding provided by the Max Planck Society.
Author information
Authors and Affiliations
Contributions
J.L. and G.Z. developed the initial idea. J.L., G.Z. and R.R.L. prepared the APOGEE data. A.P. prepared the TNG50 models. M.B. prepared the NLTE models. J.L., M.B. and A.P. conducted the data analysis. J.L., M.B., A.P. and G.Z. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Astronomy thanks Patricia Sánchez-Blázquez and Fernando Rosales-Ortega for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1 and 2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lian, J., Bergemann, M., Pillepich, A. et al. The integrated metallicity profile of the Milky Way. Nat Astron 7, 951–958 (2023). https://doi.org/10.1038/s41550-023-01977-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-023-01977-z
This article is cited by
-
The broken-exponential radial structure and larger size of the Milky Way galaxy
Nature Astronomy (2024)