Abstract
Solar eruptions are spectacular magnetic explosions in the Sun’s corona, and how they are initiated remains unclear. Prevailing theories often rely on special magnetic topologies that may not generally exist in the pre-eruption source region of corona. Here, using fully three-dimensional magnetohydrodynamic simulations with high accuracy, we show that solar eruptions can be initiated in a single bipolar configuration with no additional special topology. Through photospheric shearing motion alone, an electric current sheet forms in the highly sheared core field of the magnetic arcade during its quasi-static evolution. Once magnetic reconnection sets in, the whole arcade is expelled impulsively, forming a fast-expanding twisted flux rope with a highly turbulent reconnecting region underneath. The simplicity and efficacy of this scenario argue strongly for its fundamental importance in the initiation of solar eruptions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The amount of data generated by the high-resolution 3D MHD simulations and analysed for this paper is approximately 10 TB. Interested parties are invited to contact the corresponding authors to make arrangements for the transfer of those data.
Code availability
We have opted to not make our numerical code of the MHD simulation publicly available owing to its complexity, which demands expert assistance to set up, run and analyse simulations, and because it is continually being improved and extended, which requires frequent software updates. Interested parties are invited to contact the authors for more detailed information.
References
Fleishman, G. D. et al. Decay of the coronal magnetic field can release sufficient energy to power a solar flare. Science 367, 278–280 (2020).
Priest, E. R. & Forbes, T. G. The magnetic nature of solar flares. Astron. Astrophys. Rev. 10, 313–377 (2002).
Forbes, T. G. et al. CME theory and models. Space Sci. Rev. 123, 251–302 (2006).
Shibata, K. & Magara, T. Solar flares: magnetohydrodynamic processes. Living Rev. Sol. Phys. 8, 6 (2011).
Chen, P. F. Coronal mass ejections: models and their observational basis. Living Rev. Sol. Phys. 8, 1 (2011).
Schmieder, B., Démoulin, P. & Aulanier, G. Solar filament eruptions and their physical role in triggering coronal mass ejections. Adv. Space Res. 51, 1967–1980 (2013).
Aulanier, G. The physical mechanisms that initiate and drive solar eruptions. Proc. Int. Astron. Union 8, 184–196 (2014).
Janvier, M., Aulanier, G. & Démoulin, P. From coronal observations to MHD simulations, the building blocks for 3D models of solar flares (invited review). Sol. Phys. 290, 3425–3456 (2015).
Lin, J. et al. Review on current sheets in CME development: theories and observations. Space Sci. Rev. 194, 237–302 (2015).
Kliem, B. & Török, T. Torus instability. Phys. Rev. Lett. 96, 255002 (2006).
Török, T. & Kliem, B. Confined and ejective eruptions of kink-unstable flux ropes. Astrophys. J. Lett. 630, L97–L100 (2005).
Fan, Y. & Gibson, S. E. Onset of coronal mass ejections due to loss of confinement of coronal flux ropes. Astrophys. J. 668, 1232–1245 (2007).
Aulanier, G., Török, T., Démoulin, P. & DeLuca, E. E. Formation of torus-unstable flux ropes and electric currents in erupting sigmoids. Astrophys. J. 708, 314–333 (2010).
Amari, T., Canou, A., Aly, J. -J., Delyon, F. & Alauzet, F. Magnetic cage and rope as the key for solar eruptions. Nature 554, 211–215 (2018).
Antiochos, S. K., DeVore, C. R. & Klimchuk, J. A. A model for solar coronal mass ejections. Astrophys. J. 510, 485–493 (1999).
Aulanier, G., DeLuca, E. E., Antiochos, S. K., McMullen, R. A. & Golub, L. The topology and evolution of the Bastille Day flare. Astrophys. J. 540, 1126–1142 (2000).
Lynch, B. J., Antiochos, S. K., DeVore, C. R., Luhmann, J. G. & Zurbuchen, T. H. Topological evolution of a fast magnetic breakout CME in three dimensions. Astrophys. J. 683, 1192–1206 (2008).
Wyper, P. F., Antiochos, S. K. & DeVore, C. R. A universal model for solar eruptions. Nature 544, 452–455 (2017).
Patsourakos, S. et al. Decoding the pre-eruptive magnetic field configurations of coronal mass ejections. Space Sci. Rev. 216, 131 (2020).
DeVore, C. R. & Antiochos, S. K. Dynamical formation and stability of helical prominence magnetic fields. Astrophys. J. 539, 954–963 (2000).
Wang, H. et al. Witnessing magnetic twist with high-resolution observation from the 1.6-m New Solar Telescope. Nat. Commun. 6, 7008 (2015).
Wang, W. et al. Buildup of a highly twisted magnetic flux rope during a solar eruption. Nat. Commun. 8, 1330 (2017).
Ugarte-Urra, I., Warren, H. P. & Winebarger, A. R. The magnetic topology of coronal mass ejection sources. Astrophys. J. 662, 1293–1301 (2007).
Moore, R. L. & Labonte, B. J. The filament eruption in the 3B flare of July 29, 1973 - Onset and magnetic field configuration. Proc. Int. Astron. Union 91, 207–211 (1980).
Moore, R. L. & Roumeliotis, G. in Lecture Notes in Physics Vol. 399 (eds Švestka Z. et al.) 69–78 (Springer, 1992).
Moore, R. L., Sterling, A. C., Hudson, H. S. & Lemen, J. R. Onset of the magnetic explosion in solar flares and coronal mass ejections. Astrophys. J. 552, 833–848 (2001).
Schrijver, C. J. A characteristic magnetic field pattern associated with all major solar flares and its use in flare forecasting. Astrophys. J. Lett. 655, L117–L120 (2007).
Toriumi, S. & Wang, H. Flare-productive active regions. Living Rev. Sol. Phys. 16, 3 (2019).
Emslie, A. G. et al. Global energetics of thirty-eight large solar eruptive events. Astrophys. J. 759, 71 (2012).
Zhang, J., Dere, K. P., Howard, R. A., Kundu, M. R. & White, S. M. On the temporal relationship between coronal mass ejections and flares. Astrophys. J. 559, 452–462 (2001).
Zhang, J. & Dere, K. P. A statistical study of main and residual accelerations of coronal mass ejections. Astrophys. J. 649, 1100–1109 (2006).
Cheng, X. et al. Initiation and early kinematic evolution of solar eruptions. Astrophys. J. 894, 85 (2020).
Aly, J. J. How much energy can be stored in a three-dimensional force-free magnetic field? Astrophys. J. Lett. 375, L61–L64 (1991).
Sturrock, P. A. Maximum energy of semi-infinite magnetic field configurations. Astrophys. J. 380, 655–659 (1991).
Petschek, H. E. in AAS–NASA Symposium on the Physics of Solar Flares (ed. Hess, W. N.) 425–439 (NASA, 1964).
Linker, J. A. et al. Flux cancellation and coronal mass ejections. Phys. Plasmas 10, 1971–1978 (2003).
Amari, T., Luciani, J. F., Aly, J. J., Mikic, Z. & Linker, J. Coronal mass ejection: initiation, magnetic helicity, and flux ropes. I. Boundary motion-driven evolution. Astrophys. J. 585, 1073–1086 (2003).
Török, T. et al. Sun-to-Earth MHD simulation of the 2000 July 14 Bastille Day eruption. Astrophys. J. 856, 75 (2018).
Wang, H., Qiu, J., Jing, J. & Zhang, H. Study of ribbon separation of a flare associated with a quiescent filament eruption. Astrophys. J. 593, 564–570 (2003).
Hinterreiter, J., Veronig, A. M., Thalmann, J. K., Tschernitz, J. & Pötzi, W. Statistical properties of ribbon evolution and reconnection electric fields in eruptive and confined flares. Sol. Phys. 293, 38 (2018).
Yan, X. L. et al. Successive X-class flares and coronal mass ejections driven by shearing motion and sunspot rotation in active region NOAA 12673. Astrophys. J. 856, 79 (2018).
Bhattacharjee, A., Huang, Y. M., Yang, H. & Rogers, B. Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16, 112102 (2009).
Huang, Y. M. & Bhattacharjee, A. Scaling laws of resistive magnetohydrodynamic reconnection in the high-Lundquist-number, plasmoid-unstable regime. Phys. Plasmas 17, 062104 (2010).
Daughton, W. Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas. Nat. Phys. 7, 539–542 (2011).
Nishida, K., Nishizuka, N. & Shibata, K. The role of a flux rope ejection in a three-dimensional magnetohydrodynamic simulation of a solar flare. Astrophys. J. Lett. 775, L39 (2013).
Mikic, Z. & Linker, J. A. Disruption of coronal magnetic field arcades. Astrophys. J. 430, 898–912 (1994).
Choe, G. S. & Lee, L. C. Evolution of solar magnetic arcades. I. Ideal MHD evolution under footpoint shearing. Astrophys. J. 472, 360–371 (1996).
Amari, T., Luciani, J. F., Aly, J. J., Mikic, Z. & Linker, J. Coronal mass ejection: initiation, magnetic helicity, and flux ropes. II. Turbulent diffusion-driven evolution. Astrophys. J. 595, 1231–1250 (2003).
Karpen, J. T., Antiochos, S. K. & DeVore, C. R. The mechanisms for the onset and explosive eruption of coronal mass ejections and eruptive flares. Astrophys. J. 760, 81 (2012).
Yardley, S. L., Green, L. M., van Driel-Gesztelyi, L., Williams, D. R. & Mackay, D. H. The role of flux cancellation in eruptions from bipolar ARs. Astrophys. J. 866, 8 (2018).
van Ballegooijen, A. A. & Martens, P. C. H. Formation and eruption of solar prominences. Astrophys. J. 343, 971–984 (1989).
Jiang, C. W., Feng, X. S., Zhang, J. & Zhong, D. K. AMR simulations of magnetohydrodynamic problems by the CESE method in curvilinear coordinates. Sol. Phys. 267, 463–491 (2010).
Feng, X. S. et al. Three-dimensional solar wind modeling from the Sun to Earth by a SIP-CESE MHD model with a six-component grid. Astrophys. J. 723, 300–319 (2010).
Jiang, C. W., Wu, S. T., Feng, X. S. & Hu, Q. Data-driven MHD simulation of a flux-emerging active region leading to solar eruption. Nat. Commun. 7, 11522 (2016).
Brown, D. S. et al. Observations of rotating sunspots from TRACE. Sol. Phys. 216, 79–108 (2003).
Yan, X. L. & Qu, Z. Q. Rapid rotation of a sunspot associated with flares. Astron. Astrophys. 468, 1083–1088 (2007).
Yan, X. L., Qu, Z. Q., Kong, D. F. & Xu, C. L. Sunspot rotation, sigmoidal filament, flare, and coronal mass ejection: the event on 2000 February 10. Astrophys. J. 754, 16 (2012).
Amari, T., Luciani, J. F., Aly, J. J. & Tagger, M. Very fast opening of a three-dimensional twisted magnetic flux tube. Astrophys. J. Lett. 466, L39–L42 (1996).
Tokman, M. & Bellan, P. M. Three-dimensional model of the structure and evolution of coronal mass ejections. Astrophys. J. 567, 1202–1210 (2002).
Török, T. & Kliem, B. The evolution of twisting coronal magnetic flux tubes. Astron. Astrophys. 406, 1043–1059 (2003).
DeVore, C. R. & Antiochos, S. K. Homologous confined filament eruptions via magnetic breakout. Astrophys. J. 680, 740–756 (2008).
Shibata, K. & Tanuma, S. Plasmoid-induced-reconnection and fractal reconnection. Earth Planets Space 53, 473–482 (2001).
Priest, E. R. Solar Magneto-Hydrodynamics (Springer, 1987).
Shiota, D., Kusano, K., Miyoshi, T., Nishikawa, N. & Shibata, K. A quantitative MHD study of the relation among arcade shearing, flux rope formation, and eruption due to the tearing instability. J. Geophys. Res. 113, A03S05 (2008).
Jiang, C. et al. How did a major confined flare occur in super solar active region 12192? Astrophys. J. 828, 62 (2016).
Spitzer, L. Physics of Fully Ionized Gas 2nd edn (Interscience, 1962).
Yokoyama, T. & Shibata, K. What is the condition for fast magnetic reconnection? Astrophys. J. Lett. 436, L197–L200 (1994).
Lazarian, A. & Vishniac, E. T. Reconnection in a weakly stochastic field. Astrophys. J. 517, 700–718 (1999).
Kowal, G., Lazarian, A., Vishniac, E. T. & Otmianowska-Mazur, K. Numerical tests of fast reconnection in weakly stochastic magnetic fields. Astrophys. J. 700, 63–85 (2009).
Aulanier, G., Janvier, M. & Schmieder, B. The standard flare model in three dimensions. I. Strong-to-weak shear transition in post-flare loops. Astron. Astrophys. 543, A110 (2012).
Janvier, M., Aulanier, G., Pariat, E. & Démoulin, P. The standard flare model in three dimensions. III. Slip-running reconnection properties. Astron. Astrophys. 555, A77 (2013).
Inoue, S., Hayashi, K., Shiota, D., Magara, T. & Choe, G. S. Magnetic structure producing X- and M-class solar flares in solar active region 11158. Astrophys. J. 770, 79 (2013).
Savcheva, A. et al. The relation between solar eruption topologies and observed flare features. II. Dynamical evolution. Astrophys. J. 817, 43 (2016).
Liu, R. et al. Structure, stability, and evolution of magnetic flux ropes from the perspective of magnetic twist. Astrophys. J. 818, 148 (2016).
Duan, A. et al. A study of pre-flare solar coronal magnetic fields: magnetic flux ropes. Astrophys. J. 884, 73 (2019).
Titov, V. S., Hornig, G. & Démoulin, P. Theory of magnetic connectivity in the solar corona. J. Geophys. Res. 107, 1164 (2002).
Berger, M. A. & Prior, C. The writhe of open and closed curves. J. Phys. A 39, 8321–8348 (2006).
Qiu, J., Lee, J., Gary, D. E. & Wang, H. M. Motion of flare footpoint emission and inferred electric field in reconnecting current sheets. Astrophys. J. 565, 1335–1347 (2002).
Jiang, C. et al. Magnetohydrodynamic simulation of the X9.3 flare on 2017 September 6: evolving magnetic topology. Astrophys. J. 869, 13 (2018).
Qiu, J., Longcope, D. W., Cassak, P. A. & Priest, E. R. Elongation of flare ribbons. Astrophys. J. 838, 17 (2017).
Su, Y., Golub, L. & Van Ballegooijen, A. A. A statistical study of shear motion of the footpoints in two-ribbon flares. Astrophys. J. 655, 606–614 (2007).
Démoulin, P., Priest, E. R. & Lonie, D. P. Three-dimensional magnetic reconnection without null points 2. Application to twisted flux tubes. J. Geophys. Res. 101, 7631–7646 (1996).
Savcheva, A., Pariat, E., van Ballegooijen, A., Aulanier, G. & DeLuca, E. Sigmoidal active region on the Sun: comparison of a magnetohydrodynamical simulation and a nonlinear force-free field model. Astrophys. J. 750, 15 (2012).
Janvier, M. Electric currents in flare ribbons: observations and three-dimensional standard model. Astrophys. J. 788, 60 (2014).
Jing, J. et al. Unprecedented fine structure of a solar flare revealed by the 1.6 m New Solar Telescope. Sci. Rep. 6, 24319 (2016).
Acknowledgements
C.W.J. acknowledges support from National Natural Science Foundation of China (NSFC) grants 41822404 and 41731067, the Fundamental Research Funds for the Central Universities (grant No. HIT.BRETIV.201901), and Shenzhen Technology Project JCYJ20190806142609035. X.S.F. is supported by NSFC grants 42030204, 41861164026 and 41874202 and the Strategic Priority Program of the Chinese Academy of Sciences, grant No. XDB41000000. R.L. is supported by NSFC grants 41774150 and 11925302 and the Strategic Priority Program of the Chinese Academy of Sciences, grant No. XDB41030100. X.L.Y. is supported by NSFC grant 11873087, Yunnan Science Foundation for Distinguished Young Scholars, grant No. 202001AV070004 and the Yunnan Key Science Foundation of China, grant No. 2018FA001. Data from observations are courtesy of NASA SDO and STEREO. The computational work was carried out on TianHe-1(A), National Supercomputer Center in Tianjin, China.
Author information
Authors and Affiliations
Contributions
C.W.J. conceived the study, developed the numerical MHD model, performed the analysis and wrote the text. X.S.F. contributed to the design of numerical MHD schemes. R.L., X.L.Y., Q.H., R.L.M. and A.Y.D. contributed to the analysis. All authors participated in discussions and revisions to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Astronomy thanks Guillaume Aulanie and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Some key parameters for the settings of the simulation.
a, Magnetic flux distribution and surface rotation flow at the bottom surface (that is, z = 0). The background is color-coded by the vertical magnetic component Bz, and the vectors show the rotation flow. b, Profile of velocity (the black line) and its ratio to local Alfvén speed (the red line) along (x, z) = 0 line. c, Plasma β (that is, ratio of gas pressure to the magnetic pressure) profile along the central vertical line, that is, (x, y) = 0. d, Profile of Alfvén speed along the central vertical line. In (c) and (d), the black lines are shown for the initial values, while the red lines represent the values at time immediately prior to the eruption onset.
Extended Data Fig. 2 Magnetic field, current density and decay index around the eruption onset.
a, Current density on the slice of x = 0 at the time when the MFR first forms during the eruption (that is, t = 221 min 33 s). The black curves are projection of magnetic field lines on the slice. The lower arrow denotes the axis of the MFR. The upper arrow denotes the critical height of torus instability (TI). b, From top to bottom are shown for current density, magnetic field component By, and decay index of By, respectively, along z axis (that is, the line with both x and y = 0). The black, magenta, and blue curves represent results for the initial potential field (t = 0), the field immediately prior to the eruption onset (t = 217 min), and the field at t = 221 min 33 s, respectively. In the middle panel, the thick vertical line colored in gray denotes the height at which the MFR is initially formed. In the bottom panel, the dashed horizontal line denotes the critical value (1.5) of decay index, and the dashed vertical lines denote the corresponding heights.
Extended Data Fig. 3 The fully opened magnetic field discretized on grid with resolution of 90 km.
a, Current density distribution on the central cross section, that is, the x = 0 slice, showing that current only distributes in the central line, or more exactly a current sheet with a finite thickness of 90 km, while all other regions are current-free. The black curves represent the magnetic field lines, which are fully opened, that is, extending from the bottom surface to infinity. b, Profile of current density along z axis.
Extended Data Fig. 4 Parameters that are comparable with observations.
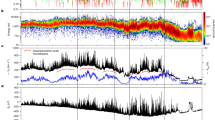
a, Current distribution on the central cross section. b, A time stack map of the current distribution around x, y = 0, which can reveal the evolution speed of the CME. c, Temporal evolution of the edge of the post-flare loops. d, Rising of the post-flare loop top. e, Horizontal motion of the post-flare loop footpoints, which corresponds to the separation of flare ribbons. The dashed lines in (d) and (e) denote the average speeds of the motions.
Extended Data Fig. 5 Mini flux ropes formed in the reconnecting CS.
The field lines are colored differently and the bottom surface is shown with the magnetic flux distribution.
Supplementary information
Supplementary Information
Supplementary Figs. 1–11 and captions for Videos 1–10.
Supplementary Video 1
Animation for Fig. 1.
Supplementary Video 2
Formation of CS and onset of reconnection and eruption: comparison of runs with increasing resolutions (also an animation for Fig. 2). (A) Central vertical slice of current density J. (B) same as (A) and overlaid with 2D field lines on the plane. (C) Velocity on the plane. The arrows show the flow directions and the background shows the vertical component of the flow. The largest Alfvénic Mach number is denoted. (D) Evolution of changing rates of magnetic and kinetic energies. The vertical blue line denotes the time for which all other panels are shown. (E) 1D profile of the vertical magnetic field component Bz and current density J along a horizontal line crossing perpendicular to the core of the CS (that is, the point with the largest J). Location of the line is denoted by the short lines in (A) and (C). The diamonds denote values on the grid nodes. The thickness of CS is denoted, which is defined by the FWHM of a Gauss function fitting (the thin black curve) of the profile of current density. (F) Horizontal velocity and Alfvénic Mach number along the same line shown in (E). Before the onset of reconnection, the horizontal flow plays a role of thinning the current layer to CS; once the reconnection starts, the inflow Mach number measures the reconnection rate.
Supplementary Video 3
Animation for panels (A) and (B) of Fig. 4.
Supplementary Video 4
Evolution of magnetic field lines during the eruption shown in two different view angles. Also an animation for panel (A) of Fig. 5.
Supplementary Video 5
Comparison of the eruptive structure with that of an observed flare eruption. Left: A GOES X8.2 eruptive flare that occurred on 2017 September 10 as observed by the Atmospheric Imaging Assembly on board the Solar Dynamic Observatory in three EUV emission lines including 131, 211 and 171 Å. Right: The simulated eruption process. The background is shown with the distribution of J/B on the central cross section, and some sampled magnetic field lines are plotted in comparison with the structure of the coronal loops in observation.
Supplementary Video 6
Evolution of 3D structure and different slices of the CS. Also an animation for panel (B) of Fig. 5.
Supplementary Video 7
Evolution of 11 sampled magnetic field lines and their rising speeds in the process of reconnection and join in the MFR. In the left two panels, the three magnetic field lines are plotted in three different colors. The bottom surface is shown with the contour of Bz, and the central cross section, that is, the x = 0 slice, is shown with the J/B and velocity v. In the right panel, the colored curves show the evolution of rising speed at middle of these field lines, that is, the point where the field lines cross the central cross section. The gray curve shows the increasing rate of kinetic energy.
Supplementary Video 8
Structure of the block-based AMR grid. Two cross sections of the grid and current density are shown. The black lines denote the blocks, each of which further consists of 83 cells. Note the strong current regions are always resolved by meshes with the finest grids.
Supplementary Video 9
Comparison of CS evolution and velocity in runs with different highest resolutions.
Supplementary Video 10
Animation for Supplementary Figure 9. The left panel shows magnetic squashing degree Q on central vertical slice (that is, x = 0 plane). The right panels show Q, the magnetic twist number Tw, and current density on the bottom surface.
Rights and permissions
About this article
Cite this article
Jiang, C., Feng, X., Liu, R. et al. A fundamental mechanism of solar eruption initiation. Nat Astron 5, 1126–1138 (2021). https://doi.org/10.1038/s41550-021-01414-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-021-01414-z
This article is cited by
-
Developments of a fundamental mechanism for initiation of solar eruptions
Reviews of Modern Plasma Physics (2024)
-
Complete replacement of magnetic flux in a flux rope during a coronal mass ejection
Nature Astronomy (2023)
-
Properties and Energetics of Magnetic Reconnection: I. Evolution of Flare Ribbons
Solar Physics (2022)
-
The return of the jet
Nature Astronomy (2021)