Abstract
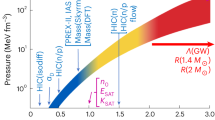
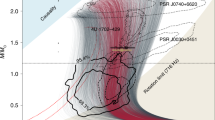
The properties of neutron stars are determined by the nature of the matter that they contain. These properties can be constrained by measurements of the star’s size. We obtain stringent constraints on neutron-star radii by combining multimessenger observations of the binary neutron-star merger GW170817 with nuclear theory that best accounts for density-dependent uncertainties in the equation of state. We construct equations of state constrained by chiral effective field theory and marginalize over these using the gravitational-wave observations. Combining this with the electromagnetic observations of the merger remnant that imply the presence of a short-lived hypermassive neutron star, we find that the radius of a 1.4 M⊙ neutron star is \({R}_{1.4{M}_{\odot }}={11.0}_{-0.6}^{+0.9}\ {\rm{km}}\) (90% credible interval). Using this constraint, we show that neutron stars are unlikely to be disrupted in neutron star–black hole mergers; subsequently, such events will not produce observable electromagnetic emission.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
All data are available in the manuscript or the Supplementary Information. Full posterior data samples are available at https://github.com/sugwg/gw170817-eft-eos. The gravitational-wave data used in this work were obtained from the Gravitational Wave Open Science Center (GWOSC) at https://www.gw-openscience.org.
Code availability
All software used in this analysis is open source and available from https://github.com/gwastro/pycbc.
References
Lattimer, J. M. & Prakash, M. Neutron star structure and the equation of state. Astrophys. J. 550, 426–442 (2001).
Özel, F. & Freire, P. Masses, radii, and the equation of state of neutron stars. Annu. Rev. Astron. Astrophys. 54, 401–440 (2016).
Gendreau, K., Arzoumanian, Z. & Okajima, T. The Neutron star Interior Composition ExploreR (NICER): an explorer mission of opportunity for soft X-ray timing spectroscopy. Proc. SPIE 8443 844313 (2012).
Abbott, B. P. et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017).
Abbott, B. P. et al. Multi-messenger observations of a binary neutron star merger. Astrophys. J. 848, L12 (2017).
De, S. et al. Tidal deformabilities and radii of neutron stars from the observation of GW170817. Phys. Rev. Lett. 121, 091102 (2018); erratum 121, 259902 (2018).
Abbott, B. P. et al. GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121, 161101 (2018).
Abbott, B. P. et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 9, 011001 (2019).
Radice, D. & Dai, L. Multimessenger parameter estimation of GW170817. Eur. Phys. J. A 55, 50 (2019).
Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 251, 288–292 (1990).
Weinberg, S. Effective chiral lagrangians for nucleon–pion interactions and nuclear forces. Nucl. Phys. B 363, 3–18 (1991).
van Kolck, U. Few nucleon forces from chiral lagrangians. Phys. Rev. C 49, 2932–2941 (1994).
Epelbaum, E., Hammer, H. W. & Meissner, U. G. Modern theory of nuclear forces. Rev. Mod. Phys. 81, 1773–1825 (2009).
Machleidt, R. & Entem, D. R. Chiral effective field theory and nuclear forces. Phys. Rep. 503, 1–75 (2011).
Carlson, J. et al. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 87, 1067–1118 (2015).
Tews, I., Margueron, J. & Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 98, 045804 (2018).
Hebeler, K., Lattimer, J. M., Pethick, C. J. & Schwenk, A. Constraints on neutron star radii based on chiral effective field theory interactions. Phys. Rev. Lett. 105, 161102 (2010).
Antoniadis, J. et al. A massive pulsar in a compact relativistic binary. Science 340, 1233232 (2013).
Tews, I., Carlson, J., Gandolfi, S. & Reddy, S. Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophys. J. 860, 149 (2018).
Biwer, C. M. et al. PyCBC inference: a Python-based parameter estimation toolkit for compact binary coalescence signals. Publ. Astron. Soc. Pac. 131, 024503 (2019).
Soares-Santos, M. et al. The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. I. Discovery of the optical counterpart using the dark energy camera. Astrophys. J. 848, L16 (2017).
Cantiello, M. et al. A precise distance to the host galaxy of the binary neutron star merger GW170817 using surface brightness fluctuations. Astrophys. J. 854, L31 (2018).
Margalit, B. & Metzger, B. D. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophys. J. 850, L19 (2017).
Bauswein, A., Just, O., Janka, H. T. & Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. 850, L34 (2017).
Bauswein, A., Baumgarte, T. W. & Janka, H.-T. Prompt merger collapse and the maximum mass of neutron stars. Phys. Rev. Lett. 111, 131101 (2013).
Köppel, S., Bovard, L. & Rezzolla, L. A general-relativistic determination of the threshold mass to prompt collapse in binary neutron star mergers. Astrophys. J. 872, L16 (2019).
Shibata, M., Zhou, E., Kiuchi, K. & Fujibayashi, S. Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. D 100, 023015 (2019).
Cromartie, H. T. et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 4, 72–76 (2020).
Bedaque, P. & Steiner, A. W. Sound velocity bound and neutron stars. Phys. Rev. Lett. 114, 031103 (2015).
Lattimer, J. M. & Prakash, M. in From Nuclei to Stars (ed. Lee, S) 275–304 (UK World Scientific, 2011).
Hannam, M., Brown, D. A., Fairhurst, S., Fryer, C. L. & Harry, I. W. When can gravitational-wave observations distinguish between black holes and neutron stars? Astrophys. J. 766, L14 (2013).
Abbott, B. P. et al. Model comparison from LIGO-Virgo data on GW170817’s binary components and consequences for the merger remnant. Class. Quant. Grav. 37, 045006 (2020).
Advanced LIGO Anticipated Sensitivity Curves LIGO-DCC-T0900288 (LIGO Scientific Collaboration, 2010): https://dcc.ligo.org/LIGO-T0900288/public
Hinderer, T. et al. Distinguishing the nature of comparable-mass neutron star binary systems with multimessenger observations: GW170817 case study. Phys. Rev. D 100, 06321 (2019).
Foucart, F. Black hole–neutron star mergers: disk mass predictions. Phys. Rev. D 86, 124007 (2012).
Bauswein, A., Goriely, S. & Janka, H.-T. Systematics of dynamical mass ejection, nucleosynthesis, and radioactively powered electromagnetic signals from neutron-star mergers. Astrophys. J. 773, 78 (2013).
Hotokezaka, K. et al. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 87, 024001 (2013).
LIGO Scientific Collaboration & the Virgo Collaboration GRB Coordinates Network Circular Service 25333 (2019).
Foucart, F., Hinderer, T. & Nissanke, S. Remnant baryon mass in neutron star–black hole mergers: predictions for binary neutron star mimickers and rapidly spinning black holes. Phys. Rev. D 98, 081501 (2018).
Margalit, B. & Metzger, B. D. The multi-messenger matrix: the future of neutron star merger constraints on the nuclear equation of state. Astrophys. J. 880, L15 (2019).
Wijnands, R., Degenaar, N. & Page, D. Cooling of accretion-heated neutron stars. J. Astrophys. Astron. 38, 49 (2017).
Brown, E. F. & Cumming, A. Mapping crustal heating with the cooling lightcurves of quasi-persistent transients. Astrophys. J. 698, 1020 (2009).
Lewin, W. H. G. & van der Klis, M. Compact Stellar X-ray Sources (Cambridge Univ. Press, 2006).
Barkett, K. et al. Gravitational waveforms for neutron star binaries from binary black hole simulations. Phys. Rev. D 93, 044064 (2016).
Narikawa, T. et al. Reanalysis of the binary neutron star merger GW170817 using numerical-relativity calibrated waveform models. Preprint at https://arxiv.org/abs/1910.08971 (2019).
Abbott, B. P. et al. Prospects for observing and localizing gravitational-wave transients with advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Rel. 21, 3 (2018).
Abbott, B. P. et al. GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and Virgo during the first and second observing runs. Phys. Rev. X 9, 031040 (2019).
Melendez, J. A., Wesolowski, S. & Furnstahl, R. J. Bayesian truncation errors in chiral effective field theory: nucleon-nucleon observables. Phys. Rev. C 96, 024003 (2017).
Lynn, J. E. et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering, and neutron matter. Phys. Rev. Lett. 116, 062501 (2016).
Lonardoni, D. et al. Properties of nuclei up to A = 16 using local chiral interactions. Phys. Rev. Lett. 120, 122502 (2018).
Lynn, J. E., Tews, I., Gandolfi, S. & Lovato, A. Quantum Monte Carlo methods in nuclear physics: recent advances. Annu. Rev. Nucl. Part. Sci. 69, 279–305 (2019).
Tews, I. Spectrum of shear modes in the neutron-star crust: estimating the nuclear-physics uncertainties. Phys. Rev. C 95, 015803 (2017).
Tews, I., Margueron, J. & Reddy, S. Confronting gravitational-wave observations with modern nuclear physics constraints. Eur. Phys. J. A 55, 97 (2019).
Vallisneri, M., Kanner, J., Williams, R., Weinstein, A. & Stephens, B. The LIGO Open Science Center. J. Phys. Conf. Ser. 610, 012021 (2015).
Allen, B., Anderson, W. G., Brady, P. R., Brown, D. A. & Creighton, J. D. E. FINDCHIRP: an algorithm for detection of gravitational waves from inspiraling compact binaries. Phys. Rev. D 85, 122006 (2012).
Foreman-Mackey, D., Hogg, D. W., Lang, D. & Goodman, J. emcee: the MCMC hammer. Publ. Astron. Soc. Pac. 125, 306–312 (2013).
Vousden, W. D., Farr, W. M. & Mandel, I. Dynamic temperature selection for parallel tempering in Markov chain Monte Carlo simulations. Mon. Not. R. Astron. Soc. 455, 1919–1937 (2015).
Speagle, J. S. dynesty: a dynamic nested sampling package for estimating bayesian posteriors and evidences. Preprint at https://arxiv.org/abs/1904.02180 (2019).
Burgay, M. et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 426, 531–533 (2003).
Ade, P. A. R. et al. Planck 2015 results. XIII. cosmological parameters. Astron. Astrophys 594, A13 (2016).
Sathyaprakash, B. S. & Dhurandhar, S. V. Choice of filters for the detection of gravitational waves from coalescing binaries. Phys. Rev. D 44, 3819–3834 (1991).
Buonanno, A., Iyer, B., Ochsner, E., Pan, Y. & Sathyaprakash, B. S. Comparison of post-Newtonian templates for compact binary inspiral signals in gravitational-wave detectors. Phys. Rev. D 80, 084043 (2009).
Mikoczi, B., Vasuth, M. & Gergely, L. A. Self-interaction spin effects in inspiralling compact binaries. Phys. Rev. D 71, 124043 (2005).
Arun, K. G., Buonanno, A., Faye, G. & Ochsner, E. Higher-order spin effects in the amplitude and phase of gravitational waveforms emitted by inspiraling compact binaries: ready-to-use gravitational waveforms. Phys. Rev. D 79, 104023 (2009); erratum 84, 049901 (2011).
Bohé, A., Marsat, S. & Blanchet, L. Next-to-next-to-leading order spin-orbit effects in the gravitational wave flux and orbital phasing of compact binaries. Class. Quant. Grav. 30, 135009 (2013).
Vines, J., Flanagan, E. E. & Hinderer, T. Post-1-Newtonian tidal effects in the gravitational waveform from binary inspirals. Phys. Rev. D 83, 084051 (2011).
Dietrich, T., Bernuzzi, S. & Tichy, W. Closed-form tidal approximants for binary neutron star gravitational waveforms constructed from high-resolution numerical relativity simulations. Phys. Rev. D 96, 121501 (2017).
Dietrich, T. et al. Matter imprints in waveform models for neutron star binaries: tidal and self-spin effects. Phys. Rev. D 99, 024029 (2019).
Husa, S. et al. Frequency-domain gravitational waves from nonprecessing black-hole binaries. I. New numerical waveforms and anatomy of the signal. Phys. Rev. D 93, 044006 (2016).
Khan, S. et al. Frequency-domain gravitational waves from nonprecessing black-hole binaries. II. A phenomenological model for the advanced detector era. Phys. Rev. D 93, 044007 (2016).
Villar, V. A. et al. The combined ultraviolet, optical, and near-infrared light curves of the kilonova associated with the binary neutron star merger GW170817: unified data set, analytic models, and physical implications. Astrophys. J. 851, L21 (2017).
Kiuchi, K., Kyutoku, K., Shibata, M. & Taniguchi, K. Revisiting the lower bound on tidal deformability derived by at 2017gfo. Astrophys. J. 876, L31 (2019).
Bauswein, A. & Stergioulas, N. Semi-analytic derivation of the threshold mass for prompt collapse in binary neutron star mergers. Mon. Not. R. Astron. Soc. 471, 4956–4965 (2017).
Shibata, M. et al. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 96, 123012 (2017).
Rezzolla, L., Most, E. R. & Weih, L. R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. 852, L25 (2018).
Ruiz, M., Shapiro, S. L. & Tsokaros, A. GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass. Phys. Rev. D 97, 021501 (2018).
Lattimer, J. M. & Schramm, D. N. Black-hole–neutron-star collisions. Astrophys. J. 192, L145 (1974).
Shibata, M. & Taniguchi, K. Merger of black hole and neutron star in general relativity: tidal disruption, torus mass, and gravitational waves. Phys. Rev. D 77, 084015 (2008).
Kyutoku, K., Ioka, K., Okawa, H., Shibata, M. & Taniguchi, K. Dynamical mass ejection from black hole–neutron star binaries. Phys. Rev. D 92, 044028 (2015).
Pannarale, F. & Ohme, F. Prospects for joint gravitational-wave and electromagnetic observations of neutron-star–black-hole coalescing binaries. Astrophys. J. 791, L7 (2014).
Barbieri, C., Salafia, O. S., Perego, A., Colpi, M. & Ghirlanda, G. Electromagnetic counterparts of black hole–neutron star mergers: dependence on the neutron star properties. Eur. Phys. J. A 56, 8 (2020).
Bardeen, J. M., Press, W. H. & Teukolsky, S. A. Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 178, 347–370 (1972).
Acknowledgements
We thank B. Allen, W. Kastaun, J. Lattimer and B. Metzger for valuable discussions. This work was supported by US National Science Foundation grants PHY-1430152 to the JINA Center for the Evolution of the Elements (S.R.), PHY-1707954 (D.A.B. and S.D.); US Department of Energy grant DE-FG02-00ER41132 (S.R.); NASA Hubble Fellowship grant number HST-HF2-51412.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555 (B.M.); and the US Department of Energy, Office of Science, Office of Nuclear Physics, under contract DE-AC52-06NA25396, the Los Alamos National Laboratory (LANL) LDRD programme and the NUCLEI SciDAC programme (I.T.). D.A.B., S.D. and B.M. thank the Kavli Institute for Theoretical Physics (KITP) where portions of this work were completed. KITP is supported in part by the National Science Foundation under grant number NSF PHY-1748958. Computational resources have been provided by Los Alamos Open Supercomputing via the Institutional Computing (IC) programme, by the National Energy Research Scientific Computing Center (NERSC), by the Jülich Supercomputing Center, by the ATLAS Cluster at the Albert Einstein Institute in Hannover, and by Syracuse University. GWOSC is a service of LIGO Laboratory, the LIGO Scientific Collaboration and the Virgo Collaboration. LIGO is funded by the National Science Foundation. Virgo is funded by the French Centre National de Recherche Scientifique (CNRS), the Italian Istituto Nazionale della Fisica Nucleare (INFN) and the Dutch Nikhef, with contributions by Polish and Hungarian institutes. B.M. is a NASA Einstein Fellow.
Author information
Authors and Affiliations
Contributions
Conceptualization: D.A.B., C.D.C., B.K., B.M., S.R., I.T. Data curation: D.A.B., C.D.C., S.D., I.T. Formal analysis, C.D.C., S.M.B., I.T., S.D. Funding acquisition: D.A.B., B.K., B.M., S.R., I.T. Methodology: D.A.B., C.D.C., S.D., B.K., B.M., S.R., I.T. Project administration: D.A.B., B.K., S.R., I.T. Resources: D.A.B., B.K., I.T. Software: D.A.B., S.M.B., C.D.C., S.D., S.K., B.M., I.T. Supervision: D.A.B., B.K., S.R. Validation: D.A.B., S.M.B., C.D.C., S.D., I.T. Visualization: S.M.B., C.D.C., B.M. Writing—original draft: D.A.B., S.M.B., C.D.C., I.T. Writing—review and editing: D,.A.B., S.M.B., C.D.C., S.D., B.K., B.M., S.R., I.T.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Capano, C.D., Tews, I., Brown, S.M. et al. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat Astron 4, 625–632 (2020). https://doi.org/10.1038/s41550-020-1014-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-020-1014-6
This article is cited by
-
Determination of the equation of state from nuclear experiments and neutron star observations
Nature Astronomy (2024)
-
Quark stars in the pure pseudo-Wigner phase
Astrophysics and Space Science (2024)
-
Strongly interacting matter exhibits deconfined behavior in massive neutron stars
Nature Communications (2023)
-
Bounding the QCD Equation of State with the Lattice
Journal of High Energy Physics (2023)
-
Studies of the equation-of-state of nuclear matter by heavy-ion collisions at intermediate energy in the multi-messenger era
La Rivista del Nuovo Cimento (2023)