Abstract
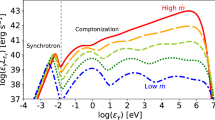
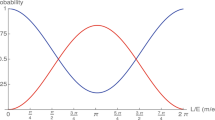
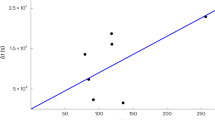
Over the past 15 years there has been considerable interest in the possibility of quantum-gravity-induced in vacuo dispersion, the possibility that spacetime itself might behave essentially like a dispersive medium for particle propagation. Two recent studies have exposed what might be in vacuo dispersion features for gamma-ray-burst (GRB) neutrinos of energy in the range of 100 TeV and for GRB photons with energy in the range of 10 GeV. We here show that these two features are roughly compatible with a description such that the same effects apply over four orders of magnitude in energy. We also show that it should not happen so frequently that such pronounced features arise accidentally, as a result of (still unknown) aspects of the mechanisms producing photons at GRBs or as a result of background neutrinos accidentally fitting the profile of a GRB neutrino affected by in vacuo dispersion.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Amelino-Camelia, G. Quantum-spacetime phenomenology. Living Rev. Rel. 16, 5 (2013).
Jacob, U. & Piran, T. Neutrinos from gamma-ray bursts as a tool to explore quantum-gravity-induced Lorentz violation. Nat. Phys. 3, 87–90 (2007).
Amelino-Camelia, G. & Smolin, L. Prospects for constraining quantum gravity dispersion with near term observations. Phys. Rev. D 80, 084017 (2009).
Amelino-Camelia, G., Ellis, J., Mavromatos, N. E., Nanopoulos D. V. & Sarkar, S. Tests of quantum gravity from observations of gamma-ray bursts. Nature 393, 763–765 (1998).
Gambini R. & Pullin, J. Nonstandard optics from quantum space-time. Phys. Rev. D 59, 124021 (1999).
Alfaro, J., Morales-Tecotl, H. A. & Urrutia, L. F. Quantum gravity corrections to neutrino propagation. Phys. Rev. Lett. 84, 2318–2321 (2000).
Amelino-Camelia, G. & Majid, S. Waves on noncommutative space-time and gamma-ray bursts. Int. J. Mod. Phys. A 15, 4301–4324 (2000).
Myers, R. C. & Pospelov, M. Ultraviolet modifications of dispersion relations in effective field theory. Phys. Rev. Lett. 90, 211601 (2003).
Amelino-Camelia, G., Guetta, D. & Piran, T. IceCube neutrinos and Lorentz invariance violation. Astrophys. J. 806, 269 (2015).
Stecker, F. W., Scully, S. T., Liberati, S. & Mattingly, D. Searching for traces of Planck-scale physics with high energy neutrinos. Phys. Rev. D 91, 045009 (2015).
Waxman, E. & Bahcall, J. N. High energy neutrinos from cosmological gamma-ray burst fireballs. Phys. Rev. Lett. 78, 2292–2295 (1997).
Rachen, J. P. & Meszaros, P. Cosmic rays and neutrinos from gamma-ray bursts. AIP Conf. Proc. 428, 776 (1997).
Guetta, D., Hooper, D., Alvarez-Miniz, J., Halzen F. & Reuveni, E. Neutrinos from individual gamma-ray bursts in the BATSE catalog. Astropart. Phys. 20, 429–455 (2004).
Ahlers, M., Gonzalez-Garcia, M. C. & Halzen, F. GRBs on probation: testing the UHE CR paradigm with IceCube. Astropart. Phys. 35, 87–94 (2011).
Amelino-Camelia, G., Barcaroli, L., D'Amico, G., Loret N. & Rosati, G. IceCube and GRB neutrinos propagating in quantum spacetime. Phys. Lett. B 761, 318–325 (2016).
Amelino-Camelia, G., Barcaroli, L., D'Amico, G., Loret N. & Rosati, G. Quantum-gravity-induced dual lensing and IceCube neutrinos. Int. J. Mod. Phys. D 0, 1750076–1750096 (2017).
Zhang, S. & Ma, B. Q. Lorentz violation from gamma-ray bursts. Astropart. Phys. 61, 108–112 (2014).
Xu, H. & Ma, B. Q. Light speed variation from gamma-ray bursts. Astropart. Phys. 82, 72–76 (2016).
Xu, H. & Ma, B. Q. Light speed variation from gamma ray burst GRB 160509A. Phys. Lett. B 760, 602–604 (2016).
Rosati, G., Amelino-Camelia, G., Marciano, A. & Matassa, M. Planck-scale-modified dispersion relations in FRW spacetime. Phys. Rev. D 92, 124042 (2015).
Ade, P. A. R. et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594, A13 (2016).
Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Rel. 8, 5 (2005).
Szabo, R. J. Quantum field theory on noncommutative spaces. Phys. Rep. 378, 207–299 (2003).
Calmet, X., Hsu, S. D. H. & Reeb, D. Grand unification and enhanced quantum gravitational effects. Phys. Rev. Lett. 101, 171802 (2008).
Robinson, S. P. & Wilczek, F. Gravitational correction to running of gauge couplings. Phys. Rev. Lett. 96, 231601 (2006).
Shao, L. et al. A new measurement of the spectral lag of gamma-ray bursts and its implications for spectral evolution behaviors. Preprint at http://arXiv.org/abs/1610.07191 (2016).
Aartsen, M. G. et al. Evidence for astrophysical muon neutrinos from the northern sky with IceCube. Phys. Rev. Lett. 115, 081102 (2015).
IceCube Collaboration. Energy reconstruction methods in the IceCube neutrino telescope. J. Instrum. 9, P03009 (2014)
Kadler, M. et al. Coincidence of a high-fluence blazar outburst with a PeV-energy neutrino event. Nat. Phys. 12, 807–814 (2016)
Bressieux, J. Testing and Comparison of Muon Energy Estimators for the Icecube Neutrino Observatory. Master’s thesis, Univ. Wisconsin and École Polytechnique Fédérale de Lausanne (2009); http://lphe.epfl.ch/publications/diplomas/jb.master.pdf
IceCube Collaboration. First observation of PeV-energy neutrinos with IceCube. Phys. Rev. Lett. 111, 021103–021110 (2013)
IceCube Collaboration. Evidence for high-energy extraterrestrial neutrinos at the IceCube detector. Science 342, 1242856–1242894 (2013)
IceCube Collaboration. Observation of high-energy astrophysical neutrinos in three years of IceCube data. Phys. Rev. Lett. 113, 101101–101109 (2014)
IceCube Collaboration. Observation of astrophysical neutrinos in four years of IceCube data. Proc. Sci. ICRC2015, 1081–1089 (2015)
Abdo, A. A. et al. A limit on the variation of the speed of light arising from quantum gravity effects. Nature 462, 331–334 (2009).
Vasileiou, V. et al. Constraints on Lorentz invariance violation from Fermi-large area telescope observations of gamma-ray bursts. Phys. Rev. D 87, 122001 (2013).
Aharonian, F. et al. Limits on an energy dependence of the speed of light from a flare of the active galaxy PKS 2155-304. Phys. Rev. Lett. 101, 170402–170407 (2008).
Acknowledgements
We are very grateful to B.-Q. Ma and S. Puccetti for valuable discussions on some of the data used here. We also gratefully acknowledge conversations with F. Fiore and L. Smolin. The work of G.R. was supported by funds provided by the National Science Center under the agreement DEC-2011/02/A/ST2/00294. N.L. acknowledges support by the European Union Seventh Framework Programme (FP7 2007-2013) under grant agreement 291823 Marie Curie FP7-PEOPLE-2011-COFUND (the new International Fellowship Mobility Programme for Experienced Researchers in Croatia — NEWFELPRO), and also partial support from the H2020 Twinning project no. 692194, ‘RBI-TWINNING’.
Author information
Authors and Affiliations
Contributions
G.A.-C. was in charge of project planning, led most of the interpretation, and assisted in data analysis. G.D'A. and G.R. had the leading role in the data analysis and assisted in the interpretation. N.L. assisted in the data analysis and assisted in the interpretation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Table 1 and Supplementary Figure 1. (PDF 119 kb)
Rights and permissions
About this article
Cite this article
Amelino-Camelia, G., D’Amico, G., Rosati, G. et al. In vacuo dispersion features for gamma-ray-burst neutrinos and photons. Nat Astron 1, 0139 (2017). https://doi.org/10.1038/s41550-017-0139
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41550-017-0139
This article is cited by
-
Could quantum gravity slow down neutrinos?
Nature Astronomy (2023)
-
Lorentz and CPT breaking in gamma-ray burst neutrinos from string theory
Journal of High Energy Physics (2023)
-
Lorentz invariance beyond the Planck scale
Nature Physics (2022)
-
Search for quantum gravity using astrophysical neutrino flavour with IceCube
Nature Physics (2022)
-
Implications of SU(2)L gauge invariance for constraints on Lorentz violation
Journal of High Energy Physics (2021)