Abstract
The plant shoot apical meristem holds a stem cell niche from which all aerial organs originate. Using a computational approach we show that a mixture of monomers and heterodimers of the transcription factors WUSCHEL and HAIRY MERISTEM is sufficient to pattern the stem cell niche, and predict that immobile heterodimers form a regulatory “pocket” surrounding the stem cells. The model achieves to reproduce an array of perturbations, including mutants and tissue size modifications. We also show its ability to reproduce the recently observed dynamical shift of the stem cell niche during the development of an axillary meristem. The work integrates recent experimental results to answer the longstanding question of how the asymmetry of expression between the stem cell marker CLAVATA3 and its activator WUSCHEL is achieved, and recent findings of plasticity in the system.
Similar content being viewed by others
Introduction
The shoot apical meristem (SAM) is a dome shaped tissue located at the tip of the shoot. The stem cell niche it harbours is at the origin of all the aerial plant organs, making it a critical regulator of plant development.1 It remains active over the lifespan of the plant, continuously providing new cells for developing organs while maintaining its shape and specific gene-expression domains stable; a feat enabled by a tight homoeostatic control.
This control is largely dependent on the CLAVATA/WUSCHEL (CLV/WUS) negative feedback loop.2 A dialogue between the apex of the SAM—the stem cell domain—and its centre is carried out by the transcription factor WUS and the CLAVATA signalling system. WUS is specifically expressed in a central domain; diffusing, it promotes stem cell fate at the tip of the SAM and represses differentiation at its periphery.3,4,5,6 The CLV3 peptide is expressed in the stem cell domain, and is activated by WUS. It diffuses towards the inner layers of the meristem where, upon binding the CLV1 receptors, it represses the expression of WUS, thereby closing the feedback loop.7,8 The antagonism between WUS and CLAVATA signalling is reflected in their perturbations: wus plants exhibit small or even arrested meristems, while clavata plants have massively enlarged meristems associated with increased organ counts.
The expression of WUS is promoted by cytokinin, making the plant hormone a major factor controlling the SAM homoeostasis.9,10,11,12 The expression domains of the enzymes catalysing the synthesis of the active hormone and its receptors stress the importance of the dichotomy between the external cell layers and the inner tissue of the meristem, which can explain the scaling of the SAM domains with its size.13
The current spatial descriptions of CLV3 regulation, and by extension, of the activation of stem cells, suggest a co-activation by WUS and either an apical14 or epidermal5,6,13,15,16 hypothetical signal, to generate an asymmetry between the stem cell domain and its main activator WUS. When it comes to the CLV3 expression domain, the triple hairy meristem (ham) mutant displays a particularly puzzling phenotype.17 In this mutant, CLV3 is expressed in the centre of the meristem, overlapping with the expression domain of WUS; the apical or epidermal activation of CLV3 seem difficult to conciliate with this observation.
The HAM transcription factors were recently shown to dimerise with WUS, with which they share multiple transcriptional targets. Among the HAMs, HAM1 and HAM2 were also shown to be expressed mostly within the inner tissue of the meristem,18 in a pattern reminiscent of the cytokinin receptors.13
In the following, we explore the hypothesis that the HAM–WUS dimer represses the expression of CLV3 away from the WUS domain, inspired by the reported central expression of CLV3 in the meristem of ham plants. We first show experimentally that the expression pattern of HAM1 and HAM2 scales with the size of the meristem while remaining mainly expressed in the inner tissue layers; a pattern consistent with an epidermal repression of the two genes. We show that an activation of CLV3 by WUS monomers together with a repression by HAM–WUS dimers is sufficient to pattern the stem cell domain while explaining the triple ham mutant, both using a two-dimensional (2D) representation of the meristem and a three-dimensional tissue template generated from confocal microscopy. The resulting model reproduces the asymmetry between WUS and CLV3 expression domains and multiple experimentally described perturbations of the system. It allows for a plastic stem cell domain location and can provide an explanation for this recently observed developmental phenomena.
Results
The expression domains of HAM1 and HAM2 scales with meristem size
The expression domains of HAM1 and HAM2 were described in ref.18 In both cases, the gene expression was markedly stronger in the centre of the meristem than close to the epidermis. Since it is not known what regulates the HAM expression, we introduced perturbations to get an indication of the regulatory motif. To do so, we grew plants in different conditions, such that their SAM size would vary. Whatever the size of the meristematic tissue, the expression of both HAM1 and HAM2 is weak or null close to the epidermis, and relatively stronger in a large central domain in the rib meristem (Fig. 1a, b). Primordia also appear to have a strong influence on the pattern; HAM1 and HAM2 expression are at their strongest where organs emerge.
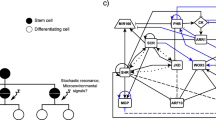
Expression of pHAM1::YPET-N7 a and pHAM2::YPET-N7 b in representative meristems of different sizes. Meristems were obtained by growing plants on soil, on soil supplied with fertiliser, or on a mixture of soil and sand, leading to meristems of various sizes. Top images show z-projections (sum slices) and bottom images show sections through the centre of the inflorescence meristem. YPET signal is represented using the Fire lookup table of ImageJ. Scale bar: 10 μm. c Schematic of the model: the epidermis controls WUS expression with an IFF-like motif (both inducing and repressing its expression), as introduced in Gruel et al.13 The epidermis also represses the expression of HAM. HAM and WUS monomers can heterodimerize; WUS monomer induces the expression of CLV3 while the heterodimer represses it. Finally, the CLV3 peptide represses the expression of WUS. d Parameter optimisations result in three possible behaviours. The panel presents the expression of WUS, CLV3 and HAM on a colour scale varying from blue (no expression) to green (optimisation target expression) to red (twice the target expression). HAM–WUS dimers and WUS monomers are plotted on a relative colour scale varying from blue (minimal concentration) to red (maximal concentration). Additionally the outline of the pocket formed by the HAM–WUS dimers is displayed (smaller meristems), in blue are concentrations below the maximal value found in the epidermis and in red are concentrations above this value
The expression pattern of the two genes scales with the meristem size, while always avoiding the outer layers of the central SAM. This is consistent with a repression of HAM expression by a signal originating in the epidermis, as previously suggested for the cytokinin receptors,13 and this hypothesis for HAM regulation will be further explored in the following.
An epidermis-driven model explains the expression pattern of the stem cell domain
Given the HAM domains spatially overlap with WUS, a WUS–HAM dimer would be expected to have its concentration peak in the WUS domain and would therefore be an excellent candidate to explain the exclusion of CLV3 from wild-type (WT) meristems, as opposed to ham meristems. However, explaining the apical expression of CLV3 with a combination of two factors expressed directly below is less straightforward, and to explore the hypothesis that HAMs together with WUS, via their physical interaction, are able explain the patterning of the stem cell niche in the SAM, we developed a differential equation model for the spatial expression domains.
In the model (Fig. 1c), WUS expression is regulated by two epidermis-originating morphogens, forming a regulation resembling an incoherent feed-forward motif,19 (IFF-like, notably allowing a non-monotonic function of the distance to the L1); cytokinin acts as an activator while a second signal abstracting the repression of cytokinin receptors from the L1 acts as an inhibitor.13 As suggested by the scaling of HAM1 and HAM2 with the SAM size (Fig. 1a, b), a third epidermis-originating signal represses the expression of HAMs and HAMs, due to their functional redundancy,17 are considered as a single entity. WUS monomers can dimerise with HAM monomers, proteins undergo passive diffusion-like transport (between cells) in the tissue.5,20 Finally, WUS monomers activate the expression of CLV3 while WUS–HAM heterodimers repress the expression, and CLV3 peptides can move in the tissue and repress the expression of WUS.
The model describes the RNA concentration variations of WUS (W), CLV3 (C) and HAM1/HAM2 (H), their corresponding proteins and peptides (WUS monomers (w), CLV3 (c), HAM1/HAM2 monomers (h), HAM–WUS dimers (d)) and the three positional signals produced by the epidermis (cytokinin (Lc), the Arabidopsis histidine kinase (AHK) repressor (La), the HAM repressor (LH)). L and S define the epidermal and meristem–stem boundaries, respectively. Gene expression is described with either Hill functions or Shea–Ackers formalism,21 molecular transport between cells is passive, diffusion-like, and other reactions follow mass action. Each cell of the meristematic representation is described by the following system of ten equations:
A more detailed model description and the model parameter definitions are provided in Materials and methods.
The SAM geometry is described as a half disk, the curved part of its perimeter representing the epidermis and its flat part the connection with the plant stem. This representation allows for simple deformations to mimic SAM size and shape dynamics upon mutations or growth condition variations (Figure S1). Model parameters are optimised to reproduce manually defined domains approximating experimental expression for WUS, HAM and CLV3 at equilibrium (Materials and methods, Figure S2).
Notably, the model achieves to reproduce the expression domains of WUS, HAM and CLV3, and multiple successful parameter values are found with the heuristic optimisation procedure (Fig. 1d—note that the expression domains of HAM1 and HAM2 are represented by a single homogeneous domain covering the inner part of the meristem). Three broadly different behaviours were identified in the resulting parameter sets (Figure S3). In two of them, the HAM–WUS heterodimers organise in a pocket surrounding the stem cell niche (miniature meristems in Fig. 1d). One case shows WUS monomer concentration peaking in the WUS expression domain, the expression domain of CLV3 is in this case thus mostly delimitated by the repressing HAM–WUS heterodimers; this behaviour will be referred to as “pocket repressor” in the following. The second behaviour displaying a pocket of heterodimers sees WUS monomer concentration peaking in the stem cell domain, directly activating CLV3 and the WUS activation plays a prominent role in delineating the CLV3 domain; this behaviour is named “pocket activator”. Finally, the last scenario results in the concentration of all actors of the system peaking along the central vertical axis of the meristem and will be referred to as “central axis”. Similarly to “pocket activator”, this last case sees WUS monomers peaking in the CLV3 domain. The three categories are displayed according to their categorisation rules in Figure S3 and on a planar projection of the parameter space in Figure S4.
As all three alternative behaviours can explain the WT gene-expression domains in the SAM, further analysis is required to assess their biological relevance.
The behaviour of the system hinges on protein differential mobility
First, we analysed the differences between the defined solutions in terms of predicted protein monomer and dimer mobilities. At equilibrium, the shape of the gradient formed by a diffusing molecule is controlled by the ratio between its diffusion rate and consumption rate, this ratio is in the following referred to as mobility. As described in ref.13, the epidermis-originating morphogens with a ratio favouring diffusion form a shallow gradient (i.e., cytokinin and acting at long range), while those favouring degradation fall sharply (i.e., the short-range AHK repressor). Together these signals form the IFF-like regulation of WUS generating the adaptive scaling of the expression domain to the size of the meristem.
In the model, WUS and HAM monomers influence the mobility of each other. Indeed, if a WUS monomer is in the presence of sufficient HAM monomers, rather than diffusing, it will likely be recruited to form a dimer. This also applies to HAM monomers in the presence of a large amount of WUS monomers. As the WUS and HAM expression domains are different, the mobility of the monomers is influenced by their location within the meristem. HAM–WUS heterodimers are consumed by degradation and dissociation. The efficiency of those two reactions is not influenced by secondary species, nor is their diffusion rate; the moblility of the dimers does not vary across the tissue.
We analysed the mobility of the two monomers and the dimer across the central axis of the SAM (Fig. 2). For each of the three categories, and as expected, WUS monomers are more mobile close to the apex of the tissue, where relatively little HAM is found, compared to close to the stem, where HAM is expressed. The opposite holds true for HAM monomers for all three categories as HAM monomers are more mobile close to the stem than they are at the apex. However, the three categories can be differentiated when monomer mobility is compared to dimer dynamics. In the “central axis” category, dimers are the most mobile of the three species. For the “pocket repressor” category, dimers are the least mobile species. For the “pocket activator” category, the dimer mobility is between the maximum and minimum mobility of both dimers.
The dimer mobility is computed following \(\frac{D}{{g + b}}\) and monomer mobility following \(\frac{D}{{g + f[P]}}\) with D the diffusion rate of the considered molecule, g its degradation rate, b dimers dissociation rate, f dimers formation rate and [P] the concentration of the monomeric partner of the considered monomer. For all three panels, the y-axis is the mobility on a logarithmic scale, the x-axis is the central axis of the meristem, with the stem to the left and the apex to the right. For each considered molecule (WUS: red, HAM: green and HAM–WUS: blue), and each position, the mobility value is presented as a boxplot encompassing all optimised parameters belonging to one of the three parameter set categories (the boxes mark the upper and lower quartiles of the data and the line the median, the whiskers extend to 1.5× interquartile range)
It has been suggested that WUS moves between cells via the plasmodesmata, and that the size (e.g., number of green fluorescent connected to WUS) can be restrictive for the mobility.5,20 Given this, the fast moving dimers observed in the “central axis” category would be a less likely scenario.
Perturbations expose behavioural differences between model categories
Next, we explored various perturbations of the system to expose possible variations in the response of the three different categories. In particular we implemented models representing clv, ham and pCLV3::WUS mutants along with changes of the tissue size. These perturbations are selected for having interesting changes to CLV3 and WUS expression domains and characteristic changes in meristem size and shape (Fig. 3).
Each panel plots either the expression of WUS or CLV3 in various scenarios (wild type, clavata, ham, pCLV3::WUS and large meristem) using an example parameter set from the “pocket repressor” category and where parameters have been adjusted to represent the mutants (Materials and methods). The colour map for wild type, clavata and large meristems is the same, varying from blue (no expression) to red (twice the wild-type target expression for optimisations (green) and any value above). The colour map in the ham and pCLV3::WUS scenarios varies between blue and red (minimum and maximum gene expression in the considered settings)
A prerequisite for any model aiming at describing the stem cell dynamics of the SAM is the ability to reproduce the clavata mutants. Abolishing the feedback between CLV3 and WUS yields fasciated meristems showing a reorganisation of gene-expression domains; CLV3 and WUS are expressed in two band like domains spanning the entirety of the upper cell layers of the expanded tissue13,22 (with CLV3 expression in the three to four first cell layers and WUS expression from the third cell layer, the genes notably overlap in the third cell layer).
To investigate the mutant behaviour across parameter values for the three categories, the expression of CLV3 and WUS in WT and in a clavata fasciated meristem was analysed along the central axis (Fig. 4). Little differentiates the three categories, and all display an increase of the expression of both genes. If analysed in more detail, the spatial overlap of the two gene-expression domains is, however, generally larger in the “central axis” and “pocket activator” categories (high CLV3 expression through more than half the WUS domain) than it is for “pocket repressor”, where the latter category presents on average a behaviour closer to observations.13
Model behaviour for the three categories (pocket repressor, pocket activator and central axis—from left to right) and different perturbations (clavata, ham, pCLV3::WUS and large meristem—from top to bottom). In all panels, the activity of CLV3 and WUS promoters is plotted along the central axis of the meristem with the stem to the left and the apex (L1) to the right. For the wild type and clavata meristems, the median, first and last quartile of the absolute expression in a category is plotted. For the three other categories, the relative expression along the axis is plotted. For each perturbation, miniature meristems show the difference between wild-type meristems and perturbation meristems (C—clavata, P—pCLV3::WUS and L—large meristem; the wild-type meristem is used for the ham perturbation.)
The triple ham mutant phenotype, where CLV3 and WUS expression overlap in a central domain,17 is another critical feature for the model to achieve. We analysed the relative expression of CLV3 and WUS along the central axis of the meristem in simulations where the expression of HAM is null (Fig. 4). All three model categories have parameter values from the optimisation that can achieve a central expression of CLV3. Within each category, however, the domain is more or less broad and in some cases the domain even encompasses the whole tissue. The expression of WUS, activated by its epidermal IFF-like motif, is always expressed in a central domain. Due to the overlapping expression of CLV3, repression increases and WUS is consistently less expressed compared to WT. Existing data does not suggest a massive drop of WUS expression in ham mutants, suggesting that either the mutation affects components of the system not modelled in this study (such as CLV3 receptors) or that the CLV3 effect on WUS expression is somehow buffered, as previously suggested.23
A third mutant with an interesting and non-trivial phenotype is the pCLV3::WUS described in ref.24. Plants in which WUS expression is driven by CLV3 promoter exhibit a massively enlarged meristem in which both CLV3 and WUS are expressed in the three outermost cell layers of the tissue. While the direct activation of CLV3 by an hypothetical L1 originating morphogen provides a straightforward way of achieving this behaviour,6,13 it is not obviously the case when WUS and HAM interactions control the activity of the CLV3 promoter. The characteristic expression domains of CLV3 and WUS in this mutant can also be displayed along the central axis (Fig. 4). Notably, a large proportion of the “pocket repressor” models achieve a correct representation of the experimental data, yet many of them fail the test and result in a situation where both genes are expressed at high levels across the whole tissue. The two other categories display such flat expression behaviour in a majority of the parameter values, and when they achieve an expression constrained to the outer cell layers, they do encompass more layers compared to what is seen in experimental data. Once again, the “pocket repressor” models fit data more closely than the other categories.
Finally, we tested the resilience of the WT models to an increase of the tissue size (Fig. 4). “Pocket repressor” models behave more closely to what is seen in experiments in this situation,13 where a large majority of them maintain correct expression patterns (central WUS domain surmounted by an apical CLV3 domain). In the two other categories the spatial segregation of the expression domains often breaks down, and results in a centrally expressed CLV3 domain.
The various mutants explored show a variety a behaviours for each of the categories, with the “pocket repressor” category generally achieving the best results. In order to assess the ability of a single subset of parameters to correctly describe all tested behaviours, we singled out the parameter sets best describing the pCLV3::WUS mutant (Fig. 5, designated as “pocket repressor +”, see Materials and methods). When the “pocket repressor +” parameter sets were tested against the other mutants, they also proved more successful than the rest of the category (“pocket repressor −”). We further explored the mobility of the monomers and dimers for these two categories (Fig. 5). The “pocket repressor +” parameter sets are the parameter sets exhibiting the traits separating the three original categories to the strongest extent; the dimers are the least mobile and display a large mobility differential with the monomers.
In the top row and following the conventions of Fig. 4, the parameter sets achieving the best description of the pCLV3::WUS mutant are selected and coloured (pocket repressor+), leaving the rest in grey (pocket repressor −). The two sub-categories are mapped on the other two perturbations, following the same colour scheme. The two bottom panels present the mobility of WUS, HAM and HAM–WUS for the pocket repressor + and pocket repressor − categories, following the conventions of Fig. 3
The position of CLV3 shifts as HAM concentration varies
Recent studies have stressed the dynamics of CLV3 expression, providing interesting test cases for the HAM-based model. Notably, during the development of axillary meristems in the leaf axils, a WUS domain is established centrally in the tissue followed by an overlapping CLV3 domain. As the meristem matures, the CLV3 domain gradually shifts from its central position to the tip of the organ.25 The WUS–HAM model can reproduce this shifting behaviour of CLV3 expression by manipulating HAM production (Fig. 6a). This suggests that during the development of axillary meristem the WUS and CLV3 domains are first established, followed by a gradual expression of HAM proteins. As the HAMs reach their normal expression, the CLV3 domain shifts from the centre of the organ to its tip.
a CLV3 domain shift. For the example parameter set, the production of the HAM genes varies from 0 to 1, the factor is indicated along each panel. The colour scale for CLV3 expression varies from blue (null) to dark red (twice the wild-type expression and above). b Example behaviour of a parameter set optimised on a realistic template. The gene-expression colour map for genes is blue for no expression, green for optimisation target expression, red for twice the target expression and any value above. The colour map for the monomers varies from blue (minimal concentration) to red (maximal concentration). In order to facilitate the visualisation of the pocket formed by the dimer, any value above the maximum dimer concentration in the L1 is displayed with red; blue indicates a low concentration
This observation also relates to recent observations made in plants with an altered CLV3 promoter. As WUS binding sites are deleted, the expression of CLV3 can be shifted to different locations between the apex and the the centre of the meristem.26 The authors discuss multiple hypothesis to explain the phenomenon, involving either WUS and WUS homodimers and/or possibly the involvement of the HAM proteins. Using an optimisation approach similar to the one described for the WUS–HAM model (Materials and methods), we were not able to achieve a correct patterning of CLV3 in models exclusively using WUS monomers and homodimers when the number of dimensions of the geometrical template is higher than one (Figure S5). This leads us to favour the HAM–WUS hypothesis, compared to a WUS–WUS hypothesis as the main regulator of CLV3 expression patterning.
The model is able to describe gene-expression patterns on a realistic 3D meristem geometry
To confirm that a 3D geometry or meristem-specific cell neighbourhood topology does not affect the ability of the model to explain the SAM patterning, we applied the developed optimisation strategy to a 3D cell-segmented meristematic tissue13 (Materials and methods). The description comprises cell volumes and cell contact surfaces for a meristem and early flower primordia. Optimisations resulted in models that successfully describe the gene expression of WUS, HAM and CLV3 (Fig. 6b), confirming that the regulatory network in the model is sufficient to generate the SAM patterns. The size of the tissue makes optimisations more difficult and prevents collecting enough parameter sets for a rigorous exploration of the parameter value space. Still, all seven obtained parameter sets belonged to category “pocket repressor”. While this analysis does not refute that it is possible to find parameter sets of the other categories, this is an indication that the “pocket repressor” category might be the best descriptor of existing data.
Discussion
In this work, we show that two genes (WUS and HAM) expressed within the inner layers of the meristematic tissue are sufficient to pattern the apical stem cell niche of Arabidopsis thaliana. Contrary to previous studies hypothesising a direct regulation of CLV3 by either apical or epidermal signals, the model, based on recent experimental data, achieves the plasticity required to explain the WT and non-apical expression of CLV3 observed in multiple cases: ham,17 mutations of CLV3 promoter,26 lateral buds.25 This plasticity is achieved through the double negative feedback, where the epidermis represses HAM, itself repressing CLV3 together with WUS, and the adaptive scaling of the HAM expression domain itself to meristem size was confirmed in experiments where plants were grown under various nutrient conditions.
Due to the scarcity of available experimental data, we chose an exploratory strategy allowing, not only to test the potential of the model to describe the stem cell niche, but also to explore various ways of doing so. Out of three identified categories, one exhibits a more biologically probable behaviour. In the “pocket repressor” category, where the HAM–WUS dimer forms a pocket repressing the expression of CLV3 both WUS and HAM monomers are more mobile than the dimer they form. In the “pocket repressor +” sub-category, where this diverging behaviour is even more pronounced, the model successfully represents a host of perturbations of the system, including mutants and tissue size modifications; the other categories fail to consistently achieve such results.
The main feature of the category of models able to reproduce experimental data are the repressing pocket formed by the heterodimer of WUS and HAM. While the protein mobility fits well with data on WUS, which have been shown to move between cells via plasmodesmata and where this movement is necessary for correct meristem regulation,5,20 this has yet to be confirmed for HAM proteins. Immobile HAM proteins would require a different expression pattern, closer to the repressing pocket, presently achieved via protein mobility.
Similarly, while WUS and HAM have been shown to have shared transcriptional targets,18 an alternative might be that HAM regulation comes solely from depleting part of the meristem from WUS monomers and hence indirectly inactivating CLV3 expression. This can lead to a similar equilibrium regulation of CLV3 expression, but would more closely resemble the situation of the “pocket activator” than the “pocket repressor” category of solutions, and hence direct repression by the dimer is predicted by the model. Combining the “pocket repressor” category with inactivation by WUS depletion would require the intervention of additional species to repress CLV3 from the centre of the meristem, such as WUS–WUS homodimers. This would however affect the ability of the model to reproduce ham mutants, where CLV3 is expressed where the concentration of all forms of WUS would be highest.
Finally, in this model and as in ref.13, the main spatial readouts regulating the expression profile of cells are various signals originating in the epidermis (such as the long-range diffusing cytokinin or the short-range signals repressing cytokinin activity and HAM expression). As such, modifications of the geometry of the meristematic tissue are directly translated into modifications of the gene-expression domains, possibly explaining how the meristem can adapt the size of its stem cell niche to the size of the host tissue. The handling of HAM in the model additionally allows it to exhibit a plastic positioning of the stem cell niche, and hence to predict recent experiments displaying such plasticity.17,25,26
Materials and methods
Plant material and imaging conditions
The pHAM1::YPET-N7 and pHAM2::YPET-N7 reporter lines (Ler background) have been described previously.18 Plants were grown on soil (Levington F2), on a mixture of half soil and half sand, and watered with or without 1/1/1 fertiliser (Vitafeed Standard) and placed in a constant light room (24 h light, 22 °C, intensity: 160 μmol m−2 s−1) until bolting stage. Imaging was performed as follows: the main inflorescence meristem was cut, dissected under a binocular stereoscopic microscope to remove all the flowers down to stage 3 (as defined in ref.27) and transferred to a box containing an apex culture medium as described in ref.28 Meristems were imaged in water using a 20× long-distance water objective mounted on a LSM780 confocal microscope (Zeiss, Germany). Z-stacks of 2 μm spacing were taken. Z-projections (Sum slices) and orthogonal sections were performed using the ImageJ software (https://fiji.sc/).
The plant count for every conditions was:
pHAM1::YPET-N7:
-
Soil: 17 plants
-
Soil + fertiliser: 11 plants
-
Soil + sand: 20 plants
pHAM2::YPET-N7:
-
Soil: 16 plants
-
Soil + fertiliser: 12 plants
-
Soil + sand: 16 plants
Computational methods
The following describes the differential equations defining the model, the structure used to represent the meristem as well as the methods used to find the equilibrium of the system of differential equations and to optimise model parameters. Methods for the latter are in large following previous work.13 The section first focuses on the methodology developed to optimise the 2D HAM–WUS model, then we present the modifications to that methodology implemented to test the WUS–WUS model and to optimise the HAM–WUS model on the segmented meristematic tissue.
2D meristem geometry and topology
A grid is used to represent the meristem (Figure S1). Centred on the bottom left corner of the grid, a quarter of a circle is drawn; if the centre of a grid cell is located within the circle the cell will belong to the meristem representation.
The boundaries of the meristem representation are straightforwardly extracted from this representation:
-
Cells at the bottom of the grid belong to the sink, connecting the meristem to the stem of the plant (this boundary is discussed in the section: lower boundary condition).
-
Cells on the left row of the grid are at located in the centre of the meristem representation. This boundary is implemented as symmetric, allowing the computations to be limited to half the meristem representation.
-
Cells located on the edge of the circle are the cells of the epidermis.
For a total number of cells belonging to the meristem, n, the sink S and the epidermis L are exported as size n arrays in which each cell is given a value of 1 if belonging to the said boundary and 0 if not. Similarly, each variable of the model is stored as an array of size n.
The neighbourhood N is exported as a n × n matrix where Nij = 1 if cells i and j are neighbours and Nij = 0 if not. The diagonal Nii records the amount of neighbours of i; cells belonging to the symmetric boundary have an additional neighbour representing their connection with the abstracted other half of the meristem.
The tissue template includes 732 cells, the entire model thus counts 7320 equations (10 equations × 732 cells).
Gene expression
WUS and HAM RNA production is modelled with Hill functions. For a set of NA activators Aa and NI inhibitors Ib, the concentration of a RNA X varies as
with V, the maximal rate of RNA production. The Hill constants k set the required concentration of activators or inhibitors to switch a gene between its active and inactive states. The Hill coefficients n control the slope of the transition between states. gX is the degradation rate of the RNA. The equilibrium of X is given by
The production of CLV3 RNA, C, is modelled following Shea–Ackers dynamics,21 describing the binding dynamics of transcription factors on a promoter. Considering a single binding site able to bind either WUS monomers, w, as activators or WUS–HAM dimers, d, as a inhibitors, the regulation is given by
with VC the maximal rate of transcription, kw and kd the association constants for the WUS monomer and the WUS–HAM dimer. gC is the degradation rate of the RNA. The equilibrium concentration of CLV3 RNA is given by
Molecular transport
Molecular movement between cells is modelled by a passive diffusion-like transport. Such diffusing molecules are produced by a gene-expression domain (WUS, CLV3 and HAM) or the L1. This domain is referred to as P, a vector of cell RNA concentrations for gene expression or a vector of 1 or 0 indicating that a cell belongs to the L1 or not. The domain is associated to a production rate px for molecule species x.
The bottom cell layer of the tissue represents the sink, S. As for the L1, it is a vector of 1 and 0. In those cells, diffusing molecules undergo degradation equal to their diffusion rate Dx, approximating a continued flux into the non-modelled tissue below the meristem. Diffusing molecules also undergo a passive degradation of rate gx.
For a vector of concentration of a diffusing molecule x, we have
where Δ is the Laplace operator; transport in the model is assumed to be passive.
For a cell i with ni neighbours j, the diffusion of x follows the discretised version
The equilibrium state of the considered molecule is found by solving
This is done with the sparse.linalg.spsolve function of the SciPy Python package.
Parameter values
We used binarized expression domains derived from the confocal microscopy data as target expression domains (Figure S2). We do not expect the model to perfectly reproduce these domains, and as such we are interested in finding sets of parameter values that reasonably well reproduce the patterns. We do not trying to obtain a single globally optimal set of parameter values, but rather explore the model behaviour for a sub-space of parameter values able to reproduce the expression patterns. In practice, we ran a parameter optimisation algorithm multiple times and extracted multiple parameter sets, and in the following each of these are referred to as “optimised parameters”. Similarly, we use “optimised domains” to refer to expression domains resulting from a model parameterised with an optimised parameter set.
A multi-step model-specific optimisation strategy was designed to infer the parameter values of the model. The main difference with the strategy presented in ref. 13 is the dimerisation of HAM and WUS that introduces additional non-linearities in the model; this step is solved with the Newton’s method.
The strategy, detailed afterwards, can be summed up as follows:
-
1.
WUS domain is optimised for an induced clavata phenotype.
-
2.
WUS domain is optimised for a WT phenotype.
-
3.
CLV3 and HAM domains are optimised for a WT phenotype.
-
4.
CLV3 and HAM domains are optimised for WT and CLV3 is optimised for clavata and ham phenotypes.
-
5.
CLV3 peptide is optimised to match step 2.
-
6.
The equilibrium of the whole system is computed for wild type and clavata and ham phenotypes.
All optimisations are carried out with the L-BFGS algorithm from the SciPy Python package, the parameter values are bounded by [10−8:108]. After each step described above, the subset of optimised parameters (see below) are kept as fixed values in the following steps. The optimisations resulted in 658 acceptable parameter sets for 1600 runs of the optimisation procedure, which ran over a few days on a standard PC. All optimisations started with parameters randomly distributed over [10−2:102].
In the following, diff(P) will refer to computing the equilibrium concentration of a diffusing molecule across the tissue, given a production domain P. P is a cell vector containing either ones (L1) or zeros (non-L1) if the production domain is the L1. P is a cell vector of RNA concentrations if it refers to the expression domains of WUS, CLV3 or HAM1/HAM2 (the equilibrium computation is described in the Molecular transport section). Similarly, \(eq([A_1, \ldots ,A_{N_A}],[I_1, \ldots ,I_{N_I}])\) will refer to computing the equilibrium of a gene expression regulated by NA activators A and NI inhibitors I (both activators and inhibitors are cell vectors of diffusing molecule concentrations; the equilibrium computation is described in the Gene expression section); note that WUS and HAM are computed with Hill functions while CLV3 uses Shea–Ackers.
Target expression domains for WUS, CLV3 and HAM1/HAM2 were manually defined on the optimisation template (Wt, Ct and Ht—Figure S2). They are cell vectors containing ones (cells expressing the considered gene) or zeros (cells not expressing the gene).
(1) WUS expression domain
The first step optimises the WUS domain for a clavata phenotype; the only regulators of WUS here are cytokinin and the AHK repressor, both modelled as morphogens produced in the L1.
The equilibrium for the WUS (W1) domain is computed following:
The cost function minimises the difference between the equilibrium WUS domain and an increased target WUS domain (Wt × 1.5):
where the values for W1 and Wt are from the individual cells i. Parameters \(k_{L_c}\), \(k_{L_a}\), pc, Dc, gc, pa, Da and ga are optimised. As CLV3 is not considered in this step, the equation describing WUS dynamics is reduced to \(\frac{{d[W]}}{{dt}} = V_W \times \frac{{[L_c]^{n_{L_cW}}}}{{k_{L_cW}^{n_{L_cW}} + [L_c]^{n_{L_cW}}}} \times \frac{{k_{L_aW}^{n_{L_aW}}}}{{k_{L_aW}^{n_{L_aW}} + [L_a]^{n_{L_aW}}}} - g_W[W]\). Parameters with fixed value are VW = 4, \(n_{L_c} = 8\) and \(n_{L_a} = 4\).
(2) WUS expression domain
The second step adds CLV3’s effect on WUS; the peptide is produced by the CLV3 target domain. The optimisation minimises the difference between the WUS domain and the WUS target domain. The equilibrium of the WT WUS domain is given by
and the cost function is
Parameters kc, pc and Dc are optimised, and nc = 2 and gc = 1 are kept constant (together with parameters optimised in step 1).
(3) CLV3 and HAM expression domains
This step minimises the difference between CLV3 and HAM1/HAM2 domains and their target domains Ct and Ht. After W and H equilibria are obtained, the equilibrium for the non-linear w, h, d sub-system can be computed using the Newton’s method leading to the equilibrium for C.
With F(x,W,H) the 3i length system containing Eqs. (4)–(6) for all cells, J(x,W,H) its (3i)2 Jacobian matrix and N(F(x,W,H),J(x,W,H)) the Newton’s method applied to find the root of the three-equation system, the equilibrium of CLV3 and HAM is obtained as follows:
The cost function to minimise is given by
Optimised parameters are: \(k_{L_H}\), \(p_{L_H}\), \(D_{L_H}\), pw, Dw, ph, Dh, f, Dd, VC, kw, kd, gh, gw, gd and b. Fixed parameters are VH = 1 and \(n_{L_H} = 4\). The weight ω = 0.08 was chosen after visually observing the effect of various balancing of the components of the cost function over the course of multiple test optimisations.
(4) CLV3 and HAM expression domains
This step uses the previously optimised parameter values as an initial guess to start a second broader optimisation. Here, CLV3 and HAM domains are optimised for WT and CLV3 is optimised for clavata and ham phenotypes.
With Cc and Ch the equilibria of CLV3 in clavata and ham phenotypes, the equilibria for the different genes and conditions are computed by the following procedure:
The cost function is given by:
with weights ω1 = 0.04 and ω2 = 0.2. Parameters \(k_{L_H}\), \(p_{L_H}\), \(D_{L_H}\), pw, Dw, ph, Dh, f, Dd, VC, kw, kd, gh, gw, gd and b are re-optimised.
(5) CLV3 peptide gradient
In this step, the CLV3 peptide gradient produced by the CLV3 domain optimised in the previous step is fitted to the gradient obtained in step 2, and produced by the target CLV3 domain.
C at equilibrium is computed following:
The cost function is given by
Parameters pc, Dc and gc are optimised.
(6) Equilibrium of the complete model
In the final step, the previously optimised sub-parts of the model are assembled and the equilibrium of the full model is computed. The following algorithm is used. It progressively introduces the feedback loop to the clavata mutant to find the global equilibrium of the system.
Lc = diff(L)// cytokinin equilibrium |
La = diff(L)// AHK repressor equilibrium |
LH = diff(L)// HAM repressor equilibrium |
W0 = eq([Lc], [La])// initial WUS (no CLV3 repression) |
H = eq([], [LH])// HAM equilibrium |
w0, h0, d0 = N(F(x, W0, H), J(x, W0, H))// monomer/dimer equilibrium |
D = max_float// sum of the derivatives at current step |
δ = 0.1// step size |
while D > 10−10 do |
C0 = eq([w0], [d0])// initial CLV3 |
c = diff(C0) |
W = eq([Lc][La, c]) × δ + W0 × (1 − δ) // moving WUS slowly towards equilibrium |
w, h, d = N(F(x, W, H), J(x, W, H)) |
C = eq([w][d])// new CLV3 |
if \(\mathop {\sum}\nolimits_i {(C_0 - C)} > 0\) then |
W0 = W; w0 = w; d0 = d// new initial conditions |
else |
δ = δ × 0.1// system below equilibrium, step size decrease |
end |
\(D = \mathop {\sum}\nolimits_i {\frac{{dw}}{{dt}}} + \mathop {\sum}\nolimits_i {\frac{{dh}}{{dt}}} + \mathop {\sum}\nolimits_i {\frac{{dd}}{{dt}}} + \mathop {\sum}\nolimits_i {\frac{{dc}}{{dt}}}\)// new derivatives for stopping criteria |
end |
After multiple optimisation runs, the parameters kept for further analysis are those where \(\mathop {\sum}\nolimits_i {(C - C_t)^2} < 15\) when the system is in equilibrium.
Parameter sets categorisation
Parameter sets are categorised based on the layout of monomers and dimers obtained at the equilibrium of the model.
In the following, we consider the 2D coordinate system with the origin at the centre of the lower boundary. In this system, the apex of the meristem has coordinates (0,30) and the rightmost point belonging to the tissue has coordinates (30,0).
A pocket of dimers is observed if the concentration peak of dimers in the epidermis is not observed at the apex of the meristem. Following this, we categorised as “central axis” the parameter sets displaying an epidermal peak of monomers at the apex of the meristem.
In order to differentiate the rest of the parameter sets, we explored the position of the concentration maximum of WUS monomers along the central axis of the meristem (y-axis). Parameter sets having their maximum in the pocket (y ≥ 21) belong to “pocket activator”, and parameter sets having their maximum outside the pocket (y ≤ 17) belong to “pocket repressor”.
Optimised parameter sets are displayed in Figure S3 according to these categorisation rules. They are also displayed in Figure S4 according to a linear discriminant analysis where the base 10 logarithm of parameter values were centred and scaled before running the linear discriminant analysis from the scikit-learn python package.
The pCLV3::WUS mutants display a enlarged meristem where both WUS and CLV3 exhibit a relatively strong expression in the outer layers of the tissue.24
In order to select the parameter sets displaying a behaviour matching the experimental data as “pocket repressor +”, we retained the parameters presenting a low expression of the two genes in the centre of the meristem. To create a selection criteria, we first normalised the expression values of WUS and CLV3 between 0 and 1 (the maxima are always found in the L1 for this mutant). In the large pCLV3::WUS meristems, where the apex cell has coordinates (0,45), “pocket repressor +” parameter sets have normalised WUS below 0.5 in cells (0,20) and (0,30), and normalised CLV3 below 0.5 in cell (0,30).
WUS–WUS model
In order to test a model in which the combination of WUS monomers and WUS–WUS homodimers would regulate the expression of CLV3, we used the same core model as previously described.
We removed the equations referring to HAM transcription and HAM monomer (Eqs. (2) and (5)). Eq. (6), describing the dimer dynamics, was modified to
and Eq. (4), describing WUS monomer dynamics, was modified to
Finally, the components of the optimisation procedure related to HAM expression were left out. Example results obtained with this approach are presented in Figure S5.
Realistic template
The main difference for the 3D template compared to the 2D template is the use of cell volumes and cell contact surfaces as obtained from the segmentation of the confocal imaging of a meristem tissue.13 The equation controlling the molecular transport of x becomes:
for a cell i with ni neighbours j, with Vi the volume of cell i and Cij the contact surface between cells i and j. Hill coefficients from the optimisations in ref.13 were kept: \(n_{L_cW} = 7.25968619416\), \(n_{L_aW} = 1.99109438845\), nc = 6.66419523049 and in addition nlH = 6 was fixed. Other parameter values were found by the same optimisation strategy as used for the 2D templates.
Lower boundary condition
In the model, we chose to describe the bottom boundary of the meristem template as a sink, abstracting the larger tissues below the meristem along with the forming vasculature (as previously used in ref.13). The boundary removes molecules from the system based on their diffusion rate, effectively affecting molecules with a high diffusion coefficient the most.
We analysed the gradient of the epidermal morphogens controlling the expression of WUS (cytokinin and AHK repressor) for all optimised parameter sets (Figure S6). While cytokinin falls sharply almost to a null value at the boundary, AHK repressor reaches a quasi null value much closer to its production site; cytokinin having a high mobility is highly affected by the boundary while AHK repressor is virtually not affected. Note, the cytokinin gradient is particularly sharp because the optimisation algorithm is minimising the difference between the WUS binary template, and the domain obtained from the Hill functions describing WUS in the model. As the Hill coefficients are fixed, the most efficient way to bring WUS closer to its binary template value is to have a steep cytokinin gradient, where the sink has an important impact.
The Hill function describing the WUS domain can, however, accommodate much less steep gradients, resulting from weaker sinks (Figure S7). We tested three cytokinin gradients in 1D models of WUS expression (where we only consider cytokinin as an activator and AHK repressor as a repressor). For a range a Hill coefficients, we show that both shallow and sharp cytokinin gradients can produce correct WUS domains, shallow gradients do, however, require higher Hill coefficients than steep gradients. Despite considering a strong sink may better reflect the meristem biology, WUS expression can be described without a sink, and the model conclusions are not dependent on the specific boundary condition implemented. Note, while the steepest gradient resembles our optimised gradient, the middle panel, showing a less steep gradient, more resembles the gradient suggested in a previous study, where the tissue was extended to a larger part of the plant (approximating a non-sink boundary,16). Finally, the last panel shows that an even shallower gradient will allow a WUS domain to be specified.
We further explored the impact of the sink on the rest of the model. To ease the comparison with previous figures, we fixed the cytokinin and AHK repressor gradients to the values used for Fig. 1d (pocket repressor), Fig. 3 and Fig. 6a. For all the other diffusing molecules in the system, we replaced the sink with a no flux boundary condition; these molecules are effectively “trapped” in the meristem and cannot diffuse to the tissues below. Even in this extreme scenario, opposing a sink, we could optimise the system and obtain parameter sets for each of the three categories described in the rest of the manuscript (Figure S8).
Altogether, these simulations show that the model is robust to the boundary condition selected to represent the connection between the meristem and the tissues below.
Data availability
Microscopy stacks for the pHAM1::YPET-N7 and pHAM2::YPET-N7 reporter lines can be found at: https://doi.org/10.17863/CAM.23438. Software for all the algorithms described and the resulting optimised parameter values are available at: http://gitlab.com/SLCU/TeamHJ/Jeremy/ham.
References
Steeves, T. A. & Sussex, I. M. Patterns in Plant Development. (Cambridge: Cambridge University Press, 1989).
Schoof, H. et al. The stem cell population of Arabidopsis shoot meristems in maintained by a regulatory loop between the CLAVATA and WUSCHEL genes. Cell 100, 635–644 (2000).
Laux, T., Mayer, K. F., Berger, J. & Jurgens, G. The WUSCHEL gene is required for shoot and floral meristem integrity in Arabidopsis. Development 122, 87–96 (1996).
Mayer, K. F. et al. Role of WUSCHEL in regulating stem cell fate in the Arabidopsis shoot meristem. Cell 95, 805–815 (1998).
Yadav, R. K. et al. WUSCHEL protein movement mediates stem cell homeostasis in the Arabidopsis shoot apex. Genes Dev. 25, 2025–2030 (2011).
Yadav, R. K. et al. Plant stem cell maintenance involves direct transcriptional repression of differentiation program. Mol. Syst. Biol. 9, 654 (2013).
Clark, S. E., Williams, R. W. & Meyerowitz, E. M. The CLAVATA1 gene encodes a putative receptor kinase that controls shoot and floral meristem size in Arabidopsis. Cell 89, 575–585 (1997).
Ogawa, M., Shinohara, H., Sakagami, Y. & Matsubayashi, Y. Arabidopsis CLV3 peptide directly binds CLV1 ectodomain. Science 319, 294 (2008).
Gordon, S. P., Chickarmane, V. S., Ohno, C. & Meyerowitz, E. M. Multiple feedback loops through cytokinin signaling control stem cell number within the Arabidopsis shoot meristem. Proc. Natl Acad. Sci. USA 106, 16529–16534 (2009).
Bartrina, I., Otto, E., Strnad, M., Werner, T. & Schmulling, T. Cytokinin regulates the activity of reproductive meristems, flower organ size, ovule formation, and thus seed yield in Arabidopsis thaliana. Plant Cell 23, 69–80 (2011).
Chickarmane, V. S., Gordon, S. P., Tarr, P. T., Heisler, M. G. & Meyerowitz, E. M. Cytokinin signaling as a positional cue for patterning the apical-basal axis of the growing Arabidopsis shoot meristem. Proc. Natl Acad. Sci. USA 109, 4002–4007 (2012).
Landrein, B. et al. Nitrate modulates stem cell dynamics in Arabidopsis shoot meristems through cytokinins. Proc. Natl Acad. Sci. USA, 0027–8424 (2018).
Gruel, J. et al. An epidermis-driven mechanism positions and scales stem cell niches in plants. Sci. Adv. 2, e1500989 (2016).
Hohm, T., Zitzler, E. & Simon, R. A dynamic model for stem cell homeostasis and patterning in Arabidopsis meristems. PLoS One 5, e9189 (2010).
Jönsson, H., Shapiro, B., Meyerowitz, E. & Mjolsness, E. in Signaling in multicellular models of plant development (eds. Kumar, S., & Bentley, P.) On Growth, Form and Computers. 156–161 (Academic Press, London, 2003).
Adibi, M., Yoshida, S., Weijers, D. & Fleck, C. Centering the Organizing Center in the Arabidopsis thaliana shoot apical meristem by a combination of cytokinin signaling and self-organization. PLoS One 11, e0147830 (2016).
Schulze, S., Schafer, B. N., Parizotto, E. A., Voinnet, O. & Theres, K. LOST MERISTEMS genes regulate cell differentiation of central zone descendants in Arabidopsis shoot meristems. Plant J. 64, 668–678 (2010).
Zhou, Y. et al. Control of plant stem cell function by conserved interacting transcriptional regulators. Nature 517, 377–380 (2015).
Shen-Orr, S. S., Milo, R., Mangan, S. & Alon, U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 31, 64–68 (2002).
Daum, G., Medzihradszky, A., Suzaki, T. & Lohmann, J. U. A mechanistic framework for noncell autonomous stem cell induction in Arabidopsis. Proc. Natl Acad. Sci. USA 111, 14619–14624 (2014).
Shea, M. A. & Ackers, G. K. The OR control system of bacteriophage lambda. A physical–chemical model for gene regulation. J. Mol. Biol. 181, 211–230 (1985).
Fletcher, J. C. & Meyerowitz, E. M. Cell signaling within the shoot meristem. Curr. Opin. Plant Biol. 3, 23–30 (2000).
Muller, R., Borghi, L., Kwiatkowska, D., Laufs, P. & Simon, R. Dynamic and compensatory responses of Arabidopsis shoot and floral meristems to CLV3 signaling. Plant Cell 18, 1188–1198 (2006).
Brand, U., Grunewald, M., Hobe, M. & Simon, R. Regulation of CLV3 expression by two homeobox genes in Arabidopsis. Plant Physiol. 129, 565–575 (2002).
Xin, W., Wang, Z., Liang, Y., Wang, Y. & Hu, Y. Dynamic expression reveals a two-step patterning of WUS and CLV3 during axillary shoot meristem formation in Arabidopsis. J. Plant Physiol. 214, 1–6 (2017).
Perales, M. et al. Threshold-dependent transcriptional discrimination underlies stem cell homeostasis. Proc. Natl Acad. Sci. USA 113, E6298–E6306 (2016).
Smyth, D. R., Bowman, J. L. & Meyerowitz, E. M. Early flower development in Arabidopsis. Plant Cell 2, 755–767 (1990).
Fernandez, R. et al. Imaging plant growth in 4D: robust tissue reconstruction and lineaging at cell resolution. Nat. Methods 7, 547–553 (2010).
Acknowledgements
We thank E. Meyerowitz for providing the HAM1/HAM2 reporter lines and members of the Jonsson and Meyerowitz (Caltech) groups for fruitful discussions. Work funded by the Gatsby Charitable Foundation. This work was supported by the Gatsby Charitable Foundation via grant GAT3395-PR4.
Author information
Authors and Affiliations
Contributions
J.G. devised the study, wrote the algorithms, analysed the data and wrote the manuscript. J.D. adapted the algorithms for the realistic template and optimised the model for it. B.L. obtained and analysed the experimental data. T.H. implemented the meristem shape and size deformations. H.J. devised the study and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gruel, J., Deichmann, J., Landrein, B. et al. The interaction of transcription factors controls the spatial layout of plant aerial stem cell niches. npj Syst Biol Appl 4, 36 (2018). https://doi.org/10.1038/s41540-018-0072-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41540-018-0072-1
This article is cited by
-
Promotive effect of phytosulfokine - peptide growth factor - on protoplast cultures development in Fagopyrum tataricum (L.) Gaertn
BMC Plant Biology (2023)
-
CLAVATA3 mediated simultaneous control of transcriptional and post-translational processes provides robustness to the WUSCHEL gradient
Nature Communications (2021)
-
What shoots can teach about theories of plant form
Nature Plants (2021)
-
Transcriptomic profiles of non-embryogenic and embryogenic callus cells in a highly regenerative upland cotton line (Gossypium hirsutum L.)
BMC Developmental Biology (2020)
-
A signal cascade originated from epidermis defines apical-basal patterning of Arabidopsis shoot apical meristems
Nature Communications (2020)