Abstract
Charge density waves (CDWs) in kagome metals have been tied to many exotic phenomena. Here, using spectroscopic-imaging scanning tunneling microscopy and angle-resolved photoemission spectroscopy, we study the charge order in kagome metal ScV6Sn6. The similarity of electronic band structures of ScV6Sn6 and TbV6Sn6 (where charge ordering is absent) suggests that charge ordering in ScV6Sn6 is unlikely to be primarily driven by Fermi surface nesting of the Van Hove singularities. In contrast to the CDW state of cousin kagome metals, we find no evidence supporting rotation symmetry breaking. Differential conductance dI/dV spectra show a partial gap Δ1CO ≈ 20 meV at the Fermi level. Interestingly, dI/dV maps reveal that charge modulations exhibit an abrupt phase shift as a function of energy at energy much higher than Δ1CO, which we attribute to another spectral gap. Our experiments reveal a distinctive nature of the charge order in ScV6Sn6 with fundamental differences compared to other kagome metals.
Similar content being viewed by others
Introduction
The kagome lattice, a pattern of tessellated hexagons connected by small corner-sharing triangles, emerged as a versatile platform for exploring a variety of novel quantum phases of matter. Due to the geometric frustration intrinsic to the kagome lattice, layered kagome materials are characterized by a characteristic electronic band structure consisting of Dirac fermions, flat bands and Van Hove singularities (VHSs)1,2,3,4,5. This prototypical band structure can be intertwined with a rich array of exotic electronic instabilities, which have been theoretically explored and experimentally realized in several families of kagome metals thus far. For example, Fe-6,7,8,9,10,11,12,13,14,15, Mn-16,17,18,19,20,21 and Co-22,23,24,25 based kagome magnets yielded the realization of topological flat bands11,23,26, Dirac and Weyl fermions6,9,12,22,24,27 and Fermi arcs22,24; a non-magnetic V-based AV3Sb5 (A = Cs, K, Rb) kagome metal family28,29,30 on the other hand attracted a large interest31,32,33,34,35,36,37,38,39,40,41 due to the emergence of superconductivity and various symmetry-breaking states including charge density waves potentially in connection to loop current orders42.
The recently discovered bilayer kagome metals in the RV6Sn6 structure (166 family), where R stands for a rare earth ion, offer a new tunable platform to investigate Fermi surface instabilities of the kagome lattice43,44,45,46,47,48. Similarly to that in AV3Sb5, vanadium atoms that comprise the kagome layers in RV6Sn6 remain non-magnetic44,45,46,49, but magnetism can still be selectively tuned by the choice of the rare earth element R49,50,51. Out of the wide array of kagome metals in the RV6Sn6 structure, ScV6Sn6 presents a unique platform where a charge density wave (CDW) state was reported below TCDW ≈ 92 K46. In contrast to the CDW ordering wave vector in the AV3Sb5 family that connects the M points, which satisfies the nesting condition between VHSs at M and corresponds to the natural breathing modes of the kagome lattice, the ordering wave vector of the charge order (CO) in ScV6Sn6 connects the K points, time-reversal invariant points where the Dirac nodes are formed. Similar to the bulk CDW phase in AV3Sb5, the CO phase in ScV6Sn6 is also three-dimensional but now with a different wave vector Q*= (1/3, 1/3, 1/3) and rotated 30 degrees with respect to the hexagonal lattice directions. Recent studies further report time-reversal symmetry breaking from muon spectroscopy experiments52 and anomalous Hall effect from transport measurements53, both concomitant with the onset of the CO phase despite the absence of spin magnetism. Understanding the formation of the CO in ScV6Sn6 and how it compares to the more intensely investigated CDW in AV3Sb5 has been of high interest, but very little is known about its origin and associated spectroscopic fingerprint.
Here we use a combination of scanning tunneling microscopy/spectroscopy (STM/S) and angle-resolved photoemission spectroscopy (ARPES) to investigate the electronic structure and the CO formation in ScV6Sn6. STM topographs reveal a √3×√3 R30° electronic superstructure, which corresponds to the in-plane component of the bulk CO wavevector identified in diffraction measurements. In contrast to the C2-symmetric CDW state in AV3Sb5, we discover that the electronic structure of the CO state of ScV6Sn6 does not show the same unidirectionality. Our low-temperatures ARPES measurements reveal that the electronic structure of ScV6Sn6 (with the CO) shares much in common with that of TbV6Sn6 (without the CO), thus making the purely Fermi-surface-nesting-driven mechanism of the CO unlikely. We uncover the temperature evolution of the electronic bands in the vicinity of the K-point, which is consistent with the modulation of the surface bands in first-principle calculations as a consequence of the CO. Differential conductance maps reveal that CO modulations exhibit a spatial phase shift, a so-called contrast inversion, away from zero energy. In other materials, contrast inversion has been associated with underlying spectral gaps. Here we find that the energy scale of the contrast inversion is incompatible with the dominant spectral gap from DFT calculations or the small gap at the Fermi level in our dI/dV spectra. Given that mounting theoretical evidence suggests the importance of a Dirac node near Fermi level in the formation of the √3×√3 CO, we hypothesize that the contrast inversion energy scale is potentially related to a CO gap on the Dirac cone at K, which could point to a fundamentally different CO mechanism in ScV6Sn6 compared to other kagome metals.
Results
Microscopic visualization of the CO structure
Crystal structure of ScV6Sn6 is composed of layers of V atoms arranged on a kagome network, each stacked between a ScSn3 layer and a Sn1-Sn2-Sn1 trilayer (Fig. 1a, b). We study bulk single crystals of ScV6Sn6 grown by a flux-based method (Methods), which exhibit the characteristic kink in the magnetization measurements associated with the onset of the CO (Fig. 1d). We cleave the bulk single crystals in ultra-high vacuum to expose a pristine surface before measurements (Methods). Related materials in the same crystal structure tend to cleave along the c-axis to reveal ab-plane surface terminations19,20,27,43,45,47. This is consistent with the observed surface structure of UHV-cleaved ScV6Sn6 – STM topographs exhibit a hexagonal lattice (Fig. 1e–h) and the occasionally observed steps are an integer number of c-axis unit cell heights (Fig. 1c, Supplementary Fig. 7). STM topographs show two types of surface morphologies, both with a hexagonal lattice (Fig. 1e, g, Supplementary Fig. 1, Supplementary Fig. 2). We identify the termination in Fig. 1e as the Sn2 termination due to the clearly resolved individual atoms forming a hexagonal lattice (top inset in Fig. 1e) similar to the Sn2 surface imaged in YMn6Sn620. The surface termination in Fig. 1g is likely the kagome layer, as we deem the other two possibilities, Sn1 and ScSn3, to be unlikely: the Sn1 termination in YMn6Sn6 showed a triangular atomic structure20 and the surface equivalent to ScSn3 termination in TbMn6Sn6 appears to have a tendency to reconstruct into stripe-like features as reported in ref. 27.
a The schematic of the bulk crystal structure of ScV6Sn6, and (b) ab-plane surface atomic structure. c Topographic linecut showing single steps between consecutive Sn2 terraces taken along the red line in the inset. Inset in c shows an STM topograph spanning several consecutive steps. d Magnetization measurements (zero-field cooled, then taken at 1 T applied in the ab-plane warming up) showing a kink at T* associated with the bulk transition. STM topographs of (e) Sn2 termination and (g) kagome termination, and (f, h) associated Fourier transforms. Atomic Bragg peaks are circled in black; CO peaks are enclosed in green circles, red squares and blue triangles. STM setup conditions: (c) Iset = 10 pA, Vsample = 1 V; (e) Iset = 400 pA, Vsample = 20 mV; (g) Iset = 200 pA, Vsample = 200 mV. Scale bars correspond to: (e, g) 4 nm; (f, h) 1 Å−1.
In addition to the atomic Bragg peaks QiBragg (i = a, b or c), Fourier transforms (FTs) of STM topographs of the V kagome termination show six additional superlattice peaks (Fig. 1h). These FT peaks are positioned exactly along each Γ-K direction at Q* = (QiBragg+QjBragg)/3 (i, j = a, b or c) and are symmetric with respect to the center of the FT. They correspond to the staggered intensity modulations seen in real-space in STM topographs (inset in Fig. 1g). To investigate the origin of these modulations, we examine the energy dependence of the associated wave vectors in the FTs of differential conductance dI/dV(r,V) maps (Fig. 2a–d) and associated dI/dV spectra (Fig. 2e, f). On the kagome termination, the FT peaks are discernable in a wide range of energies e·V and the peak positions in momentum-transfer space are independent of the bias V (Fig. 2c). Moreover, the peak position is exactly consistent with the in-plane component of the newly discovered CO phase detected in diffraction experiments46. Therefore, the charge modulations observed in the STM topograph in Fig. 1g represent a microscopic visualization of the bulk CO state at the surface of this system. To confirm the three-dimensional nature of the CO, we study the charge modulations across a step edge, where we observe a phase shift of modulation peaks between the two adjacent terraces consistent with the expected bulk CO structure46 (Supplementary Fig. 7, Supplementary Note 2). Differential conductance dI/dV spectra on the kagome surface termination show a gap-like feature, with a partial suppression in the density-of-states of about 20 meV (Fig. 2e). As the CO is the only known ordered state in this system, we deem that the gap is likely related to the emergent CO. Interestingly, the observed gap is much smaller than the CDW gap observed in dI/dV spectra of AV3Sb5 and FeGe of about 40–50 meV31,34,35,54, despite the comparable TCDW temperatures in the two systems.
a Differential conductance dI/dV(r, V = 50 mV) map acquired over the kagome termination, and (b) associated Fourier transform (FT). c Energy-dependent FT linecuts of dI/dV(r, V) maps of the kagome termination, starting at the FT center along the three Γ-K directions (labeled as qa, qb and qc in b). Non-dispersive CO peaks are observed along all three directions. d Energy-dependent FT linecuts of dI/dV(r, V) maps of the Sn2 termination, starting at the FT center along the three Γ-K directions. No additional peaks are observed at the same momentum-transfer position where the CO peaks are seen on the kagome termination. Small vertical arrows above the top panel in (c, d) denote the position where the CO peak is expected. Average dI/dV spectra (solid line and circle symbols) over (e) the kagome and (f) Sn2 termination. Diffuse orange (blue) background shows representative dI/dV spectra taken over several linecuts in the same field-of-view on kagome (Sn2) surface. STM setup conditions: (a) Iset = 50 pA, Vsample = 50 mV, Vexc = 4 mV; (c) Iset = 30 pA, Vsample = –100 mV, Vexc = 5 mV; (d) Iset = 200 pA, Vsample = 50 mV, Iset = 2 mV; (e) Iset = 30 pA, Vsample = 50 pA, Vexc = 3 mV; (f) Iset = 200 pA, Vsample = 50 mV, Vexc = 1 mV. Scale bars correspond to: (a) 4 nm; (b) 1 Å–1.
Spectroscopic investigation of the nature of the CO
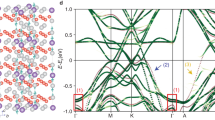
Having identified the real-space signatures of the CO in ScV6Sn6, we next turn to the momentum-space evidence. ARPES has been an extremely useful tool in determining the signature kagome bands14,40,55,56,57,58, the CDW gap modulation and the band reconstruction associated with CDW order57,58,59 in AV3Sb5 and FeGe where CDWs have been reported thus far. We first show the measured Fermi surface (FS) of ScV6Sn6 obtained on the kagome termination (see Supplementary Note 1, Supplementary Fig. 3). The FS consists of segments connecting the M points of the Brillouin zone (BZ) (Fig. 3a), similar to that of other kagome metals such as AV3Sb529,40,57,59 and FeGe14,58. Figure 3b, c shows the dispersions measured along the high symmetry direction Γ-K-M, acquired using beams of linear horizontal (LH) and linear vertical (LV) polarizations, respectively. We observe a quadratic band centered at Γ, with the band bottom located at about 1 eV below the Fermi level, EF. This band extends to the M point in the form of a VHS near EF (Fig. 3c). This is consistent with the typical band structure associated with the kagome lattice, and also matches well with the band structure calculated by the density-functional theory (DFT) (Fig. 3d), suggesting weak electron-electron correlation effects. Since both ScV6Sn6 and TbV6Sn6 share the same V kagome layer, we proceed to compare the band structures of the two systems. Both the FS and band dispersions show a striking similarity (Fig. 3a–c, Fig. 3e–g). In particular, the locations of the VHS at M are very close to EF in both systems, with that in ScV6Sn6 slightly below EF and that in TbV6Sn6 slightly above EF (Fig. 3c, g). The small difference in VHS positions is also consistent with the DFT calculations (Fig. 3d, h).
a Fermi surface map of ScV6Sn6 overlaid with the 2D BZ. b, c Dispersions acquired along the high-symmetry direction Γ-K-M, with the polarization LH and LV + \(\odot\), respectively. Here LH and LV are defined as the in-plane component along the horizontal and vertical directions of the image. When there is an out-of-plane contribution due to experimental setup, we denote it by +⊙. The red dashed line serves as a guide to the eye for the band forming the VHS near EF. d Band structure of ScV6Sn6 in the pristine phase calculated by DFT. e–h Data (83 eV photon energy) and DFT calculations of TbV6Sn6 corresponding to each panel of ScV6Sn6 above.
To investigate the effect of the CO on the electronic structure of ScV6Sn6, we perform temperature-dependent measurements of dispersions along the Γ-K-M direction (one such plot acquired at 20 K shown in Fig. 4a) across the transition T* ≈ 92 K46. To reveal the band reconstruction, we present a series of normalized intensity plots, showing the subtracted difference between the cuts taken at selected temperatures and that taken at 120 K > T* (Fig. 4b) (see Supplementary Fig. 4). The most substantial difference appears in the vicinity of the K points near EF, seen as patches of blue on these color maps, and disappears above about 100 K (Fig. 4b). This difference can also be clearly seen by comparing the energy distribution curves (EDCs) taken at 20 K and 120 K in the region across the K point, where we discover a prominent spectral weight shift towards EF on the side of the K point closer to the M point (upper half of Fig. 4c). The temperature evolution of the spectral weight change can also be seen in the collapsed stack of integrated EDCs in this momentum-space region (Fig. 4d). To quantitatively determine the temperature dependence of the spectral weight shift, we plot the peak area of this EDC integrated between -0.2 V and EF (Fig. 4d, e). The peak area decreases as the temperature increases, with an abrupt change of the slope within a temperature window of ~15 K across T* (Fig. 4e), consistent with the transition observed. The abrupt drop of the peak area is consistent with a first-order nature of the phase transition46.
a Γ-K-M cut in the vicinity of EF taken at 20 K. b Subtraction between cuts measured at selected temperatures and that at 120 K, with the energy and momentum range same as (a). The intensity is such that white represents zero, indicating no change. c EDC comparison taken at 20 K and 120 K in the region denoted by the dark blue bar in (a). d Stacked EDCs as a function of temperature acquired in the region between K and M. e Integrated peak area of each curve in (d) between –0.2 eV and EF, plotted as a function of temperature. Grey shade covers the temperature range where an abrupt drop of peak area occurs. The red dashed line indicates T*. f Bulk band structure calculated by DFT, in the pristine phase (upper) and the CO phase (lower). g Surface bands in the pristine and the CO phase calculated by DFT. The blue arrow points to the gap opening (see text). h Schematic of the surface and bulk BZs. Dark blue and light blue arrows correspond to qCO,surface and qCO,bulk, respectively. i Direct comparison of ARPES data, pristine surface bands and the surface bands in the CO state, and the schematic showing the origin of the spectral weight shift.
To understand the origin of the band reconstruction near the K points, we perform DFT calculations for the CDW state. We first present the DFT calculations for the bulk bands along Γ-K-M (Fig. 4f). Note that the CDW band structure has been unfolded back into the pristine BZ for ease of comparison. Comparing the pristine and CDW calculations, we observe little difference near the K point. This can be understood as the three-dimensional CDW wavevector (1/3, 1/3, 1/3) corresponds to a reduction of the pristine BZ to a smaller one, where the pristine K and K’1/3 (the point at 1/3 along K’-H’) points are now equivalent in the reconstructed BZs (Fig. 4h). However, DFT calculations for bulk states predict no states in the vicinity of H point near EF in the pristine phase (Supplementary Fig. 5, Methods), which would lead to negligible folding between K and K’1/3 points. Hence, the band reconstruction we observe near the K point is unlikely to be directly due to bulk band folding. However, when the surface states are subject to the CDW folding potential, they would fulfill the in-plane folding condition Q*in-plane = (QaBragg+QbBragg)/3, folding states between the K’ and K points. We carried out DFT calculations for the surface states on the kagome termination under the bulk CDW wavevector (1/3, 1/3, 1/3). Indeed, folded bands and gap openings appear near the K point (Fig. 4g). Specifically, immediately below EF at K, a band crossing opens a gap and the upper branch is pushed towards EF (blue arrow in Fig. 4g). This is consistent with the spectral weight shift towards EF we observe at the K point (Fig. 4i).
Absence of rotational symmetry breaking in the CO state of ScV6Sn6
To fully understand any electronic phase in a material, it is crucial to determine which symmetries are broken and which are preserved. In the CDW phase of AV3Sb5, an array of experimental techniques observed signatures of in-plane rotational symmetry breaking, which first onsets at the TCDW temperature37,60,61 and reduces the in-plane rotational symmetry from six-fold to twofold31,32,35,37,60,61,62. We proceed to explore whether the rotational symmetry of the kagome bilayer in ScV6Sn6 is also broken. For pedagogical purposes, we first discuss the experiments on KV3Sb5. Similarly to the analysis done in refs. 35,60,62, we compare the CDW amplitudes along the three inequivalent directions as a function of energy (Fig. 5c). A noticeable difference in the CDW amplitude dispersions is clearly observed between different peaks, with one direction being markedly different from the other two that are nearly the same. This FT peak anisotropy is also reflected in the unidirectionality of the pattern in dI/dV(r,V) maps (Fig. 5d). In ScV6Sn6 however, we find that the shape of the CO amplitude dispersions versus energy along the three directions is nearly identical (Fig. 5a). We note that tiny differences between the three curves reflect the measurement and analysis uncertainty, as well as the inevitable small STM tip anisotropy. The approximately rotationally symmetric CO signature can also be seen in representative dI/dV(r,V) maps (Fig. 5b). This conclusion is further reinforced by equivalent analysis conducted in a separate region with a microscopically different tip, which yielded consistent results (Supplementary Fig. 11). These measurements suggest the absence of rotation symmetry reduction from C6 to C2 associated with the CO in ScV6Sn6.
a Energy-dependent amplitudes of the three inequivalent CDW peaks (marked in the example Fourier transform in the inset) in ScV6Sn6. The overall shape of all three dispersion curves is nearly identical and largely overlaps one another. b Zoom-in on representative high-resolution dI/dV(r, V) maps showing the approximately rotationally symmetric real-space signature. c Energy-dependent amplitudes of the three inequivalent CDW peaks (marked in the example Fourier transform in the inset) in cousin kagome metal KV3Sb5. the dispersion of Qc amplitude is noticeably different than the other two, Qa and Qb, that are nearly indistinguishable. d Representative dI/dV(r, V) maps showing a unidirectional real-space signature that breaks the six-fold symmetry. STM setup conditions: (a) Iset = 30 pA, Vsample = -100 mV, Vexc = 5 mV; (b) Iset = 100 pA, Vsample = 100 mV, Vexc = 2 mV; (c, d) Iset = 150 pA, Vsample = 10 mV, Vexc = 1 mV. Scale bars correspond to: (b) 1 nm; (d) 4 nm.
Unusual charge modulation contrast reversal away from Fermi level
In the classical Peierls scenario, the CDW-induced spectral gap opening at the Fermi level is accompanied by charge modulations that are out-of-phase in occupied and unoccupied electronic states. This contrast inversion can be seen in STM data – locations of charge accumulation below Fermi level will correspond to charge depletion above Fermi level, and vice versa. It is considered one of the hallmarks of the CDW state seen in many materials63,64, including the cousin CDW kagome systems AV3Sb531. To test this, we examine and compare STM topographs, which contain information on integrated density-of-states from Fermi level to the energy corresponding to the imaging bias, acquired over identical regions of the sample but at different polarities of bias. We find that STM topographs at +200 mV and –200 mV indeed show the charge modulation contrast reversal (Fig. 6a–d). This is especially apparent in the Fourier-filtered zoomed-in regions, aligned with atomic-registry using the process of drift-correction, where we can see that high-conductance features at one bias polarity correspond to low-conductance features at the opposite bias (Fig. 6e, f).
a, b STM topographs acquired at opposite bias polarities, drift-corrected and aligned to be over the exact same area with atomic-registry. Small black and red squares in (a, b) mark an identical region of the sample in the two topographs. c, d Zoom-in over the two small squares in (a, b), and (e, f) Fourier-filtered (FT-filtered) images that only contain the CO Fourier peaks. Triangles in (c, f) mark the same location of the sample connecting three dark checkers (dashed line) or three bright checkers (solid line). g Differential conductance dI/dV(r, V) maps at different bias showing contrast reversal between +40 mV and +100 mV bias. Importantly there is no contrast reversal between –40 mV and +40 mV maps. STM setup conditions: (a, c) Iset = 50 pA, Vsample = –200 mV; (b, d) Iset = 100 pA, Vsample = 200 mV; (g) Iset = 100 pA, Vsample = 100 mV, Vexc = 2 mV. Scale bars correspond to: (a, b) 4 nm.
Interestingly however, STM topographs at lower bias show a striking asymmetry in the CO signal. In particular, while the topograph at –100 mV still shows visible CO modulations, the CO in the +100 mV topograph becomes difficult to discern (Supplementary Fig. 8). This bias dependence is highly unusual. To gain further insight into this behavior, we turn to differential conductance dI/dV(r,V) maps in this bias range (Fig. 6g). The maps acquired at negative bias all show the same phase of CO (Fig. 6g). The trend continues for small positive bias, but flips around 60–80 mV (Fig. 6g, Supplementary Fig. 9). Such contrast inversion away from the Fermi level is unexpected given the small spectral gap detected at the Fermi level. The absence of contrast inversion at the Fermi level is also confirmed in STM topographs obtained at ±20mV (Supplementary Fig. 10). This is in striking contrast to the CO contrast inversion in AV3Sb5 reported to occur at low bias near the Fermi level31, and in general, suggests an unusual nature of the CO in ScV6Sn6.
Discussion
Our experiments provide the microscopic visualization of the CO phase in ScV6Sn6 and associated spectroscopic fingerprints, and have several important implications. First, they enable a comparison of the role of VHSs in the CO formation between different families of kagome metals. The VHSs have now been observed at the M points of the BZ near EF in both ScV6Sn6 and TbV6Sn6, as well as AV3Sb5 and FeGe. In AV3Sb5 and FeGe, it is natural to relate the 2 × 2 CDW order to the FS nesting as the wavevector in principle fulfills the nesting condition. However, in the present case of ScV6Sn6, while the VHSs remain close to EF at the M point, the CO wave vector is no longer compatible with the same FS nesting wave vectors, which suggests a non-VHS-nesting origin of the CO in ScV6Sn6. This is further supported by the similarities in the fermiology of ScV6Sn6 and TbV6Sn6, and the contrasting presence of the CO in the former and the absence in the latter.
Our experiments also reveal a surprising surface termination dependence of the three-dimensional bulk CO. While charge modulations are clearly observed on the kagome termination, Sn2 surface termination does not show the CO in either the topograph or dI/dV(r,V) maps near EF. Correspondingly, the small spectral gap in dI/dV spectra on the kagome termination is absent on the Sn termination (Fig. 2e, f). Since DFT calculations46,65 and X-ray diffraction46,66,67 suggest that atoms in the two layers, V and Sn2, are not expected to show substantial atomic displacements, our measurements suggest layer-dependent variation of the charge density. These observations should be relevant for other surface sensitive studies, which should take into account the unusual termination dependence of the bulk order in this system. For comparison, the 2 ×2 CDW state in AV3Sb5 as well as FeGe can be detected in STM/S measurements of both surface terminations imaged31,32,34,35,54.
From the symmetry perspective, the CO in Sc-166 is also distinct from other kagome metals. In particular, while the CO in ScV6Sn6 breaks the translational symmetry of the lattice, the rotational symmetry appears to be preserved. This is in contrast to AV3Sb5, where rotation symmetry breaking occurs concomitant with the CDW onset37,60,61. It is conceivable that rotation symmetry breaking in AV3Sb5 is then related to the unusual orbital picture as recently evidenced in isostructural CsTi3Bi568,69.
Lastly, the CO contrast inversion observed at positive energies provides additional insights. In the classical Peierls scenario, the contrast inversion appears between the two sides of the spectral gap centered at the Fermi level. CO contrast inversions away from the zero energy are seldom reported, but in these rare cases, they have been attributed to hidden spectral gaps away from the Fermi level that are difficult to resolve in dI/dV spectra70,71. In ScV6Sn6, DFT calculations predict several gaps in the CO state, with by far the largest one of more than 200 meV occurring primarily at negative energies along the L – A direction65. However, the energy position of the CO contrast inversion is incompatible with either the large DFT-predicted gap or the small gap at the Fermi energy detected in our data. This brings a natural question of the reason behind the unexpected contrast inversion at positive energy.
The BZ K point is of special significance in ScV6Sn6. First, the neighboring K points are connected exactly by the wave vector of the CO. Second, DFT calculations of the phonon spectra indicate the presence of phonon softening also at the K points65. Third, mounting theoretical work demonstrated the importance of the proximity of a Dirac point at K near zero energy in stabilizing the √3×√3 CDW order on a kagome lattice72,73,74. In particular, a recent Monte-Carlo study suggests that electron-phonon coupling and the Dirac node at K positioned near Fermi level are both necessary ingredients for the formation of the CO state74. ScV6Sn6 indeed shows at least one Dirac point in the vicinity of the Fermi level65 (Fig. 3). Given that other prominent band gaps in Sc-166 are incompatible with the CO contrast inversion observed, it is conceivable that the contrast inversion here is governed by the gapped Dirac dispersion at K. In this scenario, the combination of the favorable Dirac cone placement and phonon softening at K may play a key role in the CO formation, a mechanism possibly realized experimentally here in ScV6Sn6. Our experiments also demonstrate the existence of multiple spectral gaps, thus highlighting a generic, yet often overlooked feature of the charge-ordered systems. Taken all evidence together, our results reveal not only a distinctive nature of the CO in ScV6Sn6 in comparison to other kagome metals, but also point to a paradigm shift of the CO realization driven by the presence of Dirac nodes at K and structural instabilities, as opposed to VHSs at M. This further provides a plausible guiding principle for searching for equivalent COs in other systems, rooted in similar characteristic electronic band structure and structural instabilities at K.
Methods
Single crystal growth and characterization
Single crystals of ScV6Sn6 were grown from Sc (pieces, 99.9%), V (pieces, 99.7%), and Sn (shots, 99.99%) via a flux-based growth technique. The flux mixture of Sc, V and Sn was loaded inside an alumina crucible with a molar ratio of 1:6:40 and then heated at 1125 °C for 12 h. Then, the mixture was cooled at a rate of 2 °C hr–1 to 780 °C and centrifuged to separate the single crystals from the excess Sn-flux.
STM experiments
Single crystals of ScV6Sn6 were cleaved in ultrahigh vacuum and inserted into the STM head at 4.5 K. All STM measurements were taken at about 4.5 K, using home-made electrochemically etched tungsten tips annealed in UHV before STM experiments. STM data were acquired using a customized Unisoku USM1300 STM system. Spectroscopic measurements were made using a standard lock-in technique with 910-Hz frequency and bias excitation as noted in the figure captions.
Angle-resolved photoemission spectroscopy (ARPES) experiments
ARPES measurements on ScV6Sn6 were performed at the QMSC beamline of the Canadian Light Source, equipped with a R4000 electron analyzer, and TbV6Sn6 at Stanford Synchrotron Radiation Lightsource (SSRL), Beamline 5-2, equipped with a DA30 electron analyzer. The single crystals were cleaved in-situ at 20 K and measured in ultra-high vacuum with a base pressure better than 6 × 10–11 Torr. Energy and angular resolution were set to be better than 20 meV and 0.1°, respectively (Supplementary Fig. 6).
Density-functional theory (DFT) calculations
All calculations of ScV6Sn6 are performed within the DFT implemented in the Vienna ab-initio Simulation Package (VASP)75. The generalized gradient approximation as parameterized by Perdew, Burke, and Ernzerhof76 is employed for the exchange-correlation interaction between electrons. The energy cutoff for the plane wave basis set is 300 eV. A force convergence criterion of 1 meV Å−1 is used in the structural relaxation. The bulk Brillouin zone of the pristine ScV6Sn6 is sampled with a k-mesh of 21 × 21 × 10. The surface states of both the pristine phase and the CDW phase are simulated with slabs of 8 kagome layers thick, and obtained by projecting the slab band structure onto the surface unit cell. Spin-orbital coupling is not considered for both the bulk band structure and in slab calculations.
The DFT calculations on TbV6Sn6 are performed using a full-potential linear augmented plane wave (FP-LAPW) method, as implemented in WIEN2k77. Considering that Tb moments are disordered above 4 K and occupied Tb-4f states are far below the Fermi level, we treat 4 f electrons as non-magnetic core states in the open-core approach. The generalized gradient approximation of Perdew, Burke, and Ernzerhof76 is used for the correlation and exchange potentials. To generate the self-consistent potential and charge, we employed RMT×Kmax = 8.0 with muffin-tin (MT) radii RMT = 2.7, 2.4, and 2.5 a.u., for Tb, V, and Sn, respectively. The calculations are iterated until charge differences between consecutive iterations are smaller than 10−3 e and the total energy differences are lower than 0.01 mRy with 264 k-points in the irreducible Brillouin zone (IBZ). Experimental lattice parameters45 are employed, and spin-orbit coupling is included using a second variational method.
Data availability
Original data can be downloaded at https://doi.org/10.5281/zenodo.10459513 and it is also available upon request from the corresponding authors.
References
Sachdev, S. Kagome- and triangular-lattice Heisenberg antiferromagnets: Ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys. Rev. B 45, 12377–12396 (1992).
Guo, H.-M. & Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 80, 113102 (2009).
Mazin, I. I. et al. Theoretical prediction of a strongly correlated Dirac metal. Nat. Commun. 5, 4261 (2014).
Tang, E. & Fu, L. Strain-induced partially flat band, helical snake states and interface superconductivity in topological crystalline insulators. Nat. Phys. 10, 964–969 (2014).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional Quantum Hall States at Zero Magnetic Field. Phys. Rev. Lett. 106, 236804 (2011).
Ye, L. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018).
Yin, J.-X. X. et al. Giant and anisotropic many-body spin–orbit tunability in a strongly correlated kagome magnet. Nature 562, 91–95 (2018).
Ye, L. et al. de Haas-van Alphen effect of correlated Dirac states in kagome metal Fe3Sn2. Nat. Commun. 10, 4870 (2019).
Kang, M. et al. Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 19, 163–169 (2020).
Lin, Z. et al. Dirac fermions in antiferromagnetic FeSn kagome lattices with combined space inversion and time-reversal symmetry. Phys. Rev. B 102, 155103 (2020).
Lin, Z. et al. Flatbands and Emergent Ferromagnetic Ordering in Fe3Sn2 Kagome Lattices. Phys. Rev. Lett. 121, 096401 (2018).
Ren, Z. et al. Plethora of tunable Weyl fermions in kagome magnet Fe3Sn2 thin films. npj Quantum Mater. 7, 109 (2022).
Chen, T. et al. Large anomalous Nernst effect and nodal plane in an iron-based kagome ferromagnet. Sci. Adv. 8, 1–8 (2022).
Teng, X. et al. Discovery of charge density wave in a kagome lattice antiferromagnet. Nature 609, 490–495 (2022).
Li, H. et al. Spin-polarized imaging of the antiferromagnetic structure and field-tunable bound states in kagome magnet FeSn. Sci. Rep. 12, 14525 (2022).
Zhang, H. et al. Topological magnon bands in a room-temperature kagome magnet. Phys. Rev. B 101, 100405 (2020).
Wang, Q. et al. Field-induced topological Hall effect and double-fan spin structure with a c-axis component in the metallic kagome antiferromagnetic compound YMn6Sn6. Phys. Rev. B 103, 014416 (2021).
Ghimire, N. J. et al. Competing magnetic phases and fluctuation-driven scalar spin chirality in the kagome metal YMn6Sn6. Sci. Adv. 6, eabe2680 (2020).
Li, M. et al. Dirac cone, flat band and saddle point in kagome magnet YMn6Sn6. Nat. Commun. 12, 3129 (2021).
Li, H. et al. Manipulation of Dirac band curvature and momentum-dependent g factor in a kagome magnet. Nat. Phys. 18, 644–649 (2022).
Ma, W. et al. Rare Earth Engineering in RMn6Sn6 (R=Gd−Tm, Lu) Topological Kagome Magnets. Phys. Rev. Lett. 126, 246602 (2021).
Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).
Yin, J.-X. et al. Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet. Nat. Phys. 15, 443–448 (2019).
Liu, D. F. et al. Magnetic Weyl semimetal phase in a Kagomé crystal. Science 365, 1282–1285 (2019).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Kang, M. et al. Topological flat bands in frustrated kagome lattice CoSn. Nat. Commun. 11, 4004 (2020).
Yin, J.-X. X. et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020).
Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5 and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).
Ortiz, B. R. et al. CsV3Sb5: A Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Kenney, E. M., Ortiz, B. R., Wang, C., Wilson, S. D. & Graf, M. J. Absence of local moments in the kagome metal KV3Sb5 as determined by muon spin spectroscopy. J. Phys. Condens. Matter 33, 235801 (2021).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353–1357 (2021).
Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222–228 (2021).
Liang, Z. et al. Three-dimensional charge density wave and surface-dependent vortex-core states in a Kagome superconductor CsV3Sb5. Phys. Rev. X 11, 031026 (2021).
Li, H. et al. Rotation symmetry breaking in the normal state of a kagome superconductor KV3Sb5. Nat. Phys. 18, 265–270 (2022).
Mielke, C. et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature 602, 245–250 (2022).
Xu, Y. et al. Three-state nematicity and magneto-optical Kerr effect in the charge density waves in kagome superconductors. Nat. Phys. 18, 1470–1475 (2022).
Yang, S.-Y. et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5. Sci. Adv. 6, eabb6003 (2020).
Wu, X. et al. Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A=K, Rb, Cs). Phys. Rev. Lett. 127, 177001 (2021).
Kang, M. et al. Twofold van Hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys. 18, 301–308 (2022).
Guo, C. et al. Switchable chiral transport in charge-ordered kagome metal CsV3Sb5. Nature 611, 461–466 (2022).
Neupert, T., Denner, M. M., Yin, J.-X., Thomale, R. & Hasan, M. Z. Charge order and superconductivity in kagome materials. Nat. Phys. 18, 137–143 (2022).
Peng, S. et al. Realizing Kagome band structure in two-dimensional Kagome surface states of RV6Sn6 (R=Gd, Ho). Phys. Rev. Lett. 127, 266401 (2021).
Pokharel, G. et al. Electronic properties of the topological kagome metals YV6Sn6 and GdV6Sn6. Phys. Rev. B 104, 235139 (2021).
Rosenberg, E. et al. Uniaxial ferromagnetism in the kagome metal TbV6Sn6. Phys. Rev. B 106, 115139 (2022).
Arachchige, H. W. S. et al. Charge density wave in kagome lattice intermetallic ScV6Sn6. Phys. Rev. Lett. 129, 216402 (2022).
Hu, Y. et al. Tunable topological Dirac surface states and van Hove singularities in kagome metal GdV6Sn6. Sci. Adv. 8, eadd2024 (2022).
Zhang, X. et al. Destabilization of the charge density wave and the absence of superconductivity in ScV6Sn6 under high pressures up to 11 GPa. Mater. (Basel) 15, 7372 (2022).
Pokharel, G. et al. Highly anisotropic magnetism in the vanadium-based kagome metal TbV6Sn6. Phys. Rev. Mater. 6, 104202 (2022).
Lee, J. & Mun, E. Anisotropic magnetic property of single crystals RV6Sn6 (R=Y, Gd−Tm, Lu). Phys. Rev. Mater. 6, 083401 (2022).
Zhang, X. et al. Electronic and magnetic properties of intermetallic kagome magnets RV6Sn6 (R=Tb−Tm). Phys. Rev. Mater. 6, 105001 (2022).
Guguchia, Z. et al. Hidden magnetism uncovered in charge ordered bilayer kagome material ScV6Sn6. Nat. Commun. 14, 7796 (2023).
Yi, C. et al. Charge density wave induced anomalous Hall effect in kagome ScV6Sn6. Preprtint at: https://doi.org/10.48550/arXiv.2305.04683 (2023).
Yin, J.-X. et al. Discovery of charge order and corresponding edge state in Kagome magnet FeGe. Phys. Rev. Lett. 129, 166401 (2022).
Luo, J. et al. Possible star-of-David pattern charge density wave with additional modulation in the kagome superconductor CsV3Sb5. npj Quantum Mater. 7, 30 (2022).
Hu, Y. et al. Topological surface states and flat bands in the kagome superconductor CsV3Sb5. Sci. Bull. 67, 495–500 (2022).
Kang, M. et al. Charge order landscape and competition with superconductivity in kagome metals. Nat. Mater. 22, 186–193 (2023).
Teng, X. et al. Magnetism and charge density wave order in kagome FeGe. Nat. Phys. 19, 814–822 (2023).
Luo, H. et al. Electronic nature of charge density wave and electron-phonon coupling in kagome superconductor KV3Sb5. Nat. Commun. 13, 273 (2022).
Li, H. et al. Unidirectional coherent quasiparticles in the high-temperature rotational symmetry broken phase of AV3Sb5 kagome superconductors. Nat. Phys. 19, 637–643 (2023).
Xiang, Y. et al. Twofold symmetry of c-axis resistivity in topological kagome superconductor CsV3Sb5 with in-plane rotating magnetic field. Nat. Commun. 12, 6727 (2021).
Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Mallet, P., Sacks, W., Roditchev, D., Defourneau, D. & Klein, J. Spatial and energy variation of the local density of states in the charge density wave phase of 2H–NbSe2. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 14, 1070 (1996).
Mallet, P. et al. Contrast reversal of the charge density wave STM image in purple potassium molybdenum bronze K0.9Mo6O17. Phys. Rev. B 60, 2122–2126 (1999).
Tan, H. & Yan, B. Abundant Lattice Instability in Kagome Metal ScV6Sn6. Phys. Rev. Lett. 130, 266402 (2023).
Korshunov, A. et al. Softening of a flat phonon mode in the kagome ScV6Sn6. Nat. Commun. 14, 6646 (2023).
Pokharel, G. et al. Frustrated charge order and cooperative distortions in ScV6Sn6. Phys. Rev. Mater. 7, 104201 (2023).
Li, H. et al. Electronic nematicity without charge density waves in titanium-based kagome metal. Nat. Phys. 19, 1591–1598 (2023).
Yang, H. et al. Superconductivity and orbital-selective nematic order in a new titanium-based kagome metal CsTi3Bi5. Preprtint at: https://doi.org/10.48550/arXiv.2211.12264 (2022).
Arguello, C. J. et al. Visualizing the charge density wave transition in NbSeF in real space. Phys. Rev. B 89, 235115 (2014).
Spera, M. et al. Insight into the charge density wave gap from contrast inversion in topographic STM images. Phys. Rev. Lett. 125, 267603 (2020).
Wen, J., Rüegg, A., Wang, C.-C. J. & Fiete, G. A. Interaction-driven topological insulators on the kagome and the decorated honeycomb lattices. Phys. Rev. B 82, 075125 (2010).
Ferrari, F., Becca, F. & Valentí, R. Charge density waves in kagome-lattice extended Hubbard models at the van Hove filling. Phys. Rev. B 106, L081107 (2022).
Bradley, O., Cohen-Stead, B., Johnston, S., Barros, K. & Scalettar, R. T. Charge order in the kagome lattice Holstein model: a hybrid Monte Carlo study. npj Quantum Mater. 8, 21 (2023).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blaha, P. et al. WIEN2k: An Augmented Plane Wave plus Local Orbitals Program for Calculating Crystal Properties. (Vienna University of Technology, 2018).
Acknowledgements
I.Z. gratefully acknowledges the support from NSF-DMR 2216080 for STM measurements. Work at Rice is supported by the U.S. Department of Energy (DOE) grant No. DE‐SC0021421 (M.Y.), the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant no. GBMF9470 (M.Y.), and the Robert A. Welch Foundation grant no. C-2175 (MY). Z.R. acknowledges partial support by the Rice University Academy of Fellows program. S.D.W. and G.P. gratefully acknowledge support via the UC Santa Barbara NSF Quantum Foundry funded via the Q-AMASE-i program under award DMR-1906325. Material synthesis at University of Washington (UW) is supported by the Air Force Office of Scientific Research under Grant No. FA9550-21-1-0068 and the David and Lucile Packard Foundation. Work at the University of California, Berkeley and Lawrence Berkeley National Laboratory was funded by the U.S. DOE, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05CH11231 (Quantum Materials Program KC2202). This material is based in part upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-2140004. Part of the research described in this work was performed at the Canadian Light Source, a national research facility of the University of Saskatchewan, which is supported by Canada Foundation for Innovation (CFI), the Natural Sciences and Engineering Research Council of Canada (NSERC), the National Research Council (NRC), the Canadian Institutes of Health Research (CIHR), the Government of Saskatchewan, and the University of Saskatchewan. This research also used resources of the Stanford Synchrotron Radiation Lightsource, a U.S. DOE Office of Science User Facility under contract No. AC02-76SF00515. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. Z.W. acknowledges the support of U.S. Department of Energy, Basic Energy Sciences Grant No. DE-FG02-99ER45747 and the Cottrell SEED Award No. 27856 from Research Corporation for Science Advancement. B.Y. acknowledges the financial support by the European Research Council (ERC Consolidator Grant “NonlinearTopo”, No. 815869) and the ISF - Personal Research Grant (No. 2932/21). J.K. acknowledges support from the Robert A. Welch Foundation (through Grant No. C-1509). Work at Ames Laboratory is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, and Early Career Research Program. Ames Laboratory is operated for the US Department of Energy by Iowa State University under Contract No. DE-AC02-07CH11358.
Author information
Authors and Affiliations
Contributions
S.C. and H.L. carried out the STM experiments and analyzed the data under the guidance of I.Z. Z.R., J.S.O., Y.G., Y.Z. and Z.Y. carried out the ARPES experiments and analyzed the data with the help from S.G., M.Z., M.H. and D.L. under the guidance of M.Y. DFT calculations were performed by H.T., Y.L., L.K. and B.Y. Single crystals samples were synthesized by G.P. under the guidance of S.D.W., and J.M.D., E.R. under the guidance of J.-H.C. Z.W. provided theoretical input on the interpretation of the data. I.Z., Z.R. and M.Y. wrote the manuscript with input from all the authors. I.Z. and M.Y. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cheng, S., Ren, Z., Li, H. et al. Nanoscale visualization and spectral fingerprints of the charge order in ScV6Sn6 distinct from other kagome metals. npj Quantum Mater. 9, 14 (2024). https://doi.org/10.1038/s41535-024-00623-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-024-00623-9
This article is cited by
-
Orbital selective commensurate modulations of the local density of states in ScV6Sn6 probed by nuclear spins
Nature Communications (2024)
-
Spin Berry curvature-enhanced orbital Zeeman effect in a kagome metal
Nature Physics (2024)
-
Low-energy electronic structure in the unconventional charge-ordered state of ScV6Sn6
Nature Communications (2024)
-
Perspective: imaging atomic step geometry to determine surface terminations of kagome materials and beyond
Quantum Frontiers (2024)
-
Van Hove annihilation and nematic instability on a kagome lattice
Nature Materials (2024)