Introduction

One major development in contemporary physics is the discovery of Dirac and Weyl fermions emerging as low-energy quasiparticles in topological materials, which are accompanied by the quantum-mechanical geometric phases. Accordingly, the topological materials lead to various transport phenomena described by Berry phase theory1,2, which often show the marked enhancement of them and, in certain conditions, exhibit the quantized effect characterized by the universal constant, as exemplified by the anomalous Hall effect (AHE)3,4,5,6,7. In addition to such the transport phenomena at DC limit, the low-energy optical responses, which reflect the optical transitions among the topological bands near the Fermi level, also attract growing interest8,9,10,11,12,13,14,15,16,17. It has recently been recognized that the nonlinear optical effect and magneto-optical (MO) effect are enhanced in topological materials. Moreover, the spectroscopic research of such optical effects can give information on topological electronic structure along the energy axis that cannot be obtained from the transport property alone. The two-dimensional Dirac system provides a representative example of such topological electrodynamics. The mass gap at the Dirac point is induced by breaking of time-reversal symmetry through the spin-orbit interaction, resulting in the massive Dirac fermion. When the Fermi level is controlled in between the mass gap, the anomalous Hall response shows the quantized conductance e2/h, establishing the quantum anomalous Hall (QAH) state5,6,7. Correspondingly, the MO effects, which are the optical analogue of Hall effect12,13,14,15,16,17, also show the quantized optical rotation when the photon energy is well below the mass gap13,14,16. The quantized MO Faraday and Kerr rotations have been indeed demonstrated in the terahertz region in the magnetically doped topological insulators14,16. These quantized optical rotations, which emerge as off-resonant in-gap response of the massive Dirac band, can be viewed as the low-energy tail of the interband transition traversing the Dirac node for the higher photon energy exceeding the mass gap; the resonant enhancement of MO responses is expected to appear on the interband transition, showing the universal spectral shape described by a few parameters characterizing the massive Dirac band13. Although this MO transition is the essential origin of the quantized electrodynamics, the resonance itself has yet to be observed experimentally.

Recent extensive materials research has revealed massive Dirac bands in many systems other than the doped material, which could exhibit the high-temperature QAH effect6,7,18,19,20,21,22,23,24. Thanks to the special lattice geometry, the kagome-lattice magnets have been found to commonly host the massive Dirac bands at K and K’ points of the Brillouin zone18,19,20,21,22,23,24, as expected from the tight-binding model considering the spin-orbit coupling (Fig. 1a; see also Supplementary Note 1)25,26. This Dirac fermion is strongly coupled to the long-range magnetic orders. Therefore, the kagome-lattice magnets can realize the intrinsic QAH state without magnetic dopants, providing the ideal platform for its high-temperature realization and exploration of intriguing electromagnetic responses and functionalities27,28,29,30,31,32.

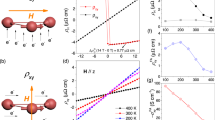
Fig. 1: Electronic structure and optical properties of topological kagome magnet TbMn6Sn6.
figure 1

a Schematic illustration of the massive Dirac fermions arising from the kagome lattice with the out-of-plane magnetic moment. b Crystal structure of TbMn6Sn6. The Tb and Mn spins are ferrimagnetically ordered as indicated by red and blue arrows. c The kagome network formed by the Mn atoms (upper panel) and schematic of the Mn 3dxy orbital lying within ab plane (lower panel). The local coordinates for the xy orbital are indicated in the upper panel. d The DFT calculation. See Supplementary Fig. 2 for the definition of high-symmetry points in Brillouin zone. The color bar shown in the right side represents the weight of the Mn 3dxy orbital. The purple dotted curve highlights the massive Dirac band. The light blue arrow denotes the lowest-energy interband transition within the massive Dirac band, which causes the enhanced MO effects. e Temperature dependence of optical conductivity spectra in the kagome plane σxx(ω). f Temperature dependence of the Kerr rotation spectra θK(ω) for the kagome plane.

Full size image

Here, we report on the low-energy MO resonance derived mainly from massive Dirac fermions in the kagome-lattice magnet TbMn6Sn6. By combining the broadband MO spectroscopy and first-principles calculation, we reveal that the massive Dirac bands significantly contribute to the observed resonance structure in the optical Hall conductivity. The spectral analysis quantitatively elucidates the overall response function of massive Dirac fermions including their large contribution to the DC anomalous Hall response. The present result is closely related to the universal electrodynamics in the QAH state.

Results and discussion

Electronic structure and optical property of TbMn6Sn6

The kagome-lattice ferrimagnet TbMn6Sn6, the structure of which belongs to a space group P6/mmm22,23, has the Mn and Sn atomic layers stacked alternatively along the c axis (Fig. 1b). The Mn atoms form the kagome lattice made of corner-sharing triangles (Fig. 1c). Below the transition temperature of ~ 423 K, the Mn and Tb moments are ferrimagnetically ordered. In line with the tight-binding model, the density functional theory (DFT) calculation shows the existence of massive Dirac bands at K and K’ points with the Dirac node position around 120 meV above the Fermi level as highlighted by the purple dotted curve in Fig. 1d (for the details of band calculation, see Methods and Supplementary Fig. 2). The Dirac bands are composed mainly of the Mn 3dxy orbital lying within the ab plane (Fig. 1c, d), which forms two-dimensional network. In fact, the recent scanning tunneling microscopy (STM) measurement demonstrates the presence of quasi-two-dimensional Dirac electron in three-dimensional crystalline lattice based on the observations of the Landau level formation, quasiparticle scattering pattern, and side surface modes inside the mass gap22.

The single crystals of TbMn6Sn6 were prepared by using the Sn-flux method. Plate-like crystals with the flat surface of (0001) kagome planes was used for optical measurements (for more details, see Methods). Figure 1e shows the optical conductivity spectra in the kagome plane σxx(ω) deduced from the reflectivity measurement through the Kramers-Kronig (KK) analysis (for more details, see Methods and Supplementary Fig. 3)31,32. In accord with the good metallic behavior of the resistivity23 (Supplementary Fig. 4a), we observe the steep increase of σxx(ω) below 0.1 eV towards zero energy due to the Drude response (Supplementary Fig. 5). As the width of Drude peak is narrower at low temperatures, the clear dip structure appears at around 0.1 eV. Above this dip energy, the interband optical transition shows the nearly flat continuum-like spectra. Since the Dirac point is located at around 0.12 eV above the Fermi level, the vertical transitions within the massive Dirac bands are expected above 0.24 eV. The two-dimensional Dirac bands exhibit the universal optical conductance for such interband transitions33, which would correspond to the optical conductivity of ~ 679 Ω−1 cm−1 for the present quasi-two-dimensional bulk material (see also Supplementary Note 2 and Supplementary Fig. 6). This value, however, cannot account for the observed large optical conductivity ~ 2000 Ω−1 cm−1, indicating that the optical response σxx(ω) is dominated by the optical transitions between trivial bands.

Infrared MO spectroscopy

To explore the intrinsic electromagnetic phenomena of the kagome-derived Dirac fermions, we focus on the infrared MO response near the lowest energy vertical transition of Dirac dispersion around 0.3 eV (see the light blue arrow in Fig. 1d). Figure 1f shows the magneto-optical Kerr rotation spectra θK(ω) ranging from 0.09 to 1 eV for the kagome plane, where the clear resonance structure is observed even at room temperature (see also Supplementary Fig. 7 and Methods). With decreasing the temperature, the resonance structure is enlarged and its peak energy shifts towards the higher-energy region. The additional small dip structure grows up around 0.12 eV.

The complex optical Hall conductivity spectra σxy(ω) are obtained from the σxx(ω) and magneto-optical spectra, enabling the comparison with the first-principles calculation as well as with the DC anomalous Hall conductivity (AHC) (Fig. 2a, b; see Methods for the derivation of σxy(ω)). Note that the spectral features of σxy(ω) are dominated by the Kerr rotation and ellipticity spectra and a high-energy extrapolation function used in Kramers-Kronig analysis for σxx(ω) hardly affects the following discussions and conclusion (see Supplementary Note 4). In general, the imaginary part of σxy(ω), Im σxy(ω), expresses the presence of optical transitions for the circularly polarized light; the integral of the spectral weight of Im σxy(ω) gives the DC AHC owing to the sum-rule of spectral weight17,34. On the other hand, the real part of σxy(ω), Re σxy(ω), shows the dispersive structure on the resonance in addition to the off-resonant contributions from higher-lying resonances, and Re σxy(ω = 0) is observed by the transport Hall measurement.

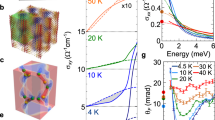
Fig. 2: Experimental and theoretical optical Hall conductivity spectra.
figure 2

a, d The experimental optical Hall conductivity spectra σxy(ω) at 8 K (a) and DFT calculation (d). The red and blue curves represent the real and imaginary parts of σxy(ω), respectively. b, c The temperature dependence of the real (b) and imaginary (c) parts of the optical Hall conductivity spectra. The black solid curves represent the spectra measured at 8, 30, 50, 100, 150, 200, 250, and 300 K. The color bar shown in the right side represents the magnitude of the optical Hall conductivity.

Full size image

The observed spectra have the prominent peak around 0.4 eV in Im σxy(ω) and the dispersive structure in Re σxy(ω) at 8 K (Fig. 2a), indicating the emergence of strong MO transition. The peak height ( ~ 160 Ω−1cm−1) is comparable with the DC AHC of ~ 200 Ω−1cm−1 (Supplementary Fig. 4b and c), manifesting that this resonance plays the dominant role for the DC anomalous Hall response, as we quantitatively evaluate later. This Hall resonance around 0.4 eV robustly remains at higher temperatures with slight spectral changes (Fig. 2b and c). In addition to the main peak mentioned above, the small resonance structure is observed below 0.2 eV in Im σxy(ω), which corresponds to the increase of Re σxy(ω) around the low-energy edge of present experimental window ( ~ 0.09 eV) through the KK relation. It should be emphasized that the clear resonance structure is observed only in the optical Hall conductivity σxy(ω), while the longitudinal optical conductivity σxx(ω) shows the rather flat continuum beside the low-energy Drude response (Fig. 1e).

The DFT calculation (Fig. 1d), which well reproduces the experimentally observed massive Dirac bands in terms of Dirac node position, mass gap and Fermi velocity22, allows us to examine the electromagnetic responses of Dirac band. The overall spectral characteristics of the experimental σxy(ω) spectra, i.e., the resonance around 0.4 eV and low-energy increase below 0.15 eV, are qualitatively reproduced (Fig. 2a and d). The lower edge of vertical transition within the massive Dirac band is estimated to be 0.24 eV (see the light blue arrow in Fig. 1d), which coincides with the lower edge of the resonant peak in Im σxy(ω) for both the experiment and calculation. We also calculate the σxy(ω) spectra when the initial and final states of the optical transition are restricted only to the Mn 3dxy orbital, which makes up the massive Dirac band (see Supplementary Fig. 8). We find a marked resonance peak at 0.4 eV even in this restricted σxy(ω) similar to the experimental spectra despite the tiny portion of the joint density of states (JDOS) for the Mn 3dxy orbital with respect to the total JDOS. These results demonstrate that the interband transition between the massive Dirac bands significantly contributes to the pronounced resonance around 0.4 eV. Note that some differences are observed between the experiment and DFT calculation (Fig. 2a, d); for example, in Re σxy(ω), the sign change is not observed and the low-energy increase below 0.15 eV is more pronounced in the calculation. These discrepancies may be ascribed to the magneto-optical response arising from many trivial bands as shown in the band structure and in JDOS (Supplementary Figs. 2 and 8).

We also examine the σxy(ω) spectra for the different Dirac node position by changing the exchange splitting in the DFT calculation (Supplementary Fig. 9; see also Methods). We find the clear shift of resonance, which is well consistent with the Dirac node position, further supporting the present interpretation. We emphasize that the σxy(ω) strongly reflects the topological electronic structure that causes the large AHE resulting from the intense Berry curvature, while the σxx(ω) is determined mainly by the joint density of states and tends to include contribution from any bands. Therefore, it is reasonable that the Dirac bands exhibit the pronounced magneto-optical response, whereas σxx(ω) is dominated by many other trivial bands.

Universal MO response of massive Dirac fermions

The intriguing aspect of Dirac electrons is that their response exhibits the universal behavior determined by only a few parameters11,13,33. Once the existence of massive Dirac electron is established, the appearance of MO resonance as well as large AHE are guaranteed by the band topology irrespective of the detail of system. In the following, the optical Hall response of massive Dirac fermion is evaluated by using the analytical formula13. The corresponding model Hamiltonian H(k) is given as,

$$H\left(k\right)=-\mu {\sigma }_{0}+\sum _{i=x,y,z}{h}_{i}\left(k\right){\sigma }_{i}\,\quad{\rm{with}}\,\left({h}_{x},{h}_{y},{h}_{z}\right)=\left({k}_{x},{k}_{y},m\right),$$
(1)

where σ0 and σi (i = x, y, z) are the identity and Pauli matrices, respectively, and μ is the chemical potential. The resultant Dirac dispersion has the mass gap of 2|m | (Fig. 3a). The optical Hall conductivity can be calculated with use of the general expression given by the Kubo formula;

$${\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)=i\sum _{n,m}\frac{f\left({\varepsilon }_{m}\right)-f\left({\varepsilon }_{n}\right)}{{\varepsilon }_{m}-{\varepsilon }_{n}}\frac{\left\langle m|{J}_{y}|n\right\rangle \left\langle n|{J}_{x}|m\right\rangle }{\hbar \omega +i\gamma +{\varepsilon }_{m}-{\varepsilon }_{n}},$$
(2)

where the Jx(y) is the current operator given by \(\frac{\hslash }{e}\sum _{k}{c}^{\dagger }(k)\frac{\partial H\left(k\right)}{\partial {k}_{x\left(y\right)}}c(k)\), f(εn) is the Fermi distribution function, εn and |n〉 are the energy and the Bloch wave function of the n-th band, respectively, and γ is the phenomenological broadening factor. The optical Hall conductance at zero temperature for the single two-dimensional massive Dirac fermion \({\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)\) is eventually given by,

$${\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)=\frac{{e}^{2}}{2h}\frac{m}{{{\hslash }}\omega +i{\gamma }}\mathrm{ln}\left|\frac{-{{\hslash }}\omega -i{\gamma }+2\mu }{{{\hslash }}\omega +i{\gamma }+2\mu }\right|.$$
(3)
Fig. 3: Analytical model calculation of optical Hall conductivity for the massive Dirac fermion.
figure 3

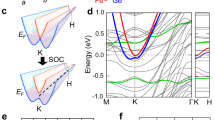
a The schematic illustration of the two-dimensional massive Dirac fermion assumed in the calculation. b The zero-temperature Hall conductance spectra arising from the single massive Dirac fermion; we adopted 2 m = 33 meV, μ = 113 meV, and γ = 22 meV. The purple filled area (∼ 2μ) denotes the optical gap. c Temperature variation of the calculated optical Hall conductance. In the right axes of (b) and (c), the two-dimensional optical Hall conductance \({\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)\) is extended into the three-dimensional optical Hall conductivity \(\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega \right)\) representing the responses of bulk materials. d Schematic illustration of the electronic distribution on the massive Dirac band at finite temperature.

Full size image

The vertical transition near the Dirac point causes the resonance peak at the energy of 2μ in Re σxy(ω), which corresponds to the lowest energy of the interband transition (red curve in Fig. 3b). The lower-lying tail of the resonance in Re σxy(ω) gives the DC AHC obtained by the transport measurement. On the other hand, Im σxy(ω) shows the step-function-like increase at the peak energy of Re σxy(ω), i.e. 2μ, and gradually decreases in higher energy (blue curve in Fig. 3b).

The response function of actual bulk material can be described by using \({\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)\) as

$${\sigma }_{{xy}}\left(\omega \right)={\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)\times \frac{1}{c}\times 4+{\sigma }_{{xy}}^{{\rm{const}}.}=\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega \right)+{\sigma }_{{xy}}^{{\rm{const}}.}.$$
(4)

\({\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega \right)\) is extended to the Hall conductivity \(\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega \right)\) for the present quasi-two-dimensional massive Dirac bands in the bulk crystal; the degeneracy coming from the valley degree of freedom and two kagome layers in unit cell results in a factor of 4, and c is the lattice constant along the stacking direction (c axis). We note that the finite kz dispersion may cause the spectral broadening of resonance, which is effectively included in the broadening factor γ (Supplementary Note 3). The constant term σxyconst. represents the low-energy tail of higher-lying resonances located above the present energy window. This analytical formula quantitatively reproduces the resonance structure at the lowest temperature (8 K) as shown in Fig. 4a. The obtained band parameters from the best fits, mass gap (2 m = 33 meV) and chemical potential (μ = 113 meV), are in a quantitative agreement with the previous STM study (2 m = 34 meV, μ = 130 meV)22. These quantitative agreements further corroborate that this MO resonance in σxy(ω) is the generic electromagnetic response of the massive Dirac band.

Fig. 4: Robust anomalous Hall response of massive Dirac fermions.
figure 4

Comparison between the experiment (solid curves) and analytical model calculation (dotted curves) at 8 K (a), 100 K (b), 200 K (c), and 300 K (d). The red and blue curves are the real and imaginary parts of σxy(ω), respectively. The calculated spectra in a are obtained without finite temperature effects, resulting in the band parameters of massive Dirac fermion as 2 m = 33 meV, μ = 113 meV, and γ = 22 meV. The temperature effects are included in (b)–(d) with using these same band parameters. e Temperature dependence of the AHC arising from the massive Dirac fermions \({\sigma }_{{xy}}^{{\rm{MD}}}\left(\omega =0\right)\) (red circles) and total AHC obtained from the transport measurement (green squares). The error bar is estimated from the variance of the electrical noise.

Full size image

We also deduce the temperature variation of \(\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega \right)\) by explicitly taking into account the temperature in Fermi distribution function in Eq. (2) with using the same band parameters m, μ and γ obtained at 8 K (Fig. 3c). The finite temperature effect largely changes the lower energy part of the resonance spectra because of the smearing of Fermi edge with energy width of kBT (Fig. 3d). The broadening and red shift of the sharp peak at 0.2 eV in Re σxy(ω) are observed at higher temperature (Fig. 3c), resulting in the enhancement of the low-energy spectral weight. These calculated temperature changes of \(\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega ,{T}\right)\) reasonably reproduce the experimental spectral variation of the resonance (Fig. 4b–d).

On the basis of this analysis, the AHC at ω = 0 arising solely from the massive Dirac bands, i.e.\(\,\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega =0,{T}\right)\) (red circles in Fig. 4e), is evaluated, while the total DC AHC is composed of the sum of contribution from all the bands as well as from the extrinsic mechanism. \(\widetilde{{\sigma }_{{xy}}^{{\rm{MD}}}}\left(\omega =0,{T}\right)\) accounts for the dominant part of AHC in the present material (Fig. 4e) and slightly increases with temperature due to the enhancement of low-energy spectral weight (see also ω = 0 in Fig. 3c). The massive Dirac bands give rise to almost 15 % of the quantized Hall conductance e2/h per each kagome layer, which persists even at room temperature. These results indicate that the electrodynamics of massive Dirac fermions derived from the defect-free kagome-lattice magnet is robust against the thermal agitation.

In summary, we have studied the infrared magneto-optical response of the kagome-lattice ferrimagnet TbMn6Sn6. Our experimental and theoretical spectroscopies demonstrate the anomalous Hall resonance arising mainly from the two-dimensional massive Dirac fermions. The spectral characteristics can be described by the analytical model with a few parameters characterizing the massive Dirac bands, establishing its general optical response directly connected to the large and robust AHE. In other words, both the presently observed magneto-optical resonance and the large DC AHE are the consequence of intense Berry curvature resulting from the massive Dirac fermion or of its band topology. These observations are also closely related to the universal electrodynamics of the QAH state with the quantized MO rotations in the terahertz region14,16, although the material response deviates from such the quantized limit in the present system because of the finite energy distance between Fermi level and Dirac point and of the coexistence of trivial bands. This is totally distinct from that of the conventional quantum Hall state supported by the Landau level formation35. The present findings are applicable to other massive Dirac fermion systems including recently developed kagome-lattice materials, and will be useful for the future terahertz and infrared magneto-optical applications.

Methods

Single crystal growth

Single crystalline samples of TbMn6Sn6 were prepared by using the Sn-flux method. An initial composition of Tb:Mn:Sn = 1:6:30 was sealed in an evacuated quartz tube. The ampoule was heated up to 900 °C and slowly cooled down to 500 °C for over six days, at which point excess flux was removed by centrifugation. Plate-like crystals with metallic luster were found, where the flat surfaces were confirmed to be the (0001) kagome planes by using Laue x-ray diffraction.

Transport measurement

The magneto-resistivity and Hall resistivity were measured by using Physical Property Measurement System (Quantum Design).

Optical conductivity σ xx(ω) and optical Hall conductivity σ xy(ω)

The optical conductivity spectra were deduced through the Kramers-Kronig transformation of the reflectivity spectra from 0.01 to 4 eV (Supplementary Fig. 3). We measured the reflectivity spectra using a Fourier-transform-type spectrometer in the infrared region (0.01–1 eV) and a mononchromator-type spectrometer in the visible and ultraviolet regions (1–4 eV). For the extrapolation of the reflectivity data, we assumed that the reflectivity is proportional to ω−4 above the highest energy. In addition, we confirmed that another extrapolation reflectivity, which includes the core level excitations, does not change our conclusion (Supplementary Note 4). The optical Hall conductivity spectra were calculated by using the following formula; σxy(ω) = −σxx(ω)εxx1/2(ω)(θK(ω)+iηK(ω)).

Magneto-optical Kerr effect (MOKE) measurement

Magneto-optical Kerr rotation spectra were measured with use of a Fourier-transform-type spectrometer for 0.09–1 eV and a mononchromator-type spectrometer for 1–2 eV in combination with a photoelastic modulator (PEM)36. The detection of synchronous signal of the reflected light with the fundamental and second harmonic of the modulation frequency enables us to measure the Kerr ellipticity ηK and rotation θK, respectively. For this measurement, we prepare the single domain state by the following procedures: Below 150 K, the M-H curve shows the clear hysteresis, which demonstrates that the single ferromagnetic state can be maintained at zero field (Supplementary Fig. 4d). Thus, we first applied the magnetic field of ±1 T to align the ferromagnetic moment and then switch off the field. On the other hand, since the hysteresis is not clear above 150 K, we applied the weak magnetic field of ±0.5 T to saturate the magnetization during the measurement. To deduce the MOKE spectra, we anti-symmetrized the spectra for the positive and negative magnetizations.

Density functional theory (DFT) calculation

The electronic structure of TbMn6Sn6 was calculated using Quantum ESPRESSO37, based on the crystal structure reported from neutron diffraction measurements38. We used full relativistic projector augmented-wave (PAW) pseudopotentials in the pslibrary39. For the exchange-correlation functional, the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation40 was employed. The cutoff energies for the wave function and the charge density were set to 50 Ry and 500 Ry, respectively. We performed calculations allowing spin polarization with the k-point mesh of \(7\times 7\times 5\). We assumed ferromagnetic spin configurations at Mn sites. The Tb 4 f electrons are assumed to be frozen in the core. Because the spin-polarized DFT often overestimates the magnetic exchange splitting, we put a penalty term to reduce the magnetization. With the penalty term, the energy level of the Dirac points becomes consistent with the previous STM result22.

Wannier representation and optical conductivities

From the Kohn–Sham Bloch states, a Wannier basis set was constructed using Wannier9041. The basis consists of d-character orbitals at Tb and Mn sites and (s, p)-character orbitals at Sn sites (59 orbitals per spin per formula unit). These sets were extracted from 164 bands in the energy window of −15 eV to +20 eV. We also employed the frozen window of −15 eV to 3 eV.

The optical Hall conductivity was calculated based on Kubo-Greenwood formula given by,

$${\sigma }_{\alpha \beta }\left({{\hslash }}\omega \right)=\frac{i{e}^{2}{{\hslash }}}{{N}_{{\bf{k}}}{\Omega }_{c}}\sum _{{\bf{k}},n,m}\frac{{f}_{m,{\bf{k}}}-{f}_{n,{\bf{k}}}}{{\varepsilon }_{m,{\bf{k}}}-{\varepsilon }_{n,{\bf{k}}}}\frac{\left\langle {\psi }_{n,{\bf{k}}}|{v}_{\alpha }|{\psi }_{m,{\bf{k}}}\right\rangle \left\langle {\psi }_{m,{\bf{k}}}|{v}_{\beta }|{\psi }_{n,{\bf{k}}}\right\rangle }{{\varepsilon }_{m,{\bf{k}}}-{\varepsilon }_{n,{\bf{k}}}-\left({{\hslash }}\omega +i{\eta }\right)},$$
(5)

where e, \(\hslash\), Ωc, Nk, η,\(\,{f}_{n,{\boldsymbol{k}}}\) are the elementary charge, reduced Planck constant, cell volume, number of k points, smearing parameter, and the Fermi-Dirac distribution function with the band index n and the wave vector k, respectively. The calculation was performed using the Wannier-interpolated band structure with a \(175\times 175\times 175\) k-point grid and η = 50 meV.

In Supplementary Fig. 8, we show the σxy(ω) when the initial and final states are restricted to the Mn 3dxy orbital. This orbital-resolved σxy(ω) can be calculated by the following formula;

$${\sigma }_{{xy}}\left({{\hslash }}\omega \right)=\frac{i{e}^{2}{{\hslash }}}{{N}_{{\bf{k}}}{\Omega }_{c}}\sum _{{\bf{k}},n,m}\frac{{f}_{m,{\bf{k}}}-{f}_{n,{\bf{k}}}}{{\varepsilon }_{m,{\bf{k}}}-{\varepsilon }_{n,{\bf{k}}}}\frac{{w}_{n,{\bf{k}}}{w}_{m,{\bf{k}}}\left\langle {\psi }_{n,{\bf{k}}}|{v}_{x}|{\psi }_{m,{\bf{k}}}\right\rangle \left\langle {\psi }_{m,{\bf{k}}}|{v}_{y}|{\psi }_{n,{\bf{k}}}\right\rangle }{{\varepsilon }_{m,{\bf{k}}}-{\varepsilon }_{n,{\bf{k}}}-\left({{\hslash }}\omega +i{\eta }\right)},$$
(6)

where wn,k represents the weight of the Mn 3dxy orbitals for n-th band shown in Fig. 1d. Here, the Bloch state |ψn,k〉 in the band basis is given by |ψn,k〉=∑α Uαn (k) |φα,k〉 with |φα,k〉 being the Bloch state in Wannier-orbital basis. As described above, we construct 118 Wannier orbitals (59 orbitals per spin). Out of 118 Wannier orbitals, we have 12 Mn 3dxy Wannier orbitals (note that there are six Mn atoms in the unit cell). Then, the weight of the Mn 3dxy orbitals for n-th band is given by \({w}_{n,{\bf{k}}}={\sum }_{\beta }{|{U}_{\beta n}\left({\bf{k}}\right)|}^{2}\), where the summation runs for 12 Mn 3dxy orbital indices.