CrRhAs: a member of a large family of metallic kagome antiferromagnets

Abstract

Kagome lattice materials are an important platform for highly frustrated magnetism as well as for a plethora of phenomena resulting from flat bands, Dirac cones and van Hove singularities in their electronic structures. We study the little known metallic magnet CrRhAs, which belongs to a vast family of materials that includes 3d, 4f, and 5f magnetic elements, as well as numerous nonmagnetic metals and insulators. Using noncollinear spin density functional calculations (mostly spin spirals), we extract a model magnetic Hamiltonian for CrRhAs. While it is dominated by an antiferromagnetic second nearest neighbor coupling in the kagome plane, the metallic nature of the compound leads to numerous nonzero longer range couplings and to important ring exchange terms. We analyze this Hamiltonian and find unusual ground states which are dominated by nearly isolated antiferromagnetic triangles that adopt 120^∘ order either with positive or with negative vector chirality. We discuss the connection to the few known experimental facts about CrRhAs. Finally, we give a brief survey of other interesting magnetic members of this family of kagome compounds.

Introduction

Due to strong geometric frustration, antiferromagnetism on a kagome lattice is expected to yield complex properties such as classical or quantum spin liquids^1,2,3,4. A good example with well-localized spin-1/2 copper magnetic moments forming a kagome lattice is herbertsmithite (ZnCu₃(OH)₆Cl₂) which has been drawing a lot of interest since it was first synthesized in 2005⁵. It has long been discussed as a quantum spin liquid candidate⁶ but some kind of structural disorder plays a significant role⁷. Other examples of kagome antiferromagnets which are proximate to or actually realize quantum spin liquids are kapellasite (ZnCu₃(OH)₆Cl₂)^8,9, Y-kapellasite (Y₃Cu₉(OH)₁₉Cl₈)^10,11, and Zn-barlowite (ZnCu₃(OH)₆FBr)^12,13.

Deviations from this “canonical” model have also been attracting a lot of attention lately. One line of inquiry has been along the search for nontrivial magnetic properties in kagome models with more complex interactions. Some examples include ideal kagome with reduced symmetry^11,14, breathing kagome forming magnetic trimers^15,16,17,18 (which can host electrons¹⁷ or spin-waves¹⁹ with flat dispersion due to trimerization, as well as semimetals, including Weyl^20,21). Yet another direction is introducing anisotropic interactions (like Dzyaloshinskii-Moriya) generating non-coplanar magnetic patterns with non-zero scalar chirality and topological transport^22,23, or combining spin-ice Ising terms with twisted kagome geometry²⁴. Of course, these are only a few examples from a potentially long list.

Interestingly, good metals with kagome and kagome-like geometries have only relatively recently been studied intensively. A typical example is the intermetallic T_mX_n kagome series (T = Mn, Fe, Co; X = Sn, Ge; m:n = 3:1, 3:2, 1:1) with different kagome plane stackings²⁵. Much effort has been put into studying their topological properties (Dirac fermions and flat bands)^25,26,27. Related kagome metals, such as YMn₆Sn₆, exhibit a nontrivial topological Hall effect^28,29,30, while another kagome metal family, AV₃Sb₅ (A=K,Na,Cs), demonstrates a series of intriguing orders, including superconductivity^31,32,33,34. Importantly, kagome planes in these systems are not magnetically frustrated, but they retain interesting electronic properties due to the special features of the kagome dispersion: Dirac points, van Hove singularities, and flat bands. Kagome metals with antiferromagnetic frustration have been little studied so far^35,36.

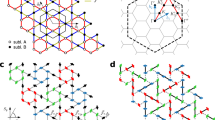
Ideal kagome lattices are not uncommon, but relatively rare. An important point in this regard is that most unique properties of kagome magnets do not, actually, require an ideal kagome geometry, but rather an ideal kagome connectivity. In this respect, there is no difference at the nearest neighbor level between a perfect kagome lattice and the one twisted by triangle rotations, as shown in Fig. 1. In this paper, we discuss a large family of compounds with the chemical formula XYZ and space group $P\bar{6}2m$ (no. 189). Typically, they include two metal layers, X and Y with ligands Z integrated into the two layers at a ratio 1:2. Thus, the structure can be understood as a stacking of X₃Z at z = 0.5 and of Y₃Z₂ at z = 0. Due to two 6-fold rotoinversion axes, the metal planes can be described as twisted kagome, where ligands sit in high-symmetry positions inside the metal planes. One metal sublattice, as discussed below, is only moderately deformed from the ideal kagome, while the other, incorporating two ligand atoms per unit cell, has metals combined into trimers. The former subsystem is often magnetic, the latter usually not.

Fig. 1: Kagome lattice distortions within $P\bar{6}2m$ space group.

a Two 6-fold rotoinversion axes in the unit cell of the $P\bar{6}2m\,XYZ$ compound (center). x is the fractional coordinate of the X atom indicated by an arrow. The left panel shows red atoms forming a kagome sublattice which is twisted by triangle rotations. The right panel shows blue atoms forming triangles. b The type of sublattice is uniquely determined by v = x − 1/2. When v = 0, the sublattice is exact kagome; When ∣v∣ < 1/6, it is a twisted kagome; when ∣v∣ > 1/6 it is trimers. The VESTA visualization program⁵² was used to generate this figure.

The elemental base for this crystallographic family, known by its prototype ZrNiAl, where X = Zr, Y = Al, and Z = Ni, is large, and metallic layers can be formed by transition metals, lanthanides, actinides, alkaline earths, etc. Many of the compounds are magnetic, when X forms the magnetic sublattice, and the resulting frustration is identical to the ideal kagome model. A known but little studied representative of this family is CrRhAs^37,38,39,40. We have chosen it as an example to perform an extensive study of in-plane and out-of-plane magnetic interactions, using density functional theory (DFT) calculations. We use the energies of spin spirals to extract the important parameters of a Heisenberg plus ring exchange Hamiltonian. We find that the second inplane exchange interaction clearly dominates over the first, leading to a spiral magnetic ground state. The dominant second-neighbor coupling is an interesting finding and shows that the twisted kagome lattice realized in CrRhAs and the entire family defined by its space group has remarkable properties beyond the known isotropic or distorted kagome lattice materials.

Results

X Y Z compounds with $P\bar{6}2m$ structure

In XYZ with $P\bar{6}2m$ space group, both X and Y sublattices are each characterized by one distortion parameter $v=x-\frac{1}{2}$, where x is the coordinate of the 3g (3f) Wyckoff position. The 3g and 3f positions differ only in the z coordinate, 1/2 and 0, respectively. The Z ions occupy two sublattices, 1b in the 3g plane, and 2c in the 3f plane. Increasing the absolute value of the distortion parameter ∣v∣ makes the equilateral X triangles grow and rotate in the X₃Z plane. This takes the X sublattice from an ideal kagome lattice at v = 0 via a kagome lattice with rotated triangles and deformed hexagons for $0 < | v| < \frac{1}{6}$ and a perfect triangular lattice at $| v| =\frac{1}{6}$ to trimers for $| v| > \frac{1}{6}$. At increasing ∣v∣, the triangular lattice of Z at the 1b position is enclosed by ever smaller X triangles. The v parameter has the same effect in the Y₃Z₂ plane with the difference that here, the Z in the 2c position form a honeycomb lattice. Thus, the connectivity in the two metal sublattices, X and Y, is different, which dramatically affects their magnetic properties. The compact triangles in the Y₃Z₂ plane tend to have considerable covalent bonding, and no, or little magnetism. The X ions, in contrast, form only a moderately twisted kagome lattice (minimizing the Coulomb interaction with the ligand in the center), and are likely to have magnetism which can be frustrated in case of antiferromagnetic interactions.

We have inspected the $P\bar{6}2m\,XYZ$ compounds on the materials project website⁴¹ and organized some potentially magnetic ones into convenient tables, shown in Supplementary Note 1, Supplementary Tables 1 to 3. We found a number of XYZ compounds with significant magnetism, where magnetic kagome atoms can be Ce, Cr, Eu, Ho, Dy, Fe, Gd, Mn, Np, Pu, or U.

CrRhAs

We used a projector augmented wave basis as implemented in the Vienna ab initio simulation package (VASP)^42,43,44 to perform noncollinear magnetic calculations—when needed, with individual constraints. We use all electron calculations with the full potential local orbital (FPLO) basis⁴⁵ to plot band structure and Fermi surface. The generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof variant (PBE)⁴⁶ was used as the exchange-correlation potential.

We base our calculations on the crystal structure of CrRhAs determined by Deyris et al.⁴⁷ (ICSD 43919) with a = b = 6.384(1) Å and c = 3.718(1) Å. The internal atomic positions of CrRhAs were relaxed in VASP while keeping lattice parameters fixed. The optimized structural parameters are shown in Table 1, and will be used from now on.

Table 1 GGA optimized fractional coordinates of CrRhAs.

Magnetic pattern analysis

In the following, we will infer magnetic couplings between Cr atoms (as shown in Fig. 2a) based on energies of different magnetic patterns on the Cr sublattices. In Fig. 2b, we define the three sublattices Cr1, Cr2, Cr3 of the kagome lattice. Arrows of different colors indicate the 1st to 4th in-plane nearest neighbor Cr atoms to a reference Cr1 atom. Each arrow associated with a Heisenberg term J_ns_i ⋅ s_j where J_n means nth in-plane nearest Heisenberg coupling and s_i=1,2,3 are normalized spin operators for Cr1, Cr2, Cr3. The polar angles of moments are assumed to be ϕ(1), ϕ(2), ϕ(3) for Cr1, Cr2, and Cr3, respectively. Figure 2a illustrates the connectivity of the J_n networks, with the same color convention as in Fig. 2b.

Fig. 2: Exchange paths and sublattice connectivity for CrRhAs.

a Twisted kagome lattice formed by Cr in CrRhAs, with 1st to 4th in-plane nearest neighbor exchange interaction marked by different colors. The unit cell contains three symmetry equivalent Cr, which we denote Cr1, Cr2, and Cr3. b Noncollinear and spiral calculations are set up focusing on Cr1, Cr2, and Cr3 (red, green and blue) sublattices. Connectivity is highlighted for the Cr1 sublattice. The dashed lines cut the lattice into stripes corresponding to different spiral angles.

We will discuss spin spirals propagating along different directions and with six cases of spin configurations within a unit cell defined as 120, FM, FI, (0,60,90), (0,45,120), (0,72,135) as shown in Fig. 3a. The ϕ(1), ϕ(2), ϕ(3) for each case are listed in Table 2. Besides, we also discuss periodic magnetic patterns with varying angle α as defined in Fig. 3b.

Fig. 3: Spin configurations for spirals and noncollinear calculations.

a Six spin configurations within a unit cell considered in spin spiral calculations. Red, green, and blue arrows indicate the moment directions of Cr1, Cr2, and Cr3, respectively. b Spin configurations of noncollinear ++α and +−α. Red, green, and blue vector are spin moments of Cr1, Cr2, and Cr3 sublattice respectively.

Table 2 ϕ(1), ϕ(2), ϕ(3) (in degrees) for the six different spin spirals.

The total energy of a magnetic pattern on Cr sublattices can be written as

$$H={E}_{0}+{H}_{{{{\rm{Heisenberg}}}}}+{H}_{{{{\rm{ring}}}}}$$

(1)

where H_Heisenberg is defined as

$${H}_{{{{\rm{Heisenberg}}}}}=\mathop{\sum}\limits_{i < j}{J}_{ij}{{{{\bf{s}}}}}_{i}\cdot {{{{\bf{s}}}}}_{j}$$

(2)

Here, the ${{{{\bf{s}}}}}_{i}=\frac{1}{S}{{{{\bf{S}}}}}_{i}$ are magnetic moment vectors normalized to 1. We write the exchanges in the kagome plane as J_ij = J₁, J₂, … where 1, 2, … correspond to increasing bond length (i.e., coordination shell). Exchange between the kagome layer and the next layer above and below are ${J}_{ij}={J}_{0}^{{\prime} },{J}_{1}^{{\prime} },{J}_{2}^{{\prime} },\ldots \,$, again sorted by distance (${J}_{0}^{{\prime} }$ is straight up or down). ${J}_{ij}={J}_{0}^{{\prime\prime} },{J}_{1}^{{\prime\prime} },{J}_{2}^{{\prime\prime} },\ldots \,$ are bonds connecting second layers, and so on. The identification of all bonds by Cr–Cr distance is provided in Supplementary Note 2.

H_ring is the ring exchange on a Cr triangle defined as

$${H}_{{{{\rm{ring}}}}}={L}_{1}\mathop{\sum}\limits_{{\bigtriangleup }_{1}}{{{{\bf{s}}}}}_{i}\cdot {{{{\bf{s}}}}}_{j}+{L}_{2}\mathop{\sum}\limits_{{\bigtriangleup }_{2}}{{{{\bf{s}}}}}_{i}\cdot {{{{\bf{s}}}}}_{j}$$

(3)

where

$$\mathop{\sum}\limits_{{\bigtriangleup }_{1}{\rm{or}}{\bigtriangleup }_{2}}=({{{{\bf{s}}}}}_{1}\cdot {{{{\bf{s}}}}}_{2})({{{{\bf{s}}}}}_{2}\cdot {{{{\bf{s}}}}}_{3})+({{{{\bf{s}}}}}_{1}\cdot {{{{\bf{s}}}}}_{3})({{{{\bf{s}}}}}_{3}\cdot {{{{\bf{s}}}}}_{2})+({{{{\bf{s}}}}}_{2}\cdot {{{{\bf{s}}}}}_{1})({{{{\bf{s}}}}}_{1}\cdot {{{{\bf{s}}}}}_{3})$$

(4)

Here, summation over Δ₁ or Δ₂ means that s_i=1,2,3 are the three moments of Cr1, Cr2, Cr3 that form 1st or 2nd nearest neighbor Cr triangle (red or blue triangles in Fig. 2a, respectively). L₁ and L₂ are the corresponding triangle ring exchange strengths.

With the above definitions, we can rewrite the total energy in Eq. (5) as

$$E={E}_{0}+{L}_{1}{D}_{1}+{L}_{2}{D}_{2}+\left(\mathop{\sum}\limits_{i}{J}_{i}{C}_{i}+\mathop{\sum}\limits_{i}{{J}_{i}}^{{\prime} }{{C}_{i}}^{{\prime} }+\cdots \,\right)$$

(5)

where ${C}_{i},{C}_{i}^{{\prime} },{D}_{1},{D}_{2}$ are summations of terms like s_i ⋅ s_j and (s_i ⋅ s_j)(s_j ⋅ s_k) that depend on magnetic patterns.

Spin spiral configurations

Spin spirals were modeled using the generalized Bloch theorem⁴⁸, as implemented in VASP. We calculated various spin spiral configurations for CrRhAs in order to get consistent information about the magnetic coupling between Cr ions in CrRhAs. A spin spiral is determined by a propagation vector q within the first Brillouin zone of the reciprocal space lattice. We mainly considered (q_x, 0, 0) and (0, 0, q_z) spirals.

The (q_x, 0, 0) spirals are propagating along the reciprocal b₁ direction, which is shown in Fig. 2b. To understand the connectivity in these spirals, we can divide the lattice into stripes (dashed lines in Fig. 2b) running along the unit cell vector a₂, which is perpendicular to b₁. From one stripe to the next, all moments are rotated by the angle θ_x = q ⋅ a₁. There is an additional freedom of choosing Cr moment directions ϕ(1), ϕ(2), ϕ(3) within the unit cell, which generates different spin configurations. We considered six types of (q_x, 0, 0) spin spirals, labeled as (120)[q00], (FM)[q00], (FI)[q00], (0, 60, 90)[q00], (0, 45, 120)[q00], (0, 72, 135)[q00] and corresponding (0, 0, q_z) spirals labeled by replacing [q00] with [00q]. For (0, 0, q_z), a spiral propagates along the a₃ direction, which is much simpler. All moments in a horizontal plane have the same spiral angle, and in the next plane along the a₃ direction, they rotate by θ_z = q ⋅ a₃. Explaining the energetics of such spirals requires out of plane exchange couplings.

Simple, if tedious, calculation renders a Heisenberg Hamiltonian that is a linear form in J’s and L’s, with the coefficients C_i and D for general (q_x, 0, q_z) spin spirals, as shown in Supplementary Note 3. For each spiral of the 120, FI, and FM cases, we performed spiral total energy calculations from spiral angle 0 to π, because their energy is symmetric with respect to spiral angle π up to J₄. For the other cases, (0, 60, 90), (0, 45, 120), (0, 72, 135), we calculated the full spiral angle range 0 to 2π.

Noncollinear periodic calculations

We also consider simple periodic cases where the three Cr sublattices have three different noncollinear spin directions, as shown in Fig. 3b, and where we vary the angle α. Taking the spin direction of Cr1 as reference, in the ++α case the spin directions of Cr2 and Cr3 are rotated by the same angle +α, while in the +−α case, the spin direction of Cr2 and Cr3 are rotated by +α and −α, respectively. The energy versus α curves and their fittings to different orders of cosine are shown in Supplementary Note 4.

If the magnetic interaction is dominated by Heisenberg-type contributions, we would expect that a simple $\cos (\alpha )$ will fit the ++α curve well. As we can see from Supplementary Fig. 2, the fit is indeed not bad with $\cos (\alpha )$ only, but after adding $\cos (2\alpha )$ it becomes much better. For the +−α case, we would expect $\cos (\alpha )$ plus $\cos (2\alpha )$ will fit well. However, it turns out that fitting to the order of $\cos (2\alpha )$ still has a large discrepancy with the calculated energies, and by adding a $\cos (3\alpha )$ term, two curves immediately snap together. So it is clear that explaining the +−α curve needs the $\cos (3\alpha )$ term.

One probable explanation is that there is ring exchange between three Cr atoms. For the spins s₁, s₂, s₃ of Cr_i=1,2,3, a ring exchange interaction is proportional to $\left({{{{\bf{s}}}}}_{1}\cdot {{{{\bf{s}}}}}_{2}\right)\left({{{{\bf{s}}}}}_{2}\cdot {{{{\bf{s}}}}}_{3}\right)+\left({{{{\bf{s}}}}}_{1}\cdot {{{{\bf{s}}}}}_{3}\right)\left({{{{\bf{s}}}}}_{3}\cdot {{{{\bf{s}}}}}_{2}\right)+\left({{{{\bf{s}}}}}_{2}\cdot {{{{\bf{s}}}}}_{1}\right)\left({{{{\bf{s}}}}}_{1}\cdot {{{{\bf{s}}}}}_{3}\right)$. In the +−α case, this will introduce $\cos (\alpha )\cos (2\alpha )$ and $\cos {(\alpha )}^{2}$ terms, and $\cos (\alpha )\cos (2\alpha )$ is equivalent to $\frac{1}{2}\left(\cos (3\alpha )+\cos (\alpha )\right)$, so that $\cos (3\alpha )$ emerges as soon as we consider ring exchange. For the ++α case, the ring exchange term introduces additional $\cos {(\alpha )}^{2}$ contributions that also improves the fit.

Fitting all energy curves

Energies of six (q_x, 0, 0) spirals, three (0, 0, q_z) spirals, ++α and +−α are shown in Fig. 4. Note that we have intentionally shifted the curves of ++α and +−α up to align with (FM)[q00] and (FM)[00q] at θ = 0, because due to the internal realization of VASP, energies of noncollinear and spiral calculations have a constant shift. From Fig. 4 The 120[00q] with θ = π has the lowest energy. This means that the interlayer coupling is AFM, and moments on Cr atoms on the same triangle tend to form 120 degree angles with each other.

Fig. 4: Energies for spiral and noncollinear spin configurations as function of angle.

Energy curves of six (q, 0, 0) spirals, three (0, 0, q) spirals, ++α and +−α.

Now we have 9 spiral curves plus 2 noncollinear curves with variable angle as shown in Fig. 4, which can be fit to Eq. (5), using Supplementary Table 5. It appears that only a subset of J’s are linearly independent; furthermore, some longer-range couplings, while they can formally be extracted by the fit, come out very small and improve the fit only marginally. A choice of ${E}_{0},{J}_{1},{J}_{2},{J}_{3},{J}_{4},{J}_{0}^{{\prime} },{J}_{1}^{{\prime} },{J}_{0}^{{\prime\prime} },{J}_{1}^{{\prime\prime} },L$ as a physically meaningful Hamiltonian gives good overall fits as shown in Fig. 5.

Fig. 5: Heisenberg plus ring exchange Hamiltonian fit of spiral and noncollinear DFT energies.

Least square fit of six (q_x, 0, 0) spirals, three (0, 0, q_z) spirals, ++α and +−α to the Heisenberg Hamiltonian including four in-plane neighbors, two neighbors in the first and second interplanar interactions, and the nearest neighbor ring exchange, as discussed in the text. Blue symbols are calculated DFT energies. Red curves are the least squares fit with the parameters shown on the right.

From this fitting result, we found that J₂ is the dominant exchange interaction. It is an antiferromagnetic coupling, and interestingly it is 10 times larger than the second largest ferromagnetic exchange interaction J₁. What is more, J₃, J₄ are also of the same order of magnitude as J₁. The nearest and next nearest interlayer coupling is antiferromagnetic. Thus, we find a Heisenberg Hamiltonian with clearly dominating antiferromagnetic interactions, in agreement with the fact that experimentally CrRhAs was found to order antiferromagnetically with a Neel temperature of T_N = 165 K³⁷. Considering the hierarchy of exchange couplings, we expect the J₂ triangles to order in a 120 degree state. The second largest ferromagnetic J₁ couplings cannot be exactly satisfied because of J₁-J₂-J₁ triangles, and they already introduce some frustration. The smaller in-plane couplings J₃ and J₄ also contribute to frustration. Interestingly, even though the interlayer distances of CrRhAs are small, interlayer exchange is much smaller than in-plane exchange, and the material is magnetically rather two-dimensional.

Furthermore, the ring exchange term is indispensable for good fits of the DFT energies and is substantial at 12% of the dominant exchange interaction. Note that we can directly compare Heisenberg and ring exchange terms as we are using unit moments. As shown in Supplementary Fig. 3, without ring exchange, there are discrepancies between fitted and original data curves as large as 20 meV for (120)[q00] and (120)[00q] at θ = 0, and similarly for +−α.

Discussion of the emerging Hamiltonian

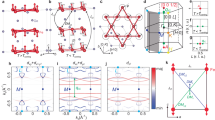
The Hamiltonian derived in the previous section is quite unusual. First, it is dominated by the large AF 2nd nearest-neighbor interaction (blue bonds shown in Fig. 2a). These bonds form isolated triangles, all oriented in the same way. Each triangle, obviously, orders in a 120^∘ fashion, and is formed by the three different Cr, Cr1, Cr2, and Cr3. Let us first for simplicity assume an XY model, so all spins lie in the ab plane (Fig. 7). There are two different ways to produce this order, illustrated in Fig. 6, differing by the sign of their vector chirality W = M₁ × M₂ + M₂ × M₃ + M₃ × M₁ on the dominant J₂ triangles. We use positive or negative vector chirality to distinguish between the two states (see Fig. 6). Toroidal moment ${{{\bf{T}}}}=\mathop{\sum }\nolimits_{i = 1}^{3}{{{{\bf{r}}}}}_{i}\times {{{{\bf{M}}}}}_{i}$ is usually non-zero for the state with positive vector chirality while it is always zero for the state with negative vector chirality. After one or the other type is selected, each blue triangle is fully determined by one of its spins (let’s say, by the Cr1 spin). Then the lattice of the blue triangles is equivalent to a triangular lattice shown in red (see Fig. 7).

Fig. 6: Toroial moment and vector chirality on a triangle of spins.

There are two topologically different 120^∘ magnetic patterns. Red, green, and blue vectors are spin moments of Cr1, Cr2, and Cr3 sublattices, respectively. Note that the left pattern (a) has an α dependent, usually non-zero toroidal moment $T=3\sin \alpha$ (assuming the black vectors r_i and magnetic moments have unit lengths), which can be continuously varied from 3 to −3 by rotating the spin space with respect to the coordinate space, while the right pattern (b) has always T = 0, and that is not affected by the spin-space rotation. The left pattern (a) has positive, the right pattern (b) negative vector chirality.

Let us now determine the effective Hamiltonian for this lattice: consider two blue triangles shifted along a. The Cr1 on the right is connected to Cr2${}^{{\prime}}$ and Cr3${}^{{\prime}}$ on the left, where “${}^{{\prime} }$” means the atoms from the left triangle. The corresponding contribution to energy is ${J}_{1}{{{{\bf{S}}}}}_{1}\cdot ({{{{\bf{S}}}}}_{2}^{{\prime} }+{{{{\bf{S}}}}}_{3}^{{\prime} })=-{J}_{1}{{{{\bf{S}}}}}_{1}\cdot {{{{\bf{S}}}}}_{1}^{{\prime} }$. Thus, the FM n.n. interaction gives rise to an AF interaction for this red bond, which needs to be added to the, also AF, J₃.

Let us now evaluate the interaction along a₂. By the same token, the coupling between the corresponding Cr2 atoms is also J_eff = J₃ − J₁. Since the moment of Cr2 is just the moment of Cr1 in the same gray triangle rotated by 2π/3, it is the same as adding J_eff along a₂ for the Cr1 atoms (note that in principle we could rotate spins in the opposite directions when shifting along a₂ compared to shifting along a₁, but that would have been energetically unfavorable).

Thus, we get a unique ground state, where the spins on the blue sublattice, which are of three different colors, form a 120^∘-lattice, and each color within itself also forms 120^∘-lattices. Next, let us look at the gray triangles. Their centers are denoted by green and orange dots. They form a perfect honeycomb lattice, but it partitions (as the honeycomb lattice is bipartite) into two (triangular again) subsets (green and orange), one sporting FM triangles and the other 120^∘-triangles. Note that in terms of the toroidal moments it is reversed: the former subset has zero toroidal moments, while the latter non-zero ones. Note that the J₄ interaction, comparable with J₃ (but considerably smaller than J_eff = J₃ − J₁) is also satisfied as well as it is possible for a triangular lattice, i.e., with 120^∘ angles.

If we now select the other pattern with a positive vector chirality on the dominant J₂ (blue) triangles, we end up with an alternative structure, strictly degenerate with the first one (Fig. 7b).

Fig. 7: Possible ground states for dominant Heisenberg interactions of CrRhAs.

Two possible 2D ground states of the reduced magnetic Hamiltonian including J₁ to J₄ interactions (note that the ground state is highly degenerate). The blue bonds indicate the strongest exchange coupling (AF) in the system (J₂), which generates 120^∘ trimers, the gray bonds the nearest neighbor triangles, and the red one effective inter-trimer AF interaction, numerically equivalent to J₃−J₁. Note that while in the ground state the blue trimers are ordered in a 120^∘ fashion, and the red bonds network also assumes a 120^∘ order, the two orders, in this model, are not correlated and may have different ordering planes and toroidal moments. The blue dots indicate centers of the blue trimers, and the green and orange ones centers of the n.n. triangles. The top diagram (a) corresponds to an order with negative vector chirality on the blue triangles, the bottom one (b) to one with positive vector chirality.

To summarize, the effective model can be mapped onto a triangular lattice where each site is characterized by a Heisenberg-spin variable (let us call it Σ, which shows the spin direction of the selected corner (Cr1, in this case), and another unit-length axial vector, Ω, showing the sense of the rotation in a given blue triangle (i.e., rotations from Cr1 to Cr2 to Cr3 by 2π/3 proceed around the axis Ω, and the sense of the rotation is given by the sign of Ω). The interaction between the effective spins Σ is also Heisenberg, AF, and much smaller than the interactions inside a trimer. Note that while magnetically the system partitions naturally into trimers, electronically it maintains full connectivity, so electronic flat bands arising in breathing kagome systems with a physical trimerization¹⁷ do not appear here. This leads to a standard triangular Heisenberg order, which can also be characterized by a Heisenberg spin variable, S₀, which can be selected as the value Σ₀ at the origin, and another unit-length rotation vector, ω. At the end, the entire long-range magnetic order can be described by one Heisenberg spin Σ₀ and two axial rotational vectors Ω and ω. This is to be contrasted with the less-degenerate standard triangular lattice, which can be uniquely described by the origin spin and one rotational vector.

Consideration of the second type of ordering, the one with positive vector chirality on the J₂ triangles, proceeds along the same lines. The results are summarized in Tables 3 and 4. The main difference is that in the former case half of the nearest neighbor triangles have non-zero toroidicity, which however averages to zero, while in the latter the same is true for the second-neighbor trimers.

Table 3 Toroidicity and chirality in the spin configuration with negative vector chirality on the dominant J₂ triangles, as discussed in the main text.

Table 4 Same as Table 3, for the spin configuration with positive vector chirality on the dominant J₂ triangle.

Adding the ring exchange which we found to be sizeable does not alter this ground state. Indeed, it is easy to show that if an AF coupling on a triangle J > 7L/2 the ground state is not altered by adding the ring exchange. Finally, interaction along the c axis is strongly frustrated, with comparable ${J}_{0}^{{\prime} },{J}_{1}^{{\prime} }$, and ${J}_{1}^{{\prime\prime} }$, which can lead, generally speaking, to spiral states propagating in this direction (given the higher coordination number for the last two).

While these two states have been discussed above in terms of supercells, one can notice that they also form spin spirals of a sort. Namely, the first one can be described, using our notations, as the (120, 0, 0)[4π/3, 4π/3, 0] spiral, and the second as the (0, 120, 120)[2π/3, 2π/3, 0] one. Note that in this Hamiltonian, the two spirals are degenerate, and have not been included in our previous calculations and fitting. Thus, these two states are true predictions and can be explicitly verified. Indeed, we found that, as predicted by the model Hamiltonian, they are (a) degenerate within computational accuracy and (b) 25.6 meV below the lowest-energy state found in the original calculations (namely, the standard 120^∘ structure alternating antiferromagnetically between the planes.)

The last observation relates to the situation that, when the ordering planes are not parallel, Ω∦ω, a finite local scalar chirality can be acquired, leading, for instance, to a topological Hall effect. This opens the door to a fluctuation-induced topological Hall effect at finite temperature²⁸; however, further analysis is outside the scope of this paper.

Comparison with experiment

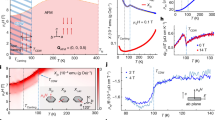
Experimental information on this material is, basically, limited to four papers from T. Kaneko and co-authors^37,38,39,40. It has been established that CrRhAs experiences an antiferromagnetic transition, with the Néel temperature reported at T_N = 165 K^37,38,39 or 172 K⁴⁰. The antiferromagnetic order has not been established. Interestingly, the magnetic susceptibility measured in an interval between T_N and room temperature is distinctly non-Curie-Weiss (CW). In the first publication, ref. ³⁷, it was fitted to the CW law, χ = C/(T − Θ) + const, but with a background of 1.47 × 10⁻³ emu/mole, which, if interpreted as Pauli susceptibility, corresponds to 45 states/(eV ⋅ f.u.), or to an ad hoc formula $\chi ={C}^{{\prime} }/{(T-{\Theta }^{{\prime} })}^{\gamma }$, with ${C}^{{\prime} }=4.8\times 1{0}^{-3}$ emu K/mole, ${\Theta }^{{\prime} }=20$ K and γ = 0.16. In a later paper, ref. ³⁸, the same formula was used with $\chi ={C}^{{\prime} }/{(T-{\Theta }^{{\prime} })}^{\gamma }$, with ${C}^{{\prime} }=3.2\times 1{0}^{-2}$ emu K/mole, ${\Theta }^{{\prime} }=-16$ K and γ = 0.44, presumably, due to a different protocol for the background removal. Either way, χ⁻¹(T) is strongly nonlinear and its slope gets smaller with the temperature. If one defines “instantaneous” CW parameters as C(T) = 1/(dχ⁻¹(T)/dT) and Θ(T) = T − C(T)/χ(T), then Θ(T) is becoming increasingly antiferromagnetic with temperature, and C(T) also grows, corresponding to increasingly large effective moments.

All these observation, as strange as they may seem on the first glance, find natural explanations in our Hamiltonian and proposed ground state. Indeed, the former is dominated by the very strong J₂ interaction, which itself corresponds to a temperature scale of 2J₂ (2 for the coordination number) of the order of 1000 K, or if converted to the CW temperature and assuming spin 3/2 and the quantum factor (S + 1)/S = 5/3, corresponds to T_CW = − 578 K. This indicates that at room temperature the isolated trimers formed by the J₂ bonds are still strongly correlated, forming complexes with strongly suppressed net magnetic moment. As a result, the true CW regime is not attained until T ≳ 600 K, and the observed behavior is nothing but a graduate crossover from the fully correlated trimers with the effective moment m_eff ≪ 1μ_B and T_CW defined by the other (besides J₂) interactions in the system (which is on the order of −72 K), and the very high-temperature regime, not reached in the reported experiments, where ${m}_{{{{\rm{eff}}}}} \sim \sqrt{3\cdot 5}=3.87\,{\mu }_{B}$, and T_CW ~ −650 K. Finally, the relatively small value of T_N compared to the high T_CW temperature finds a natural explanation in the fact that the intra-trimer ordering that does happen at high temperature is not related to the temperature at which the individual triangles order with respect to each other; the latter is determined by the much weaker inter-trimer interactions. In fact, an upper boundary on the mean-field transition temperature can be derived by taking all interactions but J₂ with the same sign (remember that, for instance, J₁ and J₃, although they are of the opposite signs, cooperate in the suggested ordering). This gives an estimate for the maximally possible ordering temperature of 346 K. The experimental number is right between the lower estimate of 72 K and this upper bound.

Electronic structure of CrRhAs

Finally, we turn our attention to the band structure and Fermi surface of CrRhAs. We use GGA calculations with the FPLO basis to determine both nonmagnetic (Fig. 8a) and examples of magnetic band structures (Fig. 8b, c). At the Fermi level, most of the density of states derives from Cr 3d, with only small Rh 4d and very small As 3p contributions (Fig. 8a). In the non-magnetic bands, a Dirac point at the K point can be seen about 0.4 eV above the Fermi level but flat bands are hard to make out. CrRhAs remains metallic in both ferromagnetic and ferrimagnetic states (Fig. 8b, c) as well as in antiferromagnetic spin configurations (not shown). However, DOS at E_F is substantially lower in magnetic compared to non-magnetic states. The non-magnetic Fermi surface (see Fig. 8d for cuts, Fig. 8h, i for 3D plots) has some cylinder-like 2D features but also significant variation along k_z. The FS for the ferromagnetic solution (Fig. 8e, f) is not much simpler.

Fig. 8: GGA electronic structure of CrRhAs.

a Nonmagnetic, b ferromagnetic, and c ferrimagnetic bands with corresponding densities of states. d k_x − k_y plane cuts of the Fermi surface for three different values of k_z. e, f The same for the ferromagnetic solution. g–j 3D contour plots of the nonmagnetic Fermi surface; g–i are three individual FS sheets, and j shows all of them together. In g–j, color indicates Fermi velocity where blue is low, orange high.

Discussion

We studied one member of a large family of XYZ compounds with space group $P\bar{6}2m$ that contains twisted kagome and trimerized (distorted triangular) lattices. As many as 70 of them have significant magnetism on a kagome lattice, and despite the distorted geometry, the magnetic interaction Hamiltonian remains the same as ideal kagome at the nearest neighbor level, which makes this series of compounds a fertile playground for kagome physics. We used CrRhAs as an example to study different spin spiral and noncollinear energies.

To this end, we have calculated within the density functional theory the total energies of six different in-plane spin spirals, three different out-of-plane spirals, and two continuously varying noncollinear magnetic arrangements with the q = 0 periodicity, a total of more than 230 first principle calculations. Based on these data, we generated a magnetic Hamiltonian that fits all these energies reasonably well (with max deviation within 15 meV). Interestingly, the resulting Hamiltonian was rather unusual in several aspects: first, we found that Heisenberg exchange interactions could not provide a satisfactory fit; adding ring exchange terms proved indispensable, especially for the two q = 0 sets of calculations. Second, we found that the nearest neighbor exchange coupling was ferromagnetic, and thus not frustrated, but the leading (by far) interaction was the next nearest neighbor antiferromagnetic coupling in the twisted kagome plane, which is frustrated and leads to a curious, and, to the best of our knowledge, never discussed before magnetic Hamiltonian. The ground state of this Hamiltonian is controlled by independent triangles of a certain vector spin chirality, either positive or negative, but the same for all triangles, and varying toroidicity between these triangles. Furthermore, it has a potential to develop, either statically due to spin-orbit coupling, or dynamically through topological field fluctuations, scalar spin chirality, and topological Hall effect. These possibilities, however, go beyond the scope of our paper.

We hope that this study would motivate further experimental and theoretical research into this intriguing family, and particularly this specific system. An unexpected outcome is that the twisted kagome lattice of XYZ compounds in $P\bar{6}2m$ space group with magnetic X can realize unusual highly frustrated Hamiltonians that are not known in pristine or distorted kagome materials and hold the promise of future discoveries and surprises.

Methods

Structure preparation

The structure relaxation and noncollinear magnetic calculations of CrRhAs were performed using the Vienna ab initio simulation package (VASP)^42,43,44. The projector augmented wave (PAW) potentials^49,50 with the generalized gradient approximation (GGA) exchange-correlation potential in the Perdew–Burke–Ernzerhof variant (PBE)⁴⁶ were used in all calculations. Explicitly, Cr_pv, Rh_pv, As_d potentials are used.

The internal atomic positions of CrRhAs were relaxed with lattice parameters a = b = 6.384(1) Å and c = 3.718(1) Å kept fixed based on the experimental structure by Deyris et al.⁴⁷ (ICSD 43919) using Γ-centered mesh 6 × 6 × 9 and energy cutoff 400 eV. The convergence criterion is that all forces are smaller than 0.01 eV/Å. The optimized structure was then used for noncollinear magnetic calculations.

Spin spiral calculations

Spin spirals were modeled using the generalized Bloch theorem⁴⁸, as implemented in VASP. The Γ-centered mesh was set to 8 × 8 × 12, and the lower and upper limits of the energy cutoff were set to 380 and 480 eV. The moments of Cr atoms are initially set to 4μ_B, and only the directions of the moments in the unit cell are constrained during the self-consistent process. With different moment configurations together with different spiral propagation vectors q, we calculated the total energies of different spin spirals of CrRhAs, and for each spin spiral, a corresponding Heisenberg Hamiltonian energy expression plus ring exchange terms involves different Js. By keeping a limited set of Js, we can obtain values for the exchange couplings and ring exchange via least squares fitting.

Electronic structure calculations

The band structures and Fermi surfaces were calculated using all-electron calculations with the full potential local orbital (FPLO) basis⁴⁵. As in VASP, GGA in the PBE variant was used as the exchange-correlation potential. Calculations are converged with a 24 × 24 × 24 k mesh. For the ferrimagnetic state, we lower the space group symmetry from P − 62m to Amm2. We use an extended basis set to increase the precision⁵¹. The spin-orbit coupling, expected to be small here, was not included in these calculations.