Abstract
The pairing mechanism of high-temperature superconductivity in cuprates is regarded as one of the most challenging issues in condensed matter physics. The core issue concerns how the Cooper pairs are formed. Here we report spin-resolved tunneling measurements on extremely underdoped Bi2Sr2−xLaxCuO6+δ. Our data reveal that, when holes are doped into the system, the antiferromagnetic order is destroyed, while at the same time an increasing density of states (DOS) peaked at around 200 meV appears within the charge transfer gap. Meanwhile, an electronic structure with 4a0 × 4a0 basic plaquettes emerges inhomogeneously, with an area fraction that grows with hole doping. In each plaquette, there are some unidirectional bars (along the Cu-O bond) which are most pronounced at energies near peaks in the DOS around at 25 meV, with an intensity that is especially pronounced at oxygen sites. We argue that the atomically resolved low-energy DOS and related gap are closely associated with some kinds of density waves, possibly reflecting modulations of the electron density, or a pair-density wave, i.e. a modulation of the local pairing. Our work sheds new light on the doping induced electronic evolution from the “parent” insulator of the cuprate superconductors.
Similar content being viewed by others
Introduction
According to the Bardeen-Cooper-Schrieffer (BCS) theory, superconductivity is induced by the condensation of Cooper pairs. In conventional superconductors, the Cooper pairing is established through exchanging phonons between two electrons with opposite momentum. The discovery that the superconducting order parameter in the high Tc cuprates has d-wave symmetry, along with its unprecedently high Tc presumably implies that a different mechanism is at play. Consequently, understanding the pairing mechanism in the cuprates has become one of the most interesting and challenging issues in condensed matter physics. Several theoretical models have been proposed in order to tackle this problem. An early scenario based on the resonating-valence-bond (RVB) state, envisaged spin-singlet pair formation induced by the antiferromagnetic (AF) superexchange interactions between local spins on the Cu ions1,2,3. Other magnetic pairing pictures invoke the exchange of AF spin fluctuations4,5,6. In the strong-coupling limit, the pairing could be very local, thus the picture concerning local pairing may provide an explanation for the high-Tc superconductivity. Of particular interest are the spatial inhomogeneity and the phase separation of electronic states, which can be induced by the frustrated quantum interactions in cuprates7,8, which could even lead to some forms of the local pairing in the hole-doped but non-superconducting cuprates. A picture concerning pair-density wave (PDW) of 2e particles was proposed9,10,11 in order to explain the real-space electronic modulations12 observed in scanning tunneling microscopy/spectroscopy (STM/S). Note that the meanings of the PDW in refs. 9,11 are different. The PDW state discussed in ref. 9 was argued to not only break the global gauge symmetry, but to have an order parameter that varies with position in such a way that its spatially average value vanishes, while the one described in ref. 11 referred to a modulated superconducting state coexisting with the charge density waves (CDW). Later, evidence of PDW order was discovered in the superconducting state of certain cuprates13,14, of a form that is more consistent with that proposed in ref. 9. In cuprates, although it is widely accepted that the high-Tc superconductivity is induced by doping holes or electrons into the AF Mott insulator, it remains unclear (i) how the “Mottness” is related to the destruction of the insulating gap and the vanishing of the long-range AF order, and (ii) what physics governs the emergence of the low-energy DOS, and what is the relationship between the corresponding excitations and superconductivity?
By using the spin-polarized (SP) STM/STS technique15,16, we report here a close relationship between the AF order and the Mottness derivative gap; meanwhile we show the emergence of low-energy DOS with a gapped feature around 25 meV within a 4a0 × 4a0 basic plaquette. We argue that these low-energy DOS features and the associated gap are probably induced by some kind of density wave, either of some form of local electronic gauge-invariant density, or a pair-density wave.
Results
Direct observation of the AF order
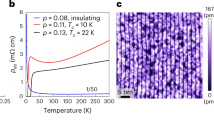
The Bi2Sr2−xLaxCuO6+δ (La-Bi2201) samples were grown with a traveling-solvent-floating-zone technique17. In our present studies, we use the samples with nominal compositions of x = 1 and 0.85 which correspond to hole doping levels of p = 0.08 and 0.10, respectively. For simplicity, we denote these samples as UD08 and UD10. The phase diagram of La-Bi2201 is shown in Fig. 1a, it is clear that the AF Mott insulating phase is almost vanished and the superconducting phase is just about to appear at the doping level of p = 0.1017,18,19.
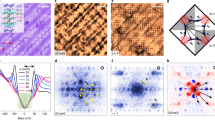
a Phase diagram of La-Bi2201 systems. The arrows indicate the doping levels of two samples studied here. b Temperature dependent resistivity measured in two extremely underdoped La-Bi2201 samples. c, d Spin-difference topographies derived by the subtraction of the topographic images measured by the Cr tip under magnetic fields with opposite directions in UD08 and UD10, respectively. The insets in (c) or (d) show the FT pattern of (c) or (d), and the dashed circles in inset of (c) indicate the pattern of the AF order observed in UD08.
The temperature dependent resistivity of these two samples shows clear insulating features (Fig. 1b), and UD08 exhibits a stronger insulating behavior than that of UD10. On some specimens taken from the same batch of UD10, we did see a tiny drop of resistivity at low temperatures, verifying that the doping is really at p = 0.10. We use the SP-STM to investigate the topographic images of these two kinds of samples (Supplementary Fig. 1) by using Cr tips polarized with magnetic fields along opposite directions15,16. After cleaving the sample in ultrahigh vacuum, the exposed surface is the Bi-O layer; in an ideal situation, the Bi atoms would locate at positions with the corresponding ones of Cu atoms in the Cu-O layer underneath20,21,22,23, but due to the super-modulation structure, they may have slight differences. Thus any magnetic moment detected by SP-STM should arise from the Cu-O layer. The spin-difference topographies of the samples are shown in Fig. 1c and d. The AF order can be clearly seen in some areas of UD08 (Fig. 1c), but it is almost invisible in UD10 (Fig. 1d). Such difference is clearer in the Fourier transformed (FT) patterns of the spin-difference topographies (insets of Fig. 1c, d), i.e., the AF order is clear and commensurate with the period of \(\sqrt 2 a_0\) along the diagonal direction of the lattice in UD08, but it is almost absent in UD10. We want to emphasize that, these AF related spots appear only in the FT spin-difference topographies of the UD08, they are absent in FT-topographies measured at zero or a finite field without the spin-difference treatment on the same sample (Supplementary Fig. 1), thus they are not induced by the structural distortion as in Bi221224.
Emergence of in-gap states in the regions with vanishing AF order
Next we investigate how the local AF order correlates with the Mottness derived gap through measuring the local spectrum. The AF order can be observed in some areas in UD08. Figure 2a shows the spin-difference topography measured in another area of UD08. The AF order is weak in the region surrounded by the dashed line. The differential conductance (dI/dV) mapping has been measured at 100 mV in the same region (Fig. 2b), and the local intensity in the mapping is roughly proportional to the local density of states (LDOS). One can see that the intensity of LDOS at 100 meV gets enhanced in the region with vanished AF order. In contrast, the LDOS is almost zero in the region with the AF order. In addition, in the region without the AF order, some patterns with dimensions of 4a0 × 4a0 emerge, and these newly emergent patterns are clearer in the inverse Fourier transform image (Fig. 2c, and supplementary Fig. 2) or measured with a low energy. The periodic patterns have been observed as checkerboard electronic modulations in underdoped superconducting cuprates25,26,27,28, and they are also observed in the vortex cores in optimally doped cuprate Bi2Sr2CaCu2O8+δ29. Therefore, the checkerboard electronic modulations may be closely related to superconductivity. Although our samples are highly insulating, we cannot exclude the possibility that these plaquettes originate from the nesting effect of Fermi surface in nanoscales30,31. Figure 2d shows a set of tunneling spectra measured along the arrowed line in Fig. 2a. In the region with an obvious AF order, the spectra are featureless showing a background within the Mottness derivative gap in a wide voltage range (up to about 1.5~2.0 V). In cuprates, it is known that the oxygen p-orbital hybridizes with the lower Hubbard band of Cu \(3d_{{{{\mathrm{x}}}}^2 - {{{\mathrm{y}}}}^2}\) orbital, leading to a charge transfer gap Δ in the scale of 1.5~2.0 V between the charge transfer band (CTB) and the upper Hubbard band (UHB)32. Despite the large charge transfer gap, but because there is a finite DOS in the negative energy side, the tunneling measurements can be successfully done with a set point of, for example, −400 mV for the dI/dV mapping and −1.0 V for the spectra. Here we must mention that, although our samples, especially the UD08, exhibit insulating behavior, the resistivity is still moderate, and it can be measurable in transport measurement down to 2 K, which manifests that the tip-induced band bending effect (TIBB)33 may exist, but not be strong in the present case. We didn’t see the impurity induced charging rings either34. In addition, the charge transfer gap obtained from our experimental data in UD08 is consistent with the widely expected values32. When the tip moves to the region with vanished AF order and the presence of the checkerboard modulations, one can see that the gapped energy range shrinks. In addition, the LDOS increases from both sides of Fermi level, and a hump-like feature of density of states appears on the spectra at about 150–200 mV. This is consistent with previous observations in the similar system in a very underdoped region35. In order to illustrate this emergent in-gap states more clearly, we take the first spectrum in the AF region as the background and subtract it from all other spectra, and show the data in Fig. 2e. One can see that the enhancement of DOS near the Fermi level is clearer in the narrow voltage range, showing a feature of the large pseudogap. Such features of suppressing the charge transfer gap and enhancing DOS near the Fermi level in underdoped samples have also been found by another group35. Here, for the first time, we illustrate directly that these features are closely related to the vanishing of the AF order, and this indeed verifies that the parent phase of cuprates is an antiferromagnetic Mott insulator.
a Spin-difference topography (Setpoint condition: Vset = −400 mV, and Iset = 50 pA). The AF order is weak in the region surrounded by the dashed line. b Differential conductance mapping measured in the same region of (a) (V = − 400 mV, I = 100 pA) at 0 T. The red squares indicate the obvious patterns of 4a0 × 4a0 appearing in the region with extremely weak AF order. c Inverse Fourier transform (iFT) image shown in the same area of (b), and it is calculated from the characteristic spots corresponding to 4a0 × 4a0 periodic patterns in the FT image (Supplementary Fig. 2b). d A set of tunneling spectra measured along the purple line in (a) (Vset = −1 V, and Iset = 100 pA). The spectra are offset for clarity. e Difference spectra of the tunneling spectra in (d) by subtracting the first spectrum as the background. They are presented in a narrow bias range in order to show the detailed structure at low energies near EF. All the data are taken by using a SP Cr tip.
In the sample with a slightly higher doping level of p = 0.10, the AF order almost disappears and more 4a0 × 4a0 plaquettes appear in the mapping of LDOS with a bias of 25 mV (Fig. 3a). Checkerboard modulations appear in more than half area of the presented region, and the rest area is featureless with weak intensity of LDOS at this energy. Upon closer inspection, each 4a0 × 4a0 plaquette exhibits a unique pattern, i.e., there are two or three unidirectional bars of enhanced DOS within the plaquette forming a nematic electronic state. The distance between two neighbored bars is clearly larger than a0 and is about 4a0/3, which leads to an incommensurate modulation. Here in each plaquette, three bars are all along one of the crystalline axes (a- or b- axis, namely the Cu-O-Cu direction), hence, the existence of such unidirectional bars breaks the fourfold symmetry of the crystal. We regard this pattern containing unidirectional bars as local nematicity. However, these nematic patterns are orthogonal to each other among different plaquettes. Figure 3b shows the FT pattern of the dI/dV mapping in Fig. 3a. The spots of Q’ = (±1/4, 0)2 π/a0 or (0, ±1/4)2 π/a0 correspond to the 4a0 × 4a0 checkerboard modulations; those of Q” = (±3/4, 0)2 π/a0 or (0, ±3/4)2 π/a0 correspond to the internal 4a0/3 nematic modulations. In Fig. 3c, we show a set of spectra along the arrowed line across one 4a0 × 4a0 plaquette as marked in Fig. 3a. In the featureless region, the spectra show Mottness gapped feature which is similar to the AF region of UD08. In the region with the enlightened DOS, namely the plaquette, wide spreading DOS with a maximum at about 200 mV appear. This forms a pseudogap feature. In Fig. 3d, we show the same line-scan spectra by subtracting the one in the featureless region (Mottness gapped region). One can see that a hump-like feature of DOS appears near the Fermi level, which indicates the enhancement of DOS near the Fermi level in the 4a0 × 4a0 plaquette. This type of local nematic structure was also observed in overdoped Bi220136; the authors there regarded this kind of pattern as a stripy structure and linked them with the pair density wave. In addition, the observed nematic structure here is local and confined within one plaquette, which seems different from the “stripe phase” seen by neutron scattering in La1.6-xNd0.4SrxCuO437. In the “stripe phase”, there are hole derivative charge chains neighbored by AF patterns or stripes with anti-phase spin directions on the boundary. This has not been observed in our spin-deference topographies. However, our observation about the internal nematic states is in general consistent with the charged magnetic domain or stripy patterns of electronic states in lightly underdoped Mott insulator38,39. Based on the descriptions above, we can outline a general evolution of the electronic states versus hole doping. There are generally three types of electronic states on the surface: (i) the long range AF ordered regions with a charge transfer gapped feature; (ii) the regions without AF order but with finite DOS in a wide energy region (a hump appears in the energy scale of ~200 meV); (iii) the regions with the 4a0 × 4a0 plaquettes and internal nematic electronic structures appearing especially at low energies.
a Differential conductance mapping measured at 25 mV (Vset = −250 mV, and Iset = 100 pA). b The FT pattern of the dI/dV mapping shown in (a). Q’ spots correspond to the checkerboard patterns with the period of 4a0 in the real space, while Q” spots correspond to the nematic modulation with the period of 4a0/3 in the real space. c Spatially resolved tunneling spectra measured along the arrowed line in (a) at Vset = −1 V, and Iset = 100 pA. The spectra are offset for clarity. d Difference spectra of the tunneling spectra in (c) by subtracting the first spectrum as the background. They are presented in a narrow bias range near EF. All the data are taken by using a Cr tip.
Low-energy gap emerging from confined nematic states within a plaquette
In the following, let’s have a close scrutinizing on the internal electronic structure of a 4a0 × 4a0 plaquette measured by a tungsten tip. Figure 4a shows the dI/dV mapping measured at 25 mV in an area of UD10, one can see many such plaquettes, within some plaquettes we can clearly see the unidirectional bars of DOS. The black dots here denote the positions of Bi atoms measured from the topography (Supplementary Fig. 3), and as aforementioned, they are supposed to correspond to the positions of Cu atoms in the Cu-O layer underneath the Bi-O layer20,21,22,23. The oxygen sites on the Cu-O layer are taken in the middle of two neighboring Cu sites. One can see that there are three enlightened bars of DOS with the distance of an incommensurate period of about 4a0/3, and the central bar locates on and aligns along the central Cu-O-Cu chain. We select one of these plaquettes shown in Fig. 4a to do more detailed measurements of spectra, as shown in Fig. 4b, the three bars of higher DOS within the plaquette can be clearly seen. Afterwards, more spectra are measured along different Cu-O-Cu chains numbered as b1 to b5 and shown in Fig. 4c–g. The spectra measured in the 4a0 × 4a0 plaquette generally show a finite DOS with a V-shaped feature in the displayed energy window spanning to 240 meV. When the spectra are measured along b1 and b5, namely on the Cu-O-Cu chains at the edge of the plaquette, one can see that it reveals a large V shape of LDOS with a maximum in the region of about 200 mV (Fig. 4c,g). When we move to b2 and b4, a pair of low-energy coherence-like peaks of dI/dV arise in the central region with the peak energy at about 25 meV (Fig. 4d,f). The most pronounced peaks appear on b3 (Fig. 4e), and that is on the central bar (also the central Cu-O-Cu chain). This is one of the key findings here. A comparison of the spectra measured on one of the central oxygen (O2) and the copper at the edge (Cu5) along b3 is shown in Fig. 4h, and a drastic difference can be clearly seen. To emphasize these low-energy peaks, we take a subtraction with the spectrum at Cu5 from that at O2, and show it as the inset in Fig. 4h. A sharp peak at about 25 mV can again be clearly seen. On the negative bias side, this peak is also present, but it looks less pronounced compared with the positive side, which is induced by a much steeper background on the side of negative bias due to the charge transfer band. The systematic evolution of spectra within the selected plaquette shown in Fig. 4b gives just a representative one, and control experiments have been repeated in more than 10 plaquettes. It clearly demonstrates that there is an internal nematic structure with enlightened bars of LDOS along the Cu-O-Cu chains, and the central one has the highest DOS peaks at about 25 mV.
a An enlarged view of the dI/dV mapping measured at 25 mV (Vset = −250 mV, and Iset = 100 pA). Black dots represent the positions of Bi atoms obtained in the topography taken simultaneously with the dI/dV mapping, and the lattice is distorted due to the supermodulation on the top surface. Cu atoms underneath are supposed to be at the same positions as Bi atoms on the surface. The red square indicates a typical plaquette of 4a0 × 4a0. b A detailed structure of the 4a0 × 4a0 plaquette highlighted in (a). Three- nematic-modulation structure can be seen as bright bars. The positions of some oxygen atoms (marked by crosses) are determined as the middle points of the neighboured Cu atoms roughly along the b-axis. c–g Tunneling spectra measured at the positons of Cu/O atoms along five Cu-O-Cu chains (b1-b5) roughly in the direction of the b-axis within the typical plaquette. h Tunneling spectra measured at O2 and Cu5 positions in b3 chain. The O2 position in b3 chain is in the brightest bar, and the Cu5 position is away from three bright bars. The inset shows the difference spectrum of these two tunneling spectra. All the data are taken by using a tungsten tip.
We have witnessed that a low-energy gap appears with the DOS peak at about 25 mV. Next, we want to illustrate that the differential conductance corresponding to the peak is the highest at the oxygen O2 and O3 (Fig. 4e). In order to figure out the spatial dependence of LDOS more rigorously, we digitize the spatially dependent differential conductance at 25 mV along b3 in the central bar of the selected plaquette and show it in Fig. 5a. Surprisingly, some peaks and knees of differential conductance measured at 25 mV appear at or near the oxygen sites (O1, O2 and O3). This is another key finding in our present study, strongly suggesting that the emerging low-energy DOS through hole doping locate mainly on the oxygen sites, especially on O2 and O3. Since the doped holes are expected to reside in the px or py orbitals which should have nodes in the middle, and ideally there should exist two maxima of DOS on the two lobes. But the resolution of our technique is limited to resolve this internal structure, and we detect a global maximum of DOS at the oxygen sites. We then use the multi-peak Gaussian fitting method to obtain the possible peak positions of the experimental data (red circles in Fig. 5a), and the fitting result is shown as the blue solid line. One can see that the fitting curve coincides with the experimental results very well, and the resultant three Gaussian functions have the central positions very near the three oxygen atoms. We have also conducted line cuts along the central bars of different plaquettes, most of them show the peaks or knees of differential conductance on the oxygen sites, especially on O2 and O3 (eight of them are shown in supplementary Fig. 4 as control experiments). It should be noted that the experimental data obtained by using a SP Cr tip reach the similar conclusion (Supplementary Fig. 5). One may argue that, the Cu atoms may not sit exactly below the Bi atoms, thus the measured differential conductance at the Bi and O atoms in the top layer may not reflect the signal from the Cu and O atoms underneath. To remove this concern, we take the data of spatial dependence of differential conductance along a straight line in the middle of the central bar which is supposed to coincide with a perfect Cu-O-Cu chain (Supplementary Fig. 6). One can see that the peaks or knees of dI/dV still locate near oxygen sites, just like that shown in Fig. 5a. Our data directly prove that the doped holes are really going into the oxygen orbitals, as proposed theoretically by Emery40 and Zhang-Rice41. Thus we can conclude that the doped holes induce some low-energy DOS mainly accommodating at oxygen sites, and these DOS show a low-energy pseudogap feature at about ±25 meV.
a Determination of the local DOS distribution on atomic sites by the multi-peak Gaussian fitting. The differential conductance at 25 mV along the b3 Cu-O-Cu chain (red filled circles taken from Fig. 4b) can be well fitted by the blue solid line constructed by three assembled Gaussian functions (red, pink and green solid lines) with peak positions locating at oxygen sites (blue solid lines). b Cartoon picture showing three bars of enhanced DOS with nematic modulations as highlighted by yellow ellipsoids in atomic scale. The enhanced DOS at about ±25 meV around the central O2 and O3 atoms are highlighted by the yellow-green patches. c Schematic picture of the DOS induced by the chemical doping emerging near EF within the charge transfer gap. The inset shows the spectrum measured on the O2 atom revealing a coherence-like peak of DOS at about ±25 mV.
Discussion
In our experiments, we have made three key observations. Firstly, we find that the AF order is closely related to the Mottness derived charge transfer gap; when the AF order is diminished by hole doping, this gap progressively fills in, i.e. the DOS increases over a wide range of energies. Secondly, at a higher doping level, for example in UD10, the AF order is destroyed, the charge transfer gap is completely filled in and a maximum in the DOS appears at around 200 mV; we call this a large pseudogap. Doping also induces translations symmetry breaking motifs in the DOS consisting of 4a0 × 4a0 plaquettes; within each plaquette, an internal nematic electronic state is observed associated with sharp peaks of DOS at energies of about 25 meV. It is interesting to note that, a large pseudogap feature was also observed in the iridate system (Sr1−xLax)2IrO4 when the Mott gap is filled by doping with electrons42, suggestive of a universal behavior in doping a Mott insulator. Thirdly, the highest DOS peaks appear on the oxygen sites, implying that the holes are likely doped into the oxygen orbitals. The internal nematic structure with three incommensurate unidirectional bars of low-energy DOS within the 4a0 × 4a0 plaquette gives rise to FT spots at Q” = (±3/4, 0)2 π/a0 or (0, ±3/4)2 π/a0. To strengthen this argument, we did careful measurements on the distance between these bright bars (four from Fig. 4b and five from Supplementary Fig. 5b), the averaged distance is about 1.29a0, which is close to the expected (4/3)a0. Similar scattering spots have actually been observed in previous experiments in different systems21,25,34,36, and they are sometime interpreted as a d-form factor density wave43,44. However, our results show an explicit spatial distribution of this structure.
Concerning the low-energy DOS with a gapped feature around ±25 meV, it is probably induced by some kinds of density wave27,28, either through the Fermi surface nesting30,31, or a pair density wave. Therefore, our results illustrate explicitly the evolution and an atomically resolved pattern of the correlated electronic state when holes are doped into the Mott insulator. Since the differential conductance peaks at low energies look like the coherence peaks in the superconducting samples26,45, one of the possibilities to explain our data is to link them with the local pairing. In this context, the low-energy gap can be either the one arising from the PDW or the precursor gap for superconductivity. In this case, considering the fact that we have not seen a superconducting transition yet, it would presumably reflects a very small superfluid stiffness in the present samples, and the resulting suppression of long-range order (“condensation”). The local and confined nematic electronic states observed here may share the same origin as the PDW observed in superconducting state13,14,36. Based on these observations, a schematic plot of the local DOS is shown in Fig. 5b with the yellow-green elongated ellipses highlighting the locations at which higher deferential conductance is observed. This nematic state within a 4a0 × 4a0 plaquette is conjectured to reflect the local electronic pattern associated with pairing induced by doped holes. We base this conjecture on the following observations: (1) Superconductivity is just about to appear when the doping level is about p = 0.10. By counting the hole densities, the state with p = 0.125 would have about 2 holes/plaquette if the space were fully occupied by these plaquettes. To strengthen this argument, we did an estimate of the number of 4a0 × 4a0 plaquettes in the sample UD10; this counting gives a value of about p = 0.095 if we assume 2 holes occupying one plaquette (Supplementary Fig. 7). (2) There are sharp DOS peaks appearing at about ±25 mV (Fig. 5c); these gaps are a bit higher than the superconducting gap measured in Bi2201 superconducting samples45. However, we emphasize that we cannot directly identify the gap at about 25 mV with the superconducting one since the sample is still not superconducting. Thus this low-energy gap most likely arises from a PDW or a low-energy pseudogap for the forthcoming superconductivity in samples with slightly higher doping levels. In superconducting samples with higher doping concentrations, the differential conductance peaks become shaper with a smaller gap value26,45. It remains to be explored how the tunneling spectrum measured in our sample UD10 at the threshold for superconductivity evolves into the one with sharper coherence peaks in the superconducting samples at higher doping levels.
Regarding the evolution of electronic state in the lightly doped Mott insulator and how the pairing is established, actually we do not have a clear answer yet. Hopefully our experiment contributes new understanding towards this goal. In these very underdoped samples, there exists quite clear evidence for electronic inhomogeneity, which is particularly clear in the sample UD08 with data measured with a spin-polarized STM, see, for example, Fig. 2a,b and Fig. 3a. By doping holes, our measurements reveal that the AF order is destroyed, but in a way that is suggestive of electronic phase separation. This kind of electronic inhomogeneity has been anticipated in strongly correlated systems. It has long been perceived that the superconductivity in cuprates arises from diluted superfluid density on top of a strong pairing background46,47,48, and this is consistent with strong superconducting fluctuations in the underdoped region49,50. Furthermore, it was theoretically proposed that electronic phase separation can be induced by frustrated quantum interactions in extremely underdoped cuprates7, and then the doped holes may appear in the conducting stripes or domain walls7,37,38. These doped holes may locally pair in the conducting stripes, forming the upcoming superconductivity8,37,38. Despite the existence of inhomogeneity in extremely underdoped samples, we strongly believe that the observed 4a0 × 4a0 plaquettes, and the internal structure at low energies, are intrinsic features because they appear to be more and more regular and populated with higher doping. Thus an assembled picture would be that the local pairing is established through doped holes on a background with strong magnetic superexchange coupling, leading to the formation of the 4a0 × 4a0 plaquette with an internal nematic structure measured at low energies. Actually, a recent theoretical approach finds that unconventional superconductivity is spectacularly enhanced if the hopping matrix elements (corresponding to the coherent weight here) are periodically modulated in a stripe-like pattern, which shows further consistency with our results51. Concerning the local pairing and pseudogap in underdoped region, some Hubbard-model based theoretical treatments involving either local orbital structure52 or degenerate plaquette physics53 were proposed, these may help to understand the confined nematic electronic states observed in present work. Our experimental observations, including the local electronic state composed by many plaquettes with a confined nematic state, should trigger future theoretical efforts to understand the physics of doped Mott insulators, and help to unravel the puzzle of Cooper pairing in the cuprate superconductors.
Methods
Sample and tip preparation
The single crystals of Bi2Sr2−xLaxCuO6+δ were grown by using the traveling-solvent floating-zone technique17. The samples look very shiny with a very good crystallinity checked by x-ray diffraction pattern. STM/STS measurements were carried out in a scanning tunneling microscope (USM-1300, Unisoku Co., Ltd.) with the ultrahigh vacuum up to 10−10 torr. During the STM experiment, we used two kinds of electrochemically etched tips, i.e., the spin-polarized chromium tip54 and the conventional tungsten tip. The Cr tip was electrochemically etched by 3 mol/L NaOH solution with the immersed end covered by a polytetrafluoroethylene tube with a certain length55. After the etching, the Cr tip was transferred into the STM chamber, and before each spin-difference measurement, the spin polarization feature was characterized on the cleaved surface of single crystalline Fe1+xTe15,16,56 in order to see the well-known AF order. The magnetic field is applied perpendicular to the surface (ab plane) of the sample during the measurements. The STM data are taken at about 2.0 K by using the chromium tip, and those are taken at about 1.6 K by using the tungsten tip. A typical lock-in technique is used with an ac modulation of 987.5 Hz.
Data availability
Data measured or analyzed during this study are available from the corresponding authors on reasonable request. Source data are provided with this paper.
References
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Anderson, P. W. et al. The physics behind high-temperature superconducting cuprates: the ‘plain vanilla’ version of RVB. J. Phys.: Condens. Matter 16, R755–R769 (2004).
Wen, X.-G. & Lee, P. A. Theory of underdoped cuprates. Phys. Rev. Lett. 76, 503 (1996).
Scalapino, D. J. Superconductivity and spin fluctuations. J. Low. Temp. Phys. 117, 179–188 (1999).
Abanov, A., Chubukov, A. V. & Norman, M. R. Gap anisotropy and universal pairing scale in a spin-fluctuation model of cuprate superconductors. Phys. Rev. B 78, 220507(R) (2008).
Dahm, T. et al. Strength of the spin-fluctuation-mediated pairing interaction in a high-temperature superconductor. Nat. Phys. 5, 217–221 (2009).
Emery, V. J. & Kivelson, S. A. Frustrated electronic phase separation and high-temperature superconductors. Phys. C. 209, 597–621 (1993).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Berg, E., Fradkin, E. & Kivelson, S. A. Theory of the striped superconductor. Phys. Rev. B 79, 064515 (2009).
Agterberg, D. F. & Tsunetsugu, H. Dislocations and vortices in pair density wave superconductors. Nat. Phys. 4, 639–642 (2008).
Chen, H.-D., Vafek, O., Yazdani, A. & Zhang, S.-C. Pair density wave in the pseudogap state of high temperature superconductors. Phys. Rev. Lett. 93, 187002 (2004).
Vershinin, M. et al. Local ordering in the pseudogap state of the high-Tc superconductor Bi2Sr2CaCu2O8+δ. Science 303, 1995–1998 (2004).
Hamidian, M. H. et al. Detection of a cooper-pair density wave in Bi2Sr2CaCu2O8+x. Nature 532, 343–347 (2016).
Du, Z. et al. Imaging the energy gap modulations of the cuprate pair-density-wave state. Nature 580, 65–70 (2020).
Wan, S. et al. Direct visualization of a static incommensurate antiferromagnetic order in Fe-doped Bi2Sr2CaCu2O8+δ. Proc. Natl. Acad. Sci. USA. 118, e2115317118 (2021).
Li, H. et al. No observation of chiral flux current in the topological kagome metal CsV3Sb5. Phys. Rev. B 105, 045102 (2022).
Luo, H., Cheng, P., Fang, L. & Wen, H.-H. Growth and post-annealing studies of Bi2Sr2-xLaxCuO6+δ (0 ≤ x ≤ 1.00) single crystals. Supercond. Sci. Technol. 21, 125024 (2008).
Kawasaki, S., Lin, C. T., Kuhns, P. L., Reyes, A. P. & Zheng, G.-Q. Carrier-concentration dependence of the pseudogap ground state of superconducting Bi2Sr2-xLaxCuO6+δ revealed by 63,65Cu-nuclear magnetic resonance in very high magnetic fields. Phys. Rev. Lett. 105, 137002 (2010).
Peng, Y. et al. Disappearance of nodal gap across the insulator–superconductor transition in a copper-oxide superconductor. Nat. Commun. 4, 2459 (2013).
Gao, Y., Lee, P., Coppens, P., Subramania, M. A. & Sleight, A. W. The incommensurate modulation of the 2212 Bi-Sr-Ca-Cu-O superconductor. Science 241, 954–956 (1988).
Kohsaka, Y. et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science 315, 1380–1385 (2007).
Slezak, J. A. et al. Imaging the impact on cuprate superconductivity of varying the interatomic distances within individual crystal unit cells. Proc. Natl. Acad. Sci. USA. 105, 3203–3208 (2008).
Hamidian, M. H. et al. Picometer registration of zinc impurity states in Bi2Sr2CaCu2O8+δ for phase determination in intra-unit-cell Fourier transform STM. N. J. Phys. 14, 053017 (2012).
Zeljkovic, I. et al. Scanning tunnelling microscopy imaging of symmetry-breaking structural distortion in the bismuth-based cuprate superconductors. Nat. Mater. 11, 585–589 (2012).
Hanaguri, T. et al. A ‘checkerboard’ electronic crystal state in lightly hole-doped Ca2-xNaxCuO2Cl2. Nature 430, 1001–1005 (2004).
Wise, W. D. et al. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 4, 696–699 (2008).
Comin, R. et al. Charge order driven by Fermi-arc instability in Bi2Sr2-xLaxCuO6+δ. Science 343, 390–392 (2014).
da Silva Neto, E. H. et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 343, 393–396 (2014).
Hoffman, J. E. et al. A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+δ. Science 295, 466–469 (2002).
Wise, W. D. et al. Imaging nanoscale Fermi-surface variations in an inhomogeneous superconductor. Nat. Phys. 5, 213–216 (2009).
Webb, T. A. et al. Density wave probes cuprate quantum phase transition. Phys. Rev. X 9, 021021 (2019).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Battisti, I. et al. Poor electronic screening in lightly doped Mott insulators observed with scanning tunneling microscopy. Phys. Rev. B 95, 235141 (2017).
Kohsaka, Y. et al. Visualization of the emergence of the pseudogap state and the evolution to superconductivity in a lightly hole-doped Mott insulator. Nat. Phys. 8, 534–538 (2012).
Cai, P. et al. Visualizing the evolution from the Mott insulator to a charge-ordered insulator in lightly doped cuprates. Nat. Phys. 12, 1047–1051 (2016).
Li, X. et al. Evolution of charge and pair density modulations in overdoped Bi2Sr2CuO6+δ. Phys. Rev. X 11, 011007 (2021).
Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563 (1995).
Zaanen, J. & Gunnarsson, O. Charged magnetic domain lines and the magnetism of high-Tc oxides. Phys. Rev. B 40, 7391 (1989).
Emery, V. J., Kivelson, S. A. & Tranquada, J. M. Stripe phases in high-temperature superconductors. Proc. Natl. Acad. Sci. USA. 96, 8814–8817 (1999).
Emery, V. J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 58, 2794 (1987).
Zhang, F. & Rice, T. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759(R) (1988).
Battisti, I. et al. Universality of pseudogap and emergent order in lightly doped Mott insulators. Nat. Phys. 13, 21–26 (2017).
Fujita, K. et al. Direct phase-sensitive identification of a d-form factor density wave in underdoped cuprates. Proc. Natl. Acad. Sci. USA. 111, E3026–E3032 (2014).
Hamidian, M. H. et al. Atomic-scale electronic structure of the cuprate d-symmetry form factor density wave state. Nat. Phys. 12, 150–156 (2016).
Kugler, M., Fischer, Ø., Renner, C., Ono, S. & Ando, Y. Scanning tunneling spectroscopy of Bi2Sr2CuO6+δ: new evidence for the common origin of the pseudogap and superconductivity. Phys. Rev. Lett. 86, 4911 (2001).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Deutscher, G. Coherence and single-particle excitations in the high-temperature superconductors. Nature 397, 410–412 (1999).
Feng, D. L. et al. Signature of superfluid density in the single-particle excitation spectrum of Bi2Sr2CaCu2O8+δ. Science 289, 277–281 (2000).
Xu, Z. A., Ong, N. P., Wang, Y., Kakeshita, T. & Uchida, S. Vortex-like excitations and the onset of superconducting phase fluctuation in underdoped La2-xSrxCuO4. Nature 406, 486–488 (2000).
Wen, H.-H. et al. Specific-heat measurement of a residual superconducting state in the normal state of underdoped Bi2Sr2-xLaxCuO6+δ cuprate superconductors. Phys. Rev. Lett. 103, 067002 (2009).
Jiang, H.-C. & Kivelson, S. A. Stripe order enhanced superconductivity in the Hubbard model. Proc. Natl. Acad. Sci. USA. 119, e2109406119 (2021).
Mai, P., Balduzzi, G., Johnston, S. & Maier, T. A. Orbital structure of the effective pairing interaction in the high-temperature superconducting cuprates. NPJ Quantum Mater. 6, 26 (2021).
Danilov, M. et al. Degenerate plaquette physics as key ingredient of high-temperature superconductivity in cuprates. NPJ Quantum Mater. 7, 50 (2022).
Schlenhoff, A., Krause, S., Herzog, G. & Wiesendanger, R. Bulk Cr tips with full spatial magnetic sensitivity for spin-polarized scanning tunneling microscopy. Appl. Phys. Lett. 97, 083104 (2010).
Huang, D., Liu, S., Zeljkovic, I., Mitchell, J. F. & Hoffman, J. E. Etching of Cr tips for scanning tunneling microscopy of cleavable oxides. Rev. Sci. Instrum. 88, 023705 (2017).
Enayat, M. et al. Real-space imaging of the atomic-scale magnetic structure of Fe1+yTe. Science 345, 653–656 (2014).
Acknowledgements
We thank H. Luo for the efforts in growing the single crystals, and we also acknowledge helpful discussions with Z.-Y. Weng, T. Xiang, J. Schmalian, I. Eremin. Thanks go specially to Steven Kivelson for the useful message and efforts in improving the paper. This work was supported by National Natural Science Foundation of China (11927809, ER46311401,11974171), the state key project from the Ministry of Science and Technology of China (2022YFA1403200) and Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000).
Author information
Authors and Affiliations
Contributions
STM/STS measurements and analysis were performed by Huazhou Li, Han Li, Z.W., S.W., H.Y. and H.-H.W. Han Li and Z.W. measured transport properties of samples. H.-H.W., H.Y. and Huazhou Li wrote the paper. H.-H.W. coordinated the whole work. All authors have discussed the results and the interpretations.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, H., Li, H., Wang, Z. et al. Low-energy gap emerging from confined nematic states in extremely underdoped cuprate superconductors. npj Quantum Mater. 8, 18 (2023). https://doi.org/10.1038/s41535-023-00552-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-023-00552-z
This article is cited by
-
High Tc superconductivity in Copper oxides: the condensing bosons as stripy plaquettes
npj Quantum Materials (2023)