Abstract
In a thin Weyl semimetal, a thickness dependent Weyl-orbit quantum oscillation was proposed to exist, originating from a nonlocal cyclotron orbit via electron tunnelings between top and bottom Fermi-arc surface states. Here, magneto-transport measurements were carried out on untwinned Weyl metal SrRuO3 thin films. In particular, quantum oscillations with a frequency Fs1 ≈ 30 T were identified, corresponding to a small Fermi pocket with a light effective mass. Its oscillation amplitude appears to be at maximum for thicknesses in a range of 10 to 20 nm, and the phase of oscillation exhibits a systematic change with film thickness. The constructed Landau fan diagram shows an unusual concave downward curvature in the 1/μ0Hn-n curve, where n is the Landau level index. From thickness and field-orientation dependence, the Fs1 oscillation is attributed to be of surface origin. Those findings can be understood within the framework of the Weyl-orbit quantum oscillation effect with non-adiabatic corrections.
Similar content being viewed by others
Introduction
The phenomena of quantum oscillations with magnetic field in matters were first discovered in bismuth more than 90 years ago1, and it was soon realized that such phenomena can be used as a measure for the Fermi surface in momentum space1,2. Quantitatively, quantum oscillatory phenomena are described by the general expression of Δρ ∝ Dcos[\(2\pi (\frac{F}{{\mu }_{0}H}+\delta )\)], where D is the damping factor, F is the oscillation frequency, and δ is the phase shift of the oscillation associated with individual extremal areas of the Fermi surface in momentum space. In theory, the absolute value of δ is a consequence of the underlying band structure and dimensionality of the material under study in which the Berry phase is derived as 0 or π. From a modern point of view, the periodic oscillation of either ρ or magnetization with respect to the inverse of a magnetic field is a quantum effect deriving from the Bohr-Sommerfeld quantization rule on electrons’ cyclotron motions, where the requirement of the single-valued wave function gives rise to discrete energies for electrons3. The oscillation frequency (F) can be linked directly to the extremal cross-sectional area (Ae) of the Fermi surface by Onsager’s relation of F = ℏAe/2πe. In addition, the amplitude and phase of quantum oscillations encode the information about the electronic band topology at the Fermi surface2 that has been a major subject recently in the field of topological materials4,5.
In topological Dirac and Weyl semimetals, a nontrivial conical band with linear dispersion results in a π Berry phase that is picked up during the cyclotron motion and thus causes a phase shift by half a period in the quantum oscillation, which has been reported by several quantum oscillations experiments6,7. One practical approach for the determination of δ is to construct the Landau fan diagram, which plots the 1/μ0H values for peaks and valleys in the quantum oscillations (1/μ0Hn) as a function of the corresponding Landau level (LL) index n. δ can then be determined from the intercept (n0) as 1/μ0Hn approaches zero by extrapolating the curve of 1/μ0Hn versus n. As pointed out by several authors8,9, the peaks (valleys) in the ρ (conductivity) oscillations should be assigned with integer numbers of n for a three-dimensional (3D) system, and thus δ = n0 ≈ ±1/8 and ±5/8 for a conical band with π Berry phase and a trivial parabolic band with zero Berry phase, respectively.
On the other hand, Weyl semimetals (WSMs) are also known for their unusual Fermi-arc surface states10,11 that connect the projected pair of Weyl nodes on a surface. An unusual type of quantum oscillation due to the so-called Weyl-orbit effect (WOE) was first theoretically predicted12 and soon demonstrated by experiments in Dirac semimetal Cd3As213,14,15. The WOE results from an intriguing collaboration between the Fermi-arc surface states and the Weyl-node bulk states, where a nonlocal cyclotron orbit gives rise to a new type of quantum oscillation. One important consequence for WOE is the thickness dependence on the phase of the quantum oscillations, but, unfortunately, such a phase shift can be easily smeared out by a small density variation in different samples16. It is, therefore, important to grow high crystalline thin films of WSM, and the WOE can then be carefully investigated on WSM films with different thicknesses. While there are recent reports about possible topological and correlated phases in ruthenates17,18, the ferromagnetic oxide of SrRuO3 (SRO)19,20 appears to be another promising candidate. The nonmonotonic temperature (T) dependence of both anomalous Hall conductivity21 and spin wave gap in SRO22 suggest the presence of the Weyl nodes near the Fermi surface that coexists with other 3D bulk Fermi pockets, making SRO a candidate for the Weyl metal phase. In addition, quantum oscillations of ρ in SRO thin films on SrTiO3 (STO) (001) substrate also revealed an unusual F ≈ 30 T23,24 that is equivalent to a small Fermi pocket with a bulk density of only 9.3 × 1017 cm−3 for the 3D case. Such a small Fermi pocket seems to be in line with the Weyl metal phase in SRO, but its origin remains an open question. In this work, a series of highly crystalline and untwinned SRO films with different thicknesses (ts) ranging from about 7.7–35.3 nm were grown on miscut STO (001) substrates using adsorption-controlled growth by an oxide molecular beam epitaxy (MBE) system25,26, where pronounced quantum oscillations in ρ were observed. From detailed angle-dependent quantum oscillations with applied fields up to 35 T, we found that the small Fermi pocket of F ≈ 30 T behaved as a two-dimensional (2D) like Fermi pocket, and the corresponding Landau fan diagram showed a clear concave downward curvature for the curve of 1/μ0Hn versus n. Those results are discussed and compared to the simulated thickness-dependent quantum oscillations based on WOE.
Results
Structure characterizations
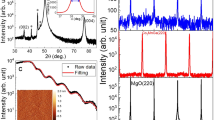
The crystal structure of perovskite SRO is illustrated in the left panel of Fig. 1a, where the rotation and tilting of RuO6 octahedra give rise to an orthorhombic phase at room temperature. When growing on an STO (001) substrate, a compressive strain of about −0.4% in SRO films occurs and gives rise to a distorted orthorhombic phase with Pbnm space group and the crystalline axis of SRO [110]o nearly aligned along the STO [001]c, where the subscripts o and c refer to the orthorhombic- and cubic-phase, respectively19. The right panel of Fig. 1a shows a cross-sectional scanning transmission electron microscope (STEM) high-angle annular dark-field (HAADF) image of an SRO film we grew, indicating an atomically sharp interface between SRO and STO. High-resolution X-ray measurements were performed, and the left panel of Fig. 1b displays the STO (003)c crystal truncation rods (CTRs) for an SRO film with t ≈ 13.7 nm. The abscissa L is in unit of STO reciprocal lattice unit (r.l.u.), representing the momentum transfer along the surface normal. The SRO (330)o reflection appeared at a slightly low-L side of STO (003)c reflection25. The presence of pronounced thickness fringes around the SRO Bragg reflection indicates excellent film crystallinity and sharp interfaces. The oscillation period of about 0.031 r.l.u. gives a crystalline thickness of about 12.6 nm, which is close to t ≈ 13.7 nm as obtained from the X-ray low-angle reflectivity measurements. The right panel of Fig. 1b shows the CTR of SRO (221)o off-normal reflection. The observation of the orthorhombic specific SRO (221)o reflection with pronounced intensity oscillations confirmed the orthorhombic phase and also excellent thickness uniformity and crystallinity of the SRO film27. The corresponding azimuthal ϕ scan across the SRO (021)o reflection is shown in Fig. 1c, where two sets of equally spaced peaks with different peak intensities were observed. This indicates the presence of four orthorhombic twin domains28 as illustrated in Fig. 1d. Be aware that the [110]o direction of orthorhombic SRO can be considered as parallel to the normal of (110)o plane because of the tiny (<0.8%) difference between the length of its a- and b-axis that was highly exaggerated in Fig. 1d. From the peak intensity, the volume fractions for domains A–D are estimated to be about 94.1%, 1.7%, 2.0%, and 2.2%, respectively, which thus justifies the nearly single-domain and untwinned structure in our SRO films. Detailed investigations of the orthorhombic twin domains for SRO films grown on miscut STO (001) substrates have been reported in a separate paper26. On the other hand, the surface morphology of the SRO film with t ≈ 13.7 nm was measured by an atomic force microscope (AFM) as shown in Fig. 1e, where the lower panel shows the cross-section height profile across the red line located in the upper panel of Fig. 1e. The step heights at the terrace edges are about 1–2 unit cells of STO, which again supports for the high thickness uniformity of the SRO film. However, we do note the presence of well-isolated pits that are known to exist for the step-flow growth of SRO film19. By excluding those pits, the averaged roughness of the SRO film can be obtained from the AFM images, and the resulting t-dependence of the averaged roughness is shown in Fig. 2f. For t ≤ 35.3 nm, the average roughness of the film was determined to be less than about 0.3 nm (see Supplementary Note 1). We also note that the dominating domain is found to have SRO [001]o (the black arrow in Fig. 1e) along the terrace edge on an STO substrate. For the growth of SRO films in this work, all the STO substrates were chosen to have a small miscut angle of about 0.1o with the terrace edge being parallel to a lateral STO < 100 > direction to ensure the single-domain in our SRO films26. In addition, the bias current (\(\overrightarrow{{{{\bf{I}}}}}\)) for the transport measurements was set to be perpendicular to the terrace edge as demonstrated in Fig. 2a, i.e. \(\overrightarrow{{{{\bf{I}}}}}\perp\) SRO [001]o, in order to avoid complication and inconsistency due to possible ρ anisotropy and domain dependence in SRO.
a An atomic packing illustration (left) and the cross-sectional STEM HAADF image (right) of (110)o oriented orthorhombic SRO on an STO (001) substrate. The left panel and right panel of b show the CTRs of SRO specular (330)o and off-normal (221)o reflections, respectively. Pronounced fringes persisting over many periods along both CTRs manifest the excellent crystallinity and sharp interfaces of the SRO film. c The azimuthal ϕ scan across SRO (021)o reflection reveals the presence of four orthorhombic twin domains rotated 90o from each other as demonstrated in d (not to scale). The dominant domain A, amounting to 94.1% of volume fraction, has its [001]o direction parallel to the atomic step edges on the STO surface as verified by XRD results as well as the AFM image in e, where the lower panel of e shows the flattened cross-sectional height profile along the red line. The c-axis of SRO lies on the surface and is aligned with one of the STO lateral crystalline axes, [010]c in the present figure. f The thickness dependence of the averaged surface roughness for SRO films from AFM images analyses with uncertainties from the full width at half maximum in height histograms of AFM images. The averaged roughness is <0.3 nm, which does not vary significantly for t ≤ 35.3 nm.
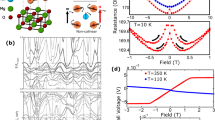
a An illustration of the measurement geometry for ρ and ρxy with respect to the SRO crystalline axes. b The T dependent ρ in SRO(t)/STO (001) with thicknesses ts ranging from about 7.7–35.3 nm. The kink at T ≈ 150 K corresponds to the onset of the ferromagnetism. The upper panel and lower panel of c show the MR and ρxy, respectively, as a function of field at T = 2.5 K, and they share the same color codes as that in (b). Pronounced quantum oscillations were observed for μ0H ≥ 3.5 T in all five SRO films with different t values. d The θ dependent MR for t ≈ 13.7 and 18.7 nm are shown in the upper panel and lower panel, respectively. The inset cartoon shows the definition of the θ angle. For the field perpendicular to the film surface plane (θ = 0o), a large and positive MR was observed, which is practically linear with the field strength up to 35 T without saturation. The magnitude of the positive MR drops with increasing θ, and it becomes a negative MR when the field is applied along the current direction (θ = 90o).
Magnetotransport measurements
The T-dependent ρ exhibits a metallic behavior as shown in Fig. 2b for SRO films with different ts ranging from about 7.7–35.3 nm. The kink at T ≈ 150 K indicates the occurrence of a ferromagnetic transition, which does not vary significantly with t within the range of our interests. At lower temperatures, ρ follows a T2 dependence as predicted for a Fermi liquid system23, and ρ at T = 5 K (ρ(5 K)) shows a progressive increase from ρ(5 K) ≈ 3.8–12.7 μΩ cm as the SRO film thickness decreases from t ≈ 35.3–7.7 nm. ρ in ruthenates is known to show high sensitivity to disorder29, and thus the low ρ(5 K) values indicate the high crystallinity of our SRO films. A positive transverse magnetoresistance (MR) with an applied field \(\overrightarrow{{{{\bf{B}}}}}\parallel\) SRO [110]o was observed for thicker SRO films with t ≥ 10 nm as shown in the upper panel of Fig. 2c for T = 2.5 K, and the MR, defined as [ρ(H)/ρ(H = 0)]−1, can be as large as +74 % at μ0H = 14 T for SRO film with t ≈ 17.6 nm. It gradually decreases with decreasing t, giving an MR of about +24% at μ0H = 14 T for SRO film with t ≈ 11.7 nm. For t ≈ 7.7 nm, the MR first decreases with increasing field to a value of −3% at μ0H ≈ 3.6 T above which increases with field instead, giving a small positive MR ≈ +4% at μ0H = 14 T. On the other hand, the field-dependent Hall resistivity (ρxy) shows a sign change in the Hall slope (dρxy/dμ0H) from negative to positive as μ0H goes from 0 to 14 T, which was plotted in the lower panel of Fig. 2c for T = 2.5 K. Pronounced quantum oscillations were clearly observed in both ρ and ρxy for μ0H ≥ 3 T, which is only possible for highly crystalline SRO films with low residual resistivity23,24. When tilting \(\overrightarrow{{{{\bf{B}}}}}\) toward \(\overrightarrow{{{{\bf{I}}}}}\) by an angle θ as illustrated in the inset cartoon of Fig. 2d, the MR changes from being positive to negative as θ goes from 0o to 90o, as shown in the upper panel and lower panel of Fig. 2d for SRO films with t ≈ 13.7 and 18.7 nm, respectively, at T ≈ 0.3 K. Remarkably, the transverse MR (θ = 0o) is practically H-linear without any tendency of saturation, giving a positive MR of about +158% and +117% for t ≈ 13.7 and 18.7 nm, respectively, at μ0H = 35 T. On the other hand, for θ = 90o with \(\overrightarrow{{{{\bf{B}}}}}\parallel\)\(\overrightarrow{{{{\bf{I}}}}}\), apparent negative MRs were observed in the low field regime, giving a negative MR of about −20% and −5% at μ0H ~ 15 T for t ≈ 13.7 and 18.7 nm, respectively. The H-linear transverse MR and the negative longitudinal MR are reminiscent of the MR behaviors commonly observed in topological Dirac and Weyl semimetals5,24,30,31.
The resulting field-dependent conductivity (\(\sigma \equiv \rho /({\rho }^{2}+{\rho }_{{{{xy}}}}^{2})\)) for the three different ts ranging from 9.0 to 18.7 nm at T = 0.3 K is shown in the upper panel of Fig. 3a. In zero field, σ equals about 9.3 × 106 Ω−1 m−1 for t ≈ 9.0 nm, and it increases with t, giving a σ ≈ 22.6 × 106 Ω−1 m−1 for t ≈ 18.7 nm. σ drops with increasing fields up to 35 T, and the corresponding dσ/dH versus μ0H was plotted in the lower panel of Fig. 3a, where pronounced quantum oscillations were observed for μ0H ≥ 3.5 T. By taking the fast Fourier transform (FFT) on the curves of dσ/dH versus 1/μ0H, several distinct frequencies of Fs1 and F1−5 can be clearly identified from the FFT spectra as shown in Fig. 3b. The oscillations with F1−5 frequencies ranging from ≈ 300 to 7400 T appeared to show up when μ0H ≥ 12 T with the oscillation amplitudes grow with increasing film thickness t. On the other hand, the oscillation for Fs1 ≈ 30 T starts at a much lower field of ≈3.5 T, and it appears to vanish when the field is above a critical value of Bc ~ 15 T. Following the standard practice, the effective mass (m*) and Dingle temperature (TD) can be determined from the damping of the quantum oscillations1. From the temperature-dependent measurements, the effective mass was determined to be m* = (0.30 ± 0.01)me for Fs1, where me is the electron mass. On the other hand, the extracted m* values for the Fermi pockets with F ≈ 300 and 3680 T are more than tenfold larger with m* = (3.2 ± 0.3) and (5.5 ± 0.8)me, respectively (see Supplementary Note 2). A summary of the extracted parameters from quantum oscillation data is shown in Table 1. τq ≡ ℏ/2πkBTD is the quantum lifetime. The resulting ℓq ≡ (ℏkF/m*)τq is the quantum mean free path, and the Drude mean free path ℓd was calculated using a bulk density of about 6.1 × 1021 cm−3 for all ts. At T = 2.5 K, ℓq falls in a range from 31 to 62 nm with a relatively weak dependence on t as demonstrated in the middle panel of Fig. 3c. On the contrary, ℓd at T = 2.5 K monotonically increases by nearly four-fold from 31 to 118 nm as t increases from 7.7 to 35.3 nm.
The upper panel of a shows the field dependent σ with fields up to 35 T for three SRO films with different t values, and the corresponding dσ/d(μ0H) versus μ0H were plotted in the lower panel, where pronounced quantum oscillations were observed for μ0H ≥ 3.5 T. The upper panel and lower panel of b show the FFT spectra in the low-frequency region and high-frequency region, respectively. The quantum oscillation for Fs1 (about 30 T) dominates in the low field region, and it seems to vanish for μ0H ≥ 15 T. Other frequencies of F1–F5 appears when μ0H ≥ 12 T. c A summary of the thickness dependence of extracted mean free path and FFT amplitudes are shown in the middle-panel and lower-panel, respectively. The uncertainty in the quantum means free path came from the standard deviation in the fitting to the damping term. The nonmonotonic variation of the FFT amplitude for Fs1 with t is in big contrast to the nearly t-linear dependence for F3 and F4. The corresponding RRR and ρ(2.5 K) as a function of t were plotted in the upper panel of (c).
Figure 3c summarizes the thickness dependence of residual resistivity ratio (RRR ≡ ρ(300 K)/ρ(5 K)) (upper panel), mean free path (middle panel), and FFT amplitudes (lower panel). As t increases from 7.7 to 35.3 nm, the RRR follows an increasing trend from 14.4 to 51.6, and the corresponding ρ(2.5 K) decreases from 12.3 to 3.2 μΩ cm. The observed values of Fs1, Fs2, F3, and F4 show relatively weak t-dependence, but the FFT amplitude for Fs1 appears to show nonmonotonic t dependence. In particular, for 10 ≤ t ≤ 20 nm, the FFT amplitude for Fs1 is maximal with a weak t dependence, regardless of a nearly 50% variation in RRR as shown in the upper panel of Fig. 3c. This is in sharp contrast to the nearly t linear dependence of FFT amplitudes for F3 and F4 as expected for 3D bulk pockets with increased RRR and t up to about 20 nm, and, in principle, it shall increase monotonically with larger t for t ≥ 20 nm that calls for more high field measurements up to 35 T. Nevertheless, from the current data shown in the lower panel of Fig. 3c, such a nonmonotonic t dependence on the FFT amplitude indicates that the quantum oscillation for Fs1 is unusual and more likely to be the surface origin.
Electronic band calculations
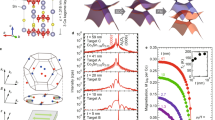
We have calculated electronic structures using first-principles methods32,33,34,35,36. For U = 3.4 eV and J = 0.68 eV, we obtain a ferromagnetic (FM) ground state with the magnetic moment on Ru sites close to 1.20μB, which agrees well with our experiments and previous DFT study37. Moreover, we find that the ground state energy of the system with the magnetic moment oriented along [110]o direction is slightly lower than that along [001]o direction (\({E}_{110}^{{{{\rm{FM}}}}}-{E}_{001}^{{{{\rm{FM}}}}}\approx -0.546\) meV per f.u.), which is consistent with the observed magnetic easy axis along [110]o in our SRO films. The calculated band structures are shown in Fig. 4a, and a number of Weyl nodes were clearly identified when searching in four subband pairs near the Fermi energy (see Supplementary Note 3). In order to identify the Fermi pockets for the observed quantum oscillations shown in Fig. 3, the kx and ky in the original momentum space were transformed into k∥ and k⊥ with k∥ lying in the (110)o plane. The calculated Fermi surface (FS) sliced along k∥−kz plane with k⊥ = 0 is shown in Fig. 4b with the center being the Γ point. We identified three major pockets of A–C with areas of 48, 72, and 53 nm−2, respectively. The corresponding frequencies are 5077, 7531, and 5517 T, which are relatively close to the observed F3 ≈ 3680 T, F5 ≈ 7400 T, and F4 ≈ 4000 T, respectively, as shown in the lower panel of Fig. 3b. The A and B pockets are well consistent with the observed FS from an earlier angle-resolved photo-emission experiment38. We notice several smaller pockets between the A and B, but, unlike the three major pockets, they changed dramatically as k⊥ varies across the Γ point (see Supplementary Note 4). Therefore, those smaller pockets may not contribute coherently to give observable quantum oscillations. We further moved on to look for possible nonoverlapping Weyl nodes when projecting on (110)o plane. The energy dependence of the Weyl nodes at (k∥, kz) within a window of ∣E−EF∣ ≤ 50 meV is shown in Fig. 4c, where the squares and triangles are Weyl nodes from subband pair II and subband pair III, respectively, with the red (blue) color being the chirality of +1 (−1). A number of nonoverlapping Weyl nodes projected on k∥−kz plane are clearly observed. By selecting the projected Weyl nodes at similar energies with opposite chiralities, four Weyl-node pairs are identified and shown in Fig. 4d, where the black arrows represent wave vectors connecting Weyl-node pairs from +1 to −1. The corresponding Fermi-arc lengths fall in a range from k0 ≈ 0.8–6.5 nm−1. Those band calculation results support the presence of Fermi-arc surface states on (110)o plane, which is essential for the occurrence of WOE. However, we remark that, due to the complex band crossings near the Fermi energy, the Weyl node locations are highly sensitive to several parameters used for the band calculations. Nevertheless, nonoverlapping Weyl-node pairs projected on (110)o plane are always present for different U values ranging from 2 to 3.4 eV (see Supplementary Note 3).
a Band structure near the Fermi energy calculated with spin–orbit coupling in the ferromagnetic ground state with the magnetic moment oriented along [110]o direction. We searched for Weyl nodes in four pairs of bands near the Fermi energy (pair I → green band and the one below; pair II → (green, red); pair III → (red, blue); pair IV → (blue, pink)). b The corresponding FS plot sliced along the k∥-kz plane, which indicates three major pockets of A–C. c Locations of Weyl nodes residing in these four pairs in the energy window of ∣E−EF∣ < 50 meV. The red and blue symbols are Weyl nodes with a chirality of +1 and −1, respectively. d The nonoverlapping Weyl-node pairs projected on k∥−kz plane. The arrows connect from +1 to −1 Weyl nodes at similar energy, where the calculated k0 values and the corresponding Weyl node energies in units of meV are indicated.
Quantum oscillations analyses
For better revelations of the quantum oscillations in σ without subtracting any artificial background, we plot \(-{{{{\rm{d}}}}}^{2}\sigma /{{{\rm{d}}}}{(1/{\mu }_{0}H)}^{2}\) as a function of 1/μ0H as shown in Fig. 5a for SRO films with different ts ranging from about 7.7 to 35.3 nm. The peak and valley locations in the oscillation turn out to show systematic phase shifts to lower 1/μ0H values as t increases, indicated by long dashed lines in Fig. 5a, and an integer number of LL index (n) was assigned to the minimum of −d2σ/d(1/H)25,8. The corresponding FFT spectra for SRO films with different t values are shown in Fig. 5b. A dominant frequency of Fs1 ≈ 30 T was clearly observed, and another frequency of Fs2 ≈ 50 T was also observable with a much smaller FFT amplitude and also broader distribution in the FFT spectra. Therefore, the quantum oscillations for μ0H ≤ 14 T as shown in Fig. 5a are dominated by an unusually small Fermi pocket associated with Fs1, which turns out to show the largest magnitude for t ≈ 17.6 nm. A decrease of the FFT amplitude occurs for t > 20 nm and t < 10 nm as is evident from the results in Fig. 5a. In order to further probe the Fermi pocket associated with Fs1, detailed angle dependence of the quantum oscillations was performed with γ-rotation and θ-rotation setups as illustrated in the inset of Fig. 5e, where \(\overrightarrow{{{{\bf{B}}}}}\) was tilted toward \(\overrightarrow{{{{\bf{I}}}}}\) and SRO [001]o for θ-rotation and γ-rotation, respectively. θ and γ values are the angles between \(\overrightarrow{{{{\bf{B}}}}}\) and the surface normal of SRO films, i.e. SRO [110]o that appears to be the magnetic easy axis with the lowest coercive field (see Supplementary Note 5). The resulting FFT spectra of γ-rotation and θ-rotation for SRO film with t ≈ 17.6 nm and fields up to 14 T at T = 2.5 K are shown in the upper panel and lower panel, respectively, of Fig. 5c for angles ranging from 0o to 60o. As the angle increases from 0o to 60o, Fs1 gradually shifts to higher frequencies for both θ-rotation and γ-rotation. Figure 5d shows the θ and γ dependent quantum oscillations of dρ/d(μ0H) versus μ0H for SRO thin film with t ≈ 18.7 nm and fields up to 35 T at T = 0.3 K. For angles larger than about 30o, the bulk frequencies of F1–5 damp out rapidly as expected in thin films with increased surface scatterings. The extracted Fs1 as a function of γ and θ are summarized in Fig. 5e and f, respectively, where Fs1(5.5, 5) and Fs1(5.5, 4.5) are extracted from the oscillation periods of (1/μ0H5.5−1/μ0H5) and (1/μ0H5.5−1/μ0H4.5), respectively. We included the results for the SRO film with t ≈ 18.7 nm shown as diamond and downward-triangle symbols in Fig. 5e, f, which was measured with applied fields up to 35 T. However, we do note that, at some angles of around 30o, Fs1 in the FFT spectra seems to split into two frequencies but then merged into a single peak again at higher angles. Nevertheless, the extracted Fs1 values for all SRO films with different ts tend to follow the 1/cosθ or 1/cosγ dependence (red-dashed lines in Fig. 5e, f), indicating a 2D-like nature of the Fermi pocket for Fs1 (see Supplementary Note 6).
a The −d2σ/d(1/H)2 versus 1/μ0H at T = 2.5 K for SRO films with five different ts ranging from about 7.7 to 35.3 nm. The curves with different ts are shifted vertically for clarity. The corresponding FFT spectra are shown in (b). The oscillation and FFT amplitude for Fs1 appears to show a larger magnitude for ts in the range of about 10–20 nm. For t ≈ 17.6 nm, the angle-dependent FFT spectra for different γ and θ angles are shown in the upper panel and lower panel, respectively, in (c). For t ≈ 18.7 nm, the angle-dependent quantum oscillations of dρ/d(μ0H) versus μ0H up to 35 T were plotted in d, where the bulk frequencies of F1−5 damped out at angles larger than 30o. The curves with different θ and γ values are shifted vertically for clarity. The extracted Fs1 as a function of γ and θ angles are shown in e and f, respectively. The error bars were from the standard deviations of the extracted Fs1 values at each angle using various fitting schemes. The red dashed lines represent the 1/cosθ and 1/cosγ dependence. The inset cartoon in e illustrates the orientation for the γ and θ angles.
By taking the oscillation period of adjacent peaks and valleys in Fig. 5a for θ = 0o, the extracted Fs1 values as a function of the LL index n are shown in the upper panel of Fig. 6a for SRO films with t ≈ 13.7 and 17.6 nm. Here, n was determined by setting Bc as the field above which the quantum limit occurs. Fs1 marches down from about 34.5 T for n = 8.5–28 T for n = 4, and this behavior is consistent with the observed downward bending of the 1/μ0Hn−n curve in the Landau fan diagram shown in the lower panel of Fig. 6a. Surprisingly, the intercept n0, obtained by linearly extrapolating the high n data (black-dashed line), gives an unusual large phase shift of δ ≈ −2.0.
a The simulated curves based on the WOE formula with non-adiabatic correction are plotted and compared to the experimental data from SRO thin films with t ≈ 13.7 and 17.6 nm, where the color codes for the solid lines represent the α parameters ranging from 0 to 2.0 with a step of 0.2. The experimental data are found to fall between the simulated curves with α ≈ 1.2 and 1.4, exhibiting both a downward bending curvature in 1/μ0Hn−n curve and an unusually large phase shift n0 ≈ −2. b An illustration of the nonlocal cyclotron orbit resulting from WOE. c shows the deviation from linearity δ(1/μ0Hn) as a function of n due to non-adiabatic correction, which is in good agreement with the simulated curve with α = 1.3. The error bars for the experimental data were derived from the standard deviations in the extracted 1/μ0Hn values, which were error propagated to give the corresponding uncertainties for Fs1 and δ(1/μ0Hn). d The extracted Drude mean free path (ℓd) and the ratio of ℓd/t as a function of t, showing the largest ℓd/t for 10 < t < 20 nm. e The simulated 1/μ0Hn−n curves for α = 1.3 with different ts based on WOE, inferring an optimum thickness of about t ~ 10–20 nm for the dominant WOE in SRO thin films.
Discussions
The surface nature of Fs1 ≈ 30 T with a small effective mass m* = (0.30 ± 0.01)me was strongly supported by the 2D-like angle dependence of Fs1 and nonmonotonic t dependence of oscillation amplitude as shown in Figs. 5e, f and 3c, respectively. Considering a conventional 2D parabolic band with a frequency of 30 T, the field required for the quantum limit (Bq) can be calculated, giving Bq ≈ 30 and 15 T for spin-degenerate bands and single spin subband, respectively. We also remark that such a 2D Fermi pocket is not likely coming from the SRO/STO interface conduction due to band bending or oxygen loss in STO, which typically gives a larger effective mass of m* > 1.0me39,40. One intriguing possibility for such a 2D-like small pocket of Fs1 ≈ 30 T is then the unusual quantum oscillation due to WOE as illustrated in Fig. 6b, which is supported by the existence of nonoverlapping Weyl-node pairs near the Fermi energy from our band calculations (Fig. 4) and also several earlier reports20,24. The dashed circles around the projected Weyl nodes with a length scale of inverse magnetic length (\({\ell }_{{{{\rm{B}}}}}^{-1}\)) are boundaries where the transition from the Fermi-arc surface states to the bulk states happens before reaching the ends of the Fermi-arcs, giving rise to a reduced effective area for the Weyl-orbit and thus the non-adiabatic correction effect12. The quantum oscillation due to WOE can be described as12
where n is the LL index, μ is the chemical potential, and υ is the Fermi velocity. \({k}_{0}^{{\prime} }\equiv {k}_{0}(1-4\alpha /{k}_{0}{\ell }_{{{{\rm{B}}}}})\) is defined as the effective wave vector connecting the projected Weyl-node pair on the surface, and k0 is the length of the Fermi-arc. \({\ell }_{{{{\rm{B}}}}}\equiv \sqrt{\hslash /e{\mu }_{0}{H}_{n}}\) is the magnetic length, and α is the parameter governing the non-adiabatic correction12. The corresponding frequency can then be calculated using Fs1 = 1/μ0Hn−1/μ0Hn−1. One important consequence of Eq. (1) is the thickness dependence of the phase in the oscillation. The 1/μ0Hn value will progressively decrease with increasing t values, and the amount of phase shift should be independent of n, which is in accordance with our observation shown in Fig. 5a. We remark that the phase shift due to trivial minor carrier density variations is expected to be linearly proportional to n, which is thus strikingly different from the n-independent phase shift due to WOE (see Supplementary Note 7). By solving for 1/μ0Hn in Eq. (1), the resulting simulated Fs1−n and 1/μ0Hn−n curves are shown as solid lines in the upper panel and lower panel of Fig. 6a, respectively, where the gradual change of line color represents the progressive increase of α parameter from 0 to 2. Here, we used m* = 0.3me, t = 13.7 nm, and Fs1 = 40 T for α = 0.
For α = 0, Fs1 is independent of n, and the 1/μ0Hn−n curve is strictly linear with an intercept of n0 ≈ 0.76. When taking into account the non-adiabatic correction effect (α ≠ 0), several notable variations occur. First, the overall Fs1 values shift to lower values, and the resulting Fs1−n curves show a concave downward feature, where Fs1 values decrease with decreasing n. Secondly, the 1/μ0Hn−n curve in the Landau fan diagram also shows gradual upward-shifting with increasing concave downward curvature as α increases. We note that the concave downward curvature in the 1/μ0Hn−n curve is distinct from the behavior due to the Zeeman energy contribution that causes a concave upward curvature instead13. The experimental data of Fs1 and 1/μ0Hn are shown as downward triangles and upward triangles in Fig. 6a for t ≈ 13.7 and 17.6 nm, respectively, which turns out to agree well with the simulated curves with α ≈ 1.3. The amount of deviation δ(1/μ0Hn) from linearity with respect to that for n ≥ 8 is shown in Fig. 6c, where the slope of the linear background derives from the 1/μ0Hn curve for α = 0. The simulated curve of δ(1/μ0Hn)−n (red dashed line in Fig. 6c) with α = 1.3 shows quantitative agreements with the experimental data for SRO films with t ≈ 13.7 and 17.6 nm. We note that the simulated curves for different α were calculated solely from Eq. (1) without imposing additional scaling parameters (see Supplementary Note 7). Once α = 1.3 is determined, the corresponding WOE parameters can then be calculated, giving k0 = 1.09 nm−1, μ = 15.43 meV, and υ = 1.34 × 105 m s−1. The extracted k0 value falls in the same order of magnitude as the calculated k0 as shown in Fig. 4d. We also note that there can be multiple Weyl-node pairs on (110)o plane that support for multiple Weyl-orbits with different frequencies, such as Fs2. However, due to the small oscillation amplitude for Fs2, it is not possible to resolve its intrinsic mechanism with current data. In particular, we remark that the non-adiabatic correction effect, i.e. a finite α, can, in principle, shift the 1/μ0Hn−n curve in the Landau fan diagram, resulting in a significant change in the intercept n0. Therefore, an unusually large phase shift of δ ≈ −2.0 is possible for the WOE with the non-adiabatic correction, which can be another unusual feature for quantum oscillations deriving from WOE.
In general, the phase shift of the ρ oscillations in a 2D system can be expressed as δ = \(\frac{1}{2}+\frac{{\phi }_{{{{\rm{B}}}}}}{2\pi }\) (modulo 1), where ϕB is the Berry phase, and the magnitude of δ is not likely to exceed 1.0. On the other hand, the phase shift of quantum oscillations from a simple 3D bulk Weyl-node should give a δ close to ±1/85,8,9. It was pointed out theoretically9 that a large anomalous phase shift can occur in a 3D topological WSM when the Fermi level is close to the Lifshitz point at which both the linear and parabolic bands are important. According to theory9, the model Hamiltonian can be expressed as \({{{\mathcal{H}}}}\) = A(kxσx + kyσy)+M (\({k}_{{{{\rm{w}}}}}^{2}-{k}^{2}\)), where A and M are the coefficients for the linear and parabolic band, respectively. kw is the separation of the Weyl-node pair. Two energy scales of EA ≡ Akw/2 and \({E}_{{{{\rm{M}}}}}\equiv M{k}_{{{{\rm{w}}}}}^{2}/4\) govern the phase shift behavior, where an anomalous large phase shift appears for EA ≤ EM. By using the parameters from our quantum oscillation data of Fs1, EA, and EM are estimated to be about 48.5 and 2.3 meV, respectively, where we used kw = k0 and an effective mass of 5me for the parabolic band. Therefore, the observed quantum oscillations in our SRO films do not fall in the condition for the large anomalous phase shift due to the coexistence of the linear and parabolic bands.
In a Weyl metal, the observed quantum oscillations can derive from complex competitions among several different mechanisms, such as the WOE, 3D Weyl nodes, and 3D bulk pockets. In our SRO thin films, the quantum oscillation of Fs1 we observed for t ≤ 40 nm is not likely dominated by 3D Weyl-node bulk states, since its amplitude shows nonmonotonic variation with t (lower-panel of Fig. 3c), and also its angle dependence behaves closer to a 2D-like Fermi surface (Fig. 5e, f). On the other hand, the occurrence of quantum oscillations due to WOE requires a high uniformity of film thickness and also t ≪ ℓd, which are both well satisfied in our SRO films as shown in Fig. 1 and Table 1. Phenomenologically, the oscillation amplitude of WOE is expected to be proportional to exp(−t/ℓd)13. The ratio of ℓd/t versus t in SRO thin films is well above 3 for t < 40 nm and attends maximum values for 10 ≤ t ≤ 20 nm as shown in Fig. 6d, inferring an optimum thickness range for a maximum oscillation amplitude due to WOE. In addition, the condition of ℓd/t ≥ 3 also supports for observed rapid damping of the bulk frequencies of F1–5 due to the increased surface scattering for angles larger than 30o as shown in Fig. 5d. On the other hand, we also simulated the t dependence of 1/μ0Hn−n curves with α = 1.3 as demonstrated in Fig. 6e, where an unusually large phase shift of n0 ~ −2 can only be observed for t ≤ 20 nm. As t increases to 50 nm or larger, the 1/μ0Hn-n curve shifts downward to smaller values of 1/μ0Hn, and thus a much higher field strength is required to access the low n states, posing an inevitable limitation on the lowest n that can be reached by available field strength. In other words, for t > 50 nm, the WOE amplitude and field accessible range in n are both reduced, and the contribution from 3D bulk pockets may become dominant instead, making it difficult to identify the quantum oscillations due to WOE.
At last, the observed Bc ~ 15 T is not the saturation field (Bsat ≡ (ℏkFk0/πe)) for the WOE. For μ0H ≥ Bsat, the Weyl orbit mostly happens within the bulk states, and thus the associated quantum oscillations vanish12,13. Using the extracted parameters in our SRO films, Bsat is estimated to be about 80 T and >Bc. In a recently reported quantum oscillations data in SRO films41, a similar 2D-like small Fermi pocket with a frequency of 30 T was reported and attributed to Fermi-arc surface states. Nevertheless, the discussions in our work are focused on the untwinned SRO film thickness regime with t < ℓd, particularly for t in a range from 10 to 20 nm, and the effect of non-adiabatic correction turns out to be an important ingredient to explain the observed features in Weyl-orbit quantum oscillations. However, precise identification of the quantum limit regime for Fs1 is challenging and may call for further investigations, which requires a careful and precise extraction of Fs1 contribution from a large oscillating background (F1−5) that grows rapidly with field strength as shown in Fig. 6b (see Supplementary Note 8).
In summary, the revelation of quantum oscillations due to WOE in Dirac and Weyl systems is challenging due to the mixing of quantum oscillations from 3D bulk Fermi pockets. Combining quantum oscillation measurements in SRO thin films and WOE simulations, we identified an optimum thickness of t ~ 10−20 nm for achieving a dominant WOE contribution, where several unusual features associated with WOE were clearly observed. Starting from the growth of a series of untwinned SRO films on miscut STO (001) substrates with different ts by using an adsorption-controlled growth technique with an oxide MBE, the RRR (ρ(2.5 K)) shows a progressive increase (decrease) with film thicknesses ranging from 7.7 to 35.3 nm, and the condition of t < ℓd is always satisfied to favor the bulk tunneling and thus WOE, where the measurement geometry was kept the same with respect to the SRO orthorhombic crystalline direction. The calculated band structure of SRO shows complex band crossings and supports for the existence of nonoverlapping Weyl nodes when projecting on the film surface plane. The observed H-linear transverse MR with fields up to 35 T and also negative longitudinal MR in our SRO films further support its topological Weyl metal phase. From the rigorous angle and thickness-dependent measurements of quantum oscillations with fields up to 35 T, we revealed an unusual quantum oscillation with a small frequency of Fs1 ≈ 30 T, which behaves like a 2D Fermi pocket with a small effective mass of about 0.3me. Its oscillation amplitude shows nonmonotonic t-dependence and attends a maximum when t is in the range of 10–20 nm, where a systematic phase shift of the oscillation with t was observed. In addition, the extracted 1/μ0Hn−n curve in the Landau fan diagram shows an unusual concave downward curvature. Those observations agree well with the WOE formalism with non-adiabatic corrections, corresponding to a Fermi-arc length (k0) of 1.09 nm−1 and a non-adiabatic correction parameter (α) of about 1.3. With excellent control on the growth of highly crystalline and untwinned oxide thin films, the topological Weyl metal SRO can be an ideal platform to explore the exotic phenomena associated with the bulk Weyl nodes and Fermi-arc surface states.
Methods
SRO thin film growths
The adsorption-controlled growth of SRO thin films was carried out using an oxide MBE system. The detailed growth conditions and structural characterization were reported in an earlier paper26. For SRO films with t ≈ 9, 13.7, and 18.7 nm, the magnetotransport measurements with applied fields up to 35 T were carried out at High Field Magnet Laboratory in Nijmegen. For other ts and another t ≈ 13.7 nm of the same batch, the magnetotransport measurements were performed using a superconducting magnet with fields up to 14 T. The high-resolution X-ray measurements were performed at TPS 09A and TLS 07A of the NSRRC in Taiwan, where the orthorhombic phase, film thicknesses, and orientation of the SRO films were carefully examined (see Supplementary Note 1). The surface roughness of SRO films and the STO substrate miscut orientation were measured by an AFM. The SRO films presented in this work were carefully selected to have the same STO miscut orientation with respect to the direction of the probing currents for the magnetotransport measurements, i.e. the current direction is perpendicular to the terrace edge of the STO (001) substrate.
Band calculations
The DFT + U calculations were performed with full potential linear augmented plane waves plus local orbitals (FP-LAPW + lo) and the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) provided in the WIEN2k code.32,33 For the treatment of Hubbard U terms, we have adopted the self-interaction corrections developed by Anisimov et al.34 which is available as a SIC scheme in the WIEN2k package. We have used the crystal lattice constants of a0 = 5.584 Å, b0 = 5.540 Å, and c0 = 7.810 Å, which were determined by high-resolution X-ray measurements on our samples, and a k-mesh of 22 × 22 × 15 was used to sample the Brillouin zone. We have performed calculations with several different values of U with J fixed to be J = 0.2U. All the DFT + U calculations were done with the inclusion of spin-orbit coupling on the heavy atoms of Sr and Ru.
The tight-binding model employed for the calculation of Weyl nodes was composed of the d-orbitals of the Ru atoms as well as the p orbitals of the O atoms, and the hopping parameters are determined by fitting the DFT band structure using the Wannier9035. We focused on five bands near the Fermi energy, as shown in Fig. 6a of the main text. We searched for all the band crossings residing in four pairs of bands out of these five bands. These four pairs are defined as: pair I → green band and the one below; pair II → (green, red); pair III → (red, blue); pair IV → (blue, pink). Finally, we confirmed the Weyl nodes by calculating the chirality of each band crossing using the WannierTools36.
The Fermi surfaces are plotted using the spectral function which is defined as
where \({\hat{H}}_{{{{\rm{TB}}}}}(\overrightarrow{{{{\bf{k}}}}})\) is the tight-binding model fitted by the Wannier90, and we have used the codes provided by WannierTools36 for evaluating the spectral function.
Data availability
All the supporting data are included in the main text and also in Supplementary information. The raw data and other related data for this paper can be requested from W.L.L.
Code availability
The input files for DFT calculations using WIEN2k are available upon request.
References
Shoenberg, D. Magnetic Oscillations in Metals. Cambridge Monographs on Physics (Cambridge University Press, 1984).
Lifshitz, I. & Kosevich, A. Theory of magnetic susceptibility in metals at low temperatures. Sov. Phys. JETP 2, 636 (1956).
Onsager, L. Interpretation of the de Haas–van Alphen effect. Lond. Edinb. Dubl. Philos. Mag. 43, 1006–1008 (1952).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
He, L. P. et al. Quantum transport evidence for the three-dimensional Dirac semimetal phase in Cd3As2. Phys. Rev. Lett. 113, 246402 (2014).
Arnold, F. et al. Chiral Weyl pockets and Fermi surface topology of the Weyl semimetal TaAs. Phys. Rev. Lett. 117, 146401 (2016).
Xiong, J. et al. High-field Shubnikov–de Haas oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 86, 045314 (2012).
Wang, C. M., Lu, H.-Z. & Shen, S.-Q. Anomalous phase shift of quantum oscillations in 3D topological semimetals. Phys. Rev. Lett. 117, 077201 (2016).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Huang, S.-M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Potter, A. C., Kimchi, I. & Vishwanath, A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nat. Commun. 5, 5161 (2014).
Moll, P. J. W. et al. Transport evidence for Fermi-arc-mediated chirality transfer in the Dirac semimetal Cd3As2. Nature 535, 266–270 (2016).
Zhang, C. et al. Evolution of Weyl orbit and quantum Hall effect in Dirac semimetal Cd3As2. Nat. Commun. 8, 1272 (2017).
Nishihaya, S. et al. Quantized surface transport in topological Dirac semimetal films. Nat. Commun. 10, 2564 (2019).
Galletti, L., Schumann, T., Kealhofer, D. A., Goyal, M. & Stemmer, S. Absence of signatures of Weyl orbits in the thickness dependence of quantum transport in cadmium arsenide. Phys. Rev. B 99, 201401 (2019).
Horio, M. et al. Electronic reconstruction forming a C2-symmetric Dirac semimetal in Ca3Ru2O7. npj Quantum Mater. 6, 29 (2021).
Kreisel, A. et al. Quasi-particle interference of the van Hove singularity in Sr2RuO4. npj Quantum Mater. 6, 100 (2021).
Koster, G. et al. Structure, physical properties, and applications of SrRuO3 thin films. Rev. Mod. Phys. 84, 253–298 (2012).
Chen, Y., Bergman, D. L. & Burkov, A. A. Weyl fermions and the anomalous Hall effect in metallic ferromagnets. Phys. Rev. B 88, 125110 (2013).
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).
Itoh, S. et al. Weyl fermions and spin dynamics of metallic ferromagnet SrRuO3. Nat. Commun. 7, 11788 (2016).
Mackenzie, A. P. et al. Observation of quantum oscillations in the electrical resistivity of SrRuO3. Phys. Rev. B 58, R13318–R13321 (1998).
Takiguchi, K. et al. Quantum transport evidence of Weyl fermions in an epitaxial ferromagnetic oxide. Nat. Commun. 11, 4969 (2020).
Nair, H. P. et al. Synthesis science of SrRuO3 and CaRuO3 epitaxial films with high residual resistivity ratios. APL Mater. 6, 046101 (2018).
Kar, U. et al. High-sensitivity of initial SrO growth on the residual resistivity in epitaxial thin films of SrRuO3 on SrTiO3 (001). Sci. Rep. 11, 16070 (2021).
Chang, S. H. et al. Thickness-dependent structural phase transition of strained SrRuO3 ultrathin films: the role of octahedral tilt. Phys. Rev. B 84, 104101 (2011).
Gan, Q., Rao, R. A. & Eom, C. B. Control of the growth and domain structure of epitaxial SrRuO3 thin films by vicinal (001) SrTiO3 substrates. Appl. Phys. Lett. 70, 1962–1964 (1997).
Capogna, L. et al. Sensitivity to disorder of the metallic state in the ruthenates. Phys. Rev. Lett. 88, 076602 (2002).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Zhang, C.-L. et al. Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 7, 10735 (2016).
Schwarz, K. & Blaha, P. Solid state calculations using WIEN2k. Comput. Mater. Sci. 28, 259–273 (2003).
Blaha, P. et al. WIEN2k: an APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).
Anisimov, V. I., Solovyev, I. V., Korotin, M. A., Czyżyk, M. T. & Sawatzky, G. A. Density-functional theory and NiO photoemission spectra. Phys. Rev. B 48, 16929–16934 (1993).
Mostofi, A. A. et al. An updated version of wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. Wanniertools : an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Jeng, H.-T., Lin, S.-H. & Hsue, C.-S. Orbital ordering and Jahn–Teller distortion in perovskite ruthenate SrRuO3. Phys. Rev. Lett. 97, 067002 (2006).
Shai, D. E. et al. Quasiparticle mass enhancement and temperature dependence of the electronic structure of ferromagnetic SrRuO3 thin films. Phys. Rev. Lett. 110, 087004 (2013).
Kozuka, Y. et al. Two-dimensional normal-state quantum oscillations in a superconducting heterostructure. Nature 462, 487–490 (2009).
Wang, Z. et al. Tailoring the nature and strength of electron–phonon interactions in the SrTiO3(001) 2D electron liquid. Nat. Mater. 15, 835–839 (2016).
Kaneta-Takada, S. et al. High-mobility two-dimensional carriers from surface Fermi arcs in magnetic Weyl semimetal films. npj Quantum Mater. 7, 102 (2022).
Acknowledgements
We thank A.P. Mackenzie, N.P. Ong, Y. Matsuda, J. Checkelsky, M. Hirschberger, M. Orlita, and L. Balicas for valuable and fruitful discussions. This work was supported by Academia Sinica (Thematic Research Program), National Science and Technology Council of Taiwan (NSTC Grant Nos. 108-2628-M-001 -007 -MY3 and 106-2112-M-213-006-MY3), and HFML-RU/NWO-I, a member of the European Magnetic Field Laboratory (EMFL).
Author information
Authors and Affiliations
Contributions
U.K., Chih-Yu Lin, B.D., C.-T.C., and W.-L.L. carried out the low-temperature magneto-transport measurements and data analyses. U.K. and A.K.S. grew the epitaxial SRO films. Y.-T.H., M.B., and S.W. performed magnetotransport measurements at HMFL in Nijmegen. A.K.S., S.Y., Chun-Yen Lin, and C.-H.H. performed the X-ray measurements at NSRRC in Taiwan. W.-C.L. performed SRO band calculations. S.W., W.-C.L., and W.-L.L. designed the experiment and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kar, U., Singh, A.K., Hsu, YT. et al. The thickness dependence of quantum oscillations in ferromagnetic Weyl metal SrRuO3. npj Quantum Mater. 8, 8 (2023). https://doi.org/10.1038/s41535-023-00540-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-023-00540-3
This article is cited by
-
Magnetism and berry phase manipulation in an emergent structure of perovskite ruthenate by (111) strain engineering
npj Quantum Materials (2023)