Abstract
Geometrical aspects of electronic states in condensed matter have led to the experimental realization of enhanced electromagnetic phenomena, as exemplified by the giant anomalous Hall effect (AHE) in topological semimetals. However, the guideline to the large AHE is still immature due to lack of profound understanding of the sources of the Berry curvature in actual electronic structures; the main focus has concentrated only on the band crossings near the Fermi level. Here, we show that the band crossings and flat bands cooperatively produce the large intrinsic AHE in ferromagnetic nodal line semimetal candidate Fe3GeTe2. The terahertz and infrared magneto-optical spectroscopy reveals that two explicit resonance structures in the optical Hall conductivity spectra σxy(ω) are closely related to the AHE. The first-principles calculation suggests that both the flat bands having large density of states (DOS) and the band crossings near the Fermi level are the main causes of these Hall resonances. Our findings unveil a mechanism to enhance the AHE based on the flat bands, which gives insights into the topological material design.
Similar content being viewed by others
Introduction
Quantum geometric phase of electronic states, namely Berry phase, often plays a decisive role in the transport and optical phenomena1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. The intrinsic AHE derived from the electronic band structure is the most representative example, where the anomalous Hall (AH) conductivity is described by the Berry curvature in the momentum space1,2. It has been well established that the band crossings produce large Berry curvature, therefore the topological electronic structures such as the Dirac/Weyl points and nodal lines significantly contribute to the intrinsic AHE1,2,3,4,5,6,7,8,9,10,11,12,13. In fact, the giant AHE has been observed for the topological semimetals such as Co3Sn2S27,8 and Co2MnGa9,10, where the Hall conductivity and the tangent of Hall angle simultaneously exceed 500 Ω−1cm−1 and 0.1, respectively. In recent years, much theoretical effort based on the first-principles calculations has been made to analyze and design the topological electronic structure exhibiting intriguing quantum transport phenomena of Berry phase origin1,2,3,4,5,6,7,8,9,10,11,12,13,16. However, the theoretical suggestion towards the large AHE have been hardly addressed partly because the direct correspondence between the actual electronic structure and AHE has rarely been explored experimentally. It is imperative to discuss the band-resolved contributions to the AHE for comprehensive understanding.
Here, we study the large AHE in the ferromagnetic van der Waals (vdW) semimetal Fe3GeTe2 thin film using the broadband magneto-optical spectroscopy. Since the intrinsic AHE exhibits the strong correlation with the band structure, the optical AHE, i.e., the energy-dependent AH conductivity, provides the direct information on the electronic structure associated with the intrinsic AHE12,17,18,19; the resonantly enhanced optical AHE manifests the presence of band structures producing the AHE, which uncovers the main source of the Berry curvature.
We target the recently discovered prospective nodal line semimetal Fe3GeTe2 that exhibits the large AHE comparable to other topological semimetals5,7,8,9,10,11 and two-dimensional ferromagnetism20,21,22,23,24,25,26,27,28. It has a layered hexagonal crystal structure belonging to the space group P63/mmc (Fig. 1a). There are two inequivalent Fe sites, FeI and FeII. The FeI-FeI dumbbell penetrates the center of each hexagon of the honeycomb lattice formed by FeII and Ge atoms. FeII-Ge honeycomb lattice is sandwiched by two Te layers coupled via the vdW force and stacked in the so-called AB bilayer configuration. The band structure calculation based on the density functional theory (DFT) suggests the presence of the topological nodal lines along the KH line in the Brillouin zone protected by crystalline symmetries in the case without the spin-orbit coupling (SOC) (Fig. 1b; upper panel of Fig. 1c)11. When the SOC is introduced, these nodal lines open gaps as indicated by red and blue curves in Fig. 1d (lower panel of Fig. 1c), which should generate the Berry curvature11. The flat bands are also discerned as exemplified by green curves in Fig. 1d, some of which are suggested to be crucial for the two-dimensional ferromagnetism20,26 and can be the sources of the large Berry curvature. So far, only the Berry curvature generated by the nodal lines has been considered to cause the large AHE.
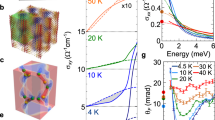
a Crystal structure of Fe3GeTe2 (left panel). The right upper and right lower panels illustrate the top view and honeycomb structure, respectively. b Brillouin zone of Fe3GeTe2 with the high symmetry points. c Schematic illustration of the nodal line structure along KH line (upper panel). The spin orbit coupling (SOC) lifts the degeneracy along the nodal line structure, resulting in the gap opening (lower panel). d The band structure with considering the SOC along KM, KΓ and KH lines. The red and blue curves represent the bands composing the nodal line near the Fermi level. The green curves are examples of the flat bands. e Temperature dependence of the longitudinal conductivity (red line) and Hall conductivity when cooled in the magnetic field of 70 mT (blue line). f Magnetic-field dependence of the Hall conductivity at various temperatures for the magnetic field parallel to the c axis.
Results and discussion
Magneto-transport properties
Figure 1e, f summarizes the electrical transport properties of a (001)-oriented 20-nm-thick epitaxial thin film of Fe3GeTe2 studied here (for more details of thin film growth, see Methods). The longitudinal conductivity σxx shows a metallic behavior in a wide temperature region ranging from 20 to 300 K but slightly decreases below 20 K (Fig. 1e), which is observed also for the bulk crystals and thin flakes20,21,23,25. The Hall conductivity σxy steeply develops below the ferromagnetic transition temperature TC ~ 240 K (Fig. 1e)21,22, which shows the clear hysteresis in the magnetic-field dependence owing to the perpendicular ferromagnetic anisotropy (Fig. 1f). The Hall conductivity and the tangent of Hall angle at 2 K reach ~100 Ω−1cm−1 and ~0.04, respectively. These anomalous Hall responses are comparable to those of the thin flakes23,27 and larger than those of other thin films fabricated by molecular beam epitaxy25,28 (see also Supplementary Note 1).
Optical conductivity spectra
Figure 2a, b show the longitudinal optical conductivity spectra σxx(ω) at 20 K in terahertz (1–8 meV) and infrared (0.1–2.0 eV) regions, respectively. In the terahertz region, Re σxx(ω) is as large as the dc value with flat energy dependence, while Im σxx(ω) is almost zero (Fig. 2a). This observation indicates that the scattering time τ is shorter than the time scale of picosecond, given that the intraband Drude response of the free carriers dominates the spectra in the terahertz region. On the other hand, the interband transitions including those for the nodal lines can be observed in the infrared region (Fig. 2b). Re σxx(ω) and Im σxx(ω) show gradual decrease and increase, respectively, towards the low energy (Fig. 2b), which are reasonably connected to the terahertz spectra. The presently observed σxx(ω) spectrum is qualitatively consistent with the first-principles calculation (Supplementary Fig. 1).
The longitudinal optical conductivity spectra σxx(ω) at 20 K in the terahertz a and the mid-to-near infrared b regions. The terahertz Faraday rotation θF c and ellipticity ηF d spectra at various temperatures. The error bars in c indicate the standard deviation. The inset of d shows the schematic illustration of the Faraday rotation measurement. The infrared Kerr rotation θK e spectra and ellipticity ηK f spectra at various temperatures. The inset of e shows the schematic illustration of the Kerr rotation measurement.
Magneto-optical effects
To explore the optical transitions related to the AHE, we measure the Faraday rotation spectra in the terahertz region (1–8 meV) and the Kerr rotation spectra in the mid-to-near infrared region (0.1–1.5 eV). These magneto-optical measurements are performed at zero field for the single ferromagnetic domain (see Methods and Supplementary Fig. 2). Figure 2c, d shows the temperature dependence of the Faraday rotation θF and ellipticity ηF spectra in the terahertz region, respectively. The magnitude of the Faraday rotation θF increases below TC with decreasing the temperature and tends to be saturated around 70 K, which is proportional to the AH conductivity (Supplementary Fig. 3a). On the other hand, the ellipticity ηF spectra are close to zero at all temperatures, indicating the absence of electronic transition associated with the AHE in the terahertz region (<8 meV). In contrast, the mid-infrared Kerr rotation θK and ellipticity ηK show the clear resonance structures below TC (Fig. 2e, f; see also Supplementary Fig. 3b). The infrared Kerr rotation spectra θK (Fig. 2e) have the gradual decrease below 1.1 eV towards the lower energy with the hump-like structure at 0.6 eV. The Kerr ellipticity spectra ηK (Fig. 2f) show two broad dip structures centered at 0.25 eV and 0.7 eV as indicated by the black arrows, which reflect the presence of dominant interband transitions leading to the large intrinsic AHE as discussed below.
Optical Hall conductivity spectra
We can quantitatively evaluate the role of these electronic transitions by exploiting the complex Hall conductivity spectra σxy(ω) deduced from the optical conductivity σxx(ω) and magneto-optical spectra (Fig. 3; see also Methods). In the infrared region, Re σxy(ω) shows peak and dip structures at 0.6 eV and 1.2 eV, respectively, and further increases below 0.3 eV towards the low energy (Fig. 3c), which is reasonably connected to the terahertz spectra and dc AH conductivity (Fig. 3a). On the other hand, in Im σxy(ω), two resonance structures are observed at 0.2 eV and 0.7 eV, as indicated by the circle and triangle in Fig. 3d, respectively. Im σxy(ω) converges to zero in the terahertz region in accord with the causality constraint as Im σxy(ω = 0) = 0 (Fig. 3b). In general, the resonance structure in Im σxy(ω) indicates the existence of optical transition associated with the AHE, while the Re σxy(ω) shows the dispersive spectra around the resonance energy and leads to the dc AH conductivity at ω = 012,17,18,19. Accordingly, the observed resonances in Im σxy(ω) demonstrate the presence of two distinct interband transitions closely relevant to the dc AHE, evidencing its intrinsic origin. Since both resonances at 0.2 eV and 0.7 eV have the same sign, these transitions cooperatively enhance the dc AHE. It is to be noted here that the broad spectral distribution of Im σxy(ω) (Fig. 3d) spreading over 1.2 eV is never expected for the extrinsic AHE induced by the intraband scattering, which would show up in the low-energy Drude response region below ħτ−1, if any.
The real a and imaginary b parts of the terahertz Hall conductivity spectra σxy(ω) at 20 K. c The real part of the experimental (red solid curve) and calculated (red dotted curve) optical Hall conductivity spectra σxy(ω) in the infrared region. d The imaginary part of the experimental (blue solid curve) and calculated (blue dotted curve) optical Hall conductivity spectra σxy(ω) in the infrared region. The green solid curves display the calculated σxy(ω) when considering only six bands composing the nodal lines (red lines in Fig. 4c). The orange solid curves show the calculated σxy(ω) when considering the optical transition from the bands located at −0.8 – −0.5 eV which include the flat bands around −0.65 eV (orange regions in Fig. 4b, c). All the calculated spectra are multiplied by a factor of 1/8 for comparison. The red and blue squares at zero energy in (a-d) represents the dc Hall conductivities at 0 T acquired from the transport measurements.
The sum rule for the optical Hall conductivity further corroborates the dominant roles of these two resonances in the dc AH conductivity. The Kramers–Kronig relation for Re σxy(ω = 0) and Im σxy(ω) yields the sum rule29;
Namely, the dc AH conductivity is given by the integral of the imaginary part divided by ω. Here, we define the spectral weight Sxy(ωc) as
where ωc is the cutoff energy and ωmin is the low-energy edge of the magneto-optical measurement (ωmin = 0.1 eV). Sxy(ωc) thus represents the contribution to the dc AHE from the optical transitions between ωmin and ωc (green line, Fig. 4a; see also Supplementary Fig. 4). Sxy(ωc) increases with ωc and tends to saturate at around 1.2 eV; Sxy(ωc) at the high-energy edge (2.2 eV) approaches 80 % of the dc Hall conductivity, which demonstrates that the two resonance structures below 1.2 eV (circle and triangle in Fig. 3d) are the main sources of the dc AHE. It should be emphasized that, although there exist the large peak structures above 1.2 eV (Fig. 4a), their contributions to the dc value Re σxy(ω = 0) are reduced by the factor of ω in the denominator of Eq. (1). The extrinsic mechanism for AHE arising, e.g., arising from the skew scattering of conduction electrons1, may show up only in the photon energy range of the Drude response below 10 meV, while such an extrinsic origin of the AHE has not been reported in this material11,27.
a The spectral weight Sxy(ωc) (green solid curve) and Im σxy(ω) spectra (light blue curve) up to 2.2 eV (see the main text for the definition of Sxy(ωc)). The dc AH conductivity at 20 K, 0 T (σxy(0)) is indicated by the square at ωc = 0 and dashed green horizontal line. b The calculated DOS. The transition indicated by the triangle is ascribed to the higher-lying resonance observed in Figs. 3d and 4a. The shaded regions in orange and blue denote the large DOS due to the flat bands, some of which are also indicated by the green curve in Fig. 1d. c The band structure with the SOC. Red curves represent six bands composing the nodal lines around Fermi level. d The real part of the optical Hall conductance spectra σxy(ω) calculated for a two-dimensional single band-crossing point for various Fermi level μ (see Supplementary Note 3).
Comparison with the first-principles calculation
To elucidate the origins of two resonance structures, we calculate the σxy(ω) spectra with the DFT (red and blue dotted curves in Fig. 3c, d). The theoretical spectra show the peak structure at 0.4 eV with a shallow dip at 1.2 eV in Re σxy(ω), and the broad peak at 0.7 eV in Im σxy(ω). While many fine structures in the theoretical spectra are discerned as compared to the experimental spectra partly because of the small damping constant (smearing parameter) η assumed in Eq. (12) (see Methods), the overall features of theoretical spectra are consistent with the experimental spectra at least above 0.3 eV dominated by the resonance structure marked by the triangle in Fig. 3d. This broad peak structure centered at 0.7 eV is ascribed to the optical transition between the flat bands with the large DOS: The sharp peak located at −0.65 eV and the broad band ranging from 0.05 eV to 0.55 eV are observed in the energy dependence of the DOS (Fig. 4b), which are shaded in orange and blue, respectively, in Fig. 4b, c. Correspondingly, the flat (or less dispersive) bands are concentrated in these regions, as exemplified by the green curves in Fig. 1d. The flat bands near −0.65 eV were confirmed by the previous ARPES measurement11,26, while those from 0.05 to 0.55 eV are considered to be responsible for gate-tunable room-temperature ferromagnetism20. To evaluate the contribution from the flat bands around −0.65 eV more directly, we calculate the σxy(ω) spectra when the initial state of the optical transition is limited to the bands located from −0.8 to −0.5 eV which include the flat bands as highlighted by orange in Fig. 4c. The resultant σxy(ω) (orange curves in Fig. 3c, d) makes a significant contribution to the higher-lying resonance and leads to almost half of the total dc AH conductivity as indicated by the lowermost energy value, i.e., Re σxy(ω = 0) (see red and orange circles at zero frequency in Fig. 3c). These facts demonstrate the important role of the flat bands in the AHE. We also confirm that the flat bands around −0.65 eV host the large Berry curvature on the basis of the calculated Fermi-level dependence of the AH conductivity (Supplementary Fig. 5).
Below 0.3 eV, the experimental and theoretical results show the different trend (Fig. 3c, d). While the experimental Im σxy(ω) has a positive peak as indicated by the circle in Fig. 3d, the theoretical one has a negative peak. This observation indicates that the low-energy transitions are not well reproduced within the DFT level perhaps because of the underestimated electron-correlation effect, which plays some roles in the electronic structure of this material as pointed out in the previous studies11,26 (for more detailed discussion, see Supplementary Note 2). Nevertheless, the band calculation and previous ARPES measurement suggest the existence of abundant (anti-)crossing points and nodal lines near the Fermi level (Fig. 4c)11, which are responsible for the optical transitions in this energy region. On the basis of the theoretical model assuming the two-dimensional single anti-crossing point, the interband transition near the anti-crossing point causes the resonance peak at the double of the energy distance between the anti-crossing point and Fermi level (Fig. 4d; see also Supplementary Note 3)17,18,30. The resonance in σxy(ω) as well as dc value σxy(0) is enhanced when the Fermi level is close to the anti-crossing point. In the present material, the superposition of these node structures located at the different energy positions presumably produces the broad peak structure as observed experimentally. The calculated σxy(ω) for six bands composing the nodal lines (red lines in Fig. 4c) possesses the resonance structure around 0.1 eV (Fig. 3c, d), so that part of spectral weight in lower-lying peak stems from the nodal lines.
As indicated by Fig. 4a, the broad optical transition centered at 0.7 eV is found to have the significant impact on the dc transport due to the large DOS, contrary to the general trend that the higher-lying resonance loses the weight for the dc AHE as suggested by the sum rule (Eq. (1)). In fact, this energy scale is relatively large compared with the cases for SrRuO312,18 and Co3Sn2S219, where the optical transitions below ~0.3 eV are dominant for the AHE. These observations suggest the importance of the flat band, or more generally, the large DOS for enhancing the AH conductivity (see also Supplementary Note 4). The relatively high transition energy among the flat bands provides the robust AH conductivity against the subtle change of the Fermi level. This character is distinguished from the transitions relating to the crossing points around the Fermi level as shown in Fig. 4d.
The present experimental and theoretical spectroscopies reveal that two distinct band structures, i.e., the flat bands with the large DOS and the band crossings near the Fermi level, cooperatively produce the large intrinsic AHE. In addition to the widely recognized importance of the topological nodes, our results show the significant impact of the flat band for the topological electromagnetic phenomena. The flat band becomes known to be ubiquitous for many systems including kagome-lattice materials and vdW twisted bilayer heterostructures, while the study of its electromagnetic response has just launched31,32,33,34. Our findings may provide a base of research for exploring various enhanced topological phenomena including the anomalous Nernst effect and nonlinear optical effects on such emerging systems, paving a way for the future optical/electrical applications.
Methods
Thin film fabrication
The Fe3GeTe2 thin film was fabricated with the ~2-nm-thick (Bi,Sb)2Te3 buffer layer on a semi-insulating InP(111)A substrate by molecular beam epitaxy technique. The Fe3GeTe2 and buffer layer were grown at 380 °C at a base vacuum pressure of ~1 × 10–7 Pa. All fluxes were supplied from Knudsen cells and the equivalent beam pressures were controlled by a beam flux monitor. During the growth of the Fe3GeTe2 thin film, the equivalent beam pressures of Fe, Ge and Te were kept at PFe = 1.0 × 10−6 Pa, PGe = 2.5 × 10−6 Pa and PTe = 1.0 × 10−4 Pa, respectively. The growth rate of Fe3GeTe2 was approximately 0.4 nm per minute. The (Bi,Sb)2Te3 buffer layer was grown with PBi = 2.5 × 10−6 Pa, PSb = 2.5 × 10−6 Pa and PTe = 1.0 × 10−4 Pa. The (Bi,Sb)2Te3 buffer layer has no conductive state due to the hybridization of the topological surface states between the top and the bottom surfaces35, which helps to form the hexagonal Te-based layers of Fe3GeTe2. The crystal structure and the thickness of the film were evaluated by x-ray diffraction and x-ray reflectivity measurement (Supplementary Fig. 6). The resistivity and Hall resistivity were measured by using Physical Property Measurement System (Quantum Design).
Terahertz time-domain spectroscopy (THz-TDS)
The laser pulses with duration of 100 fs from a mode-locked Ti: sapphire laser were split into two paths to generate and detect terahertz pulses. Terahertz pulses were generated and detected by photoconductive antennas. We obtained transmittance spectra by measuring the sample and the bare substrate as a reference. We used the following thin film limit formula to obtain the complex conductivity σxx(ω);
where t (ω), d, Z0 and ns are the complex transmittance, the thickness of the film, the vacuum impedance (377 Ω), and the refractive index of the InP substrate (ns = 3.47), respectively (see also Supplementary Fig. 7a).
Terahertz Faraday rotation measurements
The rotatory component of the transmitted terahertz electric field Ey(t), which is perpendicular to the incident electric field Ex(t), was measured by the Crossed-Nicole configuration by using wire-grid polarizers (The coordinates are illustrated in the schematic of Fig. 2d). The magneto-optical measurement was performed at 0 T after preparing the single ferromagnetic domain by applying the magnetic field of ±1 T. To eliminate the background signal, the polarization rotation Ey(t) at 0 T was calculated by anti-symmetrizing the signals for positive and negative magnetizations. The Fourier transformation of the terahertz pulses Ex(t) and Ey(t) gives the complex Faraday rotation spectra θF(ω) + iηF(ω) ~ Ey(ω)/Ex(ω).
Terahertz Hall conductivity
By using the optical conductivity spectra σxx(ω) and Faraday rotation spectra θF(ω) + iηF(ω), the Hall conductivity spectra were given by,
Kerr rotation measurements
The polar magneto-optical Kerr spectroscopy was performed with use of the photoelastic modulator36. The detection of synchronous signal of the reflected light with the fundamental and second harmonic of the modulation frequency enables us to measure Kerr rotation and ellipticity, respectively. For the measurement, we performed the field cooling from 260 K in the magnetic field ~70 mT with a permanent magnet. The permanent magnet was removed during the measurement. To deduce the Kerr spectra, we anti-symmetrized the spectra for the positive and negative magnetizations.
Optical conductivity σ xx(ω) and Hall conductivity σ xy(ω)
The optical conductivity spectra were obtained by the following procedure. We first measured the reflectivity spectra of Fe3GeTe2 thin film fabricated on InP substrate from 0.01 to 5 eV (Supplementary Fig. 7b), and then deduced the complex reflection coefficient rtot through the Kramers–Kronig (KK) transformation. Considering the multiple reflections within the thin film, rtot is given by Kim et al.37,
where k = nfilmω/c is the wave number of the light inside the film, d is the thickness of the film, and nfilm and nsub are the complex refractive indices of the film and the substrate, respectively. By substituting this equation into the experimental rtot, we calculated nfilm numerically. Here, we used nsub deduced through the KK transformation from the reflectivity spectra of InP substrate. Finally, the optical conductivity spectra of the Fe3GeTe2 thin film were calculated based on the following equation;
We note that the KK analysis is not strictly applicable to the reflectance for the unpolarized light in time-reversal broken materials due to the emergence of the circular dichroism. In the present material, however, the circular dichroism is small enough, given the small Kerr ellipticity of around a few mrad. Therefore, the measured reflectance for the unpolarized light should give the almost same reflectance for the circularly polarized light, supporting the validity of applying the KK analysis to deduce the diagonal tensor components of conductivity σxx(ω). We further examine the validity of the present KK analysis by deducing the optical conductivity spectra in another way. We measured the transmittance T and reflectance R from 0.1 to 0.5 eV (Supplementary Fig. 8a) and determine the optical conductivity numerically at each energy so as to reproduce simultaneously T and R data. The R including the multiple reflections within the thin film and the T including those within the thin film and substrate are given by37,38;
We numerically solve these equations and find that the obtained results deduced in the two different ways agree well with each other (Supplementary Fig. 8b). We note also that the 2-nm-thick semi-insulating (Bi,Sb)2Te3 layer is negligible for the optical properties of Fe3GeTe2 film (see also Supplementary Note 5 and Supplementary Fig. 9).
When θK and ηK «1, the optical Hall conductivity spectra σxy(ω) are given as37,
Density functional calculation
The electronic structure of Fe3GeTe2 was calculated by using the OpenMX code39, where the exchange-correlation functional within the local spin density approximation40 and norm-conserving pseudopotentials41 were employed. The spin-orbit coupling was included by using total angular momentum dependent pseudopotentials42. The wave functions were expanded by a linear combination of multiple pseudo-atomic orbitals43. A set of pseudo-atomic orbital basis was specified as Fe6.0-s3p3d3f1, Ge7.0-s3p3d2f1, Te7.0-s3p3d3f1, where the number after each element stands for the radial cutoff in the unit of Bohr and the integer after s, p, d and f indicates the radial multiplicity of each angular momentum component. The cutoff-energy for charge density of 300.0 Ry and a k-point mesh of 31 × 31 × 15 were used. The lattice constant of Fe3GeTe2 was set to a = 3.991 and c = 16.336 Å. The magnetic moment is evaluated as 2.2 (μB/Fe) in this calculation.
Wannier representation and optical conductivities
From the Bloch states obtained in the DFT calculation described above, a Wannier basis set was constructed by using the Wannier90 code44. The basis was composed of d-character orbitals localized at each Fe site and p-character ones at each Ge and Te site, which are 96 orbitals/f.u. of Fe3GeTe2 in total if including the spin multiplicity. These sets were extracted from 301 bands in the space spanned by the original Bloch bands at the energy range from −15 to +30 eV.
The optical conductivity and optical Hall conductivity spectra were calculated by using Kubo–Greenwood formula given as,
where e, ħ, Ωc, Nk, η, fn,k are the elementary charge with negative sign, reduced Planck constant, cell volume, number of k-point, smearing parameter, and the Fermi-Dirac distribution function with the band index n and the wave vector k, respectively. The σαβ(ħω) was calculated using the Wannier-interpolated band structure with a 100 × 100 × 100 k-point grid and η = 20 meV. To discuss the optical Hall conductivity spectra arising from the nodal line around Fermi level, we chose six bands connected to the nodal line indicated by red curves in Fig. 4c. We also calculate the optical Hall conductivity spectra when the initial states of the optical transitions are limited to the bands located from −0.8 to −0.5 eV to evaluate the contribution from the flat bands. We note that all the calculated spectra are multiplied by a factor of 1/8 for the qualitative comparison. We discuss this quantitative difference in more detail in Supplementary Note 2.
Data availability
The data that support the plots of this study are available from the corresponding author upon reasonable request.
References
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Nagaosa, N., Morimoto, T. & Tokura, Y. Transport, magnetic and optical properties of Weyl materials. Nat. Rev. Mater. 5, 621–636 (2020).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Sakai, A. et al. Iron-based binary ferromagnets for transverse thermoelectric conversion. Nature 581, 53–57 (2020).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 3681 (2018).
Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 14, 1119–1124 (2018).
Belopolski, I. et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278–1281 (2019).
Kim, K. et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794–799 (2018).
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).
Minami, S. et al. Enhancement of the transverse thermoelectric conductivity originating from stationary points in nodal lines. Phys. Rev. B 102, 205128 (2020).
Wu, L. et al. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 13, 350–355 (2017).
Osterhoudt, G. B. et al. Colossal mid-infrared bulk photovoltaic effect in a type-I Weyl semimetal. Nat. Mater. 18, 471–475 (2019).
Jiang, W. et al. Giant anomalous Hall effect due to double-deenerate quasiflat bands. Phys. Rev. Lett. 126, 106601 (2021).
Iguchi, S. et al. Optical probe for anomalous hall resonance in ferromagnets with spin chirality. Phys. Rev. Lett. 103, 267206 (2009).
Shimano, R. et al. Terahertz Faraday rotation induced by an anomalous Hall effect in the itinerant ferromagnet SrRuO3. Europhys. Lett. 95, 17002 (2011).
Okamura, Y. et al. Giant magneto-optical responses in magnetic Weyl semimetal Co3Sn2S2. Nat. Commun. 11, 4619 (2020).
Deng, Y. et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018).
Chen, B. et al. Magnetic properties of layered itinerant electron ferromagnet Fe3GeTe2. J. Phys. Soc. Jpn. 82, 124711 (2013).
May, A. F., Calder, S., Cantoni, C., Cao, H. & McGuire, M. A. Magnetic structure and phase stability of the van der Waals bonded ferromagnet Fe3-xGeTe2. Phys. Rev. B 93, 014411 (2016).
Fei, Z. et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 17, 778–782 (2018).
Tan, C. et al. Hard magnetic properties in nanoflake van der Waals Fe3GeTe2. Nat. Commun. 9, 1554 (2018).
Liu, S. et al. Wafer-scale two-dimensional ferromagnetic Fe3GeTe2 thin films grown by molecular beam epitaxy. npj 2D Mater. Appl. 1, 30 (2017).
Zhang, Y. et al. Emergence of Kondo lattice behavior in a van der Waals itinerant ferromagnet, Fe3GeTe2. Sci. Adv. 4, eaao6791 (2018).
Xu, J. et al. Large anomalous Nernst effect in a van der Waals ferromagnet Fe3GeTe2. Nano Lett. 19, 8250–8254 (2019).
Roemer, R., Liu, C. & Zou, K. Robust ferromagnetism in wafer-scale monolayer and multilayer Fe3GeTe2. npj 2D Mater. Appl. 4, 33 (2020).
Tran, D. T., Dauphin, A., Grushin, A. G., Zoller, P. & Goldman, N. Probing topology by ‘heating’: quantized circular dichroism in ultracold atoms. Sci. Adv. 3, e1701207 (2017).
Tse, W.-K. & MacDonald, A. H. Giant magneto-optical Kerr effect and universal Faraday effect in thin-film topological insulators. Phys. Rev. Lett. 105, 057401 (2010).
Kang, M. et al. Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 19, 163–169 (2020).
Zhang, Z. et al. Flat bands in twisted bilayer transition metal dichalcogenides. Nat. Phys. 16, 1093–1096 (2020).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Zhang, Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584–588 (2010).
Ohgushi, K., Okimoto, Y., Ogasawara, T., Miyasaka, S. & Tokura, Y. Magnetic, optical, and magnetooptical properties of spinel-type ACr2X4 (A = Mn, Fe, Co, Cu, Zn, Cd; X = O, S, Se). J. Phys. Soc. Jpn. 77, 034713 (2008).
Kim, M.-H. et al. Determination of the infrared complex magnetoconductivity tensor in itinerant ferromagnets from Faraday and Kerr measurements. Phys. Rev. B 75, 214416 (2007).
Nilsson, P.-O. Determination of optical constants from intensity measurements at normal incidence. Appl. Opt. 7, 435–441 (1968).
OpenMX: Open source package for Material eXplorer. http://www.openmx-square.org/.
Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566–569 (1980).
Morrison, I., Bylander, D. M. & Kleinman, L. Nonlocal Hermitian norm-conserving Vanderbilt pseudopotential. Phys. Rev. B 47, 6728 (1993).
Theurich, G. & Hill, N. A. Self-consistent treatment of spin-orbit coupling in solids using relativistic fully separable ab initio pseudopotentials. Phys. Rev. B 64, 073106 (2001).
Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 67, 155108 (2003).
Pizzi, G. et al. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 32, 165902 (2020).
Acknowledgements
We thank R. Kaneko and N. Ogawa for experimental help. This work was partially supported by JSPS KAKENHI (Grant no. 19K14653, 16H06345) and JST CREST (JPMJCR16F1, JPMJCR1874 and JPMJCR18T2).
Author information
Authors and Affiliations
Contributions
Y.Tokura and Y.Takahashi conceived the project. Y.D.K. and Y.O. performed the optical measurement and analyzed the data under supervision of Y.Takahashi. R.F., M.M. and R.Y. fabricated and characterized the thin film under supervision of A.T., K.S.T., M.K. and Y.Tokura. S.M. and R.A. calculated the band structure and optical spectra. Y.D.K., Y.O., Y.Tokura and Y.Takahashi discussed and interpreted the results with inputs from other authors. Y.D.K., Y.O. and Y.Takahashi wrote the manuscript with assistance of other authors. Y.D.K. and Y.O. contributed to this work equally.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41535_2022_482_MOESM1_ESM.pdf
Supplemental information for “Optical anomalous Hall effect enhanced by flat bands in ferromagnetic van der Waals semimetal”
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kato, Y.D., Okamura, Y., Minami, S. et al. Optical anomalous Hall effect enhanced by flat bands in ferromagnetic van der Waals semimetal. npj Quantum Mater. 7, 73 (2022). https://doi.org/10.1038/s41535-022-00482-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00482-2
This article is cited by
-
Critical enhancement of the spin Hall effect by spin fluctuations
npj Quantum Materials (2024)
-
Terahertz linear/non-linear anomalous Hall conductivity of moiré TMD hetero-nanoribbons as topological valleytronics materials
Scientific Reports (2024)
-
Charge dynamics of a noncentrosymmetric magnetic Weyl semimetal
npj Quantum Materials (2022)