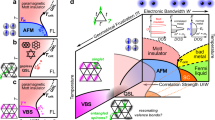
Abstract
The quantum spin liquid candidate NaYbSe2 was recently reported to exhibit a Mott transition under pressure. Superconductivity was observed in the high-pressure metallic phase, raising the question concerning its relation with the low-pressure quantum spin liquid ground state. Here we combine the density functional theory and the dynamical mean-field theory to explore the underlying mechanism of the insulator-to-metal transition and superconductivity and establish an overall picture of its electronic phases under pressure. Our results suggest that NaYbSe2 is a charge-transfer insulator at ambient pressure. Upon increasing pressure, however, the system first enters a semi-metallic state with incoherent Kondo scattering against coexisting localized Yb-4f moments, and then turns into a heavy-fermion metal. In between, there may exist a delocalization quantum critical point responsible for the observed non-Fermi liquid region with linear-in-T resistivity. The insulator-to-metal transition is therefore a two-stage process. Superconductivity emerges in the heavy-fermion phase with well-nested Yb-4f Fermi surfaces, suggesting that spin fluctuations may play a role in the Cooper pairing. NaYbSe2 might therefore be the 3rd Yb-based heavy-fermion superconductor with a very “high” Tc than most heavy-fermion superconductors.
Similar content being viewed by others
Introduction
Quantum spin liquid (QSL) is a highly entangled state with nontrivial topological excitations1,2,3,4. It has attracted intensive interest in modern condensed matter physics and is believed to describe the ground state of the Mott insulator and, upon doping, can induce high-temperature superconductivity as in cuprates5,6,7,8,9. Tremendous efforts have thus been devoted to exploring candidate spin liquid compounds10,11,12,13,14,15,16 and searching for potential sign of superconductivity via chemical substitution17,18. However, doping typically introduces disorder that may obscure the investigation of such delicate intrinsic properties.
Recently, superconductivity has been reported by pressurizing the QSL candidate NaYbSe219,20. In contrast to YbMgGaO4 which has the same structure (space group R-3mH) but with Mg/Ga disorders21,22,23,24,25,26,27,28,29,30, NaYbSe2 contains no intrinsic site disorder and has arguably the simplest crystal structure and chemical formula among all existing QSL candidates31. At ambient pressure, analyses of transport and neutron data found an insulating charge gap of 1.9 eV32 and a crystalline excitation energy of about 15.7 meV33,34,35. No magnetic or structural transition was observed down to 50 mK32,33,34. Neutron scattering measurement has revealed the signature of magnetic excitation continuum and supported a QSL ground state34. The low-energy physics may thus be described by an effective spin-\(\frac{1}{2}\) model on a perfect triangular lattice formed by Yb ions. At 11 GPa, a structural transition was reported19. The high-pressure structure has a lower symmetry (space group P-3m1) with two inequivalent Yb ions of different Yb-Se distances19. Upon further increasing pressure, an insulator-to-metal transition appears at about 58.9 GPa and superconductivity emerges over a wide pressure range above 103.4 GPa with a maximum Tc of about 8 K19. The insulator-to-metal transition was claimed to be of Mott type, raising the question concerning the relationship between the low-pressure QSL and the high-pressure superconductivity.
To clarify the nature of the “Mott” transition and the superconducting pairing mechanism, we investigate here the electronic structure of NaYbSe2 and its pressure evolution using the density functional theory (DFT) plus the dynamical mean-field theory (DMFT) calculations36,37,38,39. We find that NaYbSe2 is a charge-transfer insulator at ambient pressure, with the charge gap formed between Se-3p bands and Yb-4f upper-Hubbard bands. The charge gap is closed near about 60 GPa, giving rise to an intermediate semi-metallic phase with small electron and hole pockets from Yb-5d and Se-3p bands, respectively. The Yb-4f electrons remain localized at this pressure and the system is a typical low carrier density Kondo system, which explains the logarithmic temperature dependence of the resistivity observed in transport measurements. Above 73 GPa, the Yb-4f moments are fully screened on one (Yb1) of the two inequivalent Yb-ions, giving rise to flat heavy electron bands near the Fermi energy with sharp quasiparticle peaks in the density of states. The system turns into a heavy-fermion metal. But the 4f electrons on the other Yb-ions (Yb2) remain localized and only weakly hybridized with conduction electrons. Superconductivity emerges in the heavy-fermion phase when the Yb1-4f Fermi surfaces develop a well-nested quasi-two-dimensional structure. The nesting wave vector coincides with the antiferromagnetic wave vector of the localized spins, indicating possible involvement of heavy electrons and antiferromagnetic spin fluctuations. NaYbSe2 might therefore be the 3rd Yb-based heavy-fermion superconductor with a rather “high” transition temperature (Tc ~ 8 K) among all heavy-fermion superconductors.
Results and discussion
Optimization of crystal structures
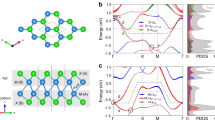
The crystal structures of NaYbSe2 at low and high pressures are compared in Fig. 1a, both composed of edge-shared YbSe6 and NaSe6 octahedra. The Yb ions form a layer structure of flat triangular lattices with the shortest Yb-Yb distance in the ab plane for both structures19. The lattice parameters have been measured below 32 GPa in experiment19,20. For numerical calculations, we have used DFT+U to optimize the lattice parameters for both structures40,41,42 and the results are compared with existing experimental data in Fig. 1b. Their good agreement over the whole low-pressure range validates the starting point of our numerical calculations.
Electronic structures at low pressures
The electronic structures of NaYbSe2 were obtained using DFT+DMFT with the hybridization expansion continuous-time quantum Monte Carlo (CT-HYB) as the impurity solver43,44, taking into account both the spin–orbit coupling and electronic correlations. A Coulomb interaction U = 6 eV was chosen to reproduce the correct charge gap of about 1.9 eV at ambient pressure estimated from absorption spectra measurements32. Figure 1c plots the calculated density of states and spectral function at T = 10 K and ambient pressure. The Yb-4f Hubbard bands are located at about −3.0 and 2.0 eV, respectively, with a clear charge gap between the Se-3p bands and the Yb-4f upper-Hubbard bands. Hence NaYbSe2 should be identified as a charge-transfer insulator at ambient pressure. Without DMFT, DFT+U calculations alone yield a much larger Yb occupation number and predict incorrectly a metallic ground state, in disagreement with experiment. The band structures at 20 GPa are compared in Fig. 1d. We have now two inequivalent Yb-ions. Their 4f Hubbard bands become blurred, and the Yb-5d bands move down closer to the Fermi energy to form a smaller normal band insulating gap with the slightly upshifted Se-3p bands.
The intermediate semi-metallic state
Upon further increasing pressure, our calculations reveal a sequence of electronic phases, in good correspondence with the experimental observation. This is summarized in the upmost plot of Fig. 2. The first transition occurs near about 60 GPa, where the charge gap is closed and the spectral function reveals a semi-metallic state with a small electron pocket at the M point from Yb-5d bands and a hole pocket at Γ from Se-3p bands, as shown in Fig. 2a. However, the Yb-4f electrons are still localized at this pressure. In Fig. 2d, we see a tiny pseudogap structure near the Fermi energy in the 4f partial density of states, indicating a weak hybridization with conduction bands. Thus NaYbSe2 should be better identified as a low carrier density Kondo system at this pressure. Consequently, there are not enough conduction electrons to screen the Yb-4f local moments so that the resistivity should be dominated by incoherent Kondo scattering and exhibit typical logarithmic temperature dependence45,46. This has indeed been observed in experiment between 58.9 and 74.8 GPa, but was initially attributed to weak localization19. We argue that similar properties, including the logarithmic-in-T resistivity and a pseudogap in the quasiparticle density of states, have previously been discussed in other low carrier density Kondo systems45,46,47,48. Since no magnetic long-range order has been observed in experiment under pressure19, the weak hybridization in this regime suggests that the 4f spins on both Yb ions should still be in their respective spin liquid states as reported by neutron scattering at ambient pressure34.
The upper figure illustrates the predicted phases: the charge-transfer or band insulator, the Kondo semimetal (Kondo), the heavy-fermion metal (HF), and the superconductivity (SC). The pressures denote a rough boundary of these phases from experiment19. a–c The DFT+DMFT spectral functions at 10 K for 60, 75, and 100 GPa, respectively. d–f The corresponding density of states on two inequivalent Yb ions, showing the development of a sharp quasiparticle peak of Yb1-4f electrons. The inset in d is an enlarged plot over a smaller energy window to show the pseudogap structure near the Fermi energy at 60 GPa. The inset in e plots the full width at half maximum (FWHM) of the Yb1 quasiparticle peak as a function of pressure, where the solid line is a linear extrapolation giving a transition at about 73 GPa.
Heavy-fermion metal at high pressure
The second transition occurs close to 75 GPa beyond which flat heavy electron bands are seen to develop near the Fermi energy in Fig. 2b, c. Correspondingly, a sharp quasiparticle peak appears at the Fermi energy in the Yb1-4f density of states shown in Fig. 2e, f due to the many-body Kondo effect. The system now turns into a good heavy-fermion metal. To determine the exact transition point, we plot in the inset of Fig. 2e the full width at half maximum (FWHM) of the Yb1-4f quasiparticle peak. Its variation with pressure reflects tentatively the strength of the Kondo hybridization49. A linear extrapolation to zero suggests that the transition occurs at about 73 GPa, which separates the low carrier density Kondo phase and the heavy-fermion metal. Thus, it marks a delocalization transition of the Yb1-4f electrons. Interestingly, experiment did observe a non-Fermi liquid state with linear-in-T resistivity near 74.8 GPa and beyond that a gradual crossover to the Fermi liquid at 126 GPa19. This agrees with our theory and strongly suggests the possible existence of a delocalization quantum critical point at zero temperature. The nature of the non-Fermi liquid phase is still under debate50,51. However, the broad crossover region is quite unusual and might be associated with the special layer structure of NaYbSe2 to be discussed later. Nevertheless, the insulator-to-metal transition is not a simple Mott transition, but a two-stage process first from a normal band insulator to a semimetal with incoherent Kondo scattering and then to a heavy-fermion metal. Similar transition and non-Fermi liquid property have also been reported in the low carrier density Kondo system CeNi2−δ(As1−xPx)246.
It may be interesting to mention that pressure seems to favor the heavy-fermion phase in NaYbSe2, while in many other Yb-based heavy-fermion compounds, the Kondo effect is typically weakened under pressure and gives in to long-range magnetic orders because of the upshift of the Yb-4f hole (upper-Hubbard) bands further away from the Fermi energy, suppressing possible charge fluctuations and making Yb-4f electrons more localized. In NaYbSe2, however, our results show that the localized Yb-4f levels are already away from the Fermi energy with a stable Yb3+ configuration and the major effect of pressure is to increase the carrier density and enhance the hybridization as will be discussed below. Such anomalous increase of the Kondo effect with pressure has previously been observed in Yb2Ni2Al and YbCu2Si252,53 but attributed to the electron-lattice coupling54. Here NaYbSe2 provides an interesting alternative for further investigation.
Alternating heavy-fermion and QSL layers
To have a better understanding of the peculiarity of NaYbSe2, we compare in Fig. 3a, b the imaginary part of the Yb-4f hybridization function at four typical pressures. Quite remarkably, this reveals an unexpected but substantial difference between the two inequivalent Yb ions. While no hybridization is observed near the Fermi energy on both ions at low pressure (20 GPa), it begins to develop on Yb1 at 60 GPa and becomes large above 75 GPa, but on Yb2 the hybridization remains weak over the whole pressure range and shows no significant enhancement. These suggest that only Yb1 ions are responsible for the flat bands and heavy-fermion properties at high pressure, while Yb2-4f electrons remain localized and weakly interacting with conduction electrons. These observations are further confirmed in the local spin susceptibility, \({\chi }_{zz}(\omega )={ \langle {S}_{z}(\tau ){S}_{z}(0) \rangle }_{\omega }\), calculated using the CT-HYB impurity solver. Here Sz is the local spin operator of the Yb-4f electrons and τ is the imaginary time. As shown in Fig. 3c, the static susceptibility of Yb1 deviates from the Curie-Weiss law at low temperature above 75 GPa due to the Kondo hybridization, but that of Yb2 always follows the Curie-Weiss law and keeps the local moment behavior. This explains the absence of quasiparticle resonance in the Yb2-4f density of states plotted earlier in Fig. 2f. To understand these huge differences between Yb1 and Yb2 ions, we compare in Fig. 3d their local environment, namely their respective Yb-Se bond distances. With increasing pressure from 20 to 100 GPa, the Yb1-Se distance is seen to decrease from 2.67 to 2.37 Å, while the Yb2-Se distance decreases from 3.0 to 2.66 Å. Hence the Yb2-Se distance at 100 GPa is roughly equal to the Yb1-Se distance at 20 GPa, explaining why the Yb2-4f electrons are still localized at such high pressure.
a, b Pressure evolution of the minus imaginary part of the hybridization function in real frequency on Yb1 and Yb2 ions from 20 to 100 GPa, obtained by DFT+DMFT calculations at 10 K. c Comparison of static local spin susceptibility of Yb1 and Yb2 4f-electrons at 60, 75, and 100 GPa. d Comparison of the Yb-Se distances as a function of pressure from 20 to 100 GPa.
Note that it is not our purpose here to predict either magnetic ordering or spin liquidity based purely on numerical calculations. Our strategy is to connect the calculated electronic structures with experimental observations of these physical properties. Since in experiment there is no magnetic ordering observed under pressure19, the Yb2-4f spins in this pressure region should remain in a spin liquid state34. We thus conclude that the high-pressure structure of NaYbSe2 contains alternating Yb1 heavy-fermion layers and Yb2 QSL layers, a very peculiar structure for studying the interplay between the two exotic quantum many-body states. It is wondering if this might be responsible for the broad crossover to the Fermi liquid behavior observed in the resistivity19.
Superconductivity
Experimentally, superconductivity in NaYbSe2 emerges above 103 GPa in the heavy Fermi liquid phase19. To explore possible connection between the pairing and electronic band structures, we compare in Fig. 4a–c the Fermi surface topology at 60, 75, and 100 GPa, respectively. At 60 GPa, the Fermi surfaces only consist of small electron and hole pockets centered at M and Γ points. The small Fermi volume reflects a low carrier density of the semi-metallic phase for incoherent Kondo scattering. At 75 GPa, the Fermi surfaces become larger with three cylinders around Γ and a small electron pocket around the M point. At 100 GPa, the cylindrical Fermi surfaces continue to grow but the electron pocket at M is gapped out and diminishes due to strong hybridization. We find superconductivity emerges as the Fermi surfaces become well nested and quasi-two-dimensional. This is seen in Fig. 4d–f, where we plot the real part of the Lindhard susceptibility derived from DFT+DMFT Fermi surfaces. Only beyond 100 GPa, we find a well-defined nesting wave vector. This suggests an intimate connection between superconductivity and the Fermi surface topology and hints that the Fermi surface nesting and its resulting spin density wave fluctuations may play a major role in the Cooper pairing. Moreover, the nesting pattern is in close resemblance to that of the spin excitation spectra of the Heisenberg model on the same lattice as revealed by neutron scattering experiment at ambient pressure34. Considering that the Yb2 layers remain in a QSL state, it may be natural to wonder if their associated magnetic fluctuations may also be involved in the electron pairing. At this stage, phonons also cannot be excluded. But in any case, since NaYbSe2 is in a heavy-fermion state at this pressure, the itinerant heavy Yb1-4f quasiparticles must participate in the superconductivity, making it a candidate heavy-fermion superconductor. If this is the case, it would be the 3rd Yb-based heavy-fermion superconductor, in addition to YbRh2Si2 of Tc ~ 2 mK55 and β-YbAlB4 of Tc ~ 80 mK56. The transition temperature of about 8 K in NaYbSe2 is strikingly high among all heavy-fermion superconductors except Pu-115, probably suggesting a potential cooperation of the Fermi surface nesting, spin fluctuations, and phonons. For such a Fermi surface topology with the antiferromagnetic nesting wave vector, group-theoretical analyses favor a spin-singlet pairing state with gap symmetries listed in Table 1. We have either a nodeless s-wave pairing (A1g) or a two-component d-wave pairing (Eg), with possible accidental line nodes for appropriate combination of the basis functions, or a less probable g-wave gap (A2g) with loop nodes in the kz = 0 plane. More elaborate experiments are needed for better clarification but would be extremely difficult under such high pressures. It will be important if superconductivity can be found at lower pressures in other members of the same family through chemical substitution.
Summary
Our calculations reveal a sequence of electronic phases in pressurized QSL candidate NaYbSe2. We find that it is a charge-transfer insulator at ambient pressure and turns into a low carrier density Kondo system with semi-metallic band structures close to 60 GPa and a good heavy-fermion metal above 73 GPa. In between, we predict a delocalization quantum critical point of the Yb1-4f electrons that may explain the observed non-Fermi liquid with linear-in-T resistivity, while the Yb2-4f electrons remain localized over the whole pressure range. The lattice therefore has a special structure constructed with alternating Yb1 heavy-fermion layers and Yb2 QSL layers. Superconductivity emerges in the heavy-fermion metal with well nested quasi-two-dimensional Fermi surfaces, making NaYbSe2 possibly the 3rd Yb-based heavy-fermion superconductor with a record-high Tc. This suggests the possible involvement of both spin fluctuations and phonons as the pairing glues. Our work will be a useful guide for future experimental study of NaYbSe2 and its other family members.
Methods
DFT calculations
DFT calculations were performed using the full-potential augmented plane-wave plus local orbital method as implemented in the WIEN2k package40 and the Perdew–Burke–Ernzerhof exchange-correlation potential42. The lattice parameters were optimized using DFT+U with an effective Coulomb interaction of 6 eV41. The plane-wave cutoff \({K}_{\max }\) was chosen to make \({R}_{{{{\rm{MT}}}}}\times {K}_{\max }=8.0\). All calculations were performed on a grid of 1000 k-points in the Brillouin zone. The spin–orbit coupling was included explicitly.
DFT+DMFT calculations
DFT+DMFT calculations were employed to treat the electronic correlations of Yb-4f orbitals. The hybridization expansion continuous-time quantum Monte Carlo (CT-HYB) was used as the impurity solver43,44. Yb-4f local orbitals were constructed using projectors with an energy window from −10 to 10 eV relative to the Fermi energy. The Coulomb interaction was chosen to be U = 6 eV and JH = 0.7 eV. A nominal double-counting scheme with nf = 13.0 was used. The self-energy in real frequency was obtained by analytic continuation based on the maximum entropy38,57.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
We have used the WIEN2k40 and DFT+eDMFT codes38 to generate the data. WIEN2k is a commercially available software package and DFT+eDMFT can be obtained from http://hauleweb.rutgers.edu.
References
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Broholm, C. et al. Quantum spin liquids. Science 367, eaay0668 (2020).
Anderson, P. W. Resonating valence bounds: a new kind of insulator? Mat. Res. Bull. 8, 153–160 (1973).
Wen, X. G. Mean-field theory of spin-liquid states with finite energy gap and topological orders. Phys. Rev. B 44, 2664–2672 (1991).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Wen, J., Yu, S.-L., Li, S., Yu, W. & Li, J.-X. Experimental identification of quantum spin liquids. npj Quantum Mater. 4, 12 (2019).
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Kelly, Z. A., Gallagher, M. J. & McQueen, T. M. Electron doping a Kagome spin liquid. Phys. Rev. X 6, 041007 (2016).
Kurosaki, Y., Shimizu, Y., Miyagawa, K., Kanoda, K. & Saito, G. Mott Transition from a spin liquid to a Fermi liquid in the spin-frustrated organic conductor κ − (ET)2Cu2(CN)3. Phys. Rev. Lett. 95, 177001 (2005).
Shimizu, Y. et al. Pressure-tuned exchange coupling of a quantum spin liquid in the molecular triangular lattice κ − (ET)2Ag2(CN)3. Phys. Rev. Lett. 117, 107203 (2016).
Furukawa, T., Kobashi, K., Kurosaki, Y., Miyagawa, K. & Kanoda, K. Quasi-continuous transition from a Fermi liquid to a spin liquid in κ − (ET)2Cu2(CN)3. Nat. Commun. 9, 307 (2018).
Powell, B. J. & McKenzie, R. H. Quantum frustration in organic Mott insulators: from spin liquids to unconventional superconductors. Rep. Prog. Phys. 74, 056501 (2011).
Clancy, J. P. et al. Pressure-driven collapse of the relativistic electronic ground state in a honeycomb iridate. npj Quantum Mater. 3, 35 (2018).
Podolsky, D., Paramekanti, A., Kim, Y. B. & Senthil, T. Mott Transition between a spin-liquid insulator and a metal in three dimensions. Phys. Rev. Lett. 102, 186401 (2009).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Lee, P. A. From high temperature superconductivity to quantum spin liquid: progress in strong correlation physics. Rep. Prog. Phys. 71, 012501 (2008).
Jia, Y.-T. et al. Mott transition and superconductivity in quantum spin liquid candidate NaYbSe2. Chin. Phys. Lett. 37, 097404 (2020).
Zhang, Z. et al. Pressure induced metallization and possible unconventional superconductivity in spin liquid NaYbSe2. Preprint at https://arXiv.org/abs/2003.11479 (2020).
Li, Y. et al. Gapless quantum spin liquid ground state in the two-dimensional spin-1/2 triangular antiferromagnet YbMgGaO4. Sci. Rep. 5, 16419 (2015).
Zhu, Z., Maksimov, P. A., White, S. R. & Chernyshev, A. L. Disorder-induced mimicry of a spin liquid in YbMgGaO4. Phys. Rev. Lett. 119, 157201 (2017).
Li, Y. et al. Rare-earth triangular lattice spin liquid: a single-crystal study of YbMgGaO4. Phys. Rev. Lett. 115, 167203 (2015).
Li, Y. et al. Muon spin relaxation evidence for the U(1) quantum spin-liquid ground state in the triangular antiferromagnet YbMgGaO4. Phys. Rev. Lett. 117, 097201 (2016).
Shen, Y. et al. Evidence for a spinon Fermi surface in a triangular-lattice quantum-spin-liquid candidate. Nature 540, 559–562 (2016).
Li, Y. et al. Crystalline electric-field randomness in the triangular lattice spin-liquid YbMgGaO4. Phys. Rev. Lett. 118, 107202 (2017).
Zhu, Z., Maksimov, P. A., White, S. R. & Chernyshev, A. L. Topography of spin liquids on a triangular lattice. Phys. Rev. Lett. 120, 207203 (2018).
Li, Y.-D., Wang, X. & Chen, G. Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets. Phys. Rev. B 94, 035107 (2016).
Li, Y.-D., Lu, Y.-M. & Chen, G. Spinon Fermi surface U(1) spin liquid in the spin-orbit-coupled triangular-lattice Mott insulator YbMgGaO4. Phys. Rev. B 96, 054445 (2017).
Kimchi, I., Nahum, A. & Senthil, T. Valence bonds in random quantum magnets: theory and application to YbMgGaO4. Phys. Rev. X 8, 031028 (2018).
Gray, A. K., Martin, B. R. & Dorhout, P. K. Crystal structure of sodium ytterbium (III) selenide, NaYbSe2. Z. Kristallogr. NSC 218, 19 (2003).
Liu, W. et al. Rare-earth chalcogenides: a large family of triangular lattice spin liquid candidates. Chin. Phys. Lett. 35, 17501 (2018).
Ranjith, K. M. et al. Anisptropic field-induced ordering in the triangular-lattice quantum spin liquid NaYbSe2. Phys. Rev. B 100, 224417 (2019).
Dai, P.-L. et al. Spinon Fermi surface spin liquid in a triangular lattice antiferromagnet NaYbSe2. Phys. Rev. X 11, 021044 (2021).
Zhang, Z. et al. Crystalline electric field excitations in the quantum spin liquid candidate NaYbSe2. Phys. Rev. B 103, 035144 (2021).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Held, K., Andersen, O. K., Feldbacher, M., Yamasaki, A. & Yang, Y.-F. Bandstructure meets many-body theory: the LDA+DMFT method. J. Phys.: Condens. Matter 20, 064202 (2008).
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2K: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties (Vienna, Techn. Universität Wien, 2014).
Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method. J. Phys. Condens. Matter 9, 767–808 (1997).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Werner, P., Comanac, A., de’ Medici, L., Troyer, M. & Millis, A. J. Continuous-time solver for quantum impurity models. Phys. Rev. Lett. 97, 076405 (2006).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Luo, Y. et al. Pressure-tuned quantum criticality in the antiferromagnetic Kondo semimetal CeNi2−δAs2. Proc. Natl. Acad. Sci. USA 112, 13520–13524 (2015).
Chen, J. et al. Heavy fermion quantum criticality at dilute carrier limit in CeNi2−δ(As1−x Px)2. Sci. Rep. 9, 12307 (2019).
Nakamoto, G. et al. Effect of impurity phase on the anisotropic transport properties of CeNiSn. Physica B 206–207, 840–843 (1995).
Takabatake, T. et al. Ce- and Yb-based Kondo semiconductors. J. Magn. Magn. Mater. 177–181, 277–282 (1998).
Krawiec, M. Residual Kondo effect in quantum dot coupled to half-metallic ferromagets. J. Phys.: Condens. Matter 18, 6923–6936 (2006).
Zhao, H. et al. Quantum-critical phase from frustrated magnetism in a strongly correlated metal. Nat. Phys. 15, 1261–1266 (2019).
Wang, J. & Yang, Y.-F. Nonlocal Kondo effect and quantum critical phase in heavy-fermion metals. Phys. Rev. B 104, 165120 (2021).
Winkelmann, H. et al. Pressure-induced local moment magnetism in the nonmagnetic heavy fermion compound Yb2Ni2Al. Phys. Rev. Lett. 81, 4947–4950 (1998).
Winkelmann, H. et al. Direct observation of a magnetically ordered state in YbCu2 Si2 under high pressure. Phys. Rev. B 60, 3324–3330 (1999).
Goltsev, A. V. & Abd-Elmeguid, M. M. Origin of the pressure dependence of the Kondo temperature in Ce- and Yb-based heavy-fermion compunds. J. Phys.: Condens. Matter 17, S813–S820 (2005).
Schuberth, E. et al. Emergence of superconductivity in the canonical heavy-electron metal YbRh2Si2. Science 351, 485–488 (2016).
Nakatsuji, S. et al. Superconductivity and quantum criticality in the heavy-fermion system β-YbAlB4. Nat. Phys. 4, 603–607 (2008).
Jarrell, M. & Gubernatis, J. E. Bayesian inference and the analytic continuation of imaginary-time quantum Monte Carlo data. Phys. Rep. 269, 133–195 (1996).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC Grant Nos. 11974397, 11774401, 12174429), the National Key R&D Program of MOST of China (Grant No. 2017YFA0303103), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB33010100), and the Youth Innovation Promotion Association of CAS. We thank the Tianhe platforms at the National Supercomputer Center in Tianjin for technical support.
Author information
Authors and Affiliations
Contributions
Y.Y. conceived and supervised the project. Y.X. did the calculations. Y.S. contributed to the superconducting analysis. Y.Y., Y.X., and Y.S. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, Y., Sheng, Y. & Yang, Yf. Mechanism of the insulator-to-metal transition and superconductivity in the spin liquid candidate NaYbSe2 under pressure. npj Quantum Mater. 7, 21 (2022). https://doi.org/10.1038/s41535-022-00429-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00429-7