Introduction

Owing to fertile ground of crystalline symmetries, topological gapless phases, characterized by nontrivial band degeneracies, have been undergoing rapid development in condensed matter physics1,2,3. A representative example is the diversification of prototypical Weyl phases. Beyond conventional Weyl fermions with monopole charge ± 14,5,6,7,8,9, unconventional Weyl fermions, which possess a higher monopole charge due to crystalline symmetry, were discovered10,11,12,13,14,15,16,17,18,19. For instance, threefold Weyl fermions with charge ± 2 can be stabilized by a nonsymmorphic symmetry10,11,12,13, and double(triple)-Weyl fermions with a quadratic(cubic) twofold degeneracy can be protected by a rotation symmetry14,15,16,17,18,19.

On the other hand, crystalline symmetries have largely enriched topological gapped phases20,21,22,23,24,25,26,27,28,29,30,31. Among these phases, higher-order topological (HOT) insulators, which feature anomalous boundary states, have drawn particular attention recently32,33,34,35,36,37,38,39,40,41,42,43,44,45. In contrast to conventional bulk-boundary correspondence, i.e., a d-dimensional bulk topology corresponds to (d − 1)-dimensional boundary states, the boundary states of HOT insulators are further restricted by crystalline symmetries and exhibit boundary states in a lower dimension, e.g., corner or hinge states. Recently, it has been found that HOT semimetals (e.g., Dirac, Weyl, and nodal-line) can be realized by nontrivially stacking higher-order insulators46,47,48,49,50,51,52,53,54,55,56,57,58. Specifically, higher-order Weyl semimetals were discovered by stacking two-dimensional (2D) HOT insulators, with broken time-reversal and/or inversion symmetry, in a third dimension50,51,52,53,54,55. Note that in this process, for electronic systems, the Kramers degeneracy of the original HOT insulators, if any, has to be broken before stacking50. In this regard, the higher-order Weyl semimetal phase depends on the 2D sub higher-order phases. The phase transition between these phases results in the higher-order Weyl points, which are typically of conventional type with charge ± 1.

Though topological gapless phases characterized by nontrivial band degeneracies, and topological gapped phases featuring anomalous boundary states, can be stabilized by the same crystalline symmetry, so far, their interplay remains to be explored.

In this work, we develop a theory to generate topological phases of matter, by intertwining existing ones protected by a crystalline symmetry. We discover intertwined Weyl phases, which feature the exotic interplay of unconventional Weyl fermions and higher-order topology. In the bulk, the two phases are independently stabilized by the crystalline symmetry: the Weyl fermions have a monopole charge larger than 1 by the symmetry, and a HOT phase was further superposed by the symmetry. The intertwining results in a specific distribution of the two phases in the bulk, i.e., the higher-order topology exists in the region outside pairs of unconventional Weyl points with opposite charges. Due to their independence, the two phases are separately tunable. The combination of different unconventional Weyl semimetallic and HOT phases results in distinct intertwined Weyl phases. Note that this mechanism is different from the higher-order Weyl semimetal which is determined by the higher-order topology as discussed above.

The intertwined Weyl phases are characterized by the drastic change of Fermi-arc topology on 2D surfaces upon rotating surface termination. This phenomenon comes from the intertwining between the two constituent phases. Even though HOT phases feature boundary states on 1D hinges, they can intertwine with the unconventional Weyl phase on 2D surfaces of the system: Fermi arcs form due to the underlying unconventional Weyl phases, while the topology of these Fermi arcs is drastically changed by the HOT phase. Thus, we identify a prominent topological feature of the intertwined phase: the change of Fermi-arc topology against surface orientation in a periodic pattern. The period is determined by rotation symmetry, e.g., a 2n-fold rotation symmetry leads to a period of π/n. Specifically, we discuss intertwined double-Weyl phases, where double-Weyl fermions and higher-order topology are intertwined due to a fourfold rotation symmetry. The topological phase is characterized by the periodic change of Fermi-arc topology with period π/2. The periodic behavior can be perfectly explained by an effective boundary Hamiltonian, in accordance with our theory. Finally, we show that intertwined double-Weyl phases are realizable in cold-atom experiments, which can serve as a promising platform to implement our theory in experiment.

Results

Intertwining topological phases by crystalline symmetry

We begin by showing how to intertwine topological phases by crystalline symmetry. The essential physics can be captured by the following simple but generic Hamiltonian in 3D momentum space,

$$\begin{array}{ll}H({{{\bf{k}}}})={H}_{{{\mbox{Weyl}}}}+m{{{\Gamma }}}_{{{\mbox{h}}}}\\ \qquad\,\,\,={k}_{+}^{n}{\tau }_{3}{\sigma }_{-}+{k}_{-}^{n}{\tau }_{3}{\sigma }_{+}+{k}_{z}{\tau }_{3}{\sigma }_{3}+m{{{\Gamma }}}_{{{\mbox{h}}}},\end{array}$$
(1)

where k± = kx ± iky, σ± = (σ1 ± iσ2)/2, and σi and τi (i = 1, 2, 3) are Pauli matrices for (pseudo)spin and orbital degrees of freedom, respectively. HWeyl, responsible for generating unconventional Weyl points, is superposed with mΓh, a term for introducing higher-order topology. m is a real model parameter, and Γh a 4 × 4 matrix. After being projected to the boundary, mΓh acts as a mass term that is constrained by the symmetry, as we will discuss in Eqs. (3) and (4). Each of the two parts is invariant under the 2n-fold rotation symmetry C2n about the z axis, with 2n ≤ 6 by lattice restriction (n ∈ {2, 3}).

As shown in Fig. 1, the intertwining can be induced by a crystalline symmetry that superposes the two phases at the same time:

  1. 1.

    The bulk Weyl points with higher monopole charge are stabilized by rotation symmetry. Unconventional Weyl points with charge ±n (n > 1) can be generated by breaking time-reversal and/or inversion symmetry in HWeyl. After the substitution of \(({k}_{x},{k}_{y})=(k\cos \theta ,k\sin \theta )\) (Fig. 2a), HWeyl can be rewritten as HWeyl(θ) = kne+inθτ3σ− + kne−inθτ3σ+ + kzτ3σ3. As can be seen, these unconventional Weyl points are protected by rotation symmetry14

    $${\hat{C}}_{2n}{H}_{{{\mbox{Weyl}}}}(\theta ){\hat{C}}_{2n}^{-1}={H}_{{{\mbox{Weyl}}}}({R}_{2n}\theta ).$$
    (2)

    Here, \({\hat{C}}_{2n}={\tau }_{3}{\sigma }_{3}\), and R2nθ = θ + π/n acts in momentum space.

  2. 2.

    The higher-order topology is further enforced by rotation symmetry. The topological protection by symmetry can be explicitly demonstrated at the boundary. After projecting the Hamiltonian to the boundary subspace, we can get an effective Hamiltonian on the surface in the form of (See Supplementary Note 2 for derivation details.)

    $${h}_{{{\mathrm{surface}}}}=\mathop{\sum }\limits_{i = 0}^{n}{a}_{i}{k}_{\parallel }^{i}{\sigma }_{3}+m(\theta ){\gamma }_{{{\mathrm{h}}}},$$
    (3)

    where ai is a real coefficient, which may depend on kz, θ is the surface orientation, and k∥ the momentum parallel to the surface (Fig. 2a). The higher-order term m(θ)γh, originated from mΓh, is still rotation-symmetric, \({\hat{c}}_{2n}m({{{{\theta }}}}){\gamma }_{{{\mbox{h}}}}{\hat{c}}_{2n}^{-1}=m({R}_{2n}{{{{\theta }}}}){\gamma }_{{{\mbox{h}}}}\), with the projected rotation operator \({\hat{c}}_{2n}={\sigma }_{3}\). Note that m(θ), which stems from the constant m term in Eq. (1), becomes θ-dependent after the projection by the orientation-dependent boundary wavefunctions. γh anticommutes with σ3, e.g., σ1 or σ2, so that it acts as a mass term in Eq. (3). Thus, we obtain

    $$m({{{{\theta }}}})=-m({R}_{2n}{{{{\theta }}}})=-m(\theta +\pi /n).$$
    (4)

    This relation means m(θ) must have a zero value between θ and θ + π/n, which leads to a gapless point in the surface spectrum. The 1D Hamiltonian (3) for a fixed kz is characterized by a \({\mathbb{Z}}\) topological invariant. Note that the same mechanism leads to HOT insulators protected by crystalline symmetry, where gapless points correspond to corner or hinge modes43,44. Here, as a manifestation of higher-order topology, the gapless points result in 1D hinge states, as shown by the green solid lines in Fig. 1.

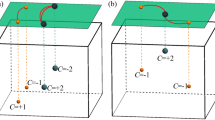
Fig. 1: Intertwining topological phases by crystalline symmetry.
figure 1

Red and blue dots represent Weyl points, and green sold lines denote hinge states from higher-order topology. a The fourfold rotation symmetry (C4) stabilizes double-Weyl points and higher-order topology at the same time. The interplay between the two phases results in an intertwined double-Weyl phase. b The sixfold rotation symmetry (C6) stabilizes triple-Weyl points and higher-order topology at the same time, resulting in an intertwined triple-Weyl phase.

Full size image

The two topological phases in superposition no longer act individually, but intertwine with each other, as we discuss next. Thus, we refer to the resultant phase as “intertwined Weyl phase”, which is different from each individual phase.

We emphasize that in the intertwined Weyl phase, the unconventional Weyl points and the higher-order topology are independently stabilized by the symmetry. This is different from the higher-order Weyl semimetals, where the higher-order Weyl points depend on the HOT phases and are typically conventional ones of topological charge-151,52,53,54,55. Due to the independent nature of the two phases, they can be tuned separately to generate various intertwined Weyl phases. Specifically, different unconventional Weyl fermion phases can be incorporated to build with HOT phase under the same or different crystalline symmetries, resulting in distinct kinds of intertwined Weyl phases, as we will discuss later.

Intertwining and the change of Fermi-arc topology in a periodic pattern

In the bulk, the intertwining results in a specific distribution of the two phases. This is because the higher-order topology cannot survive in regions with non-trivial Chern number. To have vanishing Chern number, it is required that the unconventional Weyl points with opposite charges appear in pairs. In this way, there can exist regions with trivial Chern numbers to host higher-order topology. As shown in Fig. 2 by green arrows, the HOT phase exists outside pairs of unconventional Weyl points with opposite charges.

Fig. 2: The intertwining results in the change of Fermi-arc topology in a periodic pattern.
figure 2

a The relation between different coordinate systems. θ indicates the orientation of the surface (black plane), on which the local density of states is computed numerically. b–d Fermi arcs of intertwined double-Weyl phase in a full period of θ ∈ [0, π/2]. Each projected double-Weyl point emits two Fermi arcs on the surface. The topology of Fermi arcs changes when rotating from the (100) surface (θ = 0) to the (110) surface (θ = π/4), and it returns to the initial topology after rotating further to the (010) surface (θ = π/2), completing one period. e–g Fermi arcs of intertwined triple-Weyl phase in a full period of θ ∈ [0, π/3]. Each projected triple-Weyl point emits three Fermi arcs on the surface. The topology of Fermi arcs changes when rotating from the (1000) surface (θ = 0) to the \((10\bar{1}0)\) surface (θ = π/6), and it returns to the initial topology after rotating further to the \((00\bar{1}0)\) surface (θ = π/3), completing one period.

Full size image

Inside pairs of unconventional Weyl points, e.g., the lower and upper two sets of Weyl points in Fig. 2b, there is no m(θ), the surface Hamiltonian (3) describes Fermi arcs like those in unconventional Weyl semimetals. On 2D surfaces, the existence of these Fermi arcs is isotropic, i.e., they do not depend on surface orientation θ. However, in HOT regions, the HOT term m(θ) exists. The existence of Fermi arcs in this region depends on m(θ) and becomes anisotropic. We find that due to the intertwining of the two parts of Fermi arcs, the Fermi-arc topology on 2D surfaces is drastically changed. We use m(θ) in Eq. (4) to explain the phenomenon in detail below.

First, the gapless point enforced by the HOT phase in Eq. (4) crucially affects the Fermi-arc topology. We use the spectrum of the surface Hamiltonian (3), \({E}_{{{\mbox{surface}}}}=\pm \sqrt{{(\mathop{\sum }\nolimits_{i = 0}^{n}{a}_{i}{k}_{\parallel }^{i})}^{2}+{m}^{2}({{{{\theta }}}})}\), for illustration. If there is no gapless point [m(θ) ≠ 0] in the HOT phase region for a specific angle θ, no Fermi arc can go through this HOT phase region because Esurface is gapped, e.g., as shown by Fig. 2b and d. In contrast, if there is a gapless point [m(θ) = 0] in HOT region, Fermi arcs can go through this HOT region because Esurface is gapless for some k∥, e.g., as shown by Fig. 2c. In this regard, the gapless point [m(θ) = 0] determines whether the Fermi arcs can go through the higher-order phase region at an angle θ. Thus, strikingly, the Fermi-arc topology changes with θ.

Second, m(θ) in Eq. (4) is antiperiodic. Remarkably, it becomes periodic in the surface spectrum Esurface after taking the square, since the square of m(θ) obeys

$${m}^{2}({{{{\theta }}}})={m}^{2}(\theta +\pi /n),$$
(5)

which has a period of π/n.

The periodic function m2(θ) indicates that the topology of Fermi arcs not only changes with the surface orientation θ, but also in a periodic pattern. We emphasize that the change of Fermi-arc topology comes from the intertwining of unconventional Weyl fermions and higher-order topology. Thus, this phenomenon is absent in any individual phase alone. This is distinct from ref. 59, where the edge states in different samples of different geometry are determined by higher-order topology. Thus, it constitutes the characteristic feature of intertwined Weyl phases.

After figuring out how m(θ) influences the behavior of boundary states on the 2D surfaces, it is also necessary to discuss its impact on the boundary states on the 1D hinges. The hinge states, seen in the HOT phases, are determined by the condition m(θ) = 0. For m(θ) ≠ 0, no localized zero modes can be observed. This is in accordance with the behavior of the HOT phase. Thus, the hinge states of higher-order topology can still be observed in 1D, as shown by the green lines in Fig. 1.

Exemplification of intertwined double-Weyl and triple-Weyl phases

The intertwined double-Weyl phase is generated by the fourfold rotation symmetry C4, i.e., n = 2, as we show previously. The Weyl points carry a monopole charge of ± 2, which emits two Fermi arcs on the surface. According to Eq. (5), on 2D surfaces, the change of Fermi-arc topology is of period π/2. In Fig. 2b–d, we show the topology of Fermi arcs in three representative orientations of θ = 0, θ = π/4, and θ = π/2 in a full period of [0, π/2], respectively. Clearly, by rotating surfaces, the Fermi-arc topology changes from Fig. 2b (θ = 0) to Fig. 2c (θ = π/4), and then returns to the initial topology in Fig. 2d (θ = π/2). On 1D hinges, the boundary states occur at m2(θ) = 0, e.g., θ = nπ/4 with (n = 1, 3, 5, 7). This is in accordance with the boundary states of HOT phase with C4 symmetry, as shown in Fig. 1a.

A similar story applies to the intertwined triple-Weyl phase which is enforced by sixfold rotation symmetry C6, i.e., n = 3. On 2D surfaces, each triple-Weyl point emits three Fermi arcs on the surface, and the topology of Fermi arcs changes periodically with a period of π/3, as shown by Fig. 2e–g in a full period [0, π/3]. On 1D hinges, the boundary states occur at, e.g., θ = nπ/6 with (n = 0, 2, 4, 6, 8, 10). They are in accordance with the boundary states of the HOT phase with C6 symmetry, as shown in Fig. 1b.

Intertwined double-Weyl phase

We now apply our theory to the intertwined double-Weyl semimetals, which can be realized in cold-atom experiments or other artificial systems. The model Hamiltonian reads

$$\begin{array}{ll}H({{{\bf{k}}}})=2A(\cos {k}_{y}-\cos {k}_{x}){\tau }_{3}{\sigma }_{1}+2A\sin {k}_{x}\sin {k}_{y}{\tau }_{3}{\sigma }_{2}\\ \qquad\quad\,\,+\,M({{{\bf{k}}}}){\tau }_{3}{\sigma }_{3}+\epsilon {\tau }_{0}{\sigma }_{3}+m{\tau }_{1}{\sigma }_{1},\end{array}$$
(6)

where \(M({{{\bf{k}}}})={M}_{0}-2t(\cos {k}_{x}+\cos {k}_{y}+\cos {k}_{z})\). The four double-Weyl points are located on the kz axis at kz = ±kw1 and kz = ±kw2, where \({k}_{{{\mbox{w}}}1(2)}=\arccos [(M-(+)\sqrt{{\epsilon }^{2}+{m}^{2}})/2t]\) with M = M0 − 4t. By series expansion around the Weyl points at (0, 0, ±kw1(2)), i.e., \(({k}_{x},{k}_{y},{k}_{z})\to (\delta k\cos \theta ,\delta k\sin \theta ,\delta {k}_{z})\), the form of the low energy model H(k) = Aδke+2iθτ3σ− + Aδke−2iθτ3σ+ + tδkzτ3σ3 + ϵτ0σ3 + mτ1σ1 is the same as Eq. (1). Double-Weyl points are generated by the ϵ term that breaks time-reversal symmetry. They possess monopole charge of ±260,61. mτ1σ1 corresponds to mΓh in Eq. (1), which is responsible for the higher-order topology. The whole system is protected by fourfold rotation symmetry \({\hat{C}}_{4}={\sigma }_{3}{\tau }_{3}\). The Fermi arcs shown in Fig. 2b–d are numerically calculated by using the model (6) with open boundary conditions.

In Fig. 3a, the Chern number in kxky-plane against kz is plotted. Here, without loss of generality, we assume kw2 < kw1, for the chosen parameters given in the caption of Fig. 3. We can see that the Chern number changes by 2 when passing a double-Weyl point. This is because the Chern number on the surface that encloses the Weyl point equals to the monopole charge, as it does for conventional Weyl phases. This explains the non-trivial Chern number between the upper pair kz ∈ (kw2, kw1) and lower pair kz ∈ (−kw1, −kw2) of Weyl points. However, the distribution of the Chern number in the intertwined phase is different from conventional ones. In order to host HOT phases, it is required to have a region where the Chern number vanishes. Here, the region is between the lower and upper pairs of Weyl points, i.e., \({k}_{z}\in \left(-{k}_{{{\mbox{w}}}2},{k}_{{{\mbox{w}}}2}\right)\), as shown by the HOT region (green arrow) in Fig. 3. In this region, the existence of boundary states depends on the orientation θ, as shown by Fig. 3c. In contrast, in the region with non-zero Chern number, i.e., inside the two sets (upper and lower) of Weyl points, the Fermi arcs exist regardless of the angle θ.

Fig. 3: The location of Weyl points and the orientation-dependent mass term.
figure 3

a Left: The four double-Weyl points on the kz axis. Red and blue dots denote Weyl points with monopole charge +2 and −2, respectively. Right: Chern number on kxky-plane against kz, which changes by ± 2 when a double-Weyl point is passed. It is nontrivial within upper and lower two pairs of double-Weyl points. b The higher-order term \(m{(\theta )}^{2}={m}^{2}{\cos }^{2}(2\theta )\) is a periodic function with period π/2. c Angular dependence of Fermi arcs in the range of [0, π/4], which is between Fig. 2b and c. The parameters are A = 1, M0 = 4.5, t = 1, ϵ = 0.2, and m = 0.5.

Full size image

Effective boundary theory

To understand the periodic behavior of Fermi-arc topology, a boundary theory applicable to any surface orientation is constructive. We can achieve this goal by firstly deriving two boundary states for each θ in the absence of the higher-order term mτ1σ1 in Eq. (6). The spinor part of two boundary states takes the form of \({\psi }_{1}\propto ({e}^{-2i\theta },\sqrt{2}+1,0,0)\) approximately in the region of kz ∈ (−kw2, kw2), and \({\psi }_{2}\propto (0,0,{e}^{-2i\theta },\sqrt{2}+1)\) in the region of kz ∈ (−kw1, kw1). Note that the contribution from spatial part of the boundary states does not affect the main results, and is neglected for simplicity. By projecting the whole Hamiltonian into the subspace spanned by the boundary states, we can obtain the effective boundary Hamiltonian as (See Supplementary Note 1 and 2 for derivation details.)

$${h}_{{{\mbox{surf}}}}=-\frac{1}{\sqrt{2}}\left[(2{k}_{\parallel }^{2}-{k}_{\,{{\mbox{c}}}\,}^{2}){\sigma }_{3}-m\cos (2\theta ){\sigma }_{1}\right],$$
(7)

up to a constant term \(-1/\sqrt{2}\epsilon {\sigma }_{0}\), and \({k}_{\,{{\mbox{c}}}\,}^{2}=2t\cos {k}_{z}-M\). Clearly, the boundary Hamiltonian is in the form of Eq. (3). The effective Hamiltonian is valid in the region where ψ1 and ψ2 overlap, i.e., \({k}_{z}\in (-{k}_{{{\mbox{w}}}2},{k}_{{{{\mbox{w}}}}_{2}})\) between the middle two Weyl points, where the Chern number is trivial. On a 1D hinge, the gapless points at \(m\cos (2\theta )=0\) result in hinge Fermi arcs, as shown by the green solid lines in Fig. 1.

On 2D surfaces, clearly, the periodic change of Fermi-arc topology, shown in Fig. 2b–d, is caused by the higher-order term \(m\cos (2\theta )\). The period is π/2, as determined by \({m}^{2}{\cos }^{2}(2\theta )\) in the spectrum, in accordance with the general theory of Eq. (5). Within a single period, the higher-order topology enforces the appearance of gapless point [Eq. (4)], which is located at \(m\cos (2\theta )=0\). The gapless point drastically changes the topology of Fermi arcs, because it determines whether the arcs can go through the region of kz ∈ (−kw2, kw2) between the middle two Weyl points or not. Figure 2b–d shows three representative orientations in a full period of θ ∈ [0, π/2]. The Fermi arcs cannot go through the region between the two middle Weyl points at θ = 0. After rotating to θ = π/4 at the gapless point, the Fermi arcs are allowed to go through. Finally, at θ = π/2, the Fermi arcs return to their initial topology, completing one period.

Guidelines for material search

Two key ingredients of the discussed intertwined Weyl phases are fourfold (sixfold) rotation symmetry and the unconventional Weyl points on the rotation axis. Both requirements can be fulfilled in tetragonal, cubic, or hexagonal space groups, where the desired symmetries emerge. There is a correspondence between the absolute value of the chirality of a crossing and the rotation eigenvalues of the involved bands62, such that a crossing between certain rotation eigenvalues leads to the required unconventional Weyl points. The total phase of eigenvalues accumulated by such crossings for any pair of bands is restricted by the periodicity of Brillouin zone. To be more specific, to obtain crossings of the required charge of ±2 (±3), the phase of the eigenvalues of fourfold (sixfold) rotation must change by π. By looking at Fig. 1 it is evident that intertwined Weyl points require an even number of such changes of the eigenvalue phase. Thus, the necessary crossings can only occur if the total accumulated phase, which is consistent with the periodicity of the Brillouin zone, is equal to \(0\,{{\mathrm{mod}}}\,\,2\pi\), like it is fulfilled in Eq. (6). This excludes for nonsymmorphic systems certain filling factors, where the k-dependence of rotation eigenvalues would, for example, require an odd number of crossings. An appropriate filling b for a 2n-fold rotation with a fractional translation of \(\frac{m}{2n}\) has to fulfill \(\frac{bm}{2n}\in {\mathbb{Z}}\).

Commonly, a set of four crossings like in Fig. 1 would be accidental. Nevertheless, enforced crossings can be found within fourfold degenerate points, e.g., in space groups 106 and 133 on the path M-A. These comprise unconventional Weyl points related by mirror symmetry63. Hereby, mirror pairs of enforced unconventional Weyl points coincide. If a weak time-reversal and mirror symmetry breaking is introduced to such a system, one may obtain Weyl points in the configuration discussed in Fig. 1a with no other enforced bands at the Fermi energy. A comprehensive material search is left for future works.

Cold-atom experimental realization

Owing to technical advances, cold atoms have been widely applied in quantum simulations of topological matter64,65,66,67, and now are also readily available for realizing our intertwined double-Weyl semimetal described by Eq. (6). Here we present the realization proposal using fermionic atoms. We choose two hyperfine states as the pseudo-spins ↑↓ for the σ degrees of freedom. For our model Hamiltonian, which requires two extra degrees of freedom, we consider the atomic gases loaded in a 2D bilayer optical lattice, and thus, the layer index λ is used to represent the τ subspace. The setup is illustrated in Fig. 4. The energy offset of the hyperfine states is prepared as \({{{\Gamma }}}_{\lambda }(\phi )={M}_{0}+{(-1)}^{\lambda }\epsilon -2t\cos \phi\) that is manually controllable by the cyclical parameter ϕ. It not only generates the on-site energy of the model Hamiltonian, but also introduces the additional parameterized space represented by ϕ. In this way, the band physics of the Weyl Hamiltonian can be captured in the 3D parameterized space (kx, ky, ϕ)68. Here, ϕ corresponds to kz in Eq. (6).

Fig. 4: Illustration of experimental setup.
figure 4

The atoms are confined in a bilayer optical lattice. Couplings between opposite pseudo-spins are processed via laser fields of modes M1(r), M2(r), and \(M^{\prime}_{2} ({{{\bf{r}}}})\). The on-site energy offset is prepared as Γλ(ϕ) which not only depends on the layer index but also is manually controlled by the parameter ϕ.

Full size image

In order to engineer the intra-layer spin-flipped hopping, we use laser fields of three modes to couple the pseudo-spins. The spatial modulations of the field modes are prepared as \({M}_{1}({{{\bf{r}}}})=i{M}_{1}\sin ({k}_{{{\mbox{L}}}}x)\sin ({k}_{{{\mbox{L}}}}y)\), \({M}_{2}({{{\bf{r}}}})={M}_{2}\cos ({k}_{{{\mbox{L}}}}x)\cos (3{k}_{{{\mbox{L}}}}y)\cos ({k}_{{{\mbox{L}}}}z)\), and \(M^{\prime}_{2} ({{{\bf{r}}}})=-{M}_{2}\cos (3{k}_{{{\mbox{L}}}}x)\cos ({k}_{{{\mbox{L}}}}y)\cos ({k}_{{{\mbox{L}}}}z)\), where kL = π/d and d denotes the lattice constant. Due to the odd parity of M1(r) in the xy-plane69, the on-site and nearest-neighbor (NN) couplings vanish, while the next-NN coupling dominates, resulting in \(\sin {k}_{x}\sin {k}_{y}{\sigma }_{1}\). Due to the crystalline symmetry, the combination of M2(r) and \(M^{\prime}_{2} ({{{\bf{r}}}})\) leads to the NN coupling \((\cos {k}_{y}-\cos {k}_{x}){\sigma }_{1}\). After making operator transformations, all the intra-layer terms host opposite signs for different layers. Furthermore, the HOT term τ1σ1 is naturally introduced by the inter-layer hopping. The details of the realization proposal are shown in Supplementary Note 3.

Discussion

Based on the theory to create topological phases by intertwining existing ones, we have discovered the intertwined Weyl phase. The intertwined Weyl phase is different from the individual unconventional Weyl semimetallic phase or HOT phase, and exhibits its distinct characteristic topological features. The intertwining results in the drastic change of Fermi-arc topology in a periodic pattern, which constitutes the characteristic feature of the intertwined phase. We have proposed a feasible cold-atom experiment to verify our theory and to realize the intertwined Weyl phases.

Our theory could serve as a guiding principle to generate topological phases based on existing ones. A direct application would be to investigate the intertwining between topological gapless phases with emergent particles other than Weyl fermions and topological crystalline phases, that are protected by the same symmetry28,29,30,70,71.

Finally, we note that Fermi-surface topology is crucial for electronic properties of material. The change of Fermi-arc topology in the intertwined Weyl phases offers a direction of tuning Fermi-surface topology. It would inspire further research on electrical, magnetic, thermodynamic, and transport properties, that are determined by Fermi-surface topology. For instance, a potential application is to investigate the quantum oscillations of Fermi-arc surface states72. These oscillations are periodic against the inverse of magnetic field 1/B. Their frequency F is determined by the Onsager relation F = Φ0/(2π2)As. Here Φ0 = h/2e is the magnetic flux quantum, and As is the Fermi surface cross section. In intertwined Weyl phases, the cross section As depends on the surface orientation θ. As shown in Fig. 3c, by changing θ, one may interpolate between small Fermi surfaces (localized around kw1 and kw2) and extended Fermi surfaces (connecting kw1(2) to −kw1(2)), which must yield a substantial change in the observed quantum oscillation spectra. Thus, the intertwined Weyl phases are expected to have a significant change of quantum oscillations upon rotating surface termination.

Methods

Analytical derivation and symmetry analysis

The derivation of the analytical results makes use of the k ⋅ p methods and symmetry analysis. The numerical calculation is based on tight-binding model and Green’s function method. Details of these derivations are given in the Supplementary Notes 1, 2, and 4. This includes the calculation of Fermi arcs in intertwined double-Weyl semimetals, and the analysis of symmetry for intertwined double-Weyl and triple-Weyl semimetals. The Supplementary Note 3 also contains a detailed discussion of the cold-atom realization of intertwined double-Weyl semimetals.