Introduction

Over the last few decades, the study of various Hall effects has become an important topic in condensed-matter physics. For Hall effect or anomalous Hall effect, it is well known that an external magnetic field or magnetic dopants are necessary to break the time-reversal symmetry1. However, a recent theoretical study predicted that a second-order nonlinear Hall effect can exist in materials with time-reversal symmetry but without inversion symmetry2. Subsequently, the experimental study on bilayer and multilayer WTe2 has validated this prediction in terms of the observed transverse nonlinear Hall-like current with a quadratic current-voltage characteristic3,4. The nonlinear Hall effect arises from the non-vanishing dipole moment of Berry curvature in momentum space, i.e. Berry curvature dipole2. The theoretical predictions of the nonlinear Hall effect in a material can be achieved by calculating the Berry curvature dipole from band structure. Multiple materials5,6,7,8,9,10,11,12,13,14,15,16,17 have been predicted or validated to possess strong nonlinear Hall effect, such as the Weyl semimetals5,6,7,8, the giant Rashba material bismuth tellurium iodine (BiTeI) under pressure10, the monolayer WTe2 and MoTe2 with an external electric field11, and the strained twisted bilayer graphene12 or WSe213,14.

The experimental observations of the nonlinear Hall effect are mainly limited to the two-dimensional systems3,4,14,15,16. It is well known that the twist angle between adjacent layers can be used as a new degree of freedom to modulate the electronic structures of two-dimensional system, which has attracted great attention since the recent discovery of the unconventional superconductivity and correlated state in the twisted bilayer graphene18,19 and twisted bilayer of transition metal dichalcogenides20. Very recently, it was shown that the strained twisted bilayer graphene12 and WSe213,14 present a large nonlinear Hall response. The experimental results demonstrate that there exists a significant nonlinear Hall effect in bilayer WTe23, it is interesting to know how the twist regulates the nonlinear Hall effect in this system.

In this work, we study the nonlinear Hall effect in twisted bilayer WTe2 by using first-principles calculations combined with the semiclassical approach. Multiple twisted bilayer WTe2 structures are constructed, and the twist angles range from 12° to 73°. It is found that the twisted bilayer WTe2 has a more complicated band structure compared to the prefect bilayer system. We choose the twisted bilayer WTe2 with twist angle θ = 29.4° as a typical system, and show that the Berry curvature dipole of twisted bilayer WTe2 can be strongly enhanced.

Results

Twisted bilayer WTe2

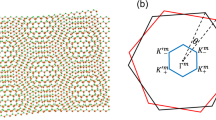
The bilayer WTe2 exhibits an orthorhombic lattice, the optimized lattice constants are calculated to be a1 = 3.447 Å and a2 = 6.284 Å. We construct a series of twisted bilayer WTe2 structures based on the method described in Ref. 21. For simplicity, we start with the normal stacking of perfect bilayer WTe2. As shown in Fig. 1, to construct the twisted bilayer WTe2, a supercell lattice as bottom layer is built, where b1 and b2 are superlattice basis vectors generated by primitive basis vectors a1 and a2. Correspondingly, the supercell basis vectors of top layer share a mirror plane ℳx with bottom layer, which are indicated by \({{{\mathbf{b}}}}_1^\prime\) and \({{{\mathbf{b}}}}_2^\prime\) in Fig. 1. Let b1 = ma1 + na2 and b2 = pa1 + qa2, in which m, n, p and q are integers, then the twist angle satisfies \(\theta = 2\arctan \left( {m\left| {{{{\mathbf{a}}}}_1} \right|/n\left| {{{{\mathbf{a}}}}_2} \right|} \right)\). The twisted bilayer structure is formed by rotating the top layer around the original point by angle θ and translate the top layer by vector b2, while the bottom layer remains fixed. To ensure that the twisted bilayer structure is commensurate, it has to be made sure that b1 is perpendicular to b2. However, this condition is hard to fully meet because of the non-particularity of lattice constants. Approximately, we use a looser condition, for example, the angle between b1 and b2 ranging from 89° to 91° is acceptable. It is important to note that the twist angle will change slightly after structural relaxation. More details on the forming process of twisted bilayer for orthorhombic lattice can refer to Ref. 21.

Fig. 1: Forming process of twisted bilayer.
figure 1

Schematics of the forming process of a twisted bilayer for orthorhombic lattice. a1 and a2 are basis vectors for primitive cell, while b1 and b2 are the supercell basis vectors of the bottom layer, \({{{\mathbf{b}}}}_1^\prime\) and \({{{\mathbf{b}}}}_2^\prime\) are the supercell basis vectors of the top layer before twisting. m, n, p and q are integers, and it is required that b1 is perpendicular to b2.

Full size image

Table 1 gives the optimized twist angle, formation energy and average interlayer distance for our constructed twisted bilayer WTe2. Despite the twist angles ranging from 12° to 73°, these systems share pretty close formation energies and average interlayer distances. It is noted that the interlayer spacing in twisted bilayer WTe2 is corrugated, and the average interlayer distance is slightly larger than that in perfect bilayer system (2.888 Å), suggesting a weakening of interlayer coupling. Besides, the relatively smaller formation energy means that the twisted bilayer WTe2 may form in an efficient way.

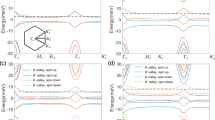
Table 1 Parameters of twisted bilayer WTe2.
Full size table

Compared to the twisted bilayer graphene, the twisted bilayer WTe2 exhibits much more complicated Moiré patterns since one monolayer WTe2 consists of one layer of W atoms and two layers of Te atoms. Figure 2a, b depicts the top and side views of the optimized superlattice for twisted bilayer WTe2 with twist angle θ = 29.4° (the structures with other twist angles are given in Supplementary Fig. 1). Such complicated Moiré superlattice leads to an intricate electronic structure in twisted bilayer WTe2. Take the system with twist angle θ = 29.4° as an example, there exist extensive band anticrossings and band inversions around the Fermi level, as shown in Fig. 2c. With spin-orbit coupling (SOC) being considered, the band structure becomes more intricate, which can be seen from Fig. 2d. Similarly, the band structures with other twist angles also exhibit complicated band structures around the Fermi level, as shown in Supplementary Fig. 2. In our calculations, it is gapless for the constructed twisted bilayer WTe2 systems. However, it is found experimentally that there is small band gap in the twisted bilayer WTe2 for some twist angles22. This inconsistency may be due to the PBE functional underestimating the band gap in band structure calculation. Besides, the difference in the twist angles between calculation and experiment may be another reason for this contradiction.

Fig. 2: Atomic structure and band structure of twisted bilayer WTe2.
figure 2

a, b The Moiré superlattice structure of twisted bilayer WTe2 (θ = 29.4°) in top view and side view, respectively. The red rectangle indicates the supercell. The blue and yellow balls represent W and Te atoms, respectively. c, d The band structure of twisted bilayer WTe2 (θ = 29.4°) without and with SOC, respectively.

Full size image

Giant nonlinear Hall effect

The multiple bands cross or nearly cross in momentum space may bring about large gradient of Berry curvature around the band edges and result in strong nonlinear Hall response2. Next we focus on the twisted bilayer WTe2 with twist angle θ = 29.4°, which possesses the smallest number of atoms in a superlattice, to calculate its Berry curvature dipole and estimate the nonlinear Hall effect.

The Berry curvature dipole Dxz and Dyz of twisted bilayer WTe2 (θ = 29.4°) as a function of the chemical potential are shown in Fig. 3a. For a two-dimensional system, the Berry curvature dipole takes the unit of length. It is noted that in perfect bilayer WTe2 system, due to the presence of ℳy mirror plane, only the y component of Berry curvature dipole is nonzero. However, the introduction of twist can break this symmetry, so the x component of Berry curvature dipole is also nonzero in the twisted bilayer WTe2. It is clear that the Berry curvature dipole Dxz and Dyz exhibit drastic oscillating behavior near the Fermi level, and Dxz and Dyz can switch their signs dramatically within a very narrow energy region. On the other hand, we find that the magnitude of Berry curvature dipole in our considered twisted bilayer WTe2 is much larger than that in previous reports3,4,11,12,13,14,15,16. For example, the peak of Dyz locates near the Fermi level, which is calculated to be ~1400 Å. As a comparison, the Berry curvature dipole in monolayer or bilayer WTe2 is estimated to be in the order of 10 Å3,11, and 25 Å in strained twisted bilayer WSe214, ~200 Å in strained twisted bilayer graphene12, ~700 Å in artificially corrugated bilayer graphene16.

Fig. 3: Nonlinear Hall effect in twisted bilayer WTe2.
figure 3

a The Fermi energy dependence of Berry curvature dipole for twisted bilayer WTe2 (θ = 29.4°). b Band structure and Berry curvature \({\Omega}_{nk,z}\) (Å2) along Γ-Y line. The calculated Fermi level is set to be zero. c, d Berry curvature \({\Omega}_z\) and Berry curvature dipole density dyz along Y-Γ-Y line, respectively.

Full size image

To have a clearly understanding of the features of Berry curvature dipole in the twisted bilayer WTe2, we analyze the band structure and the distribution of Berry curvature. In general, the large Berry curvature appears at the band edge, as displayed in Fig. 3b, where shows the band structure and Berry curvature \({\Omega}_{nk,z}\) along the \({{{\mathrm{{\Gamma}}}}} - {{{\mathrm{Y}}}}\) line. As can be seen from Fig. 3b, the entanglement of multiple bands around the Fermi level causes a complicated distribution of Berry curvature, while the large Berry curvature dipole arises from the drastic change of Berry curvature in momentum space, as indicated by Eq. (2). We find that the peaks of Berry curvature dipole shown in Fig. 3a mainly come from the contribution of the Berry curvature near the band edge shown in Fig. 3b, for instance, the peaks of Berry curvature dipole originate from the band edges at corresponding energy about −0.02, −0.01, 0.0 and 0.02 eV.

When the Fermi level is set to the charge neutral point, we plot the Berry curvature \({\Omega}_z\) and the corresponding density of Berry curvature dipole dyz along the \({{{\mathrm{Y}}}} - {{{\mathrm{{\Gamma}}}}} - {{{\mathrm{Y}}}}\) direction in Fig. 3c, d, respectively. Here, the density of Berry curvature dipole in momentum space is defined as \(d_{bd} = \mathop {\sum}\limits_n {f_{nk}\partial {\Omega}_{nk,d}/\partial k_b}\). Clearly, the Berry curvature and dyz mainly distribute in the region near the Y point, and the tremendous change of Berry curvature contributes large magnitudes to dyz. Furthermore, it is found that the pronounced peaks (marked by “A”) shown in Fig. 3c, d indeed come from the contribution of band edge indicated by the red circle in Fig. 3b. As the Fermi level is shifted from the charge neutral point, the Fermi level go through multiple band anti-crossings in a narrow energy region, leading to the dramatic sign change of Berry curvature dipole around the charge neutral point.

As mentioned above, the Berry curvature dipole in twisted bilayer WTe2 exhibits dramatically oscillating behavior near the charge neutral point. This indicates that the strong nonlinear Hall effect in our considered system may be observed at low temperatures. For clarity, we calculate the temperature dependence of Berry curvature dipole Dyz for twisted bilayer WTe2 (θ = 29.4°) and perfect bilayer WTe2 according to \(D_{yz}(T) = {\int} {D_{yz}(E)\left( { - \partial f/\partial E} \right)} dE\). Here, for simplicity, we fix the Fermi level to the charge neutral point. As shown in Fig. 4, the Berry curvature dipole Dyz of perfect bilayer WTe2 decreases as the temperature raises. This is qualitatively consistent with the experimental result in few-layer WTe24, where the nonlinear Hall response decreases monotonically with increasing temperature. When temperature is larger than 20 K, the Berry curvature dipole Dyz for the twisted bilayer WTe2 (θ = 29.4°) is slightly larger than that in perfect bilayer WTe2. However, the Berry curvature dipole Dyz for the twisted bilayer increases rapidly when temperature is less than 20 K. These results suggest that one could detect a very strong nonlinear Hall response at low temperatures in twisted bilayer WTe2. On the other hand, the Berry curvature dipole in twisted bilayer WTe2 is sensitively dependent on the Fermi level, its magnitude and sign can be switched dramatically within a very narrow energy region. The large magnitude and highly tunable characteristics of Berry curvature dipole in twisted bilayer WTe2 provide an excellent platform to investigate the nonlinear Hall effect.

Fig. 4: Temperature dependence of Berry curvature dipole.
figure 4

The temperature dependence of Berry curvature dipole Dyz for twisted bilayer WTe2 (θ = 29.4°) and prefect bilayer WTe2.

Full size image

Discussion

In this work, we focus on the nonlinear Hall effect in twisted bilayer WTe2 with twist angle θ = 29.4°. It is worth understanding the angle dependence of the nonlinear Hall effect in twisted bilayer WTe2 systems. For comparison, we calculate the energy dependence of Berry curvature dipole for twisted bilayer WTe2 with twist angle θ = 40.1°, the results are shown in Supplementary Fig. 3a. Similar to the system with twist angle θ = 29.4°, the Berry curvature dipole in twisted bilayer WTe2 (θ = 40.1°) also exhibits large magnitude (larger than 1500 Å) and drastic oscillating behavior. However, considering the large computational costs, the nonlinear Hall effect of other twist angle systems is not calculated. Nevertheless, we can make a simple prediction for the features of the nonlinear Hall effect in these systems according to the band structure. For example, there also exist rich band crossings in the case of twist angles θ = 12.3° and θ = 25.7° (see Supplementary Fig. 2). The complicated band structure in a narrow energy region brings about the dramatically oscillating behavior of nonlinear Hall response in these twisted bilayer WTe2 systems. As a comparison, the band structure in the perfect bilayer WTe2 is much simpler (see Supplementary Fig. 2a), and the energy dependence of Berry curvature dipole for perfect bilayer WTe2 is also much smoother (see Supplementary Fig. 3b). Moreover, the entanglement of multiple bands around the Fermi level indicates the drastic change of Berry curvature in momentum space, which may lead to the giant Berry curvature dipole in these twisted bilayer WTe2 systems. Of course, the predictions mentioned above may be not applicable to the small twist angle systems. On the other hand, the contributions to the nonlinear Hall effect can be divided as intrinsic (geometric) and extrinsic (disorder-induced) contributions23. Here, we focus on the intrinsic part of the nonlinear Hall conductivity, which is related to the Berry curvature dipole. However, it is revealed that disorder-induced extrinsic part has more important contribution to the nonlinear Hall effect in some recent works24,25,26. In twisted bilayer systems, the nonuniformity of twist angle across the sample is believed to be the main source of disorder27, which may have pronounced contribution to the extrinsic part of the nonlinear Hall effect. These issues deserve further study.

In summary, we have predicted that a giant nonlinear Hall effect can exist in twisted bilayer WTe2 system. We show that the twist can greatly change the band structure of bilayer WTe2. There exist abundant band anticrossings and band inversions around the Fermi level in the twisted bilayer WTe2, which brings a strong nonlinear Hall signal in this system. The Berry curvature dipole of twisted bilayer WTe2 (θ = 29.4°) can reach up to ~1400 Å, much larger than that in previously reported nonlinear Hall systems. In addition, the nonlinear Hall effect in twisted bilayer WTe2 exhibits dramatically oscillating behavior due to the complicated distribution of Berry curvature around the Fermi level. Our results show that the twisted bilayer WTe2 can become an excellent platform to investigate the nonlinear Hall effect.

Methods

Nonlinear Hall effect

The nonlinear Hall effect originates from the dipole moment of Berry curvature over the occupied states. In a system with time-reversal symmetry but broken inversion symmetry, when an oscillating electric field \(E_c = {{{\mathrm{Re}}}}\{ \xi _ce^{i\omega t}\}\) is applied, a transverse response current \(j_a = {{{\mathrm{Re}}}}\{ j_a^{(0)} + j_a^{(2\omega )}e^{2i\omega t}\}\) can be generated, where \(j_a^{(0)} = \upchi _{abc}\xi _b\xi _c^ \ast\) and \(j_a^{(2\omega )} = \chi _{abc}\xi _b\xi _c\) are rectified current and second-harmonic current, respectively. The nonlinear conductivity tensor \(\chi _{abc}\) is associated with the Berry curvature dipole2 as follows:

$$\chi _{abc}{{{\mathrm{ = }}}} - \varepsilon _{adc}\frac{{e^3\tau }}{{2\hbar ^2(1 + i\omega \tau )}}D_{bd}.$$
(1)

Here, \(D_{bd}\) is the Berry curvature dipole, \(\varepsilon _{adc}\) is the Levi-Civita symbol and \(\tau\) is the relaxation time. The Berry curvature dipole can be written as2

$$D_{bd} = {{\mathop{\sum}\limits_{n}} {{\int\nolimits_{k}}} {f_{nk}\frac{{\partial {\Omega}_{nk,d}}}{{\partial k_b}}} } ,$$
(2)

where \(f_{nk}\) is the Fermi-Dirac distribution function, and \({\Omega}_{nk,d}\) is the d component of the Berry curvature. For a two-dimensional system, only the out-of-plane component (z) of Berry curvature is nonzero, which is given by28

$${\Omega}_{nk,z} = 2i\mathop {\sum}\limits_{m \,\ne\, n} {\frac{{\left\langle n \right|\partial H/\partial k_x\left| m \right\rangle \left\langle m \right|\partial H/\partial k_y\left| n \right\rangle }}{{(E_n - E_m)^2}}} ,$$
(3)

where \(E_n\) and \(\left| n \right\rangle\) are eigenvalues and eigenwave functions, respectively.

First-principles calculations

The first-principles calculations are performed by using the Vienna ab initio simulation package (VASP)29 with the projector-augmented wave potential method30,31,32. The exchange-correlation potential is described using the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) form33. Spin-orbit coupling is taken into account self-consistently. The energy cutoff of the plane-wave basis set is 350 eV. A vacuum region larger than 15 Å is applied to ensure no interaction between the slab and its image. In our optimization, all structures are fully relaxed until the force on each atom is less than 0.02 eV/Å. The Van der Waals interactions between the adjacent layers are taken into account by using zero damping DFT-D3 method of Grimme34. The maximally localized Wannier functions35,36,37 for the d orbitals of W and p orbitals of Te are generated to compute the Berry curvature and Berry curvature dipole. For the integral of Berry curvature dipole, the first Brillouin zone is sampled by very dense k grids to get a convergent result. Considering the large computational cost, we separate the first Brillouin zone into multiple blocks, and the convergence test is carried out independently for each block. For example, some blocks are sampled with the k-point separation of 5 × 10−5 Å−1.