Abstract
The leading order nonlinear (NL) susceptibility, χ3, in a paramagnet is negative and diverges as T → 0. This divergence is destroyed when spins correlate and the NL response provides unique insights into magnetic order. Dimensionality, exchange interaction, and preponderance of quantum effects all imprint their signatures in the NL magnetic response. Here, we study the NL susceptibilities in the proximate Kitaev magnet α-RuCl3, which differs from the expected antiferromagnetic behavior. For T < Tc = 7.5 K and field B in the ab-plane, we obtain contrasting NL responses in low (<2 T) and high field regions. For low fields, the NL behavior is dominated by a quadratic response (positive χ2), which shows a rapid rise below Tc. This large χ2 > 0 implies a broken sublattice symmetry of magnetic order at low temperatures. Classical Monte Carlo (CMC) simulations in the standard K − H − Γ model secure such a quadratic B dependence of M, only for T ≈ Tc with χ2 being zero as T → 0. It is also zero for all temperatures in exact diagonalization calculations. On the other hand, we find an exclusive cubic term (χ3) that describes the high field NL behavior well. χ3 is large and positive both below and above Tc crossing zero only for T > 50 K. In contrast, for B ∥ c-axis, no separate low/high field behaviors are measured and only a much smaller χ3 is apparent.
Similar content being viewed by others
INTRODUCTION
Since the demonstration by Kitaev1 of the existence of a quantum spin liquid state in two dimensions through exact calculations on a honeycomb lattice, there has been an intense experimental search for its realization in real material systems. Aided through insights provided by Jackeli and Khaliullin2 to engineer (bond-dependent) exchange interactions, the materials search has identified several promising systems with prominent attention given thus far to two candidates, the iridium oxides and ruthenium chloride3,4. Despite the presence of a very large exchange energy (of the order of 100 K), these systems do not order down to comparatively low temperatures. When they do order magnetically, the features observed in both microscopic probes such as neutron scattering and macroscopic measurements such as magnetometry and thermal response are highly unusual and contrast dramatically with what is expected from conventional magnets. In their thermal transport5, thermodynamic6 and microwave response7, they provide tell-tale signs as to the presence of fractionalized excitations sought after in Kitaev magnets.
In the proximate Kitaev spin liquid candidate, α-RuCl3 neutron scattering experiments show a low-temperature magnetic excitation spectrum consisting of sharp spin wave peaks and a continuum associated with fractional excitations6,8. A magnetic transition that sets in at 7.5 K where the spins assume a zig-zag chain pattern located in the ab-plane with two neighboring chains being antiferromagnetically aligned9 is also established. Raman scattering studies also reveal unconventional magnetic excitations with a broad continuum whose temperature dependence is apparent over a large scale compared to the magnetic ordering temperature10,11. The linear susceptibility shows a discontinuity in slope12 at TN = 7.5 K and exhibits substantial in-plane anisotropy that persists in the normal state13. The high temperature (T > 150 K) susceptibility is convincingly Curie-like; however, there is an extended intermediate “Kitaev paramagnetic” region6 beyond Tc. The out-of-plane anisotropies are also significant: the susceptibility parallel to the c-axis is nearly an order of magnitude smaller with only a minor signature at the 7.5 K transition. These magnetic signatures are in stark contrast to what is known in conventional 2D (insulating) antiferromagnets14.
In this communication, we report measurements of the nonlinear DC susceptibilities, χ2 and χ3, in α-RuCl3 and illustrate that they probe many key aspects of the proximate Kitaev spin liquid state as well as the zig-zag antiferromagnetic phase. The equilibrium magnetization in any system can be written in the general form:
where the coefficients represent the various order susceptibilities. In particular, the coefficient χ2 is nonzero when time reversal symmetry is broken, while preserving lattice symmetry; for instance15, in ferromagnets.
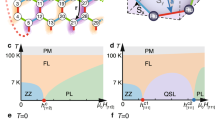
The nonlinear susceptibility χ3 in a classical paramagnet is negative at all temperatures and diverges16 as T → 0, while χ2 is nonexistent due to time-reversal symmetry. The negative divergence in χ3 can be interrupted, however, if the system develops long-range magnetic order. We illustrate in Fig. 1A–C the three known types of characteristic behavior of both the linear (χ1) and the nonlinear (χ2 and χ3) susceptibilities for typical ferromagnets, bipartite antiferromagnets, and spin glasses, respectively15,17,18,19. In all three cases, significant nonzero χ3 is found only in the vicinity of the critical temperature. It is worth noting that χ3 assumes only negative values at T > Tc for all three types of magnets and tends to zero rather quickly as T increases. The second-order susceptibility, χ2, is less studied and a nonzero χ2 is possible only when time-reversal symmetry is either explicitly or spontaneously broken, as in ferromagnets. Moreover, even for bipartite antiferromagnets, an effective time-reversal symmetry due to the sublattice symmetry results in a vanishing χ2 even in the ordered state below Tc; see Fig. 1B.
In the ferromagnet (A) and spin glass (C), the nonlinear susceptibility, χ3, is negative above the characteristic temperature and has a sharp discontinuity at a characteristic temperature (Tc or Tg). In the anti-ferromagnet (B), the sign of χ3 in the paramagnetic regime depends on the coordination number25. Below this temperature, it is observed to rapidly approach zero as T → 0 for all three phases. χ2, on the other hand, exhibits such a discontinuity only for (A) (e.g., ferromagnet) where time-reversal symmetry is broken15. In comparison, in the other two cases it is zero.
In α-RuCl3 we find, in contrast, that χ3 assumes significantly positive values over an extended temperature range above the ordering temperature. While there is a divergence of χ3 at Tc as might be expected, its value remains significantly positive down to the lowest temperatures. We also find a quadratic field dependence of M, giving rise to a significantly positive χ2, which exists only in the ordered state and has a large nonzero value even as T → 0. To our knowledge, such a behavior of χ3 and χ2 have not been observed before. Further, this unexpected quadratic contribution is highly anisotropic and found only when the magnetic field is perpendicular to the high symmetry axis (c-axis).
Results and discussion
Experimental results
In Fig. 2, we show the measured magnetization isotherms for B ∥ a-axis (i.e., ϕ = 0° as per the definition adopted in ref. 13) plotted in a manner that facilitates the extraction of the nonlinear susceptibilities. Equation (1) above defines the susceptibility parameters and motivates plots such as Fig. 2. It is apparent from the top nine panels in Fig. 2 that the slope of the lines for B ∥ a-axis, which are well defined and close to zero at high T, turn significantly positive when lowering T, and increase in magnitude as the ordering temperature Tc = 7.5 K is approached. Below Tc, the response breaks into two distinct regions, with a crossover threshold field of B* ≈ 2 T. The nonlinear response below B* is considerably larger than that at the high field end, 3 T < B < 5 T. Confining ourselves to the quadratic term only, as per Eq. (1) in this low field region, we obtain values of χ2 as shown in Fig. 3b. The values of χ2 are positive and large at the lowest temperatures and decrease monotonically towards Tc, where it rapidly drops to zero. It is important to note that a nonzero χ2 is only possible in systems in which time-reversal symmetry is broken20. In a strict bipartite antiferromagnet, however, time-reversal symmetry is not broken. The fits described above also yield χ1 via the intercept, which can be used as a consistency check on the linear susceptibility values obtained at constant low field through temperature sweeps. The absence of any feature in χ1 in the vicinity of 14 K alludes to the high quality of the sample measured.
The top set of nine panels show the ratio of the measured magnetization, M, to the magnetic field, B, in α-RuCl3 (with B up to 5 T ∥ a-axis) plotted against B. Such a plot provides the quadratic nonlinear susceptibility, χ2, via the slope of the blue straight lines on the low field side. Since at the high field end (B > 3 T) the response is better fit with a cubic term χ3, we show in the nine panels on the bottom a similar plot but with B2 on the abscissa and the fits in orange straight lines. It is clear from these panels that χ3 when B ∥ a-axis is positive over a wide temperature range, while χ2 vanishes for T > TN.
Panel (a) shows the linear susceptibility obtained through temperature sweep (black circles) as well as those obtained from the intercepts of the magnetization isotherms of the χ2 and χ3 analysis such as in Fig. 2 (blue circles). Panel (b) shows χ2 extracted from the low field quadratic response, from plots such as in Fig. 2, top nine panels. Similarly, panel (c) shows the temperature dependence of χ3 obtained from plots such as those in Fig. 2, bottom nine panels. A sharp “lambda”-like anomaly is apparent for χ3 obtained from the high field (3–5 T) response when B ∥ a-axis. The error bars capture the coefficient of determination of the linear fits such as shown in Fig. 2.
Another significant feature notable in the nine panels on the top in Fig. 2 is the presence of a clear upward curvature, in the 3–5 T region, particularly in the 6 and 10 K isotherms. This curvature implies the presence of a cubic term, which can be extracted by plotting M/B against B2 on the x-axis as shown in the bottom nine panels of Fig. 2. The values of χ3 obtained by fitting the linear region in such plots with B between 3 and 5 T below Tc and over the entire field range (0–5 T) above Tc are shown in Fig. 3c. The high linearity of these fits illustrates the absence of a χ2 term in these regions of the phase diagram. Performing such separate fits in the two regions is the most natural way to analyze our results. Our approach of separate fits is further motivated by signs of a crossover transition at ≈2 T in neutron12,21, microwave response7, and differential susceptibility22 experiments.
As can be seen in Fig. 3c, χ3 is significantly positive near Tc and decreases in magnitude as the temperature is increased. A power-law fit as shown in the figure provides a reasonable empirical description of the behavior of χ3 in the (Kitaev) paramagnetic region. Experimentally, however, a crossover to negative χ3 occurs above temperature 50 K (a temperature of the order of the Kitaev exchange6). Below Tc the values of the nonlinear susceptibility are obtained through linear fits in two separate regions as explained above. The high field region yields values for χ3 that exhibit a sharp peak at T = 6.5 K just below the ordering temperature. They remain positive down to the lowest temperature of 2 K with no evidence of a downturn towards zero. While a negative cubic power-law dependence is expected from the Curie law for the third-order susceptibility in paramagnets16, such a positive behavior has not been reported to our knowledge.
We have also measured the nonlinear susceptibility for magnetic fields perpendicular to the ab-plane. Representative magnetization isotherms plotted similar to those in Fig. 2 are shown in Fig. S2. The extracted values of χ3 are small and positive and increase monotonically as the temperature is lowered as seen in Fig. S3. More importantly, as evident in Fig. S2, the nonlinear response is well described by a single cubic term and there is no evidence for a large quadratic response as found for B ∥ a-axis. Given that for B ∥ a-axis the deviation from a linear behavior of the magnetization due to a quadratic contribution is roughly ten times larger than that arising from the cubic term, such behavior if present for B ∥ c-axis would be easily seen within the resolution of the MPMS SQUID measurements. We also present in Fig. S4 preliminary data for the in-plane nonlinear response when B ⊥ a-axis. While the behavior observed is qualitatively the same as in Fig. 3, there are quantitative differences. Further characterization of this in-plane anisotropy will form part of a separate comprehensive study.
Comparison to traditional nonlinear susceptibility responses
Measurements of the equilibrium third-order susceptibility, although rare, have been performed in 2D magnets, frustrated systems, spin glasses, and strongly correlated itinerant metamagnets, that is, materials that show a rapid rise of magnetization at a critical field Bc (see, for example, ref. 23). In a bipartite antiferromagnet such as FeCl224, or even in the classic 2D magnets, (C2H5NH3)2CuCl414, the DC nonlinear susceptibility, χ3, exhibits a “lambda”-like anomaly just below Tc as expected by the theory. From below Tc the standard response of χ3 in these systems is a rapid rise to a large positive value at Tc, above which it drops with the sign being set by the coordination number25. For instance, in the paramagnetic phase of the Kagome system SCGO26, a large positive value of χ3 is seen above Tc, but it reaches close to zero within 2Tc. In many strongly correlated itinerant metamagnets27,28, in which an order parameter develops, χ3 peaks at the ordering temperature and decreases rapidly at T → 0. Nonlinear susceptibility measurements in such systems typically probe higher-order correlations and place strong constraints on the ground state29,30. These latter systems are three-dimensional electronically, but can exhibit a strong magnetic anisotropy due to the g-factor. Nevertheless, in these systems, for all directions it is sufficient to include only the cubic term and the possibility of a dual response with a quadratic term has almost never been discussed (for an exception, see ref. 31). Thus, the features reported above in α-RuCl3 are in contrast to much of what is known about nonlinear susceptibilities in magnets. The unmistakable presence of a large T → 0 quadratic term makes α-RuCl3 a unique 2D quantum antiferromagnet.
Comparison to simulations of the J 1–J 3–K–Γ model
In order to understand the nature of the nonlinear susceptibility in α-RuCl3, it is possible to consider several approaches based on different model Hamiltonians employed thus far13,32. Most of these approaches start with the Kitaev–Heisenberg model appended with various choices of off-diagonal terms33,34. The correct choice of the Hamiltonian is still very much a matter of debate with the sign of the Kitaev term or even the necessity of the Kitaev term being in question35,36,37. We focus on this model and apply two separate calculation tools to study the nonlinear susceptibilities for α-RuCl3: (a) we use CMC simulations with the model Hamiltonian
This so-called J1–J3–K–Γ model is considered one of the the most successful efforts in modeling α-RuCl332. (b) We employ exact diagonalization (ED) methods with slight adjustment on parameters as in ref. 38. For (a), although quantum fluctuations are expected to be strong for such spin-1/2 systems, the fact that the magnet develops a long-range antiferromagnetic order justifies the classical spin approximation, as a first step to understanding the magnetic properties of the ordered phase. For (b), the choice is based on the recognition that it reproduces the magnetization isotherms to high fields very well.
With the CMC simulations we reproduce the phase transition to the so-called zig-zag order at Tc ≈ 0.11 K, where K is the dominant Kitaev exchange constant, with the other parameter values normalized to K taken as Γ = 0.5, J1 = 0.036, J3 = 0.035, ga = gb = 2.3, and gc = 1.339,40. Our calculations of the linear susceptibility χ1 based on the Monte Carlo data, as shown in Fig. 4 (top panel), shows a broad bump near the critical temperature, a feature that is qualitatively consistent with the experiment (Fig. 3a). However, in stark contrast to the experimental data, our simulations find a positive and significant χ2 only in the vicinity of Tc (Fig. 4 -middle panel). Our finding of a vanishing χ2 at very low temperatures in the zig-zag phase is, in fact, consistent with an emergent time-reversal symmetry of the low T-ordered state. To see this emergent symmetry, we first note that although there are three equivalent propagation directions for the zig-zag order, it has been shown experimentally and theoretically that the ground state of α-RuCl3 is a single-Q zig-zag. Spins in such single-Q zig-zag are collinear, with opposite spins sitting on alternating zig-zag chains of the honeycomb lattice. The total magnetization of such collinear bipartite antiferromagnetic order is the sum of the two sublattices: \({\bf{M}}=({M}_{A}+{M}_{B})\ \hat{{\bf{n}}}\), where \(\hat{{\bf{n}}}\) is the collinear spin direction, and 〈MB〉 = − 〈MA〉. Their contributions to the second-order magnetic susceptibility d
cancel each other due to the sublattice symmetry \(\langle {M}_{A}^{3}\rangle =-\langle {M}_{B}^{3}\rangle\) and \(\langle {M}_{A}^{2}{M}_{B}\rangle =-\langle {M}_{B}{M}_{A}^{2}\rangle\). The persistence of the quadratic χ2 down to the lowest temperatures in our experiments thus highlights the unusual nature of the zig-zag order. This intriguing discrepancy could be due to nontrivial quantum fluctuations in the ordered state. Another possible scenario is that the nonzero χ2 results from a highly inhomogeneous multidomain zig-zag order at low temperatures. Indeed, at the interfaces between different zig-zag domains, the two sublattice collinear spins argument given above no longer applies and a nonzero χ2 could result from the complex noncollinear structure at the domain boundaries. Our experiments also imply that the low-temperature χ2 vanishes at the critical field B* ≈ 2 T. Interestingly, this critical field B* has recently been attributed to the so-called Q-flop transition identified both in neutron diffraction12,21 and terahertz spectroscopy41,42. Since the presence of the magnetic field in the ab-plane breaks the equivalence of the three zig-zag orientations, the Q-flop transition describes a repopulation of zig-zag domains in which two energetically unfavorable zig-zag domains are replaced by the third one. Such a realignment of the zig-zag domains also significantly reduces the noncollinear spins residing on the interfaces of different zig-zag order, thus giving rise to a reduced χ2. Detailed numerical simulations of the Q-flop transition and its effects on χ2 will be left for a further computational study. The breaking of the sublattice symmetry, which leads to a nonzero χ2 in the ground state, could also come at the dynamical level, for example, due to nontrivial quantum fluctuations with noncollinear high-order spin correlations in the ordered state27. Other possibilities such as a stacking of the single-Q collinear zig-zag order along the c-direction that breaks the sublattice symmetry cannot be ruled out either. Compared with CMC simulations another intriguing result from our experiments is the persistence of large χ3 in both high- and low-temperature regimes. The values of χ3 from CMC simulations approach zero very rapidly above Tc in contrast to the experimental large and positive values that persist for temperatures significantly greater than Tc. The low-temperature discrepancy of χ3 can be attributed to the absence of quantum fluctuations in CMC.
This figure shows the temperature dependence of the linear and nonlinear susceptibilities obtained in Monte Carlo calculations, for B ∥ a-axis. χ2 (middle panel) rises rapidly to positive values at TC reaches a maximum and drops sharply again below TC. This latter feature is in sharp contrast to the experimental results where the large positive χ2 persists to the lowest temperatures measured. Similar results in contrast to the experiment are obtained for the behavior of χ3. It also attains a positive value below T ≈ 0.11 (in units of K1), reaches a peak value near TN, and rapidly decreases at lower temperatures (lower panel). Note that y-axis scale is arbitrary.
However, the importance of such fluctuations is borne out in similar calculations utilizing quantum chemistry methods discussed below. They are also seen in quantum Monte Carlo simulations in the pure Kitaev limit by Kamiya et al.43, which show a persistent positive χ3 down to the lowest temperatures. In quantum chemistry methods, we use ED of a closely related Hamiltonian employed in ref. 38, which yields accurate results for the magnetization isotherms in good agreement with experimental results at the high field end. The calculated magnetization isotherms in this approach plotted in a manner similar to experiments are well fit with a single straight line (see Fig. S9), implying that only χ3 contributes. The values of χ3 extracted from such calculations are large and positive even at T = 0 (Fig. 5). Also shown in Fig. 5 is the behavior of the calculated derivative d2M/dB2, which displays a zero intercept for all temperatures. This implies that the dual-slope response, which we attribute to the presence of the complex multidomain zig-zag order or other sublattice-symmetry breaking mechanisms, is not found in the ED calculations. It is worth noting that the nonzero value of χ3 for T → 0 is also found in the pure Kitaev model with quantum Monte Carlo calculations43. In such calculations, it is possible to secure a crossover of χ3 at a higher temperature; however, only through the antiferromagnetic Kitaev interaction. Many calculations32 rule out an antiferromagnetic scenario, but our experimental results suggest not to exclude this possibility.
This figure shows the nonlinear susceptibility χ3 in calculations employing exact diagonalization for B in the ab-plane. The results obtained are identical whether B ∥ a-axis or B ⊥ a-axis. χ3 (panel (a)) rises rapidly to positive values at TN reaches a maximum and saturates to a large positive value at T = 0. However, the zero-crossing occurs within 2TN, whereas the experimental zero-crossing occurs at a much higher temperature. Panel (b) shows the second derivative, d2M/dB2, at various temperatures. This derivative passes zero at all temperatures—thus implying the absence of a B2 term in the magnetization contrary to experimental findings.
Moving forward, any viable model for α-RuCl3 must explain the quadratic contribution to the magnetization in the antiferromagnetic zig-zag phase evident in our experiments. Further, it also has to account for the persistence of the large positive values of the third-order susceptibility for temperatures well above Tc. It might be that the details of the material parameters will decide the magnitude and the temperature range over which a positive nonlinearity is stretched.
In summary, we have presented measurements of the nonlinear susceptibility in the Kitaev magnet α-RuCl3. Most significantly, our work has uncovered an anomalous quadratic response of the magnetization to a field that yields a large positive χ2 in the ordered state as T → 0. This behavior is absent when B ∥ c-axis, suggesting a strong 2D nature of the order parameter. This anisotropy as well as the measured anisotropy of χ3 both above and below Tc can serve as future characterization tools for pinning down specific models for proximate Kitaev materials. In addition, our observation of extended positive behavior of χ3 up to 50 K is consistent with previous circumstantial evidence that the Kitaev-type behavior with associated excitations persists up to fairly large temperatures T ≈ 60 K ≫ Tc6,10. The low field crossover, that is, the anomalous response with a quadratic term at low fields does not have to be confined to α-RuCl3 and the generality of its presence in Kitaev or other spin liquid compounds should be established. Furthermore, our results could place constraints on models that attempt to explain experimental observations in α-RuCl3 and similar compounds outside the realm of Kitaev physics35,44. Is the anomalous χ2 and the extended positive χ3 a natural consequence of Kitaev- type models when quantum fluctuations are correctly accounted for or is it a peculiarity of α-RuCl345? We note that the conditions to approach pure Kitaev without the nuisance of magnetic order experimentally are fairly easy to reach—the zig-zag order is destroyed in α-RuCl3 at relatively low pressures of ≈1 GPa46,47. Equally important to carry this work forward will be attempts to predict an in-plane anisotropy of the nonlinear response in a quantitative manner, followed by further detailed experimental work in this regard.
Methods
Materials and experiments
Our measurements were performed on high-quality single crystals similar to those used for recent linear magnetometry measurements13. A Quantum Design Magnetic Property Measurement System SQUID magnetometer capable of reaching 5 T was employed to obtain magnetization isotherms in the temperature range 2–300 K.
Simulations
CMC as well as quantum chemistry-based ED calculations of the linear and nonlinear magnetic response in the K–H–Γ model32 were performed using available packages on a supercomputer.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Hermanns, J. K. M., Kimchi, I. & Knolle, J. Physics of the Kitaev model: fractionalization, dynamic correlations, and material connections. Annu. Rev. Condens. Matter Phys. 9, 17–33 (2018).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018).
Do, S.-H. et al. Majorana fermions in the Kitaev quantum spin system α-RuCl3. Nat. Phys. 13, 1079–1084 (2017).
Wellm, C. et al. Signatures of low-energy fractionalized excitations in α-RuCl3 from field-dependent microwave absorption. Phys. Rev. B 98, 184408 (2018).
Banerjee, A. et al. Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 15, 733–740 (2016).
Banerjee, A. et al. Neutron scattering in the proximate quantum spin liquid α-RuCl3. Science 356, 1055–1059 (2017).
Sandilands, L. J., Tian, Y., Plumb, K. W., Kim, Y.-J. & Burch, K. S. Scattering continuum and possible fractionalized excitations in α-RuCl3. Phys. Rev. Lett. 114, 147201 (2015).
Wang, Y. et al. The range of non-Kitaev terms and fractional particles in α-RuCl3. npj Quantum Mater. 5, 14 (2020).
Sears, J. A. et al. Magnetic order in α-RuCl3: a honeycomb-lattice quantum magnet with strong spin-orbit coupling. Phys. Rev. B 91, 144420 (2015).
Lampen-Kelley, P. et al. Anisotropic susceptibilities in the honeycomb Kitaev system α-RuCl3. Phys. Rev. B 98, 100403(R) (2018).
Narita, N. & Yamada, I. Nonlinear magnetic-susceptibility of two-dimensional magnets (CnH2n.1NH3)2 CuCl4 with n = 1, 2 and 3. J. Phys. Soc. Jpn. 65, 4054 (1996).
Bitla, Y. & Kaul, S. N. Mean-field treatment of nonlinear susceptibilities for a ferromagnet of arbitrary spin. Europhys. Lett. 96, 37012 (2011).
Morin, P. & Schmitt, D. Third-order magnetic susceptibility as a new method for studying quadrupolar interactions in rare-earth compounds. Phys. Rev. B 23, 5936–5949 (1981).
Gingras, M. J. P. et al. Static critical behavior of the spin-freezing transition in the geometrically frustrated pyrochlore antiferromagnet Y2Mo2O7. Phys. Rev. Lett. 78, 947–950 (1997).
Ramirez, A. P., Espinosa, G. P. & Cooper, A. S. Strong frustration and dilution-enhanced order in a quasi-2D spin glass. Phys. Rev. Lett. 64, 2070–2073 (1990).
Suzuki, M. Phenomenological theory of spin-glasses and some rigorous results. Prog. Theor. Phys. 58, 1151–1165 (1977).
Lai, L.-Q., Li, Z., Yu, Y.-B. & Liu, Q.-H. Third-order magnetic susceptibility of an ideal Fermi gas. Commun. Theor. Phys. 70, 619 (2018).
Banerjee, A. et al. Excitations in the field-induced quantum spin liquid state of α-RuCl3. npj Quantum Mater. 3, 8 (2018).
Kubota, Y., Tanaka, H., Ono, T., Narumi, Y. & Kindo, K. Successive magnetic phase transitions in α -RuCl3 : XY-like frustrated magnet on the honeycomb lattice. Phys. Rev. B 91, 094422 (2015).
Shivaram, B. S., Hinks, D. G., Kumar, P., Andrade, M. & Maple, M. B. Universality in the magnetic response of metamagnetic metals. Phys. Rev. B 89, 241107(R) (2014).
Kushauer, J. & Kleemann, W. Critical behaviour of the linear and non-linear magnetic susceptibilities of FeCl2. J. Phys. 7, L1–L6 (1995).
Fujiki, S. & Katsura, S. Nonlinear susceptibility in the spin glass. Prog. Theor. Phys. 64, 1130 (1981).
Schiffer, P., Ramirez, A., Franklin, K. N. & Cheong, S. W. Interaction-induced spin coplanarity in a Kagomé magnet: SrCr9pGa12−9pO19. Phys. Rev. Lett. 77, 2085–2088 (1995).
Ramirez, A. P. et al. Nonlinear susceptibility as a probe of tensor spin order in URu2Si2. Phys. Rev. Lett. 68, 2680–2683 (1992).
Kitagawa, J. et al. Third-order magnetic susceptibility and quadrupolar order parameter of Kondo-lattice compound Ce3Pd2OGe6. J. Phys. Soc. Jpn. 69, 883–887 (2007).
Ramirez, A. P. et al. Nonlinear susceptibility: a direct test of the quadrupolar Kondo effect in UBe13. Phys. Rev. Lett. 73, 3018–3021 (1994).
Bauer, E. D. et al. Nonlinear susceptibility: evidence for antiferroquadrupolar fluctuations and a nonmagnetic Γ1 ground state in the heavy fermion superconductor PrOs4Sb12. Phys. Rev. B73, 094511 (2006).
Zheludev, A. et al. Field-induced commensurate-incommensurate phase transition in a Dzyaloshinskii-Moriya spiral antiferromagnet. Phys. Rev. Lett. 78, 4857–4860 (1997).
Winter, S. M., Riedl, K., Kaib, D., Coldea, R. & Valenti, R. Probing α -RuCl3 beyond magnetic order: effects of temperature and magnetic field. Phys. Rev. Lett. 120, 077203 (2018).
Winter, S. M. et al. Models and materials for generalized Kitaev magnetism. J. Phys. 29, 493002 (2017).
Janssen, L., Andrade, E. C. & Vojta, M. Magnetization processes of zigzag states on the honeycomb lattice: identifying spin models for α-RuCl3 and Na2IrO3. Phys. Rev. B 96, 064430 (2017).
Zhou, Y., Li, Y. D., Yang, X. & Chen, G. Non-Kitaev spin liquids in Kitaev materials. Phys. Rev. B 99, 205119 (2019).
Wilson, E. & Haraldsen, J. Understanding the magnetic interactions of the zig-zag honeycomb lattice: application to RuCl3. https://meetings.aps.org/Meeting/MAR21/Session/E39.11 (2021).
Kim, Y.-J. Ferromagnetic Kitaev interactions and magnetic anisotropy in α-RuCl3. https://meetings.aps.org/Meeting/MAR21/Session/A54.1 (2021).
Yadav, R. et al. Kitaev exchange and field-induced quantum spin-liquid states in honeycomb α-RuCl3. Sci. Rep. 6, 37925 (2016).
Winter, S. M. et al. Breakdown of magnons in a strongly spin-orbital coupled magnet. Nat. Commun. 8, 1152 (2017).
Kim, H.-S. & Kee, H.-Y. Crystal structure and magnetism in α-RuCl3 : An ab initio study. Phys. Rev. B 93, 155143 (2016).
Wu, L. et al. Field evolution of magnons in α-RuCl3 by high-resolution polarized terahertz spectroscopy. Phys. Rev. B 98, 094425 (2018).
Ozel, I. O. et al. Magnetic field-dependent low-energy magnon dynamics in α-RuCl3. Phys. Rev. B 100, 085108 (2019).
Kamiya, Y., Yoshitake, J., Kato, Y., Nasu, J. & Motome, Y. Nonlinear magnetic susceptibility in the Kitaev model. https://meetings.aps.org/Meeting/MAR19/Session/A37.3 (2019).
Modic, K. A. et al. Scale-invariance of a spin liquid in high magnetic fields. Nat. Phys. 17, 240–244 (2021).
Dai, Z. et al. Crystal structure reconstruction in the surface monolayer of the quantum spin liquid candidate α-RuCl3. 2D Mater. 7, 035004 (2020).
Cui, Y. et al. High-pressure magnetization and NMR studies of α-RuCl3. Phys. Rev. B 96, 205147 (2017).
Wang, Z. et al. Pressure-induced melting of magnetic order and emergence of a new quantum state in α-RuCl3. Phys. Rev. B 97, 245149 (2018).
Acknowledgements
We acknowledge many useful conversations with and suggestions for experimental work from Steve Nagler, David Mandrus, and Arnab Banerjee. We are grateful to Jiaqiang Yan for the sample of single-crystal α-RuCl3. We acknowledge useful discussions and correspondence with Pradeep Kumar, Yoshitomo Kamiya, Joji Nasu, Nandini Trivedi, Collin Broholm, and Mike Zhitomirsky. S.N. thanks U. Nitzsche for technical assistance. Z.F. and G.-W.C. are partially supported by the Center for Materials Theory as a part of the Computational Materials Science (CMS) program, funded by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences, and Engineering Division. This work was also partially supported by ONR under the Naval Research Laboratory base program. The work of B.S.S. was supported by NSF Award DMR-2016909 and in. Germany was supported by DFG through SFB 1143 project A05.
Author information
Authors and Affiliations
Contributions
L.H. and J.P. collected the data. L.H. and B.S.S. analyzed the data and made the plots. Z.F. and G.-W.C. performed the classical Monte Carlo simulations. S.N. and J.v.d.B. calculated the magnetization through exact diagonalization of the Hamiltonian. M.O., B.S.S., and G.-W.C. planned the research and developed the manuscript, which was edited by all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Holleis, L., Prestigiacomo, J.C., Fan, Z. et al. Anomalous and anisotropic nonlinear susceptibility in the proximate Kitaev magnet α-RuCl3. npj Quantum Mater. 6, 66 (2021). https://doi.org/10.1038/s41535-021-00364-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00364-z