Abstract
The magnetic ground state of the pyrochlore Yb2GaSbO7 has not been established. The persistent spin fluctuations observed by muon spin-relaxation measurements at low temperatures have not been adequately explained for this material using existing theories for quantum magnetism. Here we report on the synthesis and characterisation of Yb2GaSbO7 to revisit the nature of the magnetic ground state. Through DC and AC magnetic susceptibility, heat capacity, and neutron scattering experiments, we observe evidence for a dynamical ground state that makes Yb2GaSbO7 a promising candidate for disorder-induced spin-liquid or spin-singlet behaviour. This state is quite fragile, being tuned to a splayed ferromagnet in a modest magnetic field μ0Hc ~ 1.5 T.
Similar content being viewed by others
Introduction
The initial proposal1 of quantum spin ice2 behaviour in the pyrochlore Yb2Ti2O7 has ignited a plethora of experimental and theoretical studies of Yb3+ magnetism in various frustrated geometries3,4,5,6,7,8,9,10,11,12,13,14. While there have been many candidates for unusual magnetic ground states in other rare-earth pyrochlore systems, some members of this family, including Yb3+ and Ce3+-based systems, are particularly attractive because quantum fluctuations can be enhanced by their effective spin-\(\frac{1}{2}\) degrees of freedom arising from a Kramers doublet single-ion ground state that is well-separated from excited crystal field levels15,16,17,18,19,20. One less-studied compound within the Yb3+ pyrochlores is Yb2GaSbO7, with its non-magnetic B-site containing a mixture of Ga3+ and Sb5+ cations. Mixed site pyrochlores were originally studied by the chemistry community21,22,23,24,25 and have recently generated interest among condensed matter physicists26,27,28,29,30. A comparison of muon spin relaxation and Mössbauer spectroscopy experiments on Yb2GaSbO7 and Yb2Ti2O7 revealed that, while Yb2Ti2O7 had a dramatic change in the relaxation rate of four orders of magnitude near TC = 240 mK, Yb2GaSbO7 remained dynamic down to a relaxation rate plateau near T* = 340 mK31. This change in relaxation rate for Yb2Ti2O7 has largely been explained32 but the persistent spin fluctuations in Yb2GaSbO7 still remain a mystery. Naïvely, one would assume that the chemical disorder on the B-site would induce a spin-glass state in the latter compound due to the presence of different nearest neighbour exchange pathways. However, the muon decay asymmetry for Yb2GaSbO7 does not follow the typical functional form for a spin glass with only a single exponential relaxation component down to 50 mK, while no low-temperature transitions were noted in both the specific heat31 and Ga-NMR33.
In this work, we provide experimental evidence for a dynamical magnetic ground state in Yb2GaSbO7 and propose possible explanations for this unusual behaviour. We also construct a comprehensive phase diagram for Yb2GaSbO7 using a combination of AC and DC magnetic susceptibility, heat capacity, and neutron scattering. A modest applied magnetic field μ0Hc ~ 1.5 T induces an XY splayed ferromagnetic state, similar to the zero-field ground state observed in pristine Yb2Ti2O7 samples34,35,36,37,38,39. In magnetic fields below μ0Hc, however, neutron scattering experiments reveal spin correlations building up upon cooling that can be characterised with a net antiferromagnetic exchange. A key difference between Yb2Ti2O7 and Yb2GaSbO7 is the presence of net antiferromagnetic exchange, reflected by a concomitant change in sign of the Curie–Weiss temperature in the susceptibility (θCW = −1.42 K in Yb2GaSbO7 compared to θCW = 0.59 K in Yb2Ti2O7)40. Our data suggest that Yb2GaSbO7 in zero field may be close to a phase boundary in the nearest neighbour (n.n.) anisotropic exchange phase diagram for pyrochlore magnets41.
Results
Yb3+single ion properties
We begin our discussion of Yb2GaSbO7 with the single-ion properties of the magnetic Yb3+ ions. We first estimated the crystal field parameters for Yb2GaSbO7 using the scaling analysis procedure42 that has been employed successfully for many other pyrochlore systems. The crystal field parameters used for the scaling were the fitted values for Yb2Ti2O7 in Table 1 from ref. 16. The Yb2GaSbO7 crystal field parameters, eigenfunctions, and eigenvalues obtained from this scaling analysis are presented in Supplementary Tables 1 and 2. We obtain a thermally-isolated crystal field ground state doublet with XY anisotropy for Yb2GaSbO7 with gz = 2.00, gxy = 3.75, and a powder-averaged \(g^{\prime} =3.27\), suggesting that the single-ion properties for this system are similar to other Yb3+ pyrochlores. The gz, gxy, and \(g^{\prime}\) values yield a crystal field moment \({\mu }_{{\rm{CEF}}}=\sqrt{{({g}_{{\rm{z}}}/2)}^{2}+{({g}_{{\rm{xy}}}/2)}^{2}}=2.13\,{\mu }_{{\rm{B}}}\) and an effective moment \({\mu }_{{\rm{eff}}}=\frac{\sqrt{3}}{2}g^{\prime} =2.83\,{\mu }_{{\rm{B}}}\). The latter compares favourably to both the value of 3.04(5) μB (μ0H = 0.1 T, Supplementary Table 3) and the previously reported value31 of 3.15(5) μB (μ0H = 0.004 T), with both values obtained from fitting the low-temperature DC magnetic susceptibility.
Inelastic neutron scattering data were also collected on the neutron spectrometer SEQUOIA at ORNL in an effort to refine the crystal field parameters for Yb2GaSbO7. While this data confirmed that the ground state doublet was well-isolated from the first excited state at 72 meV (see Supplementary Fig. 2), the B-site mixing led to a broadening of the crystal field excitations that hindered the ability of conventional models to account for the data. This broadening in energy is consistent with the presence of disorder in the local environment surrounding the Yb3+ ions, as has been previously observed in Tb2Sn2−xTixO727. This disorder also likely causes a distribution in the strength of the magnetic interactions between neighbouring Yb3+ ions. Notably, the energy broadening observed here prevents us from resolving the two lowest crystal field excitations, which instead yield a single energy peak in the data. This finding is quite different from inelastic neutron scattering results reported previously for defective (i.e. stuffed) single crystalline Yb2Ti2O716, which shows only slightly broader crystal field excitations compared to stoichiometric powder samples. Therefore, the disorder induced by the mixed B-site in Yb2GaSbO7 is much larger as compared to other Yb pyrochlores.
Initial characterisation of zero-field ground state
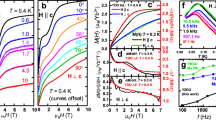
Now that the single-ion properties have been discussed for Yb2GaSbO7 and significant disorder has been established in this system, we turn to its cooperative (collective) magnetic properties. A summary of the AC susceptibility data is presented in Fig. 1. A clear peak is observed at T* = 350 mK in the zero-field data shown in Fig. 1a, coinciding with the plateau of the relaxation rate previously observed in muon spin-relaxation measurements31. Notably, the temperature of the peak maximum exhibits no frequency dependence, in sharp contrast to expectations for a spin glass. An advantage of the in-house instrument used to measure the AC susceptibility is its ability to capture higher-order harmonics43,44, providing another useful way to identify the origin of phase transitions. For example, a paramagnetic to spin-glass transition would only show odd-order harmonics, while ferromagnetic transitions would exhibit both even and odd order harmonics43. Therefore, the presence of the second harmonic shown in Fig. 1c provides additional support that the cusp does not arise from a conventional spin-glass transition. Figure 1b, d show the zero-field ground state observed here is fragile, as small DC fields rapidly suppress both the temperature of the cusp and the strength of the second harmonic signal.
The in-phase component of the first harmonic \({\chi }_{0}^{t^{\prime} }\) for (a) various driving frequencies with a DC field of zero and (b) various DC fields with a driving frequency of 500 Hz. The in-phase component of the second harmonic \({\chi }_{1}^{t^{\prime} }\) for (c) various driving frequencies with a DC field of zero and (d) various DC fields with a driving frequency of 500 Hz. The amplitude of the AC field, μ0H0, is 2.5 × 10−4 T in all cases.
To search for evidence of a thermodynamic phase transition near 350 mK, the heat capacity of Yb2GaSbO7 was measured down to 50 mK (Fig. 2). A low-temperature upturn from a nuclear Schottky anomaly45 arising from hyperfine splitting experienced by a small fraction of Yb3+ nuclear spins was found in the raw data and it has been subtracted off here (see Supplementary Note 3 and Supplementary Fig. 3). The magnetic specific heat Cmag, plotted in Fig. 2b for both 0 and 3 T, was isolated by subtracting off the normalised lattice contribution of Lu2GaSbO7. The entropy release was then obtained by integrating Cmag/T as a function of temperature and is shown in Fig. 2c. Notably, only 87% of the expected Rln(2) entropy is recovered in zero field up to 25 K (see Supplementary Note 3 and Supplementary Fig. 4), although the missing entropy returns by applying a 3 T field. A comparison of the heat capacity measurements on polycrystalline Yb2GaSbO7 and Yb2X2O7 (X = Ge, Pt, Ti, Sn)46,47,48,49,50 is presented in Fig. 2d. No sharp anomaly that is expected for a long-range ordering phase transition is visible in the Yb2GaSbO7 data. Instead, there is a very weak feature present at a temperature comparable to the AC susceptibility cusp, as shown in Fig. 2d and Supplementary Fig. 3a. However, the broad feature observed in the heat capacity data of other Yb3+ pyrochlores and generally attributed to the build-up of spin fluctuations is also apparent here. For Yb2GaSbO7, this feature is centred at 2.3 K in zero field, which is very similar to the value of 2.4 K found for Yb2Pt2O7 (a = 10.09 Å)48. This observation is consistent with previous literature that has established a correlation between the temperature scale of this broad heat capacity feature and the lattice constant of Yb3+ pyrochlores4. Notably, this broad feature is apparent in the heat capacity data over the entire field range measured (0–9 T) and it shifts up in temperature with increasing field as shown in Supplementary Fig. 3c.
a Heat capacity of Yb2GaSbO7 in zero field and an applied field of 3 T, with the lattice standard Lu2GaSbO7 plotted for comparison. b Magnetic component of Yb2GaSbO7 specific heat plotted as Cmag/T. c Entropy release as a function of temperature. d Comparison of Cmag for Yb2GaSbO7 and other Yb3+ pyrochlores46,47,48,49,50. The composition of the B-site is indicated in the panel legend. Note the lack of a sharp lambda anomaly in the Yb2GaSbO7 data.
In zero applied magnetic field, the presence of residual entropy and the lack of a sharp anomaly in the specific heat suggest that the Yb2GaSbO7 ground state may be magnetically disordered. This is borne out by our elastic neutron scattering experiments on the HB-1A instrument at ORNL, which found no magnetic signal at k = 0 positions down to 70 mK (Supplementary Fig. 5), and by our polarised neutron scattering measurements on the D7 diffuse scattering diffractometer discussed below. In particular, the latter measurements show neither new magnetic Bragg peaks, nor depolarisation of the incident beam that would result from weak ferromagnetic ordering.
Field-induced magnetic order
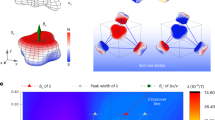
Complementary DC magnetic susceptibility and HB-2A neutron diffraction measurements presented in Fig. 3, and Supplementary Figs. 6 and 7, probed the evolution of the magnetic ground state in applied magnetic fields. It is worth noting that the diffraction data in both zero and applied fields are well-explained by a structural model where the B-site is randomly occupied by a 1:1 ratio of Ga3+ and Sb5+ and no additional nuclear Bragg peaks that would be indicative of long-range charge ordering are observed. Below a critical field μ0Hc ~ 1.5 T, the susceptibility data show Curie–Weiss behaviour down to 2 K, while the diffraction data reveal no magnetic Bragg peaks down to 1.2 K. By contrast, in applied magnetic fields greater than μ0Hc, a net moment develops in the susceptibility measurements and k = 0 magnetic Bragg peaks appear in the neutron diffraction data. The k = 0 magnetic structures allowed by symmetry have been discussed several times for the pyrochlore family15,17,51 and they were all considered in the present case; more details are provided in Supplementary Tables 4 and 5. The best refinement of the 2 T data corresponds to a magnetic structure associated with the Γ9 irreducible representation that has been identified as the zero-field ground state in many other Yb3+ pyrochlores34,35,36,37,48,50,52. To highlight the magnetic portion of the refinement, we have plotted the difference of the diffraction profiles collected at 2 T and 0 T in Fig. 3c. We find an ordered Yb3+ moment of 1.4(1) μB and a spin canting angle (relative to the global [001] direction) of ~−11∘. We note that the negative canting angle indicates that the moments move away from their respective local 〈111〉 directions. This magnetic structure is consistent with the net moment observed in the DC susceptibility measurements and arises from a splayed XY ferromagnet, which is the same magnetic structure reported previously for Yb2Sn2O750. A schematic of this spin configuration is presented in Fig. 3d.
a DC magnetic susceptibility data of Yb2GaSbO7 for various applied fields. Note the development of a net ferromagnetic moment as the field is increased. b Powder neutron diffraction data from HB-2A for Yb2GaSbO7 measured at T = 1.2 K in zero field. The red curve represents a Rietveld refinement of the data to the pyrochlore structure. No magnetic Bragg peaks are visible in this data. c 2 T −0 T difference plot of the T = 1.2 K neutron powder diffraction data, which ensures that the field-induced magnetic scattering can be isolated. A Rietveld refinement using the Γ9 canted ferromagnetic structure is superimposed on the data. Uncertainties in the data are derived from Poisson statistics and represent one standard deviation normalised by the detector efficiency correction. d A schematic of the canted ferromagnetic structure, with the inset depicting the spin arrangement on a single tetrahedron.
Evidence for a dynamical ground state in zero field
Low-energy inelastic neutron scattering and polarised neutron diffraction experiments provide additional insight into the nature of the zero-field ground state for Yb2GaSbO7. Inelastic data were collected on the disc-chopper time-of-flight spectrometer DCS at NIST and are plotted in Fig. 4a. The scattering is broad in energy and Q at all measured temperatures. At small values of Q ~ 0.3 Å−1, the low-energy spectral weight increases with decreasing temperature, suggesting mode softening. Diffuse magnetic scattering data were also measured on the polarised diffuse scattering spectrometer D7 at the ILL, using the 6 pt. xyz-polarisation analysis method53 to separate out contributions from nuclear coherent, nuclear spin incoherent, and magnetic scattering to the total cross-section (see Supplementary Fig. 8). We focus on the magnetic scattering in the discussion that follows. These data are not energy resolved and effectively integrate the magnetic scattering over energy transfers up to λ. Figure 4b compares the energy-integrated D7 data with the inelastic DCS data integrated over 0.15 ≤ E ≤ 1.50 meV at approximately 50 mK; both datasets were independently converted into absolute intensity units by normalising to the nuclear Bragg scattering in each case. The close agreement between the inelastic DCS data and the energy-integrated D7 data suggests that the magnetic scattering is predominantly inelastic at low temperature. The Yb3+ magnetic moment was further obtained through the zeroth total moment sum rule54,
where \({\left(\frac{2}{\gamma {r}_{{\rm{o}}}}\right)}^{2}\) is 13.77 sr b−1, f(Q) is the Yb3+ isotropic magnetic form factor, and μeff is the effective magnetic moment. Integrating the magnetic double differential cross-section over energy and 0.3 ≤ Q ≤ 2.0 Å−1 yields an effective Yb3+ total moment of μeff = 3.13(5)μB from D7 and a dynamic moment of 3.10(2)μB from DCS, with both values in clear agreement with the value of 3.04(5) μB obtained from fitting our 0.1 T DC susceptibility data to a Curie–Weiss law between 2 and 15 K. While this comparison may be affected by systematic differences between measurements on two different instruments, the close agreement between the total and dynamic moments strongly suggests that the scattering at base temperature is mainly inelastic. In particular, the fraction of inelastic scattering is significantly enhanced compared to the value of \(\frac{1}{{J}_{{\rm{eff}}}+1}\) = 67% expected for a Jeff = 1/2 ordered or spin-glass state55,56.
Colour contour plots of the neutron scattering intensity measured on the DCS at (a) 50 mK, 1 K, and 10 K. b Comparison of the normalised scattering intensity measured on DCS to the magnetic cross-section measured on D7 at ~50 mK. c Magnetic differential cross-section data from D7 and (d) the associated nearest neighbour and next-nearest neighbour spin correlations extracted from the fits shown in panel (c) and described in the main text. The temperature of the AC susceptibility cusp measured in zero DC field, TAC, is indicated as a reference. For the purposes of clarity, a vertical offset of 0.2 b sr−1 (Yb3+)−1 has been introduced for each successive temperature in (c). e Calculated fits of the imaginary part of the Q-integrated ([0.5, 2.0] Å−1) dynamic magnetic susceptibility to the damped harmonic oscillator model60 (Eq. (2)) with (f) the temperature dependence of its corresponding fitted parameters: Γ and ωo, defining the peak width and centre, respectively. Uncertainties in the data are statistical in origin and represent one standard deviation, while uncertainties in the fit parameters represent standard error.
To understand the equal-time spin correlations of Yb2GaSbO7, we performed reverse Monte Carlo (RMC) refinements of the magnetic diffuse scattering measured on D7 at temperatures of 55 mK, 1.2 K, 5.0 K, and 10.0 K. The RMC approach fits configurations of magnetic moments Si directly to experimental data without assuming a model of the underlying interactions57,58. Refinements were performed using 3 × 3 × 3 supercells of the crystallographic unit cell and initialised with random moment orientations. At each temperature, two refinements were performed: the first assumed XY moments, while the second placed no constraints (Heisenberg) on the moment distribution. The calculated g-tensor anisotropy is intermediate between Heisenberg and XY limits; however, both limits yielded similar results and so we did not consider the intermediate case. Figure 4c shows fits to data and Fig. 4d shows the temperature dependence of the n.n. and next nearest neighbour (n.n.n.) magnetic correlation functions. The values have been normalised such that 〈S(0) ⋅ S(r)〉 = 1 if all moment pairs separated by distance r were parallel. The equal-time correlations are weakly antiferromagnetic for n.n. and n.n.n.’s at base temperature, but are extremely weak at all measured temperatures—approximately an order of magnitude smaller than for a frustrated classical Heisenberg pyrochlore antiferromagnet at low temperature, where a value of −1/3 would be obtained at the n.n. distance59. This simulation result is obtained because the Q-dependence of the data deviates only slightly from the square of the magnetic form factor, and is unaffected by the possible magnetic anisotropy. Taken together with the large inelastic spectral weight, it appears consistent with a significant role of quantum fluctuations. From our combined DCS and D7 results, we can ascertain that Yb2GaSbO7 has a predominantly dynamical magnetic ground state in zero field.
To understand further the dynamic properties of Yb2GaSbO7, we consider the imaginary part of the dynamic magnetic susceptibility. We obtain this quantity from our inelastic DCS data as \({\chi }^{\prime\prime} (\omega )\propto [1-\exp (-\beta \hslash \omega )]\int I(Q,\omega )dQ\), where the Q integral was taken over 0.5 ≤ Q ≤ 2.0 Å−1. A peak at non-zero energy transfer is observed at all measured temperatures in χ″(ω), as shown in Fig. 4e. Successful fitting of the data to the damped harmonic oscillator (DHO) model given by60
confirmed that this mode is underdamped at all temperatures. The temperature dependence of the fitted mode energy ω0 and relaxation rate Γ are both shown in Fig. 4f. The presence of an underdamped mode over a wide temperature range is reminiscent of a singlet-triplet excitation61, suggesting the intriguing possibility that chemical disorder drives a random-singlet phase in Yb2GaSbO762,63. Notably, there is no apparent change in the dynamic response measured by neutrons as the 350 mK peak in AC susceptibility is traversed, and the majority of the spectral weight remains inelastic below 350 mK, as discussed above. These results suggest that this AC susceptibility peak may be generated by only a small fraction of the spin system freezing, so that the majority of the spectral weight remains unaffected.
Discussion
Our experimental results for Yb2GaSbO7 are summarised in the field-temperature phase diagram presented in Fig. 5. The phase boundaries were obtained from AC susceptibility (temperature of the peak/cusp maximum observed in the in-phase component of the first harmonic), DC susceptibility (temperature of the minimum in \(\frac{d{\chi }_{{\rm{DC}}}}{dT}\)), heat capacity (temperature of the broad anomalies), and neutron scattering data from WAND (temperature of increased intensity for order parameter scans of the (113) magnetic Bragg peak, see Supplementary Fig. 9 for some representative data). At first glance, the phenomenology of Yb2GaSbO7 is very similar to Yb2Ti2O7, as some samples of the latter64 and Yb2GaSbO7 both host a field-induced Γ9 long-range ordered state and a dynamic, correlated phase in zero field at low temperatures. However, there is now a growing amount of experimental evidence that pristine samples of Yb2Ti2O7 exhibit a splayed ice-like ferromagnetic state at low temperatures even in zero field34,35,36,37. The nature of this ordering is extremely sensitive to chemical disorder, specific details of sample preparation/single crystal growth, and "stuffing” effects65. Very recent neutron scattering measurements39 suggest that this extreme sensitivity to disorder may arise from the close proximity of Yb2Ti2O7 to the Γ5 antiferromagnet - Γ9 canted ferromagnet phase boundary of the theoretical phase diagram for the n.n. anisotropic exchange Hamiltonian on the pyrochlore lattice41. Additional evidence supporting the proximity of Yb2Ti2O7 to a phase boundary comes from systematic studies of the magnetic ground states of other Yb3+ pyrochlores, as the ordered spin configuration evolves from a Γ9 canted ferromagnet to a Γ5 antiferromagnet with increasing chemical pressure17. The closest chemical analogue to Yb2GaSbO7 in terms of the lattice constant, and therefore spatial separation between neighbouring Yb3+ ions, is Yb2Pt2O748,66. Interestingly, the in-phase, first harmonic component of the AC susceptibility exhibits a cusp with a clear frequency dependence and the specific heat shows a sharp anomaly; both features are centred at 0.3 K in zero field. These results clearly establish that Yb2Pt2O7 has a canted ferromagnetic ground state similar to pristine samples of Yb2Ti2O7, although the precise spin configuration for the platinate has not been determined.
Shaded regions include a paramagnet (PM), an XY splayed ferromagnet (LRO SFM), a correlated, dynamic phase (DYN) and a regime with minority spin freezing (MSF). The inset depicts an enlarged version of the low-temperature, low-field portion of the phase diagram. The points on the phase diagram were derived from fitting the relevant features of the respective datasets to simple functions, and the error bars for the points correspond to the standard errors from these fits.
We suggest two plausible explanations for the drastic difference in the magnetic behaviour of Yb2GaSbO7, compared to Yb2Ti2O7 and Yb2Pt2O7, despite the similar lattice constant of the latter. First, the intrinsic chemical disorder of Yb2GaSbO7 is likely to generate correspondingly larger disorder in exchange couplings. Intriguingly, this does not cause a conventional spin-glass transition here; instead, our inelastic results are consistent with excitations from a random-singlet ground state. Second, the suppression of conventional magnetic ordering may arise from a fine-tuning of the n.n. superexchange pathways due to the difference in the B-site ions, such that this system is closer to the Γ5-Γ9 phase boundary than any other Yb3+ pyrochlore magnet studied previously. Multiphase competition has also been discussed for Er2Pt2O751, and therefore this phenomenon appears to be a hallmark of many XY pyrochlores. These two effects are not mutually exclusive, and it is possible that disorder and magnetic interactions conspire here to suppress conventional long-range magnetic order or spin-glass formation.
There are intriguing similarities between the behaviour of Yb2GaSbO7 and the triangular-lattice quantum-spin-liquid candidate YbMgGaO4, in which frustration and chemical disorder are implicated in the behaviour of effective spin-\(\frac{1}{2}\) Yb3+ ions6,67. Notably, YbMgGaO4 also shows a low-temperature peak in AC susceptibility68 that is accompanied by a plateau in the spin-relaxation rate obtained in μSR measurements69; however, inelastic neutron scattering measurements below this transition suggest that, at most, only a small fraction of the spins are frozen70,71. These commonalities hint at a common mechanism for spin-liquid-like behaviour in both materials.
In summary, we present evidence for persistent spin dynamics in Yb2GaSbO7 down to 50 mK, which makes this material an intriguing candidate for spin-liquid or frustrated random-singlet behaviour. While the magnetic properties of Yb2GaSbO7 exhibit some similarities to other Yb3+ pyrochlores, the key difference is the lack of magnetic order for Yb2GaSbO7 down to mK temperatures in the absence of an applied magnetic field. Although single crystals may be difficult to obtain due to the volatile nature of the chemical constituents, inelastic neutron scattering on single crystalline Yb2GaSbO7 is highly desirable. The nature of the dynamical ground state could be fully explored with a zero-field measurement. Furthermore, an experiment in the field-induced ordered state would establish the magnetic Hamiltonian for this material, which is essential information for assessing its proximity to a phase boundary in the theoretical phase diagram for rare earth pyrochlore magnets.
Methods
Sample Preparation
Polycrystalline samples of Yb2GaSbO7 and a non-magnetic mixed B-site lattice standard analogue Lu2GaSbO7 were both synthesised by a standard solid state reaction of RE2O3 (RE = Yb or Lu), Ga2O3, and Sb2O5, as previously reported by Strobel et al.22.
Rietveld refinement of the room-temperature laboratory x-ray diffraction pattern confirmed the presence of single-phase pure RE2GaSbO7 (RE = Yb or Lu), possessing \(Fd\bar{3}m\) symmetry with no discernible impurities. The refined room-temperature lattice constant of a = 10.1047(1) Å for Yb2GaSbO7 agrees with previously reported values22,72. A representative x-ray diffraction profile for Yb2GaSbO7 with its corresponding Rietveld refinement superimposed onto the data is presented in Supplementary Fig. 1.
Bulk characterisation
The field and temperature dependence of the magnetisation of polycrystalline Yb2GaSbO7 was measured using a 9 T Dynacool Physical Property Measurement System (PPMS) (The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.) employing the vibrating sample magnetometer (VSM) option. The heat capacity of Yb2GaSbO7 and its corresponding lattice analogue Lu2GaSbO7 were first measured down to 350 mK with the 3He option on a 9 T PPMS from Quantum Design, while subsequent measurements employed the dilution refrigerator (DR) option to access a base temperature of 65 mK.
The AC susceptibility of polycrystalline Yb2GaSbO7 was collected with a warming rate of 7.6 mK/min in a zero-field-cooling (ZFC) process at the National High Magnetic Field Laboratory (MagLab) in Tallahassee, Florida using an in-house set-up44 that facilitated the measurement of both the linear and non-linear components. The raw data (voltage signal) was normalised to both the driving frequency and AC field strength. In general, the magnetisation of a material (with μ0 set to 1) can be expressed as43,44:
Applying an AC magnetic field H = H0sin(ωt) induces a voltage E in the pick-up coil given by:
where A is a numerical factor that depends on the coil dimensions and the filling factor of the sample, and:
\({\chi }_{0}^{{\rm{{t}}}}\), \({\chi }_{1}^{t}{H}_{0}\), and \(3/4{\chi }_{2}^{t}{H}_{0}^{2}\) represent the first, second, and third harmonics that we measure. When the applied AC field is small, the first harmonic is essentially equivalent to the linear AC susceptibility χ0.
Neutron scattering
High energy inelastic neutron scattering (INS) measurements were performed on the direct-geometry time-of-flight chopper spectrometer SEQUOIA73 of the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory (ORNL). Yb2GaSbO7 powder was loaded in a cylindrical Al can, cooled to a base temperature of 5 K using a closed cycle refrigerator, and a powder-averaged (Q, E) spectrum was collected with an incident energy Ei = 150 meV. The fine-resolution Fermi chopper operated at a frequency of 600 Hz and the t0 chopper was spun at 90 Hz. Data normalisation with a vanadium standard ensured that differences in detector efficiencies and solid angle coverage were properly accounted for. The INS intensity from this experiment is plotted as \(\frac{{k}_{{\rm{i}}}}{{k}_{{\rm{f}}}}\,\)\(\frac{{\partial }^{2}\sigma }{\partial {{\Omega }}\partial E}\), where ki and kf are the incident and final neutron momenta respectively, Q is the momentum transfer, E is the energy transfer, and \(\frac{{\partial }^{2}\sigma }{\partial {{\Omega }}\partial E}\) is the double differential cross-section74. This quantity is proportional to the powder-averaged dynamical structure factor S(Q, E).
The absence of magnetic order in zero field down to 70 mK was confirmed with the fixed incident energy triple-axis spectrometer HB-1A of the High Flux Isotope Reactor (HFIR) at ORNL (λ = 2.37 Å). Yb2GaSbO7 powder was loaded in a Cu can and elastic scattering was measured both at 70 mK and 800 mK at Q values corresponding to the k = 0 Bragg positions. An excellent signal-to-noise ratio was achieved by generating an incident neutron beam with a double-bounce monochromator system and placing a pyrolytic graphite (PG) crystal analyser for energy discrimination before the single He-3 detector. The incident beam also had extremely low higher-order wavelength contamination due to the use of two PG filters. An energy resolution at the elastic line just over 1 meV (full-width half-maximum) was obtained by a using a collimation configuration of 40\(^{\prime}\)-40\(^{\prime}\)-40\(^{\prime}\)-80\(^{\prime}\).
Neutron powder diffraction (NPD) was performed on the high-resolution powder diffractometer HB-2A75 of HFIR at ORNL to investigate the evolution of the magnetic ground state for Yb2GaSbO7 in applied magnetic fields up to 4 T and temperatures down to 1.2 K. Pressed powder of Yb2GaSbO7 was loaded in a cylindrical Cu can, and the data were collected with a neutron wavelength of 2.41 Å and a collimation of open-21\(^{\prime}\)-12\(^{\prime}\). Rietveld refinements were performed using the FULLPROF software suite76 and the magnetic structure symmetry analysis was performed using SARAh77.
Additional neutron diffraction data were collected on the wide-angle neutron diffractometer WAND (λ = 1.48 Å) at the HFIR. Yb2GaSbO7 powder was loaded in a cylindrical Cu can and data was collected at temperatures between 1.5 and 10 K, with applied magnetic fields between 0 and 4.5 T. Contributions to the phase diagram (Fig. 5) from the WAND data were determined by measuring the temperature dependence of the (113) Bragg peak intensity at fixed applied magnetic fields.
The low-energy magnetic fluctuations of Yb2GaSbO7 were measured on the Disk Chopper Time-of-Flight Spectrometer DCS78 at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR). Yb2GaSbO7 powder was loaded in a cylindrical Cu can and then placed in an ICE dilution fridge insert of a cryostat. An incident wavelength λ = 4.8 Å in low-resolution mode was chosen, corresponding to a flux of ~ \(1\times10^6\) neutrons/s with an elastic line resolution of approximately 0.125 meV (full-width half-maximum) and an accessible Q range of [0.11, 2.45] Å−1 in the elastic channel.
Polarised diffuse neutron scattering experiments were performed on the Diffuse Scattering Spectrometer D779 at the Institut Laue-Langevin (ILL). An incident wavelength λ = 4.8 Å was selected by a double-focusing pyrolytic graphite monochromator. Data were collected in non-time-of-flight mode, leading to the extraction of the integrated scattering intensity with energy transfers up to an Ei = 3.5 meV. Yb2GaSbO7 powder was loaded in a double-wall cylindrical Cu can and then placed in the dilution fridge insert of a cryostat. Data normalisation by a vanadium standard ensured that differences in detector efficiency and solid angle coverage were taken into account. Scattering contributions from an empty and a cadmium-filled sample holder were added together and weighted by the sample transmission to estimate the instrument background. Corrections for polarisation efficiency of the supermirror analysers were made by using the scattering from amorphous quartz. Equal counting times were spent on measuring the scattering along the x, y, and z directions. The 6 pt. xyz-polarisation analysis method53 was used to separate scattering contributions from the magnetic, nuclear coherent, and nuclear spin incoherent scattering at different momentum transfers Q. The non-spin-flip and spin-flip scattering along each of the three directions were measured with a time ratio of 1:4.
Data availability
Raw bulk characterisation data were generated at the University of Winnipeg, the University of British Columbia, the University of Edinburgh, and the National High Magnetic Field Laboratory. Raw neutron scattering data were generated at the SNS (SEQUOIA), HFIR (HB-1A, HB-2A, and WAND), NIST (DCS), and the ILL (D7). Data included in this study are available from the corresponding authors upon reasonable request.
References
Ross, K. A., Savary, L., Gaulin, B. D. & Balents, L. Quantum excitations in quantum spin ice. Phys. Rev. X 1, 021002 (2011).
Gingras, M. J. P. & McClarty, P. A. Quantum spin ice: a search for gapless quantum spin liquids in pyrochlore magnets. Rep. Prog. Phys. 77, 056501 (2014).
D’Ortenzio, R. M. et al. Unconventional magnetic ground state in Yb2 Ti2 O7. Phys. Rev. B 88, 134428 (2013).
Hallas, A. M. et al. Universal dynamic magnetism in Yb pyrochlores with disparate ground states. Phys. Rev. B 93, 100403 (2016).
Zhu, Z., Maksimov, P. A., White, S. R. & Chernyshev, A. L. Disorder-induced mimicry of a spin liquid in YbMgGaO4. Phys. Rev. Lett. 119, 157201 (2017).
Li, Y. et al. Rare-earth triangular lattice spin liquid: A single-crystal study of YbMgGaO4. Phys. Rev. Lett. 115, 167203 (2015).
Miiller, W. et al. Magnetic structure of Yb2 Pt2 Pb: Ising moments on the Shastry-Sutherland lattice. Phys. Rev. B 93, 104419 (2016).
Shen, Y. et al. Evidence for a spinon Fermi surface in a triangular-lattice quantum-spin-liquid candidate. Nature 540, 559–562 (2016).
Wu, L. S. et al. Orbital-exchange and fractional quantum number excitations in an f-electron metal, Yb2 Pt2 Pb. Science 352, 1206–1210 (2016).
Baenitz, M. et al. NaYbS2: A planar spin-\(\frac{1}{2}\) triangular-lattice magnet and putative spin liquid. Phys. Rev. B 98, 220409 (2018).
Liu, W. et al. Rare-earth chalcogenides: A large family of triangular lattice spin liquid candidates. Chin. Phys. Lett. 35, 117501 (2018).
Zhang, X. et al. Hierarchy of exchange interactions in the triangular-lattice spin liquid YbMgGaO4. Phys. Rev. X 8, 031001 (2018).
Gannon, W. J. et al. Spinon confinement and a sharp longitudinal mode in Yb2 Pt2 Pb in magnetic fields. Nat. Commun. 10, 1123 (2019).
Xing, J. et al. Field-induced magnetic transition and spin fluctuations in the quantum spin-liquid candidate CsYbSe2. Phys. Rev. B 100, 220407 (2019).
Hallas, A. M., Gaudet, J. & Gaulin, B. D. Experimental insights into ground-state selection of quantum XY pyrochlores. Annu. Rev. Condens. Matter Phys. 9, 105–124 (2018).
Gaudet, J. et al. Neutron spectroscopic study of crystalline electric field excitations in stoichiometric and lightly stuffed Yb2Ti2O7. Phys. Rev. B 92, 134420 (2015).
Hallas, A. M. et al. XY antiferromagnetic ground state in the effective \(S=\frac{1}{2}\) pyrochlore Yb2Ge2O7. Phys. Rev. B 93, 104405 (2016).
Gao, B. et al. Experimental signatures of a three-dimensional quantum spin liquid in effective spin-1/2 Ce2 Zr2 O7 pyrochlore. Nat. Phys. 15, 1052–1057 (2019).
Gaudet, J. et al. Quantum spin ice dynamics in the dipole-octupole magnet Ce2 Zr2 O7. Phys. Rev. Lett. 122, 187201 (2019).
Sibille, R. et al. A quantum liquid of magnetic octupoles on the pyrochlore lattice. Nat. Phys. 16, 546–552 (2020).
Zouari, S., Ballou, R., Cheikh-Rouhou, A. & Strobel, P. Synthesis and structure of new pyrochlore-type oxides Ln2 ScNbO7 (Ln=Pr, Nd, Eu, Gd, Dy). Mater. Lett. 62, 3767–3769 (2008).
Strobel, P. et al. Structural and magnetic properties of new rare-earth - antimony pyrochlore-type oxides Ln2 BSbO7 (B=Sc, Ga, In). Solid State Sci. 12, 570–577 (2010).
Garcia Casado, P. & Rasines, I. The new pyrochlore Gd2GaSbO7. J. Phys. Chem. Solids 45, 447–448 (1984).
Garcia Casado, P., Mendiola, A. & Rasines, I. Preparation and crystallographic data of the pyrochlores Gd2 MSbO7 (M=Cr, Mn, Fe, In). J. Phys. Chem. Solids 46, 921–923 (1985).
Faurie, J. P., Boulon, G. & Delaigue, M. C. Elaboration et etude structurale des antimoniates de terres rares Ln2 Ln’SbO7 (Ln, Ln’=Lu, Y, Gd, ou Ga) a l’aide de la sonde ponctuelle Eu3+. J. Solid State Chem. 17, 7–14 (1976).
Ross, K. A. et al. Single-ion properties of the \({\text S}_{\text {eff}}=\frac{1}{2}\) XY antiferromagnetic pyrochlores NaA'Co2F7 (A' = Ca2+, Sr2+). Phys. Rev. B 95, 144414 (2017).
Gaulin, B. D. et al. Quenched crystal-field disorder and magnetic liquid ground states in Tb2 Sn2−x Tix O7. Phys. Rev. B 91, 245141 (2015).
Sarte, P. M. et al. Evidence for the confinement of magnetic monopoles in quantum spin ice. J. Phys.: Condens. Matter 29, 45LT01 (2017).
Shirai, M. et al. Doping-induced quantum crossover in Er2 Ti2−x Snx O7. Phys. Rev. B 96, 180411 (2017).
Ke, X. et al. Spin-ice behavior in Dy2 Sn2−x Sbx O7+x/2 and Dy2 NbScO7. Phys. Rev. B 76, 214413 (2007).
Hodges, J. A. et al. Magnetic frustration in the disordered pyrochlore Yb2 GaSbO7. J. Phys.: Condens. Matter 23, 164217 (2011).
Thompson, J. D. et al. Quasiparticle breakdown and spin Hamiltonian of the frustrated quantum pyrochlore Yb2 Ti2 O7 in a magnetic field. Phys. Rev. Lett. 119, 057203 (2017).
Kobayashi, Y., Miyashita, T., Fukamachi, T. & Sato, M. NMR studies of Ga in magnetically frustrated pyrochlore system R2 GaSbO7 (R = rare earth elements). J. Phys. Chem. Solids 62, 347–350 (2001).
Yasui, Y. et al. Ferromagnetic transition of pyrochlore compound Yb2 Ti2 O7. J. Phys. Soc. Jpn. 72, 3014–3015 (2003).
Chang, L. J. et al. Higgs transition from a magnetic Coulomb liquid to a ferromagnet in Yb2 Ti2 O7. Nat. Commun. 3, 992 (2012).
Gaudet, J. et al. Gapless quantum excitations from an icelike splayed ferromagnetic ground state in stoichiometric Yb2 Ti2 O7. Phys. Rev. B 93, 064406 (2016).
Yaouanc, A., Dalmas de Réotier, P., Keller, L., Roessli, B. & Forget, A. A novel type of splayed ferromagnetic order observed in Yb2 Ti2 O7. J. Phys.: Condens. Matter 28, 426002 (2016).
Arpino, K. E., Trump, B. A., Scheie, A. O., McQueen, T. M. & Koohpayeh, S. M. Impact of stoichiometry of Yb2Ti2O7 on its physical properties. Phys. Rev. B 95, 094407 (2017).
Scheie, A. et al. Multiphase magnetism in Yb2Ti2O7. PNAS 117, 27245 (2020).
Hodges, J. A. et al. The crystal field and exchange interactions in Yb2Ti2O7. J. Phys.: Condens. Matter 13, 9301–9310 (2001).
Yan, H., Benton, O., Jaubert, L. & Shannon, N. Theory of multiple-phase competition in pyrochlore magnets with anisotropic exchange with application to Yb2Ti2O7, Er2Ti2O7, and Er2Sn2O7. Phys. Rev. B 95, 094422 (2017).
Bertin, A., Chapuis, Y., Dalmas de Réotier, P. & Yaouanc, A. Crystal electric field in the R2Ti2O7 pyrochlore compounds. J. Phys.: Condens. Matter 24, 256003 (2012).
Sato, T. & Miyako, Y. Nonlinear susceptibility and specific heat of (Pd0.9966 Fe0.0034)0.95 Mn0.05. J. Phys. Soc. Jpn. 51, 1394–1400 (1982).
Dun, Z. L. et al. Chemical pressure effects on magnetism in the quantum spin liquid candidates Yb2X2 O7 (X = Sn, Ti, Ge). Phys. Rev. B 89, 064401 (2014).
Steppke, A. et al. Nuclear contribution to the specific heat of Yb(Rh0.93 Co0.07)2 Si2. Phys. Status Solidi B 247, 737–739 (2010).
Dun, Z. L. et al. Antiferromagnetic order in the pyrochlores R2Ge2O7 (R = Er, Yb). Phys. Rev. B 92, 140407 (2015).
Hodges, J. A. et al. First-order transition in the spin dynamics of geometrically frustrated Yb2Ti2O7. Phys. Rev. Lett. 88, 077204 (2002).
Cai, Y. Q. et al. High-pressure synthesis and characterization of the effective pseudospin S = 1/2 XY pyrochlores R2Pt2O7 (R = Er, Yb). Phys. Rev. B 93, 014443 (2016).
Dun, Z. L. et al. Yb2 Sn2 O7: A magnetic Coulomb liquid at a quantum critical point. Phys. Rev. B 87, 134408 (2013).
Yaouanc, A. et al. Dynamical splayed ferromagnetic ground state in the quantum spin ice Yb2Sn2O7. Phys. Rev. Lett. 110, 127207 (2013).
Hallas, A. M. et al. Phase competition in the Palmer-Chalker XY pyrochlore Er2Pt2O7. Phys. Rev. Lett. 119, 187201 (2017).
Lago, J. et al. Glassy dynamics in the low-temperature inhomogeneous ferromagnetic phase of the quantum spin ice Yb2 Sn2 O7. Phys. Rev. B 89, 024421 (2014).
Schärpf, O. & Capellmann, H. The XYZ-difference method with polarized neutrons and the separation of coherent, spin incoherent, and magnetic scattering cross sections in a multidetector. Phys. Status Solidi A 135, 359–379 (1993).
Sarte, P. M. et al. Ordered magnetism in the intrinsically decorated \(j_{\rm{eff}}=\frac{1}{2} \, \alpha-{\rm{CoV}}_3{\rm{O}}_8\). Phys. Rev. B 98, 224410 (2018).
Ross, K. A., Krizan, J. W., Rodriguez-Rivera, J. A., Cava, R. J. & Broholm, C. L. Static and dynamic XY-like short-range order in a frustrated magnet with exchange disorder. Phys. Rev. B 93, 014433 (2016).
Plumb, K. W. et al. Continuum of quantum fluctuations in three-dimensional S = 1 Heisenberg magnet. Nat. Phys. 15, 54–59 (2019).
Paddison, J. A. M. & Goodwin, A. L. Empirical magnetic structure solution of frustrated spin systems. Phys. Rev. Lett. 108, 017204 (2012).
Paddison, J. A. M., Stewart, J. R. & Goodwin, A. L. SPINVERT: a program for refinement of paramagnetic diffuse scattering data. J. Phys.: Condens. Matter 25, 454220 (2013).
Moessner, R. & Chalker, J. T. Low-temperature properties of classical geometrically frustrated antiferromagnets. Phys. Rev. B 58, 12049–12062 (1998).
Lamsal, J. & Montfrooij, W. Extracting paramagnon excitations from resonant inelastic x-ray scattering experiments. Phys. Rev. B 93, 214513 (2016).
Guedel, H. U., Stebler, A. & Furrer, A. Direct observation of singlet-triplet separation in dimeric copper (II) acetate by neutron inelastic scattering spectroscopy. Inorg. Chem. 18, 1021–1023 (1979).
Uematsu, K. & Kawamura, H. Randomness-induced quantum spin liquid behavior in the s = 1/2 random-bond Heisenberg antiferromagnet on the pyrochlore lattice. Phys. Rev. Lett. 123, 087201 (2019).
Kimchi, I., Sheckelton, J. P., McQueen, T. M. & Lee, P. A. Scaling and data collapse from local moments in frustrated disordered quantum spin systems. Nat. Commun. 9, 4367 (2018).
Ross, K. A. et al. Two-dimensional Kagome correlations and field induced order in the ferromagnetic XY pyrochlore Yb2Ti2O7. Phys. Rev. Lett. 103, 227202 (2009).
Ross, K. A. et al. Lightly stuffed pyrochlore structure of single-crystalline Yb2 Ti2 O7 grown by the optical floating zone technique. Phys. Rev. B 86, 174424 (2012).
Takahashi, S. K. et al. Low-frequency spin dynamics in the XY quantum spin ice Yb2Pt2O7. Phys. Rev. B 98, 104425 (2018).
Li, Y. et al. Crystalline electric-field randomness in the triangular lattice spin-liquid YbMgGaO4. Phys. Rev. Lett. 118, 107202 (2017).
Ma, Z. et al. Spin-glass ground state in a triangular-lattice compound YbZnGaO4. Phys. Rev. Lett. 120, 087201 (2018).
Li, Y. et al. Muon spin relaxation evidence for the U(1) quantum spin-liquid ground state in the triangular antiferromagnet YbMgGaO4. Phys. Rev. Lett. 117, 097201 (2016).
Paddison, J. A. M. et al. Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4. Nat. Phys. 13, 117–122 (2017).
Li, Y. et al. Rearrangement of uncorrelated valence bonds evidenced by low-energy spin excitations in YbMgGaO4. Phys. Rev. Lett. 122, 137201 (2019).
Blӧte, H. W. J., Wielinga, R. F. & Huiskamp, W. J. Heat-capacity measurements on rare-earth double oxides R2M2O7. Physica 43, 549–568 (1969).
Granroth, G. E. et al. SEQUOIA: A newly operating chopper spectrometer at the SNS. J. Phys.: Conf. Ser. 251, 012058 (2010).
Squires, G. L. Introduction to the Theory of Thermal Neutron Scattering (Cambridge University Press, 2012).
Calder, S. et al. A suite-level review of the neutron powder diffraction instruments at Oak Ridge National Laboratory. Rev. Sci. Instrum. 89, 092701 (2018).
Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 192, 55–69 (1993).
Wills, A. S. A new protocol for the determination of magnetic structures using simulated annealing and representational analysis (SARAh). Phys. B 276, 680–681 (2000).
Copley, J. R. D. & Cook, J. C. The Disk Chopper Spectrometer at NIST: a new instrument for quasielastic neutron scattering studies. Chem. Phys. 292, 477–485 (2003).
Stewart, J. R. et al. Disordered materials studied using neutron polarization analysis on the multi-detector spectrometer. D7. J. Appl. Crystallogr. 42, 69–84 (2009).
Acknowledgements
We acknowledge useful conversations with A.J. Browne, G.M. McNally, G. Perversi, T.J. Williams, K.J. Camacho, R.K. Camacho, A. Reyes, and C. Schwenk. P.M.S. & B.R.O. acknowledge financial support from the University of California, Santa Barbara through the Elings Fellowship. P.M.S. acknowledges additional financial support from the CCSF, RSC, ERC, and the University of Edinburgh through the GRS and PCDS. C.R.W. acknowledges financial support from the CRC (Tier II) programme, the Leverhulme Trust, CIFAR, CFI and NSERC. M.M.B. acknowledges partial support by the National Science Foundation Graduate Research Fellowship Programme under Grant No. 1650114. S.D.W. and M.M.B. acknowledge financial support from the US Department of Energy (DOE), Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Grant No. DE-SC0017752. H.D.Z. acknowledges financial support from Grant No. NSF-DMR-2003117. This material is based upon work supported by the National Science Foundation’s Q-AMASE-i initiative under award DMR-1906325. J.A.M.P.’s work was supported by the Laboratory Directed Research and Development Programme of Oak Ridge National Laboratory, managed by UT-Battelle, LLC for the US Department of Energy. The authors would like to thank the Carnegie Trust for the Universities of Scotland for providing facilities and equipment for chemical synthesis. This research was undertaken thanks in part to funding from the Max Planck-UBC-UTokyo Centre for Quantum Materials and the Canada First Research Excellence Fund, Quantum Materials and Future Technologies Programme. A portion of this work was performed at the NHMFL, which is supported by National Science Foundation Cooperative Agreement No. DMR-1157490 and the State of Florida. Access to DCS was provided by the Center for High-Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under Agreement No. DMR-2010792. A portion of this research used resources at the Spallation Neutron Source and High Flux Isotope Reactor, which are DOE Office of Science User Facilities operated by Oak Ridge National Laboratory. Neutron data collection (https://doi.org/10.5291/ILL-DATA.5-32-849) on the Diffuse Scattering Spectrometer D7 at the ILL took place with financial support from proposal 5-32-849 awarded to P.M.S., J.P.A., L.M., and C.R.W.
Author information
Authors and Affiliations
Contributions
P.M.S., J.A.M.P., A.A.A., and C.R.W. conceived the study and wrote the manuscript with contributions and comments from all authors. P.M.S. and H.D.Z. synthesised polycrystalline samples of Yb2GaSbO7 and verified phase purity with x-ray diffraction. P.M.S., K.C., D.R.-i.-P., M.L., E.S.C., H.D.Z., A.M.H., A.A.A., and C.R.W. collected and analysed the bulk characterisation data. P.M.S., B.R.O., K.H.H., M.M.B., C.S., H.D.Z., J.A.M.P., A.A.A., and C.R.W. collected and analysed the neutron scattering data. J.P.A. and S.D.W. provided support and guidance to some of the junior members working on this project. M.B.S., S.C., D.M.P., L.M., and Y.Q. provided support and expertise at the beamlines during the neutron scattering experiments.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sarte, P.M., Cruz-Kan, K., Ortiz, B.R. et al. Dynamical ground state in the XY pyrochlore Yb2GaSbO7. npj Quantum Mater. 6, 42 (2021). https://doi.org/10.1038/s41535-021-00343-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00343-4