Abstract
Nonreciprocal directional dichroism is an unusual light–matter interaction that gives rise to diode-like behavior in low-symmetry materials. The chiral varieties are particularly scarce due to the requirements for strong spin–orbit coupling, broken time-reversal symmetry, and a chiral axis. Here we bring together magneto-optical spectroscopy and first-principles calculations to reveal high-energy, broadband nonreciprocal directional dichroism in Ni3TeO6 with special focus on behavior in the metamagnetic phase above 52 T. In addition to demonstrating this effect in the magnetochiral configuration, we explore the transverse magnetochiral orientation in which applied field and light propagation are orthogonal to the chiral axis and, by so doing, uncover an additional configuration with a unique nonreciprocal response in the visible part of the spectrum. In a significant conceptual advance, we use first-principles methods to analyze how the Ni2+ d-to-d on-site excitations develop magneto-electric character and present a microscopic model that unlocks the door to theory-driven discovery of chiral magnets with nonreciprocal properties.
Similar content being viewed by others
Introduction
Strong spin–orbit coupling and broken symmetries give rise to many novel properties in materials. One of the more peculiar is nonreciprocal directional dichroism or “one-way transparency”1,2. A nonreciprocal effect occurs when the motion of an object in one direction is different from that in the opposite direction3. Proof-of-concept examples include electrical transport in chiral WS2 and carbon nanotubes4,5 and layered CrNb3S66, spin wave nonreciprocity in magnetic TaPy bilayers7 and antiferromagnetic Ba3NbFe3Si2O148, and propagation of sound velocity and excitations along skyrmion strings in chiral Cu2OSeO39,10. Spectroscopically, the effect occurs in the vicinity of a magnetoelectric excitation and arises from how absorption depends on the light propagation direction1,3,11. Thus, a given sample may be highly transmitting when measured with light propagating in the +k direction, but strongly absorbing for light in the −k direction.
There are stringent symmetry requirements for a nonreciprocal effect to occur. For a given propagation direction \(\hat{k}\), all symmetries that would reverse k to −k must be broken, including inversion, mirrors or C2 rotations about a plane or axis perpendicular to \(\hat{k}\), and time reversal3,11. As one might anticipate, this is relatively rare. There are several different measurement configurations that can be used to take advantage of various types of symmetry breaking3. Toroidal dichroism is the most well-studied case12,13,14. It occurs when light propagation is along the toroidal moment T, (k ∥ T = P × M, where P and M are the electric polarization and magnetic moment of the material, respectively). A second, less common mechanism takes place in chiral magnets15,16,17,18,19,20,21,22,23. Here, light is directed along the chiral axis and the external magnetic field direction. This nonreciprocal effect is called magnetochiral dichroism. Each chiral domain of the crystal has two eigenstates that can be independently addressed with linearly or circularly polarized light24. Although it is often anticipated that linearly or circularly polarized light must be used to observe a nonreciprocal behavior, unpolarized light can also reveal the effect17,25. In fact, the beauty of magnetochiral materials such as Ni3TeO6 is that nonreciprocal directional dichroism can be observed with unpolarized light. The realization of polarization-independent nonreciprocal behavior in single-phase materials can be extremely useful for optical isolators and rectifiers in photonic integrated circuits and high-fidelity holograms26,27,28.
As nonreciprocal directional dichroism depends upon both the electric and magnetic-dipole matrix elements1, magnetoelectric multiferroics—with their low crystallographic and magnetic symmetries—are promising platforms with which to search for these effects. Most materials identified so far have been studied in the terahertz region to reveal nonreciprocity in the vicinity of the electromagnon. Examples include BiFeO329,30, CaBaCo4O713, FeZnMo3O824,25, Ba2CoGe2O712,15, and (Eu,Y)MnO331. An electromagnon has natural magnetoelectric character and the energy scale of the light and that of the spins is similar. There are also examples of broadband nonreciprocal directional dichroism at higher energies—for instance, in GaFeO332,33 and CuB2O416,17,28,33,34,35. In many of the aforementioned cases, the authors reversed the direction of the external magnetic field rather than the light propagation direction. This approach has clear experimental advantages and is valid for materials with a switchable magnetic moment. Whether the effect is actually symmetric (or not) with respect to switching H or k is highly underexplored.
Ni3TeO6 provides a platform with which to test these ideas of nonreciprocity. The material shows one of the largest magnetoelectric coupling constants known to date36,37. The crystal structure is corundum-like with an R3 space group38. Each Ni and Te ion is surrounded by six oxygen centers—all of which are inequivalent38. In addition to a Ni1, Ni2, Ni3, Te alignment along c, the R3 space group supports a c-directed chiral axis39. The magnetic field–temperature (H–T) phase diagram in Fig. 1a summarizes the important energy scales36,37. Below TN = 53 K, the Ni spins align to form a collinear antiferromagnet. Electric polarization grows substantially below TN. Under magnetic field (H ∥ c), there is a 9 T spin flop (SF) and a 52 T transition to the metamagnetic (MM) phase. Polarization can be controlled across both of these magnetically driven transitions36,37. The optical absorption of Ni3TeO6 is summarized in Fig. 1b. The features between 0.7 and 2.6 eV, spanning the near-infrared and visible regions, are assigned as Ni d-to-d on-site excitations. The anisotropy is a consequence of the crystal structure40. In a mono-axial chiral material such as Ni3TeO6, the direction of the chiral axis and the pitch of the chiral rotation39 are well-defined, and impact the magneto-optical response. There are two orientations of interest41. In Fig. 1c the chiral axis is normal to ab-plane polished crystal, whereas in Fig. 1f the chiral axis is in-plane. These crystal settings enable spectroscopic measurements in the magnetochiral and transverse magnetochiral orientations, respectively (Fig. 1c, f). Both are in the Faraday geometry (k ∥ H) as shown in the schematics, but the direction of applied field and light propagation are different with respect to the chiral axis. Although the magnetochiral orientation has been demonstrated in a handful of cases3,15,17, the transverse magnetochiral orientation is completely unexplored—although it clearly breaks the requisite symmetries (Supplementary Information)41. Ni3TeO6 is relatively unique in that both the magnetochiral and transverse magnetochiral results can be explored in the same system.
a Comprehensive H–T phase diagram for H ∥ c36,37,40. AFM, antiferromagnet; SF, spin flop, MM, metamagnetic. The phase diagram in the transverse configuration exhibits only gradual canting with increasing field37. b Optical absorption spectrum of Ni3TeO6. The on-site Ni d-to-d excitations are labeled40. c Schematic representation of magnetochiral dichroism. This measurement orientation requires a chiral axis in the material as well as light (±k) and magnetic field ±H aligned along the chiral direction in the Faraday geometry. The nonreciprocal effect will depend upon light propagation and field direction. The symmetry considerations are fully discussed in the Supplementary Information. d Image of the ab-plane sample under crossed linear polarizer and analyzer. The red circle indicates the position of the light spot, which is within a single chiral domain. e Optical rotation measurement using crossed polarizer and analyzer. The angle Θ corresponds to the angle between the analyzer and normal from the polarizer. The red symbols correspond to the lighter green portion of the crystal and the blue symbols correspond to the darker green portion in the corners. f The nonreciprocal effect also occurs in the transverse magnetochiral orientation. Here we maintain the Faraday geometry (with ±k and ±H) but the chiral (c) axis is in the plane of the polished crystal. The symmetry considerations of this unique geometry are discussed in the Supplementary Information. g Photographic image in which the c-axis is in the plane of the polished crystal under crossed linear polarizer and analyzer. The red circle indicates the measurement region, which is within a single chiral domain.
Results and discussion
Nonreciprocal effects in Ni3TeO6
As indicated earlier, Ni3TeO6 has several different magnetic phases accessible under external field when H ∥ c (Fig. 1a). Except in the zero-field antiferromagnetic ground state, the symmetry conditions for the existence of non-reciprocal directional dichroism are satisfied, but one may wonder whether the effect is large enough to be detectable in the visible frequency range. Here, the absorption is dominated by Ni2+ d-to-d on-site excitations. These are known to be magnetoelectric, not only because the excitations are sensitive to the microscopic spin arrangement in each magnetic phase40 but also due to spin–orbit coupling, which becomes significant in the excited state.
As we shall see later, our first-principles-based theory not only estimates the d-to-d electric and magnetic-dipole excitations, but also indicates that spin–orbit coupling is a critical element in the nonreciprocal directional dichroism. Specifically, the nonreciprocal component of the absorption for light propagating along the z-direction is found to be1,42
where N±(ω) is the complex refractive index for light propagating along the ±z-direction with frequency ω, and \({\chi }_{yx}^{{\rm{me}}}(\omega )\) and \({\chi }_{xy}^{{\rm{em}}}(\omega )\) are the off-diagonal components of the dimensionless magneto-electric and electro-magnetic response tensors. See Eq. (2) or the Methods section for their explicit linear-response form. It will be shown in the following section that, without spin–orbit coupling, the \({\chi }_{yx}^{{\rm{me}}}\) and \({\chi }_{xy}^{{\rm{em}}}\) responses cancel each other, so that there is no k-direction-dependent component even in the presence of magnetism. Our first-principles calculations, presented later suggest that a nonreciprocal directional dichroism signal on the order of one part in 102 should be observable for the Ni d-to-d excitations even with a relatively weak (≈30 meV) spin–orbit coupling within the Ni d shell. Hence, Ni3TeO6 is a good candidate with which to explore nonreciprocal directional dichroism in the vicinity of d-to-d excitations in the visible range, where such effects have rarely been discussed.
With these ideas in mind, we polished two different single crystals (Fig. 1d, g). Evidence for a single domain character39—at least in the measurement area—is evident in these images, the optical rotation data (Fig. 1e), and elaborated in the Supplementary Information.
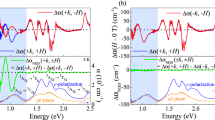
Figure 2 summarizes nonreciprocal directional dichroism in Ni3TeO6. The measurements were performed in transmission and the spectra are obtained after removing the zero-field spectrum, i.e., Δα(H) = α(H) − α(H = 0), or by subtracting these absorption difference curves to get the nonreciprocal response. Focusing first on the magnetochiral orientation (Fig. 2a–f), we find a large nonreciprocal response in the vicinity of the on-site d-to-d excitations. Reversing the direction of magnetic field H while keeping k constant yields absorption difference curves (Δα) that are distinct in several respects (Fig. 2b). To find the nonreciprocal response, we subtract the two Δα curves: ΔαNDD = Δα+H − Δα−H (Fig. 2c). This difference corresponds to the absorption of light in one field direction vs. that in the other field direction. To further test the nonreciprocal effect, we held H constant, while reversing the light propagation direction k (Fig. 2d–f). The absorption difference spectra and ΔαNDD are virtually identical to the data obtained by switching the direction of the applied field under constant k. Thus, in addition to revealing broadband nonreciprocal directional dichroism at much higher energies than usual in Ni3TeO6, the effect is also reasonably large. The overall magnitude of the effect ranges up to 35% depending upon the energy. We elaborate on the size of the nonreciprocal effect in Ni3TeO6 and compare the results with other materials in the Supplementary Information.
All of this work was done with unpolarized light, which has a number of advantages for applications. As a point of comparison, magnetochiral dichroism in the optical region has also been realized in CuB2O4—both with and without polarized light17. In that work, ΔαNDD arises from the mixing of electronic- and magnetic-dipole transitions due to spin–orbit coupling, which in turn activates the intra-atomic d-to-d Cu2+ transitions17. On-site Fe2+ excitations also support giant photoinduced Kerr rotations in (Fe1−xZnx)Mo3O824. In this case, the fundamental eigenmodes are addressed with circularly polarized light, but the broadband aspect is neglected. We anticipate that circular or linear polarizers would amplify the size of non-reciprocal effects in Ni3TeO6. Circular polarizers generally cover a very limited spectral range, so it is challenging in practice to explore broadband effects.
a, d Schematic view of H and k relative to the chiral axis of Ni3TeO6 in the magnetochiral orientation. b Magneto-optical response as measured by the absorption difference at full field, Δα = α(H = ±62 T) − α(H = 0 T). Data in the +H direction are different than those in the −H direction. c Nonreciprocal directional dichroism of Ni3TeO6 in the metamagnetic phase in the magnetochiral orientation, obtained by reversing the field direction with fixed k. Thus, ΔαNDD = α+H(62 T) − α−H(−62 T), which is the same as Δα+H(62 T) − Δα−H(−62 T). For reference in c, f we include the linear absorption spectrum α. e, f Similar Δα and ΔαNDD spectra are obtained by reversing the light propagation direction under constant field. Here, Δα is α(H = +62 T) − α(H = 0 T) for up/down k, and ΔαNDD is αupk − αdownk, which is the same as Δαupk − Δαdownk with H = +62 T. g, j Schematic view of H and k relative to the chiral axis of Ni3TeO6 in the transverse magnetochiral orientation. h, i Magneto-optical and nonreciprocal directional dichroism of Ni3TeO6 at 62 T in the transverse magnetochiral orientation obtained by reversing the field direction under constant k. For reference in i, l, we include the linear absorption spectrum. k, l Similar Δα and ΔαNDD spectra are obtained by reversing the light propagation direction under constant field.
We also reached beyond the magnetochiral orientation to explore nonreciprocal directional dichroism in other settings. Our objectives are to (i) seek out strange new types of light–matter interactions in chiral magnets and (ii) to compare their character with the more established variants. Figure 1f, g summarizes the sample requirements (exposing the mono-chiral c-axis in the plane of the polished single domain crystal) and Faraday measurement geometry for uncovering the nonreciprocal directional dichroism in the transverse magnetochiral orientation41. The lower portion of Fig. 2 summarizes our spectroscopic results. As before, we switch both allowed parameters. We reversed the applied field direction while keeping the light propagation fixed (Fig. 2g–i) and we reversed k under constant H (Fig. 2j, l). Clearly, nonreciprocal directional dichroism in the transverse magnetochiral orientation differs greatly from that in the magnetochiral orientation. Not only is ΔαNDD overall broader, encompassing two active spectral regimes across the near-infrared and visible that are more than 0.5 eV wide, but it is also large—on the order of ±50 cm−1. More importantly, the transverse magnetochiral measurement configuration is unique within the current framework of magnetochiral dichroism3. In this configuration, nonreciprocal directional dichroism appears as soon as there is an overall magnetic moment—even below 1 T. Spectra up to 62 T simply demonstrate that the size of the effect increases with the overall magnetic moment and can be controlled by the field. These results were achieved with unpolarized light.
Microscopic model for nonreciprocal directional dichroims in chiral magnets
As shown in the previous literature1,2, nonreciprocal directional dichroism is a byproduct of magnetoelectric excitations, which in our case are the Ni2+ d-to-d excitations between atomic multiplet states in Ni3TeO6. The magnetoelectic coupling tensors \({\chi }_{\alpha \beta }^{{\rm{me}}}\) and \({\chi }_{\alpha \beta }^{{\rm{em}}}\) in the linear-response regime take the form43
where \({\kappa }_{0}=\sqrt{{\mu }_{0}/{\epsilon }_{0}}\), ωn0 ≡ ωn − ω0, and \({M}_{\alpha }^{n0}\equiv \left\langle n\right|{M}_{\alpha }\left|0\right\rangle\) and \({P}_{\beta }^{n0}\equiv \left\langle n\right|{P}_{\beta }\left|0\right\rangle\) are matrix elements in Cartesian directions α and β of magnetic (M) and electric (P) dipole operators, respectively, taken between ground (\(\left|0\right\rangle\)) and excited (\(\left|n\right\rangle\)) states, both within the d8 atomic multiplet configuration. The broadening δ originates from hybridizations between the Ni d shell and its environment of oxygen and other neighboring sites. Assuming the hybridization-induced broadening δ is small compared with the excitation energies ωn0 in the mid-gap energy range of this wide gap (≃2.7 eV) insulator, a calculation of \({\chi }_{\alpha \beta }^{{\rm{me}}}\) and \({\chi }_{\alpha \beta }^{{\rm{em}}}\) in an atomic-like limit is a plausible first-order approximation, which requires the knowledge of the crystal field splittings and spin–orbit coupling (both extracted from density functional theory (DFT) simulation) and Hund’s coupling strength (estimated to be JH = 0.8 eV).
The critical role of spin–orbit coupling in the nonreciprocal directional dichroism of Eq. (1) can be seen from its explicit form,
which has been obtained by plugging Eq. (2) into (1) and keeping only the absorption part (ω ≃ ωn0). When spin–orbit coupling is absent, one can choose all spatial eigenstates to be real, in which case \({M}_{y}^{n0}\) and \({P}_{x}^{0n}\) become purely real and imaginary, respectively, yielding \({\rm{Re}}[{M}_{y}^{0n}{P}_{x}^{n0}]=0\). Hence, it can be seen that the spin–orbit coupling is a critical component of the nonreciprocal effect, at least in the linear-response regime.
Figure 3 shows a summary of our calculations. We obtain the multiplet eigenstates by exactly diagonalizing the many-body Hamiltonian within the Ni d shell on each Ni site, where this Hamiltonian includes the crystal fields and the spin–orbit coupling estimated from the first-principles density functional calculations, in addition to local exchange fields to incorporate magnetic order. The dipole matrix elements P0n and M0n are also extracted from the first-principles simulation and properly projected onto the localized 3d multiplet states (see Methods section for further details). Comparing Fig. 3a and b, it can be seen not only that the simulation yields reasonable agreement for the ratio between the nonreciprocal and reciprocal parts of the absorption spectra, ∣ΔαNDD/α∣ ≃ 0.03, but also that it reproduces the features occurring around ω ~ 1 eV, which corresponds to the excitation energy from 3A2g to 3T2g states. It is noteworthy that the vanishing of ΔαNDD in the collinear antiferromagnetic phase and its gradual enhancement as a function of H-field is also well reproduced as shown in Fig. 3c43, where magnetic configurations at different strength of H (adopted from ref. 37) is illustrated in Fig. 3d. It is also worth noting that threefold symmetry should be retained in experimental magnetochiral setup due to the presence of three magnetic domains equivalent up to threefold rotations even in SF and MM phases. The agreement between theory and experiment becomes poorer near the band edge, where the itinerant character of electrons is more dominant.
a Simulated absorption spectra α and nonreciprocal responses ΔαNDD ≡ α(+H) − α(−H) for the magnetic phase at H = 66 T from ab-initio calculations. b Experimental data in the magnetochiral configuration is shown for comparison. c Nonreciprocal responses from different magnetic configurations (offset vertically for clarity). Note that in a–c, relative nonreciprocal response ΔαNDD/αmax is presented, where αmax is the maximum value of simulated or experimental absorption α(E) in the energy range of 0.5 < E < 2.5 eV. d Spin configurations under various magnetic fields applied along c (reproduced from ref. 37). Here, SF and MM denote spin-flop and metamagnetic phases, respectively.
Remarkably, the relatively small spin–orbit coupling (≲40 meV) gives rise to a nonreciprocal contribution up to 3% of the absorption spectra, implying even larger nonreciprocal signals may be realized in systems with stronger spin–orbit coupling. Interestingly, the weak spin–orbit coupling in Ni (about 30 meV within the t2g shell) is enhanced (30 → 40 meV) by the presence of Te via hybridization in this compound. This observation suggests the intriguing possibility of amplifying spin–orbit induced physics and nonreciprocal optical effects in compounds where magnetically active transition-metal atoms coexist with nonmagnetic heavy atoms in their immediate environment.
Testing the effects of switching H and k
We also sought to compare field reversal vs. light propagation effects on nonreciprocal directional dichroism in Ni3TeO6. Figure 4a, b presents ΔαNDD under varying H and k conditions for the magnetochiral and transverse magnetochiral measurement symmetries, respectively. As anticipated for a mono-chiral system with a switchable moment, the overall shape of ΔαNDD in Ni3TeO6 does not depend upon whether the magnetic field or light propagation direction is switched. The response in the magneto- and transverse magnetochiral orientations is, however, quite different. In particular, ΔαNDD in the transverse magnetochiral orientation includes a large contribution from the c-direction and, as a result, has an extra functional region (highlighted by the green band) that does not have a counterpart in the more traditional magnetochiral response. To provide additional insight into the variation of the nonreciprocal effect across the SF and MM transitions, we calculated the change in oscillator strength ΔfNDD and plotted the result as a function of applied field. For the magnetochiral orientation (Fig. 4d), ΔfNDD is initially zero. This is because there is no overall magnetic moment because spins are collinear along c37. A small moment develops at 9 T when the spins flop into the ab-plane. Above 9 T, the spins cant with increasing field, inducing large changes in ΔαNDD. The nonreciprocal response in the transverse magnetochiral orientation is different (Fig. 4e). Here, ΔfNDD increases gradually as the spins cant toward the field and the overall magnetic moment increases. As a reminder, the easy axis is along c and in-plane in this geometry (and perpendicular to the magnetic field). There are no hysteresis effects within our sensitivity.
a ΔαNDD under different field and light propagation directions in the magnetochiral orientation for Ni3TeO6. b ΔαNDD under different field and light propagation directions in the transverse magnetochiral orientation. c Linear absorption spectrum at 4.2 K for reference. d, e Changes in the nonreciprocal response of Ni3TeO6, as measured by the change in oscillator strength Δf, as a of function magnetic field for the magnetochiral and transverse magnetochiral orientations, respectively. Zero-field data, both before and after the field pulse, is shown. Insets display close-up views of ΔαNDD spectra as a function of magnetic field. f Schematic showing the symmetry in the two scenarios when both H and k are changed. g–j Comparison of Δα and ΔαNDD spectra when both H and k are switched in the magnetochiral (g, h) and transverse magnetochiral (i, j) orientations.
From the symmetry standpoint, the nonreciprocal effect arises from the reversal of H or k3,44. Further, when both H and k are switched, ΔαNDD should vanish, as the two scenarios shown in Fig. 4f are related by time-reversal symmetry. We can test this supposition in Ni3TeO6, as we performed both sets of experiments. Figure 4g-j summarizes the effect of switching both field and the direction of light propagation for the two measurement orientations of interest. Turning first to the transverse magnetochiral orientation case (Fig. 4i, j), we find that simultaneously switching both H and k reveals almost no residual nonreciprocal response. Thus, the system is symmetric to reversal of both H and k in this configuration—as one might expect. The partial sum rule is therefore obeyed20,44,45.
We also extracted ΔαNDD = Δα+H,upk − Δα−H,downk for Ni3TeO6 in the magnetochiral orientation (Fig. 4g, h). Here, there is a small residual response indicating an apparent asymmetry in the measured nonreciprocal directional dichroism. One may wonder whether this contrast might be attributed to additional symmetry breaking due to the presence of structural chirality and/or electric polarization, but symmetry arguments indicate otherwise. That is, application of time reversal to the image in the top panel of Fig. 4f produces the image in the bottom panel (without reversing chirality or polarization), so the light propagation properties must be identical. To put it another way, if one were to reverse only the polarization in the top panel, non-reciprocal directional dichroism would still be identical, as the two measurements are related by a twofold rotation of the experimental setup about an in-plane axis followed by time reversal. (This operation reverses P but not H, k, or chirality.) We are currently uncertain about the source of the discrepancies visible in Fig. 4g, h, but we note the polar nature of the crystal implies an inequivalence between the top and bottom crystal surfaces, and we speculate that differences in surface charge, reflectivity, roughness, adsorbed molecular species, or other properties of the surface could be responsible. We are unaware of other instances of such behavior—although studies in which both H and k are reverse are not very common.
To summarize, we combined pulsed field techniques, optical spectroscopy, and first-principles calculations to reveal high-energy, broadband nonreciprocal directional dichroism in Ni3TeO6. This unusual light–matter interaction is enabled by spin–orbit coupling, which gives magnetoelectric character to the on-site d-to-d excitations of Ni2+ and analysis of the symmetry requirements led to the discovery of nonreciprocal effects in both the magnetochiral and transverse magnetochiral orientations. In the latter, field begins to control the overall magnetic moment even at the smallest values, which, combined with the use of unpolarized light, opens the door to a number of applications including optical isolators, rectifiers, and high-fidelity holograms26,27,28. Moreover, tests in which we compare switching H vs. k give a moderately consistent response in the magnetochiral case and nearly exact agreement in the transverse magnetochiral orientation. In a significant conceptual advance, our newly developed first-principles formalism enables the quantitative study of dynamical multiferroics beyond a conventional symmetry analyses, pioneering a powerful new approach in the search for candidate functional materials. Insights from our theoretical work already suggest, for instance, that 3d/4d- or 3d/5d-containing magnets with sizable spin–orbit coupling will be exciting playgrounds for optical-diode effects. The ability to screen for these effects in advance of any measurement will accelerate the the design, discovery, and deterministic control of nonreciprocity in variety of quantum materials.
Methods
High-quality single crystals were grown using the chemical vapour transport method36 and polished in two different orientations to thicknesses between 28 and 50 μm, to control optical density. One orientation exposed the ab-plane whereas the other contained the c-axis in the plane of the polished surface (Fig. 1c, f). Evidence for single domain character of these samples is given in Fig. 1d, e, g and discussed in detail in the Supplementary Information. To reinforce our polished samples in pulsed fields, we coated them with a transparent epoxy. Optical transmittance was measured as a function of energy and temperature in the ab-plane and in the c-direction using a series of spectrometers (0.4–3.0 eV; 4.2–300 K)40. Absorption was calculated as \(\alpha (E)=-(1/d){\rm{ln}}({\mathcal{T}}(E))\), where \({\mathcal{T}}(E)\) is the transmittance and d is the sample thickness. For the oscillator strength analysis, \(\Delta {f}_{{\rm{NDD}}}=(2c)/({N}_{e}\pi {\omega }_{p}^{2})\mathop{\int}\nolimits_{{E}_{1}}^{{E}_{2}}n\Delta {\alpha }_{{\rm{NDD}}}(E)dE\), where Ne is the number of electrons per Ni site, n is the refractive index, ωp is the plasma frequency \({\omega }_{p}\equiv \sqrt{({e}^{2}\rho )/(m{\epsilon }_{0})}\), e and m are the charge and mass of an electron, ϵ0 is the vacuum dielectric constant, ρ is the density of Ni sites, c is the speed of light, and E1 and E2 are the energy limits of integration. Magneto-optical spectroscopy was performed in the Faraday geometry at cryogenic temperatures (4.0 K) in a capacitor-driven 65 T pulsed magnet at the National High Magnetic Field Laboratory in Los Alamos, NM. Our focus was on the 0.75–2.6 eV range with 2.4 meV resolution. Broadband light from a tungsten lamp was coupled to optical fibers and focused onto the sample for transmittance experiments. A collection fiber brought the light from the top of the probe to the grating spectrometer, where both charge-coupled device and InGaAs detectors were employed as appropriate. Spectra were taken in four different measurement configurations: (+H, up k), (−H, up k), (+H, down k), and (−H, down k). Each run was carried out sequentially and consistently, starting with one k direction (and pulsing to obtained both ±H) and then switching to the other k direction (again measuring both H directions). To switch k, we swapped the optical fibers from the source to the detector and vice versa. Specific care has been taken to make sure none of the reported effects come from the optical elements in the magneto-spectroscopy setup (such as trivial Faraday rotation in the optical fibers, etc.). The measurement configurations and data treatment were identical for both the magnetochiral and transverse magnetochiral cases.
First-principles DFT calculations were performed using the wien2k full-potential code46; the Ceperley-Alder local density approximation functional47, \(R{K}_{\max }=7.0\), and a 10 × 10 × 10 k-grid sampling were employed. Information on crystal fields and single-particle dipole matrix elements Pα within the Ni d-orbitals were extracted by employing orbital projectors implemented in the Embedded DMFT Functional (EDMFT) code48. Exact diagonalization (ED) routine, implemented within the EDMFT code, was used to obtain local multiplet eigenstates. Therein, crystal fields, spin–orbit coupling, and local exchange fields to incorporate magnetic order were included in the ED problem in addition to fully rotationally invariant Coulomb interactions. Directions of local exchange fields were adopted from ref. 48, where field-dependent magnetic configurations were computed from a first-principles-based magnetic exchange Hamiltonian. Local exchange fields (0.1 eV) were used in ED routine, where the strength was estimated by a separate magnetic DMFT calculation on Ni3TeO6 (T = 580 K). Finally, electric and magnetic-dipole matrix elements \({{\bf{P}}}^{n0}\equiv \left\langle n\right|{{\bf{P}}}_{\alpha }\left|0\right\rangle\) and \({{\bf{M}}}^{n0}\equiv \left\langle n\right|{\bf{M}}\left|0\right\rangle\) were computed using the ED eigenstates \(\left|0\right\rangle\) and \(\left|n\right\rangle\) obtained from above procedure.
In practice, instead of Pn0, we used matrix elements of the momentum operator pn0 to compute the response tensors; these are related by Pn0 = pn0(qe/imeωn0), where qe and me are the charge and mass of the electron, respectively. The optic subprogram49 in the wien2k package was employed to obtain the momentum matrix elements in band basis first, which were then transformed into the multiplet representation pn0 based on the knowledge of the ED eigenstates and local d-orbital projectors. It is noteworthy that the same procedure was applied to obtain Mn0 ≡ Ln0 + 2Sn0, where the g-factor has been set to be 2.
Four linear-response tensors—electro-electric (\({\chi }_{\alpha \beta }^{{\rm{ee}}}\)), electro-magnetic (\({\chi }_{\alpha \beta }^{{\rm{em}}}\)), magneto-electric (\({\chi }_{\alpha \beta }^{{\rm{me}}}\)), and magneto-magnetic (\({\chi }_{\alpha \beta }^{{\rm{mm}}}\))—can be computed with the quantities obtained above. These are defined according to the constitutive relations for the D and B fields,
Explicit forms for the magnetoelectric response tensors χme and χem were already given in Eq. (2), and the corresponding expressions for the electric and magnetic susceptibilities, which were used to compute the absorption spectra, are
Then the refractive index for light propagating along z ∥ c can be calculated as1,42,43,
where sk is the sign of the k-vector. Plugging this expression for the refractive index into the first line of Eq. (1) yields the second line of Eq. (1) in the manuscript.
Note that Eq. (6) above, and also Eq. (1), best apply when the propagating light is an eigenmode of the system. For unpolarized light experiencing polarization rotation, the size of the nonreciprocal dichroism signal should be smaller than that expected from Eq. (1). As shown in ref. 45, for mixtures of eigenmodes, an additional term appears proportional to the sample thickness and involving the ratios between the diagonal and off-diagonal elements of the electric and magnetic response tensors. This term is quite small, however, because those ratios are of order 10−3 according to our calculations. As our sample thickness is about 40 μm, about ≤102 times the wavelength, Eq. (1) is still expected to be a good first-order approximation to the nonlinear dichroismic absorption.
The strength of the spin–orbit coupling within the Ni d shell was estimated via a Wannierization routine50,51 implemented in the openmx code52. The estimated size of the spin–orbit coupling within the Ni t2g shell was about 42 meV. The contribution from Te was estimated to be about 10 meV from a separate estimation of the spin–orbit coupling in Ni3SO6 (assuming the spin–orbit coupling from sulfur is almost negligible). Magnetic orders were incorporated in the form of effective exchange fields exerted upon each site originating from the surrounding magnetic background. The directions of the effective exchange fields, e.g., the directions of the Ni magnetic moments in each magnetic configuration under the external field, were employed from ref. 37. The size of the exchange field was chosen to be 50 meV and the results do not visibly depend on this size once the splitting of the ground states becomes larger than the thermal energy scale (T ≲ 10 K in this work). The detailed computational method will be published elsewhere53.
Data availability
Data are available from the corresponding author upon reasonable request.
References
Kézsmárki, I. et al. One-way transparency of four-coloured spin-wave excitations in multiferroic materials. Nat. Commun. 5, 3203 (2014).
Tokura, Y. & Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 9, 3740 (2018).
Cheong, S.-W., Talbayev, D., Kiryukhin, V. & Saxena, A. Broken symmetries, non-reciprocity, and multiferroicity. npj Quantum Mater. 3, 19 (2018).
Qin, F. et al. Superconductivity in a chiral nanotube. Nat. Commun. 8, 14465 (2017).
Krstić, V. et al. Magneto-chiral anisotropy in charge transport through single-walled carbon nanotubes. J. Chem. Phys. 117, 11315–11319 (2002).
Aoki, R., Kousaka, Y. & Togawa, Y. Anomalous nonreciprocal electrical transport on chiral magnetic order. Phys. Rev. Lett. 122, 057206 (2019).
Kwon, J. H. Giant nonreciprocal emission of spin waves in Ta/Py bilayers. Sci. Adv. 2, e1501892 (2016).
Stock, C. et al. Spin-wave directional anisotropies in antiferromagnetic Ba3NbFe3Si2O14. Phys. Rev. B 100, 134429 (2019).
Nomura, T. et al. Phonon magnetochiral effect. Phys. Rev. Lett. 122, 145901 (2019).
Kravchuk, V. P., Rößler, U. K., van den Brink, J. and Garst, M. Solitary wave excitations of skyrmion strings in chiral magnets. Preprint at https://arxiv.org/abs/1902.01420 (2019).
Szaller, D., Bordács, S. & Kézsmárki, I. Symmetry conditions for nonreciprocal light propagation in magnetic crystals. Phys. Rev. B 87, 014421 (2013).
Kézsmárki, I. et al. Enhanced directional dichroism of terahertz light in resonance with magnetic excitations of the multiferroic Ba2CoGe2O7 oxide compound. Phys. Rev. Lett. 106, 057403 (2011).
Bordács, S. et al. Unidirectional terahertz light absorption in the pyroelectric ferrimagnet CaBaCo4 O7. Phys. Rev. B 92, 214441 (2015).
Rikken, G. L. J. A., Strohm, C. & Wyder, P. Observation of magnetoelectric directional anisotropy. Phys. Rev. Lett. 89, 133005 (2002).
Bordács, S. et al. Chirality of matter shows up via spin excitations. Nat. Phys. 8, 734–738 (2012).
Saito, M., Taniguchi, K. & Arima, T.-h Gigantic optical magnetoelectric effect in CuB2O4. J. Phys. Soc. Jpn 77, 013705 (2008).
Saito, M., Ishikawa, K., Taniguchi, K. & Arima, T. Magnetic control of crystal chirality and the existence of a large magneto-optical dichroism effect in CuB2O4. Phys. Rev. Lett. 101, 117402 (2008).
Rikken, G. L. J. A. & Raupach, E. Observation of magneto-chiral dichroism. Nature 390, 493–494 (1997).
Sessoli, R. et al. Strong magneto-chiral dichroism in a paramagnetic molecular helix observed by hard X-rays. Nat. Phys. 11, 69–74 (2015).
Nakagawa, N. et al. Magneto-chiral dichroism of CsCuCl3. Phys. Rev. B 96, 121102 (2017). (R).
Train, C., Gruselle, M. & Verdaguer, M. The fruitful introduction of chirality and control of absolute configurations in molecular magnets. Chem. Soc. Rev. 40, 3297–3312 (2011).
Barron, L. D. Chirality and magnetism shake hands. Nat. Mater. 7, 691–692 (2008).
Train, C. et al. Strong magneto-chiral dichroism in enantiopure chiral ferromagnets. Nat. Mater. 7, 729–734 (2008).
Sheu, Y. M. et al. Picosecond creation of switchable optomagnets from a polar antiferromagnet with giant photoinduced Kerr rotations. Phys. Rev. X 9, 031038 (2019).
Yu, S. et al. High-temperature terahertz optical diode effect without magnetic order in polar FeZnMo3 O8. Phys. Rev. Lett. 120, 037601 (2018).
SoljaČiĆ, M. & Joannopoulos, J. D. Enhancement of nonlinear effects using photonic crystals. Nat. Mater. 3, 211–219 (2004).
Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Phys. 3, 91–94 (2009).
Saito, M., Ishikawa, K., Taniguchi, K. & Arima, T.-h Magnetically controllable CuB2O4 phase retarder. Appl. Phys. Express 1, 121302 (2008).
Kézsmárki, I. et al. Optical diode effect at spin-wave excitations of the room-temperature multiferroic BiFeO3. Phys. Rev. Lett. 115, 127203 (2015).
Lee, J. H., Kézsmárki, I. & Fishman, R. S. First-principles approach to the dynamic magnetoelectric couplings for the non-reciprocal directional dichroism in BiFeO3. New J. Phys. 18, 043025 (2016).
Takahashi, Y. et al. Magnetoelectric resonance with electromagnons in a perovskite helimagnet. Nat. Phys. 8, 121–125 (2012).
Jung, J. H. et al. Optical magnetoelectric effect in the polar GaFeO3 ferrimagnet. Phys. Rev. Lett. 93, 037403 (2004).
Arima, T. Magneto-electric optics in non-centrosymmetric ferromagnets. Matter 20, 434211 (2008).
Toyoda, S. et al. One-way transparency of light in multiferroic CuB2O4. Phys. Rev. Lett. 115, 267207 (2015).
Saito, M., Ishikawa, K., Konno, S., Taniguchi, K. & Arima, T. Periodic rotation of magnetization in a non-centrosymmetric soft magnet induced by an electric field. Nat. Mater. 8, 634–638 (2009).
Oh, Y. S. et al. Non-hysteretic colossal magnetoelectricity in a collinear antiferromagnet. Nat. Commun. 5, 3201 (2014).
Kim, J. W. et al. Successive magnetic-field-induced transitions and colossal magnetoelectric effect in Ni3TeO6. Phys. Rev. Lett. 115, 137201 (2015).
Živkovć, I., Prša, K., Zaharki, O. & Berger, H. Ni3TeO6−a collinear antiferromagnet with ferromagnetic honeycomb planes. J. Phys. Condens. Matter 22, 056002 (2010).
Wang, X., Huang, F.-T., Yang, J., Oh, Y. S. & Cheong, S.-W. Interlocked chiral/polar domain walls and large optical rotation in Ni3 TeO6. APL Mater. 3, 076105 (2015).
Yokosuk, M. O. et al. Magnetoelectric coupling through the spin flop transition in Ni3TeO6. Phys. Rev. Lett. 117, 147402 (2016).
Cheong, S.-W. SOS: symmetry-operational similarity. npj Quantum Mater. 4, 53 (2019).
Miyahara, S. & Furukawa, N. Nonreciprocal directional dichroism and toroidalmagnons in helical magnets. J. Phys. Soc. Jpn 81, 023712 (2012).
Muthukumar, V. N., Valent, R. & Gros, C. Theory of nonreciprocal optical effects in antiferromagnets: the case of Cr2O3. Phys. Rev. B 54, 433–440 (1996).
Hlinka, J. Eight types of symmetrically distinct vectorlike physical quantities. Phys. Rev. Lett. 113, 165502 (2014).
Szaller, D. et al. Effect of spin excitations with simultaneous magnetic- and electric-dipole character on the static magnetoelectric properties of multiferroic materials. Phys. Rev. B 89, 184419 (2014).
Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, D. & Luitz, J. WIEN2k, An augmented plane wave + local orbitals program for calculating crystal properties (Karlheinz Schwarz, Techn. Universität Wien, Austria, 2001).
Ceperley, D. M. & Alder, B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566–569 (1980).
Haule, K. Structural predictions for correlated electron materials using the functional dynamical mean field theory approach. J. Phys. Soc. Jpn 87, 041005 (2018).
Ambrosch-Draxl, C. & Sofo, J. O. Linear optical properties of solids within the full-potential linearized augmented planewave method. Comp. Phys. Commun. 175, 1–14 (2006).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Weng, H., Ozaki, T. & Terakura, K. Revisiting magnetic coupling in transition-metal-benzene complexes with maximally localized Wannier functions. Phys. Rev. B 79, 235118 (2009).
Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 67, 155108 (2003).
Kim, H.-S., Yokosuk, M. O., Musfeldt, J. L., Haule, K. & Vanderbilt, D. unpublished.
Acknowledgements
Research at the University of Tennessee and Rutgers University is supported by the NSF-DMREF program (DMR-1629079 and DMR-1629059). A portion of this research was performed at the National High Magnetic Field Laboratory which is supported by the National Science Foundation DMR-1644779, the State of Florida, and the US Department of Energy.
Author information
Authors and Affiliations
Contributions
M.O.Y. and J.L.M. designed the study. J.Y. and S.W.C. grew the crystals, M.O.Y. polished the samples, and J.W.K. and S.W.C. confirmed the mono-chiral domain character of the polished crystals. M.O.Y., J.L.M., and S.W.C. discussed the measurement configurations and run pattern in detail. M.O.Y., K.D.H., K.R.O., S.A.C., A.V.S., and J.L.M. performed the pulsed field optical measurements, and M.O.Y. and J.L.M. analyzed the spectral data. H.S.K., K.H., and D.V. developed a microscopic model for nonreciprocal optical effects and applied it to Ni3TeO6. M.O.Y., H.S.K., K.H., D.V., and J.L.M. wrote the manuscript. All authors commented on the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yokosuk, M.O., Kim, HS., Hughey, K.D. et al. Nonreciprocal directional dichroism of a chiral magnet in the visible range. npj Quantum Mater. 5, 20 (2020). https://doi.org/10.1038/s41535-020-0224-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0224-6
This article is cited by
-
Trompe L’oeil Ferromagnetism—magnetic point group analysis
npj Quantum Materials (2023)
-
Confirming the trilinear form of the optical magnetoelectric effect in the polar honeycomb antiferromagnet Co2Mo3O8
npj Quantum Materials (2022)
-
Visualizing rotation and reversal of the Néel vector through antiferromagnetic trichroism
Nature Communications (2022)
-
Nonreciprocal directional dichroism at telecom wavelengths
npj Quantum Materials (2022)
-
Permutable SOS (symmetry operational similarity)
npj Quantum Materials (2021)