Abstract
The spin-\(\frac{1}{2}\) kagome antiferromagnet is considered an ideal host for a quantum spin liquid (QSL) ground state. We find that when the bonds of the kagome lattice are modulated with a periodic pattern, new quantum ground states emerge. Newly synthesized crystalline barlowite (Cu4(OH)6FBr) and Zn-substituted barlowite demonstrate the delicate interplay between singlet states and spin order on the spin-\(\frac{1}{2}\) kagome lattice. Comprehensive structural measurements demonstrate that our new variant of barlowite maintains hexagonal symmetry at low temperatures with an arrangement of distorted and undistorted kagome triangles, for which numerical simulations predict a pinwheel valence bond crystal (VBC) state instead of a QSL. The presence of interlayer spins eventually leads to an interesting pinwheel q = 0 magnetic order. Partially Zn-substituted barlowite (Cu3.44Zn0.56(OH)6FBr) has an ideal kagome lattice and shows QSL behavior, indicating a surprising robustness of the QSL against interlayer impurities. The magnetic susceptibility is similar to that of herbertsmithite, even though the Cu2+ impurities are above the percolation threshold for the interlayer lattice and they couple more strongly to the nearest kagome moment. This system is a unique playground displaying QSL, VBC, and spin order, furthering our understanding of these highly competitive quantum states.
Similar content being viewed by others
Introduction
Identifying the ground state for interacting quantum spins on the kagome lattice is an important unresolved question in condensed matter physics, owing to the great difficulty in selecting amongst competing states that are very close in energy. Antiferromagnetic (AF) spins on this lattice are highly frustrated, and for spin \(S=\frac{1}{2}\) systems the ground state does not achieve magnetic order and is believed to be a quantum spin liquid (QSL)1,2,3,4,5,6,7,8,9. The QSL is an unusual magnetic ground state, characterized by long-range quantum entanglement of the spins with the absence of long-range magnetic order10,11,12,13. The recent identification of herbertsmithite (Cu3Zn(OH)6Cl2)14,15,16,17 as a leading candidate QSL material has ignited intense interest in further understanding similar kagome materials.
For the ideal \(S=\frac{1}{2}\) kagome nearest-neighbor Heisenberg model, theoretical calculations point toward various QSL ground states (gapped and ungapped), though the exact ground state is still a matter of great debate1,2,3,4,5,6,7,8,9,18,19,20. Moreover, early calculations indicated that a valence bond crystal (VBC) state is a close rival to the QSL21,22,23,24. However, real kagome materials often have additional interactions that relieve the frustration and drive the moments to magnetically order25,26, indicating that the ground state depends sensitively on small perturbations and lattice distortions. Here, we present a material system in which small changes can be made to the kagome lattice, thereby revealing closely related QSL, VBC, and spin-ordered states. Importantly, we make close connection with theory by performing numerical simulations for the quantum moments based on the specific symmetry of the material.
In herbertsmithite, the kagome layers are separated by non-magnetic Zn2+ ions, which preserves the two-dimensional character of the magnetic layers. The kagome layers stack in an ABC sequence. While Zn2+ does not mix onto the highly Jahn–Teller distorted Cu2+ kagome sites, up to 15% Cu2+ can mix onto the interlayer Zn2+ sites27, which complicates the observations of intrinsic QSL behavior28. Barlowite (Cu4(OH)6FBr) is another recently discovered mineral with layered Cu2+ kagome planes that are stacked in an AA sequence, different from herbertsmithite29. The Cu2+ moments between the kagome layers cause long-range magnetic order at TN ≈ 10–15 K, much smaller than the Curie–Weiss temperature of Θ ≈ −130 K30,31,32,33. The magnetic structure of orthorhombic barlowite has been interpreted using conflicting models based on neutron powder diffraction (NPD) data34,35. The precise determination of the magnetic order is made challenging by the weak cross-section of \(S=\frac{1}{2}\) Cu2+ moments, and the stronger Bragg peaks available from single-crystal measurements would be an important improvement.
While barlowite itself is an intriguing quantum magnet, it is also the parent of a QSL candidate, Zn-substituted barlowite, whose stability was first predicted by first-principles calculations36,37. Substituting barlowite’s interlayer site with Zn2+ isolates the Cu2+ kagome layers, leading to Cu3ZnxCu1−x(OH)6FBr. Calculations also predict significantly fewer magnetic Cu2+ “impurities” on the interlayer site than in herbertsmithite, making it an attractive material to study36. Polycrystalline samples show no magnetic order, and we find its Curie–Weiss temperature to be as large as Θ = −253 K. A gapped ground state with Z2 topological order has been proposed34,38,39. The first single crystals of Zn-substituted barlowite were recently synthesized with x = 0.33, which suppresses magnetic order to T = 4 K33. Our new synthesis techniques produce large single crystals of barlowite and Zn-substituted barlowite, and measurements of the magnetic and structural properties allow for detailed studies of how the QSL tendencies on the \(S=\frac{1}{2}\) kagome lattice are affected by subtle structural symmetry lowering and magnetic impurities on the interlayer sites.
Results
New high-symmetry barlowite: a pinwheel modulated kagome lattice
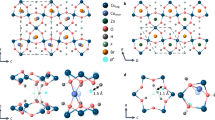
The low-temperature symmetry of the previously studied barlowite (denoted barlowite 1) has been subject to differing interpretations30,31,32,34,35,40,41. We performed a comprehensive structural investigation employing a combination of high-resolution synchrotron powder and single-crystal X-ray diffraction (PXRD and SCXRD), as well as NPD to definitively determine the structure of barlowite 1, which transforms to orthorhombic Pnma below T ≈ 265 K (Supplementary Figs. 2–4, Supplementary Tables 2, 3, 5–8, 10, and 11). Figure 1b shows the emergence of superlattice peaks and orthorhombic peak splitting related to this transition. We have also grown sizable single crystals of a different variant of barlowite using a new chemical reaction33. Intriguingly, these crystalline samples (denoted barlowite 2) have a low-temperature structure distinct from that of barlowite 1, belonging to the higher-symmetry hexagonal space group P63/m. X-ray precession images (Supplementary Fig. 1) exhibit the emergence of superlattice peaks consistent with this space group, and no orthorhombic splitting is observed (Fig. 1c, Supplementary Figs. 5 and 6, Supplementary Table 9)—ruling out any orthorhombic distortion down to 20 times smaller than in barlowite 1. In the following, all peaks are indexed according to the high-temperature space group (P63/mmc). Figure 1d shows a superlattice peak measured via elastic neutron scattering in a single-crystal sample of barlowite 2. The inset shows the temperature dependence of the integrated intensity from both longitudinal and transverse scans (Fig. 1d and Supplementary Fig. 20, respectively), indicating that the structural transition occurs at T ≈ 262(8) K. The fitted width of the superlattice peak (Supplementary Table 17) indicates an in-plane domain size of ~61 Å assuming a finite-size domain model42.
a Schematic showing the two phase transitions of barlowite 1 and 2. The interlayer occupancy values are taken from SCXRD (Supplementary Table 3). b PXRD patterns from T=90K to 300K showing a Pnma superlattice peak and orthorhombic splitting in barlowite 1. c PXRD patterns from T=90K to 300K showing no visible P63/m superlattice peak nor orthorhombic splitting in barlowite 2. Bragg reflections of Pnma and P63/m, respectively, at T=90K are indicated by blue tick marks. d Elastic neutron scattering on single crystalline barlowite 2 with Ei=5meV showing the temperature dependence of the P63/m superlattice peak [0.5 1.5 0]. The notation of the high-temperature space group P63/mmc is used to index peaks. Inset: temperature dependence of the integrated intensity measured along the longitudinal and transverse directions of the wavevector \(\bf{Q}\) in the scattering plane with Ei=5 and Ei=14.7meV, respectively, indicating that the structural transition occurs at T=262(8)K. Uncertainties are statistical in origin and represent one standard deviation.
In both variants of barlowite, the structural phase transition is characterized by changes in the relative occupancies of the interlayer Cu2+ site, summarized in Fig. 1a. At T = 300 K, the interlayer Cu2+ is disordered with equal occupancy over three symmetry-equivalent sites with distorted trigonal prismatic coordination (point group C2v). Below the phase transition in barlowite 1, we find that the interlayer Cu2+s become disordered over three symmetry-inequivalent sites with unequal occupancies (Fig. 1a). The much higher resolution of our new synchrotron XRD data compared to NPD may explain why these occupancies have not been reported in previous structural models34,35,40. For our fit results, see Supplementary Tables 3 and 8. In barlowite 2, the superlattice unit cell is doubled along the a- and b-axes. As shown in Fig. 1a, two of the eight interlayer Cu2+ locations have equal occupancy of the three sites, while the remaining six Cu2+ locations have unequal occupancies. Barlowite 2 has a much less drastic difference in relative occupancy compared to barlowite 1, reflecting higher similarity with the high-temperature structure and less symmetry breaking.
While kagome materials often undergo structural transitions upon cooling that relieve the frustration43,44, in barlowite the kagome layer remains substantially intact throughout the transition. At room temperature, there is only one kagome Cu2+ site, forming equilateral triangles on the ideal kagome lattice. In both lower symmetry space groups, there are two distinct kagome Cu2+ sites; thus, there are slight variations in the Cu–Cu distances—on the order of 0.01 Å (Supplementary Table 1). In barlowite 1, all kagome triangles are distorted, with the Cu–O–Cu kagome bond angles varying by ±1.2∘. In barlowite 2, two kagome equilateral triangles exist in the supercell with identical Cu–O–Cu kagome bond angles, and the other six triangles are only slightly distorted with bond angles varying by ±0.8∘ around their triangles. In principle, these slight changes in bond lengths and bond angles should lead to different magnitudes of the magnetic exchange interaction, though the differences may be small. Most interestingly, the bonds form a pinwheel-type pattern, as depicted in Fig. 2. Also depicted are the bond patterns in barlowite 1, which has a strong orthorhombic distortion, and also in Zn-substituted barlowite (Cu3ZnxCu1–x(OH)6FBr with x > \(\gtrsim\) 0.5), which has the ideal kagome lattice.
Structural and magnetic characteristics are tabulated. The second to last row shows the magnetic interactions on the kagome planes of barlowite 1, barlowite 2, and Zn-substituted barlowite. The thickness of the line indicates bond strength as expressed through its Cu–O–Cu bond angle. In barlowite 2, the variation in angle of ±0.8∘ is quite small, so the differences in magnetic exchange are also likely small. In Zn0.56 and Zn0.95, the kagome motif consists only of equilateral triangles (green); however, in barlowite 2 the kagome motif is expanded due to a mix of equilateral (green) and distorted (red/blue) triangles. On the other hand, barlowite 1 is more distorted, containing only distorted triangles.
Understanding the ground state physics with numerical simulations
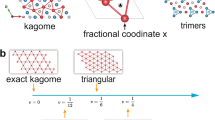
To explore the possible magnetic ground states stemming from these distinct structures, we investigated the ground state properties of the distorted Heisenberg model with Hamiltonian \(H\,=\,\mathop{\sum}\nolimits_{(i,j)}J_{ij}{\text{S}}_{i}\cdot{\text{S}}_{j}\) on the kagome lattice using the density-matrix renormalization group (DMRG) technique45. Our results for the isotropic case (Jij = J) are consistent with the ground state of the system being a QSL (Fig. 3c), as expected. We further calculated the model with couplings extracted from barlowite 1 and barlowite 2, with spatial anisotropy \(J^{\prime} \;<\; J\) as illustrated in Fig. 3. While the longer range and interlayer magnetic couplings are neglected, as well as the Dzyaloshinskii–Moriya (DM) interaction and exchange anisotropy, due to numerical limitations, the simplified model captures essential features of the magnetic correlations in the kagome layer.
a Illustration of a simplified \(J-J^{\prime}\) Heisenberg model for barlowite 1. The six-site unit cell is in the middle panel, and the bond pattern for \(J^{\prime} =0.8J\) is shown in the left panel on a cylinder consisting of 16 × 4 unit cells (192 sites), where the bond thickness denotes the absolute value of \(\left\langle {{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\right\rangle\). The corresponding spin structure factor S(q) in the right panel has a sharp peak at momentum [1 1 0]. b Illustration of a simplified \(J-J^{\prime}\) Heisenberg model for barlowite 2. The 12-site unit cell is in the middle panel, and the bond pattern for \(J^{\prime} =0.95J\) is given in the left panel. The cylinder consists of 24 × 4 unit cells (288 sites). The spin structure factor S(q) in the right panel has a broad peak at momentum [1 0 0]. Here, the yellow lines denote bonds with interaction \(J^{\prime}\), while the black lines are bonds with interaction J. c The isotropic Heisenberg model with \(J^{\prime} =J\) and the corresponding uniform bond pattern in the QSL phase. The cylinder consists of 16 × 4 unit cells. d Schematic phase diagram of the \(J-J^{\prime}\) Heisenberg model as a function of \(J^{\prime} /J\), where the dashed line \({J}_{c}^{\prime}=0.998(1)\) denotes the phase boundary between the pinwheel VBC and QSL phases. The spin gap Δs of the \(J^{\prime} =0.95J\) point in the pinwheel VBC phase is plotted in the right panel, as a function of the inverse diameter of the cylinder. Error bars represent the confidence interval in the fitting procedure corresponding to ±σ (σ is the standard deviation).
To make predictions for experimental measurements of the magnetic correlations, the equal-time spin structure factor \(S(q)=\frac{1}{N}{\sum }_{i,j}\left\langle {{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\right\rangle {e}^{-iq({r}_{i}-{r}_{j})}\) is calculated. As shown in Fig. 3a, the simplified model for barlowite 1 yields a very sharp peak at [1 1 0], implying a strong magnetic ordering tendency. In contrast, the simplified model for barlowite 2 only exhibits a very broad peak (Fig. 3b, indicating gapped spin excitations with exponentially decaying spin–spin correlations. The pinwheel singlet pattern is consistent with a 12-site VBC state, which is a close rival to the QSL state proposed in early calculations21,22,23,24. In Fig. 3d, we show the phase diagram of the J − \(J^{\prime}\) Heisenberg model on the kagome lattice as a function of \(J^{\prime} /J\), where a phase transition between the pinwheel VBC order and the QSL state is found around \(J^{\prime} \approx 0.998(1)J\). The nature of the phase transition observed here is first order (Supplementary Fig. 25); this is similar to the transition between the QSL and a 36-site VBC demonstrated in a previous study5. That this transition occurs so close to \(J^{\prime} /J=1\) clearly demonstrates the close proximity of the ground state energies of the pinwheel VBC and the QSL. In addition, the calculated value for the spin gap of the pinwheel VBC is ~0.15J; this was calculated deeper in the VBC phase at \(J^{\prime} /J=0.95\).
The model’s prediction that barlowite 1 has a spin-ordered ground state is borne out by experimental results30,31,32,33. While we do not observe long-range magnetic order in the kagome plane, it may be induced by ferromagnetic (FM) coupling to interlayer spins46. On the other hand, the model for barlowite 2 predicts a VBC ground state, although the model neglects the coupling to interlayer spins—which undoubtedly play a role. We also neglect the effects of the DM interaction and exchange anisotropy, which exist in similar materials47, but the values for these interactions in barlowite have not yet been determined. Therefore, barlowite 1 and 2 should have substantially different phase transitions, since the preferred ground states on the kagome planes have different symmetries, as we explore below.
Quantum magnetism of barlowite 2: accommodating the pinwheel modulation
Magnetic susceptibility measurements on barlowite 1 and 2 (Fig. 4a) illustrate the significant differences between the two variants. While barlowite 1 has a transition at TN ≈ 16 K, barlowite 2 has two transitions: a broad transition at TN1 ≈ 10 K and a second, sharp transition at TN2 ≈ 6 K. The heat capacity and entropy related to the magnetic transitions (Cmag and S) of single crystalline barlowite 2 have a gradual onset of short-range order that clearly becomes significant well below T = 16 K (Fig. 4d, Supplementary Fig. 16). For both 1 and 2, the entropy change associated with the magnetic transition is ~1/4 of the expected value for the four Cu2+s in the formula unit, implying that the interlayer Cu2+ precipitates the order33. In an applied field, the transition broadens and shifts to lower temperature with a crossover at T ≈ 10 K, similar to the TN1 of 2.
a The real part of the AC susceptibility (χ′) of polycrystalline, orthorhombic barlowite 1 and a collection of single crystals of hexagonal barlowite 2. b The real part of the AC susceptibility (χ′) of a 2.0 mg single crystal of barlowite 2 aligned in the ab plane and along the c-axis. c Aligned magnetization (M) as a function of applied field at T = 2 K for single crystals of barlowite 2 and 1 (from ref. 32). d Heat capacity associated with the magnetic transitions (Cmag) of barlowite 2 calculated as C − Cbg (Supplementary Fig. 16). The dashed black lines denote the magnetic transitions of barlowite 2: TN1 = 10 K and TN2 = 6 K. Error bars represent the confidence interval in the fitting procedure corresponding to ±σ (σ is the standard deviation). Note: 1 emu (mol Oe)−1 = 4π10−6 m3 mol−1.
Our single crystals of barlowite 2 are large enough for AC susceptibility (χ′) and DC magnetization (M) measurements, revealing significant anisotropy (Fig. 4b, c and Supplementary Figs. 11 and 12). A net FM moment arises in the ab plane, while the susceptibility along the c-axis remains suppressed through the two magnetic transitions. The magnetization shows a similar story: at T = 2 K, there is hysteresis when μ0H is parallel to the ab plane, but not when μ0H is along the c-axis. At T = 20 K, above the magnetic transitions, the two orientations are nearly identical. While the overall interactions in the kagome layers are AF (Curie–Weiss temperature Θ = −114(1) K; see Supplementary Table 15), there is a net FM moment of ~0.11 μB per formula unit in the magnetically ordered, low-temperature state, obtained as the height of the hysteresis loop. The FM moment is approximately three times smaller than the net moment of barlowite 1 (Fig. 4c), indicating a more fragile spin-ordered state.
To directly determine the magnetic structure, we coaligned 1115 deuterated crystals for magnetic neutron diffraction measurements. A large sample is required since the ordered moment is small and the measured magnetic Bragg peaks are weak. Strikingly, half-integer and integer magnetic Bragg peaks exhibit distinct behavior. Figure 5a shows a comparison of longitudinal scans through the [0.5 0.5 0] and [1 0 0] magnetic Bragg peaks. Half-integer peaks are noticeably broader than integer peaks and have enhanced background scattering (Supplementary Fig. 21, Supplementary Table 17). After deconvolving the instrumental resolution, the typical domain size extracted using a finite-size domain model42 for the half-integer peaks is ~118 Å, while the integer peaks yield a much larger domain size > 360 Å (close to the limit of instrument resolution). Their peak intensities also have distinct temperature dependences below T ≈ 10 K, the TN1 observed in AC susceptibility (Fig. 5b, Supplementary Fig. 19). The [0.5 0.5 0] peak increases smoothly below T ≈ 10 K, matching M2 measured via magnetization. However, the integer peaks are extremely weak in the intermediate temperature range 6 K < T < 10 K and only rise rapidly below T ≈ 6 K (TN2) as resolution-limited peaks. This indicates that the two transitions denote the ordering of two sets of moments, which we identify with interlayer moments that have short-range order below TN ≈ 10 K and kagome moments that have long-range order below TN2 ≈ 6 K. This is consistent with the magnetic structure factor calculations that we discuss below.
a Longitudinal scans through the [0.5 0.5 0] and [1 1 0] magnetic Bragg peaks measured at T = 2.7 and 8 K with Ei = 5 meV at SPINS, where the T = 20 K data was subtracted as background. The red lines are Gaussian fits. The horizontal bars indicate the experimental resolution, and the error bars represent one standard deviation. b Temperature dependences of the peak intensities of the [0.5 0.5 0] and [1 1 0] magnetic Bragg peaks measured at E = 5 meV (SPINS) and Ei = 14.7 meV (BT-7). The top panel also displays the squared magnetization (M2) of a single crystal in the ab plane at μ0H = 0.005 T. Below T = 6 K, the red line in the bottom panel is a power-law fit from T = 2–11 K with critical exponent β = 0.30(3) and TN = 6; above T = 6 K the line is a guide to the eye. c The pinwheel q = 0 magnetic model of barlowite 2 in the ab plane and along c (inset). d The magnetic model proposed for orthorhombic barlowite 1 by ref. 35 overlaid on our barlowite 1 crystal structure. All occupancy values are taken from SCXRD (Supplementary Table 3). For c and d, the arrows indicate the sizes and directions of the moments. Dark and light blue spins represent interlayer Cu2+s in different layers, while red and green spins represent kagome Cu2+s. Each interlayer motif is visualized by one spin at the weighted center of the sites. The thickness of the lines between kagome spins indicates relative bond strength extracted from the Cu–O–Cu bond angles. The ± symbols next to the kagome spins denote the directions of the out-of-plane component in the spins. The dashed lines denote the magnetic unit cell.
A simple spin configuration based on the structural symmetry is a variation of the q = 0 arrangement for the kagome Cu2+s, in which the spins on each triangle are oriented 120∘ to each other (Fig. 5c, Supplementary Figs 22 and 23, Supplementary Tables 18–22). Since there are two crystallographically distinct kagome Cu2+ sites—the sets of red and green spins—we allowed them to have different moment sizes and different in-plane rotation directions. The best magnetic structure based on these assumptions is depicted in Fig. 5c. Each set of distinct kagome spins has a local q = 0 arrangement with a relative angle of ~28∘ between them (a relative angle of zero would denote a perfect q = 0 arrangement). We call this a “pinwheel q = 0” state. In addition, parallel lines of spin in the kagome plane have an out-of-plane rotation angle of ~29∘ (determined by the intensity of the [1 1 1] magnetic Bragg peak). This out-of-plane tilting along lines is consistent with the allowed zero energy modes in a q = 0 structure with an easy-axis exchange anisotropy (here, the C3 rotational symmetry of the lattice is spontaneously broken). The net FM moment is 0.033 μB per formula unit, which is smaller than the FM moment of 0.11 μB per formula unit obtained from the magnetization; the difference may be related to the field-cooled protocol used to determine the FM moment. The magnetic peaks of barlowite 2 are considerably weaker than those observed in barlowite 134,35, supporting its closer proximity to the QSL ground state.
While seemingly complicated, this magnetic structure is consistent with the underlying microscopic magnetic interactions. Ab initio calculations indicate a strong FM interaction between the interlayer spin and its NN kagome spin31. This FM interaction would compete with the AF interactions between kagome spins and perturb the perfect q = 0 configuration in the manner that we observe. We calculated the energy of various spin configurations including the AF J between kagome moments and the JFM between the interlayer and kagome moments. Based on our spin structure, the estimated FM couplings between the interlayer and kagome spins are indeed strong (−0.89J on average; see Supplementary Fig. 24), consistent with the previous calculations31. We find that the same microscopic rules are consistent with the spin structure for barlowite 1 (ref. 35; Fig. 5d), albeit with an orthorhombic magnetic configuration. For completeness, we also fit barlowite 2 with the orthorhombic spin structure proposed for barlowite 135 (Supplementary Tables 23–25); however, this model is not obviously compatible with the underlying crystal structure and interactions of barlowite 2. We note that the weak scattering from \(S=\frac{1}{2}\) moments limits the number of magnetic Bragg peaks observable in the single-crystal sample, so that the proposed spin structure, while consistent with the structural symmetry and interactions, is not necessarily unique.
We interpret the transitions at TN1 = 10 K and TN2 = 6 K in terms of a successive ordering of different spins. First, the interlayer spins begin ordering below TN1 since these moments mainly contribute to the half-integer magnetic peaks. The peak width indicates that they order with a short correlation length, consistent with the lack of a sharp anomaly in the heat capacity. This is followed at TN2 by sudden ordering of the kagome spins (Fig. 5b), which account for most of the integer peak intensity and thus display long-range order. The specific heat also begins to drop dramatically below TN2. The interlayer Cu2+ correlations are probably affected by the random occupancy of the interlayers at low temperatures. Even below the structural transition temperature, the kagome lattice remains nearly perfect, and the strong interactions between kagome Cu2+ moments can drive longer range correlations.
Structure and magnetism of the Zn-substituted QSL compositions: ideal kagome planes and robust QSL behavior
Substituting Zn into barlowite can yield polycrystalline samples with no magnetic order—the first step to a QSL candidate material38. We synthesized sizable single crystals of Zn-substituted barlowite and determined their crystal structure along with that of polycrystalline samples. Chemical analysis (ICP-AES) indicated the crystals’ composition is Cu3.44Zn0.56(OH)6FBr (denoted Zn0.56). A deuterated polycrystalline sample (denoted Zn0.95) has nearly a full equivalent of Zn, which is comparable to (but higher than) that reported in herbertsmithite27. The deuteration, which is important for neutron scattering measurements, does not have an appreciable effect on the magnetic behavior.
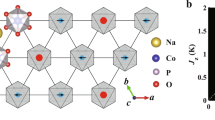
Neither compound demonstrates symmetry lowering down to the lowest temperatures measured, leading to perfect, undistorted kagome lattices. For polycrystalline Zn0.95, neutron and synchrotron X-ray data down to T = 3 K were co-refined in space group P63/mmc, and single crystalline Zn0.56 was measured with synchrotron XRD down to T = 90 K (Supplementary Figs. 1 and 7–10, Supplementary Tables 2, 4–7, and 12–14). While the interlayer Zn2+/Cu2+ in herbertsmithite occupy the same shared crystallographic site, in Zn-substituted barlowite the Zn2+ lies on a centered D3h position in perfect trigonal prismatic coordination, while the Cu2+ is equally disordered over the three off-center C2v sites (Fig. 6a). Rietveld refinements of the neutron data for Zn0.95 support this assignment, and it is consistent with the different Jahn–Teller activity of these ions. We determine that the average structure is hexagonal; however, we cannot exclude subtle local symmetry lowering or lattice distortions that evade X-ray crystallographic methods, which are sensitive to the bulk long-range order.
a Structures of Zn-substituted barlowite and herbertsmithite showing their interlayer metal coordination environments. The top–down view of Zn-substituted barlowite displays the coexistence of the centered (D3h) Zn2+ site and the set of triplicated off-center (C2v) Cu2+ interlayer sites, visualized in VESTA74. The top–down view of herbertsmithite shows its distinct interlayer coordination: there is only one site for both Zn2+ and Cu2+, and the kagome layers above and below the interlayer site are rotated by 60∘. In the top–down views, the atoms are displayed as thermal ellipsoids at 90% probability. F, Br, Cl, and H are not shown. b DC susceptibility (χ) measured in an applied field μ0H = 7 T of polycrystalline Zn0.95, a collection of single crystals of Zn0.56, and polycrystalline herbertsmithite. Also plotted is an estimate of the intrinsic susceptibility of the Zn-substituted barlowite kagome lattice. The amount of Cu2+ magnetic impurities in the herbertsmithite sample is estimated at 15%27. The inset shows the inverse susceptibility of the interlayer Cu2+ magnetic impurities; the line is a Curie–Weiss fit from T = 10–50 K with no diamagnetic correction χ0. c Aligned magnetization as a function of applied field for a 1.4 mg single crystal of Zn0.56. d Temperature dependence of C/T for Zn0.95 and eZn0.56 in applied fields of μ0H = 0–9 T. Note: 1 emu (mol Oe)−1 = 4π10−6 m3 mol−1.
Both compositions of Zn-substituted barlowite display a lack of magnetic order consistent with a QSL ground state, as shown in Fig. 6b. The susceptibility of single crystalline Zn0.56 is higher than that of polycrystalline Zn0.95 and herbertsmithite due to the higher concentration of magnetic impurities on the interlayer (~44% Cu2+). Interestingly, these results imply that even ~50% Zn2+ on the interlayer is sufficient to push the ground state toward a QSL. In herbertsmithite, the interlayer sites form a cubic superlattice, although only 15% are occupied by Cu2+—which is below the percolation limit of 0.3128,48. Here, the amount of magnetic Cu2+ impurities in Zn0.56 is well above this percolation limit, but long-range order is not observed.
Synthesizing two samples of Zn-substituted barlowite with different amounts of Zn allows us to quantify the impurity (interlayer Cu2+) contribution to the total susceptibility. By removing the impurity contribution, an estimate of the intrinsic susceptibility of the barlowite kagome lattice is revealed (Fig. 6b). The susceptibility of herbertsmithite (which has ~15% Cu2+ interlayer impurities27) nearly overlays that of the impurity-subtracted Zn0.56 at low temperatures, although they diverge slightly above T ≈ 50 K. Zn0.95 is very close to “pure,” and its largest deviations from impurity-subtracted Zn0.56 occur at the lowest temperatures, below T ≈ 20 K. The inverse susceptibility of the impurity contribution (Fig. 6b, inset) shows linear Curie–Weiss behavior below T = 50 K with a small AF Θ = −3 K, similar to herbertsmithite47,49. Assuming a μeff = 1.8 μB as observed in the other samples produced 0.45 Cu2+s, consistent with the 0.39 Cu2+s from chemical analysis. Curie–Weiss fits indicate that impurity-subtracted Zn0.56 has the most negative Θ = −253 K, signaling the highest degree of magnetic frustration in this family (Supplementary Table 15, Supplementary Figs. 13 and 14).
In single crystalline Zn0.56, the low-temperature magnetic response M vs. μ0H is anisotropic (Fig. 6c). The ab plane magnetization is higher than the c-axis magnetization, consistent with the trend in barlowite 2 that reflects the anisotropy of the interlayer Cu2+ moments. However, no hysteresis is observed, which further indicates the lack of magnetic ordering or freezing. The magnitude of the magnetization is approximately half that of barlowite 2, consistent with the significant Zn substitution of x = 0.56 on the interlayer. Curie–Weiss fits on oriented single crystalline barlowite 2 and Zn0.56 (Supplementary Fig. 15, Supplementary Table 16) confirm the clear magnetic anisotropy observed in the M vs. μ0H curves, with χc > χab at high temperatures—similar to herbertsmithite—which indicates the presence of easy-axis exchange anisotropy47,50.
Figure 6d, e show the specific heat plotted as C∕T vs. T of Zn0.95 and Zn0.56 from T = 0.1–10 K; C vs. T and T∕(μ0H) are plotted in Supplementary Fig. 17. The lack of a sharp anomaly in both samples (similar to herbertsmithite) is consistent with the absence of magnetic order. The low-temperature upturn in both samples can be attributed to a nuclear Schottky anomaly from Cu. Zn0.95 exhibits a broad feature below T ≈ 3 K that shifts to higher temperatures and broadens in an applied field, similar to observations in herbertsmithite51. Zn0.56 also exhibits a broad peak in C∕T, where the area under the curve shifts to higher temperature with increasing field. Interestingly, the area under the C∕T curve, which measures the change in entropy, is roughly similar in both Zn0.56 and Zn0.95 samples. Hence the degrees of freedom that give rise to this broad peak do not simply scale with the number of interlayer impurities. Supplementary Fig. 18 shows the suppression of magnetic order across the barlowite family in C vs. T. For Zn-substituted compositions Cu3ZnxCu1−x(OH)6FBr with x \(\gtrsim\) 0.5, the QSL signatures in the bulk properties appear surprisingly similar.
Discussion
Comparing the three flavors of the modulated kagome lattice (orthorhombic distorted, pinwheel, and uniform) leads to new insights about the competition between the quantum ground states. Single-crystal growth and combined high-resolution synchrotron X-ray and neutron diffraction (structural and magnetic) were key advances in obtaining these results. A summary of the interplay between the QSL, VBC, and magnetic order ground states in the barlowite family is shown in Fig. 7. First, we find that QSL behavior is surprisingly robust in Zn0.56 despite a substantial number of interlayer impurities. The magnetic susceptibility of the kagome moments is remarkably similar to herbertsmithite, even though we deduce that the interlayer magnetic impurities occupy lower symmetry sites in both Zn0.56 and Zn0.95. While the strong FM interlayer coupling to the kagome spins is responsible for the ordering in barlowite 2, no FM correlations are evident in Zn0.56 (nor Zn0.95), even though 44% of the interlayer sites contain Cu2+. A strong relative distinction of our Zn-substituted compositions is that the kagome lattice is not modulated, preferring to stabilize the QSL. Hence, it appears that once spins participate in the QSL wavefunction, they resist forming substantial correlations with impurity moments.
a Schematics of the magnetic state of barlowite 2; at T < 6 K the kagome layer has long-range pinwheel q = 0 order, and at 6 K < T < 10 K the kagome layer potentially has a pinned pinwheel valence bond crystal state. The interlayer moments are short-range ordered in both temperature ranges. b Schematic of the ground state in Zn-substituted barlowite (Cu3ZnxCu1−x(OH)6FBr, x ≳ 0.55). Neither the kagome nor the interlayer spins have appreciable magnetic order down to T = 0.1 K.
In barlowite 2, the subtle pattern of bond modulations is shown by DMRG calculations to prefer a VBC ground state—which has long been suspected to be close in energy to the QSL state. An interesting pinwheel VBC state has been previously observed52 in Rb2Cu3SnF12; however, that material has bond deformations that are over ten times larger than those we observe in barlowite 2. Here, we find that even a less than one percent modulation of the bonds results in a VBC ground state. We note that in barlowite 2, the VBC does not order spontaneously but is rather pinned by the preexisting lattice distortion. The additional coupling to the interlayer spins eventually induces a q = 0-type spin order, which is also known to be close in energy to the QSL phase. The q = 0 structure is adjacent to the QSL ground state in the phase diagram when second neighbor AF Heisenberg coupling and/or a DM interaction is included53,54,55.
Barlowite 2 has a new Hamiltonian that has not been studied as yet, consisting of minute deviations from the uniform kagome lattice. We may rationalize the magnetic transitions upon cooling in the following way. At high temperature, the spin fluctuations are likely very similar to those in the QSL phase (Zn-substituted barlowite with x ≳ 0.5). Below the structural phase transition, the distinction between J and \(J^{\prime}\) onsets gradually and likely selects VBC correlations at lower temperatures, although they are obscured by competing thermal effects. Below TN1 = 10 K, the interlayer spins begin to exhibit short-range order with a growing moment, which acts as a staggered internal magnetic field; once it grows strong enough to overcome the VBC correlations, it drives q = 0 order at TN2 = 6 K. Therefore in barlowite 2, we can identify two specific competing ground states—pinwheel VBC and pinwheel q = 0—which are adjacent to the QSL ground state of the neighboring Zn-substituted compounds.
Clearly, different synthetic routes significantly affect the morphology and low-temperature properties of barlowite, and this is a new lever to explore this quantum material33. The differences point to an additional level of complexity in the synthesis of Cu oxysalt minerals and calls for a re-examination of the existing characterization of this class of materials, which also includes claringbullite56,57,58 and clinoatacamite59,60,61, among others. The two distinct structures below T ≈ 265 K in the two variants of barlowite demonstrate a clear structure–properties relationship with the low-temperature magnetism.
The strong synergy between theory and experiment in \(S=\frac{1}{2}\) kagome systems makes comparisons between different kagome QSL candidates timely and intriguing10,11,12,13. Zn-substituted barlowite is only the second \(S=\frac{1}{2}\) kagome QSL compound after herbertsmithite; the main differences between these compounds are the slightly off-center location of the interlayer moments and the stacking sequence of the kagome layers. Comparing herbertsmithite and Zn-substituted barlowite not only furthers our understanding of the low energy behavior caused by slight imperfections (such as impurities, lattice distortions, or magnetic interactions beyond the idealized models), which are inherent in all QSL materials, but also illuminates the rich rivalry of ground states that compete with the exotic QSL ground state. The ability to realize specific patterns of modulated bonds on the kagome lattice opens the door to investigate possible new classes of modulated QSL states that break the lattice symmetry62.
In summary, we have made the first large single crystals of two compounds, which allows us unique access to their physics. Two resulting highlights are: (1) our discovery of VBC physics on a patterned kagome lattice close to the QSL, and (2) the robustness of QSL behavior on the uniform kagome lattice even in the presence of many interlayer impurities. We have additionally performed DMRG calculations to predict the ground state physics of the lattices that we determined. Finally, the quality of our structural analysis is unprecedented for the barlowite family, which is extremely important to understand these delicate phases. Convincing proof of new quantum phases requires strong evidence of sample quality, which we provide here. The universal magnetic behavior that we find in the two QSL compositions is exciting as the kagome QSLs are one of only a few physical systems that are believed to have long-range quantum entanglement.
Methods
All hydrothermal reactions were performed in PTFE-lined stainless steel autoclaves, and the products were recovered by filtration and washed with DI H2O. The reactions yielding barlowite 2 and Zn0.56 crystals also yielded polycrystalline LiF, which was removed by sonication in acetone. Barlowite 1 was synthesized33 by mixing Cu2(OH)2CO3 (Alfa, Cu 55%), NH4F (Alfa, 96%), HBr (Alfa, 48% wt), and 36 mL DI H2O (EMD Millipore) or D2O (Aldrich, 99.9%) in a 45 mL autoclave, which was heated over 3 h to 175 °C and held for 72 h before being cooled to room temperature over 48 h. Protonated barlowite 2 was synthesized33 by mixing CuF2 (BTC, 99.5%), LiBr (Alfa, 99%), and 15 mL DI H2O in a 23 mL autoclave, which was heated over 3 h to 175 °C and held for 72 h, then cooled to 80 °C over 24 h. It was held at 80 °C for 24 h before being cooled to room temperature over 12 h. Deuterated barlowite 2 was prepared by combining a stoichiometric mixture of CuF2 (6 mmol) and LiBr (10.5 mmol) with 15 mL D2O in a 23 mL autoclave, which was then heated to over 3 h to 175 °C and held for 72 h, then cooled to 80 °C over 48 h. It was held at 80 °C for 96 h before being cooled to room temperature over 24 h. Zn0.56 crystals were grown using 14 excess equivalents of ZnF2. Adding ZnF2 in excess of this resulted in phase separation of the products. CuF2 (1.8 mmol), ZnF2 (9 mmol; Alfa, 99%), and LiBr (21 mmol) were sealed in a 23 mL autoclave with 15 mL DI H2O. This was heated over 3 h to 215 °C and held for 72 h, then cooled to 80 °C over 48 h. It was held at 80 °C for 72 h before being cooled to room temperature over 24 h. Zn0.95 and herbertsmithite were synthesized using Cu2(OH)2CO3, NH4F, and ZnBr2 (BTC, 99.999%) or ZnCl2 (Alfa, 99.999%) in a 23 mL autoclave with 10 mL DI H2O or D2O. This was heated over 3 h to 210 °C and held for 24 h before being cooled to room temperature over 30 h15,33,50.
Synchrotron SCXRD experiments were conducted at NSF’s ChemMatCARS beamline 15-ID at the Advanced Photon Source (APS), Argonne National Laboratory, using a Bruker D8 diffractometer equipped with a PILATUS3 X CdTe 1M detector or a Bruker APEX II detector. Data sets were collected using a wavelength of 0.41328 Å. Additional data sets were collected at beamline 12.2.1 at the Advanced Light Source (ALS), Lawrence Berkeley National Laboratory, using a Bruker D85 diffractometer equipped with a Bruker PHOTON II detector and a wavelength of 0.7288 Å. The data were integrated and corrected for Lorentz and polarization effects using SAINT and corrected for absorption effects using SADABS63. The structures were solved using intrinsic phasing in APEX3 and refined using the SHELXTL and OLEX2 software64,65. Hydrogen atoms were inserted at positions of electron density near the oxygen atom and were refined with a fixed bond length, and an isotropic thermal parameter 1.5 times that of the attached oxygen atom. Thermal parameters for all other atoms were refined anisotropically.
Synchrotron PXRD data were collected at APS beamline 11-BM using wavelengths of 0.412728, 0.412702, and 0.457676 Å. Samples were measured in Kapton capillaries; crystalline samples were crushed into a powder. Rietveld refinements were performed using GSAS-II66. Atomic coordinates and isotropic atomic displacement parameters were refined for each atom; site occupancy was also refined for the interlayer site when appropriate. Hydrogen was excluded.
NPD data were collected using the BT-1 32 detector neutron powder diffractometer at the Center for Neutron Research (NCNR) at the National Institute of Standards and Technology (NIST). A Ge(311) monochromator with a 75∘ take-off angle, wavelength of 2.0775 Å, and in-pile collimation of 60′ was used. Data were collected from 1.3–166.3∘ 2Θ with a step size of 0.05∘. The samples were loaded in vanadium cans. Rietveld co-refinements of PXRD and NPD data were performed using GSAS-II. Atomic coordinates and isotropic atomic displacement parameters were refined for each atom, including deuterium; site occupancy was also refined for the interlayer site when appropriate.
DC magnetization and AC susceptibility measurements were performed on a Quantum Design Physical Properties Measurement System (PPMS) from T = 2–50 K in applied fields up to μ0H = 9 T. AC susceptibility was measured with a 1.5 Oe drive current at a frequency of 10,000 Hz. DC susceptibility was measured on a Quantum Design Magnetic Property Measurement System (MPMS) from T = 2–300 K in applied fields up to μ0H = 7 T. Heat capacity measurements were performed in the PPMS with a dilution refrigerator on either a pressed single pellet of powder mixed with Ag powder in a 1:2 mass ratio or on a single crystal affixed to a sapphire platform using Apiezon-N grease. Ag powder was measured separately, and its contribution was subtracted.
Elastic neutron scattering measurements were performed on aligned single crystals of deuterated barlowite 2, with a total mass of 72.8 mg (266 coaligned crystals) at beamline HB-1A, the Fixed-Incident-Energy Triple-Axis Spectrometer, at the High Flux Isotope Reactor (HFIR), Oak Ridge National Laboratory. The incident and final energies were fixed at 14.656 meV, with horizontal collimation of 40′–40′–sample–80′–open, and a liquid helium cryostat was used to reach the base temperature of T = 1.6 K. Additional measurements were taken at the Spin Polarized Inelastic Neutron Spectrometer (SPINS) and the BT-7 Double Focusing Thermal Triple-Axis Spectrometer67 at the NCNR with a total sample mass of 226.7 mg (1115 coaligned crystals). For SPINS, the incident and final energies were fixed at 5 meV, with horizontal collimation of guide–open–sample–80′–open. For BT-7, the incident and final energies were fixed at 14.7 meV, with horizontal collimation of open–80′–sample–80′–120′. Base temperatures of T = 4 K (for one experiment at SPINS) and T = 2.7 K (BT-7 and another experiment at SPINS) were achieved using closed cycle refrigerators. The sample mosaic was 3.00∘–3.33∘ (FWHM) for all experiments, depending on the orientation. More details of the magnetic model analysis can be found in the Supplementary Material68,69,70,71,72,73.
We employ the standard DMRG method45 to investigate the ground state properties of the S = \(\frac{1}{2}\) AF \(J-J^{\prime}\) Heisenberg model on the kagome lattice. We take the lattice geometry to be cylindrical and lattice spacing to be unity. The boundary condition of the cylinder is periodic around the cylinder but open along the cylinder. We focus on cylinders of width Ly = 4, i.e., 4 unit cells or 8 sites around the cylinder. We keep around m = 4000 states in each DMRG block with a typical truncation error ϵ ≈ 10−6 and perform > 16 sweeps, which leads to excellent convergence of our results.
Data availability
The X-ray and neutron crystallographic coordinates for structures reported in this study have been deposited at the Cambridge Crystallographic Data Centre (CCDC), under deposition numbers 1898751–4, 1898756, 1899242–3, 1899250, 1899252, 1899365, 1899367, 1899369, 1899370, and 1922923. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif. Raw data were generated at the APS (beamlines 15-ID and 11-BM) and ALS synchrotron radiation facilities (beamline 12.2.1), as well as the HFIR (beamline HB-1A) and NIST Center for Neutron Research neutron sources (beamlines BT-1, BT-7, and SPINS). Data supporting the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The magnetic structure refinement code is available from the corresponding authors upon reasonable request.
Change history
12 February 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41535-020-0230-8
12 February 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41535-020-0249-x
References
Sachdev, S. Kagome- and triangular-lattice Heisenberg antiferromagnets: Ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys. Rev. B 45, 12377 (1992).
Ran, Y., Hermele, M., Lee, P. A. & Wen, X.-G. Projected-wave-function study of the spin-\(\frac{1}{2}\) Heisenberg model on the kagome Lattice. Phys. Rev. Lett. 98, 117205 (2007).
Hermele, M., Ran, Y., Lee, P. A. & Wen, X.-G. Properties of an algebraic spin liquid on the kagome lattice. Phys. Rev. B 77, 224413 (2008).
Jiang, H. C., Weng, Z. Y. & Sheng, D. N. Density matrix renormalization group numerical study of the kagome antiferromagnet. Phys. Rev. Lett. 101, 117203 (2008).
Yan, S., Huse, D. A. & White, S. R. Spin-liquid ground state of the \(S=\frac{1}{2}\) kagome Heisenberg antiferromagnet. Science 332, 1173–1176 (2011).
Depenbrock, S., McCulloch, I. P. & Schollwöck, U. Nature of the spin-liquid ground state of the \(S=\frac{1}{2}\) Heisenberg model on the kagome lattice. Phys. Rev. Lett. 109, 067201 (2012).
Jiang, H.-C., Wang, Z. & Balents, L. Identifying topological order by entanglement entropy. Nat. Phys. 8, 902–905 (2012).
Hao, Z. & Tchernyshyov, O. Spin-\(\frac{1}{2}\) Heisenberg antiferromagnet on the kagome lattice: Z2 spin liquid with fermionic spinons. Phys. Rev. B 87, 214404 (2013).
He, Y.-C., Zaletel, M. P., Oshikawa, M. & Pollmann, F. Signatures of Dirac cones in a DMRG study of the kagome Heisenberg model. Phys. Rev. X 7, 031020 (2017).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Norman, M. R. Colloquium: herbertsmithite and the search for the quantum spin liquid. Rev. Mod. Phys. 88, 041002 (2016).
Mendels, P. & Bert, F. Quantum kagome frustrated antiferromagnets: one route to quantum spin liquids. C. R. Phys. 17, 455–470 (2016).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Braithwaite, R. S. W., Mereiter, K., Paar, W. H. & Clark, A. M. Herbertsmithite, Cu3Zn(OH)6Cl2, a new species, and the definition of paratacamite. Mineral. Mag. 68, 527–539 (2004).
Shores, M. P., Nytko, E. A., Bartlett, B. M. & Nocera, D. G. A structurally perfect \(S=\frac{1}{2}\) kagome antiferromagnet. J. Am. Chem. Soc. 127, 13462–13463 (2005).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Fu, M., Imai, T., Han, T.-H. & Lee, Y. S. Evidence for a gapped spin-liquid ground gtate in a kagome Heisenberg antiferromagnet. Science 350, 655–658 (2015).
Zhu, W., Gong, S. S. & Sheng, D. N. Chiral and critical spin liquids in a spin-\(\frac{1}{2}\) kagome antiferromagnet. Phys. Rev. B 92, 014424 (2015).
Mei, J.-W., Chen, J.-Y., He, H. & Wen, X.-G. Gapped spin liquid with Z2 topological order for the kagome Heisenberg model. Phys. Rev. B 95, 235107 (2017).
Liao, H. J. et al. Gapless spin-liquid ground state in the S = \(\frac{1}{2}\) kagome antiferromagnet. Phys. Rev. Lett. 118, 137202 (2017).
Hastings, M. B. Dirac structure, RVB, and Goldstone modes in the kagome antiferromagnet. Phys. Rev. B 63, 014413 (2000).
Syromyatnikov, A. V. & Maleyev, S. V. Hidden long-range order in kagome Heisenberg antiferromagnets. Phys. Rev. B 66, 132408 (2002).
Nikolic, P. & Senthil, T. Physics of low-energy singlet states of the kagome lattice quantum Heisenberg antiferromagnet. Phys. Rev. B 68, 214415 (2003).
Singh, R. R. P. & Huse, D. A. Ground state of the spin-\(\frac{1}{2}\) kagome-lattice Heisenberg antiferromagnet. Phys. Rev. B 76, 180407(R) (2007).
Kim, J.-H. et al. External magnetic field effects on a distorted kagome antiferromagnet. Phys. Rev. Lett. 101, 107201 (2008).
Yoshida, H. et al. Orbital switching in a frustrated magnet. Nat. Commun. 3, 860 (2012).
Freedman, D. E. et al. Site specific x-ray anomalous dispersion of the geometrically frustrated kagome magnet, herbertsmithite, ZnCu3(OH)6Cl2. J. Am. Chem. Soc. 132, 16185–16190 (2010).
Han, T.-H. et al. Correlated impurities and intrinsic spin-liquid physics in the kagome material herbertsmithite. Phys. Rev. B 94, 060409(R) (2016).
Elliott, P., Cooper, M. A. & Pring, A. Barlowite, Cu4(OH)6FBr, a new mineral isotructural with claringbullite: description and crystal structure. Mineral. Mag. 78, 1755–1762 (2014).
Han, T.-H., Singleton, J. & Schlueter, J. A. Barlowite: A spin-\(\frac{1}{2}\) antiferromagnet with a geometrically perfect kagome motif. Phys. Rev. Lett. 113, 227203 (2014).
Jeschke, H. O. et al. Barlowite as a canted antiferromagnet: theory and experiment. Phys. Rev. B 92, 094417 (2015).
Han, T.-H., Isaacs, E. D., Schlueter, J. A. & Singleton, J. Anisotropy: spin order and magnetization of single-crystalline Cu4(OH)6FBr barlowite. Phys. Rev. B 93, 214416 (2016).
Smaha, R. W., He, W., Sheckelton, J. P., Wen, J. & Lee, Y. S. Synthesis-dependent properties of barlowite and Zn-substituted barlowite. J. Solid State Chem. 268, 123–129 (2018).
Feng, Z. et al. Effect of Zn doping on the antiferromagnetism in kagome Cu4−xZnx(OH)6FBr. Phys. Rev. B 98, 155127 (2018).
Tustain, K., Nilsen, G. J., Ritter, C., daSilva, I. & Clark, L. Nuclear and magnetic structures of the frustrated quantum antiferromagnet barlowite, Cu4(OH)6FBr. Phys. Rev. Mater. 2, 111405(R) (2018).
Liu, Z., Zou, X., Mei, J.-W. & Liu, F. Selectively doping barlowite for quantum spin liquid: a first-principles study. Phys. Rev. B 92, 220102(R) (2015).
Guterding, D., Valentí, R. & Jeschke, H. O. Reduction of magnetic interlayer coupling in barlowite through isoelectronic substitution. Phys. Rev. B 94, 125136 (2016).
Feng, Z. et al. Gapped spin-\(\frac{1}{2}\) spinon excitations in a new kagome quantum spin liquid compound Cu3Zn(OH)6FBr. Chinese Phys. Lett. 34, 077502 (2017).
Wei, Y. et al. Evidence for a Z2 topological ordered quantum spin liquid in a kagome-lattice antiferromagnet. Preprint at http://arxiv.org/abs/1710.02991 (2017).
Pasco, C. M. et al. Single crystal growth of Cu4(OH)6BrF and universal behavior in quantum spin liquid candidates synthetic barlowite and herbertsmithite. Phys. Rev. Mater 2, 044406 (2018).
Henderson, A. et al. Order-disorder transition in the \(S=\frac{1}{2}\) kagome antiferromagnets claringbullite and barlowite. Chem. Commun. 55, 11587–11590 (2019).
Warren, B. X-Ray Diffraction (Dover Publications, 1990).
Reisinger, S. A., Tang, C. C., Thompson, S. P., Morrison, F. D. & Lightfoot, P. Structural phase transition in the \(S=\frac{1}{2}\) kagome system Cs2ZrCu3F12 and a comparison to the valence-bond-solid phase in Rb2SnCu3F12. Chem. Mater. 23, 4234–4240 (2011).
Kato, H., Kato, M., Yoshimura, K. & Kosuge, K. Structural and magnetic phase transitions of AV6O11 (A = Na, Sr, and Pb). J. Phys. Condens. Matter 13, 9311–9333 (2001).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Jeschke, H. O., Salvat-Pujol, F. & Valentí, R. First-principles determination of Heisenberg Hamiltonian parameters for the spin-\(\frac{1}{2}\) kagome antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. B 88, 075106 (2013).
Han, T.-H., Chu, S. & Lee, Y. S. Refining the spin Hamiltonian in the spin-\(\frac{1}{2}\) kagome lattice antiferromagnet ZnCu3(OH)6Cl2 using single crystals. Phys. Rev. Lett. 108, 157202 (2012).
Wang, J., Zhou, Z., Zhang, W., Garoni, T. M. & Deng, Y. Bond and site percolation in three dimensions. Phys. Rev. E 87, 052107 (2013).
Bert, F. et al. Low temperature magnetization of the \(S=\frac{1}{2}\) kagome antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. B 76, 132411 (2007).
Han, T. H. et al. Synthesis and characterization of single crystals of the spin- \(S=\frac{1}{2}\) kagome-lattice antiferromagnets ZnxCu4−x(OH)6Cl2. Phys. Rev. B 83, 100402(R) (2011).
Helton, J. S. et al. Spin dynamics of the spin-\(\frac{1}{2}\) kagome lattice antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. Lett. 98, 107204 (2007).
Matan, K. et al. Pinwheel VBS state and triplet excitations in the two-dimensional deformed kagome lattice. Nat. Phys. 6, 865–869 (2010).
Messio, L., Cépas, O. & Lhuillier, C. Schwinger-boson approach to the kagome antiferromagnet with Dzyaloshinskii-Moriya interactions: Phase diagram and dynamical structure factors. Phys. Rev. B 81, 064428 (2010).
Huh, Y., Fritz, L. & Sachdev, S. Quantum criticality of the kagome antiferromagnet with Dzyaloshinskii-Moriya interactions. Phys. Rev. B 81, 144432 (2010).
Suttner, R., Platt, C., Reuther, J. & Thomale, R. Renormalization group analysis of competing quantum phases in the J1–J2 Heisenberg model on the kagome lattice. Phys. Rev. B 89, 020408(R) (2014).
Fejer, E. E., Clark, A. M., Couper, A. G. & Elliott, C. J. Claringbullite, a new hydrated copper chloride. Mineral. Mag. 41, 433–436 (1977).
Burns, P. C., Cooper, M. A. & Hawthorne, F. C. Claringbullite: a Cu2+ oxysalt with Cu2+ in trigonal-prismatic coordination. Can. Mineral. 33, 633–639 (1995).
Feng, Z. et al. From claringbullite to a new spin liquid candidate Cu3Zn(OH)6FCl. Chinese Phys. Lett. 36, 017502 (2019).
Jambor, J. L., Dutrizac, J. E., Roberts, A. C., Grice, J. D. & Szymanski, J. T. Clinoatacamite, a new polymorph of Cu2(OH)3Cl, and its relationship to paratacamite and “Anarakite”. Can. Mineral. 34, 61–72 (1996).
Malcherek, T., Mihailova, B. & Welch, M. D. Structural phase transitions of clinoatacamite and the dynamic Jahn-Teller effect. Phys. Chem. Miner. 44, 307–321 (2017).
Wills, A. S. & Henry, J.-Y. On the crystal and magnetic ordering structures of clinoatacamite, γ-Cu2(OD)3Cl, a proposed valence bond solid. J. Phys. Condens. Matter 20, 472206 (2008).
Clark, B. K., Kinder, J. M., Neuscamman, E., Chan, G. K.-L. & Lawler, M. J. Striped spin liquid crystal ground state instability of kagome antiferromagnets. Phys. Rev. Lett. 111, 187205 (2013).
Bruker AXS Software Inc. (Madison, 2016).
Sheldrick, G. M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 71, 3–8 (2015).
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: a complete structure solution, refinement, and analysis program. J. Appl. Crystallogr. 42, 339–341 (2009).
Toby, B. H. & Von Dreele, R. B. GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 46, 544–549 (2013).
Lynn, J. W. et al. Double focusing thermal triple axis spectrometer at the NCNR. J. Res. NIST 117, 61–79 (2012).
Abel, E. T. et al. X-ray scattering study of the spin-Peierls transition and soft phonon behavior in TiOCl. Phys. Rev. B 76, 214304 (2007).
Shirane, G., Shapiro, S. M. & Tranquada, J. M. Neutron Scattering with a Triple-Axis Spectrometer: Basic Techniques (Cambridge University Press, 2002).
Aroyo, M. I., Kirov, A., Capillas, C., Perez-Mato, J. M. & Wondratschek, H. Bilbao crystallographic server: II. representations of crystallographic point groups and space groups. Acta Crystallogr. A 62, 115–128 (2006).
Aroyo, M. I. et al. Bilbao crystallographic server: I. databases and crystallographic computing programs. Z. Krist.-Cryst. Mater. 221, 15–27 (2006).
Aroyo, M. I. et al. Crystallography online: Bilbao crystallographic server. Bulg. Chem. Commun. 43, 183–197 (2011).
Perez-Mato, J. M. et al. Symmetry-based computational tools for magnetic crystallography. Annu. Rev. Mater. Res. 45, 217–248 (2015).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
The work at Stanford and SLAC was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under contract no. DE-AC02-76SF00515; this includes the synthesis, physical property measurements, neutron scattering, X-ray scattering, and numerical simulations. A portion of this research used resources at the HFIR, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. We acknowledge the support of the National Institute of Standards and Technology, U. S. Department of Commerce, in providing the neutron research facilities used in this work. This research used resources of the ALS, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. Use of the APS, an Office of Science User Facility operated for the U.S. DOE Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under contract no. DE-AC02-06CH11357. NSF’s ChemMatCARS Sector 15 is supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant number NSF/CHE-1834750. Use of the PILATUS3 X CdTe 1M detector is supported by the National Science Foundation under grant number NSF/DMR-1531283. Part of this work was performed at the Stanford Nano Shared Facilities, supported by the NSF under award ECCS-1542152. R.W.S. was supported by the Department of Defense through the NDSEG Fellowship Program and by an NSF Graduate Research Fellowship (DGE-1656518). We thank S. Lapidus for assistance at APS beamline 11-BM; C.M. Brown for assistance at NCNR beamline BT-1; I.R. Fisher for use of the MPMS and dilution refrigerator; A.T. Hristov for help with the dilution refrigerator; and S. Raghu, T. Senthil, and G. Chen for helpful discussion. The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology.
Author information
Authors and Affiliations
Contributions
R.W.S. and Y.S.L. conceived the study, interpreted the data, and wrote the manuscript with contributions and comments from all authors. R.W.S. synthesized barlowite 2 and all Zn-substituted barlowite samples; performed and analyzed X-ray and neutron diffraction measurements; and performed and analyzed magnetic susceptibility and heat capacity measurements. W.H. synthesized barlowite 1 and performed and analyzed neutron scattering measurements. J.M.J., C.J.T. and J.W. aided at beamtimes and with data analysis. Y.-F.J. and H.C.J. performed numerical calculations. J.P.S. synthesized herbertsmithite. S.G.W., Y.-S.C., S.J.T., A.A.A., Y.Z., G.X. and J.W.L. aided at beamtimes.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Smaha, R.W., He, W., Jiang, J.M. et al. Materializing rival ground states in the barlowite family of kagome magnets: quantum spin liquid, spin ordered, and valence bond crystal states. npj Quantum Mater. 5, 23 (2020). https://doi.org/10.1038/s41535-020-0222-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0222-8
This article is cited by
-
Emergence of the spin polarized domains in the kagome lattice Heisenberg antiferromagnet Zn-barlowite (Zn0.95Cu0.05)Cu3(OD)6FBr
npj Quantum Materials (2022)
-
Emergence of spin singlets with inhomogeneous gaps in the kagome lattice Heisenberg antiferromagnets Zn-barlowite and herbertsmithite
Nature Physics (2021)
-
From magnetic order to quantum disorder in the Zn-barlowite series of S = 1/2 kagomé antiferromagnets
npj Quantum Materials (2020)