Abstract
Violation of time reversal and spatial inversion symmetries has profound consequences for elementary particles and cosmology. Spontaneous breaking of these symmetries at phase transitions gives rise to unconventional physical phenomena in condensed matter systems, such as ferroelectricity induced by magnetic spirals, electromagnons, non-reciprocal propagation of light and spin waves, and the linear magnetoelectric (ME) effect—the electric polarization proportional to the applied magnetic field and the magnetization induced by the electric field. Here, we report the experimental study of the holmium-doped langasite, HoxLa3−xGa5SiO14, showing a puzzling combination of linear and highly non-linear ME responses in the disordered paramagnetic state: its electric polarization grows linearly with the magnetic field but oscillates many times upon rotation of the magnetic field vector. We propose a simple phenomenological Hamiltonian describing this unusual behavior and derive it microscopically using the coupling of magnetic multipoles of the rare-earth ions to the electric field.
Similar content being viewed by others
Introduction
Novel materials and physical effects are essential for the continuing progress in nanoelectronics1. The coupling between electric and magnetic dipoles in magnetoelectric (ME) and multiferroic materials enables electric control of magnetism that can significantly reduce power consumption of magnetic memory and data processing devices2,3,4,5,6.
The linear ME effect7,8,9 occurs in centrosymmetric crystals, such as Cr2O310 and LiCoPO411, in which both time reversal and inversion symmetries are spontaneously broken by an antiferromagnetic spin ordering inducing toroidal, monopole, and other unconventional multipole moments12. This effect allows for control of antiferromagnetic domains and gives rise to unidirectional light transmission at THz frequencies associated with electromagnons13,14,15.
However, the linear ME effect in centrosymmetric crystals requires a perfect match between magnetic and lattice structures, which narrows the pool of ME materials substantially. Symmetry requirements are less stringent for magnets with non-centrosymmetric crystal lattices, such as boracites16, copper metaborates17, and the skyrmion material, Cu2OSeO318, in which diverse magnetic orders exhibit ME behavior.
A bi-linear ME effect—electric polarization proportional to the second power of the applied magnetic field—does not even require time-reversal symmetry breaking and can occur in the paramagnetic state of non-centrosymmetric magnets through a variety of miscroscopic mechanisms19,20. This higher-order effect is by no means weak: the magnetically induced electric polarization in the recently studied holmium hexaborate is much higher than the polarization of linear MEs at comparable magnetic fields21.
The Ho-doped langasite studied in this paper does not seem to fit into this classification of ME effects. Langasite, La3Ga5SiO14, and related compounds have been synthesized as early as the 1980s22,23 and actively studied since then24 for their interesting non-linear optical, elastic and piezoelectric25,26 properties and applications in acousto- and electro-optics27,28. The non-centrosymmetric crystallographic space group P321 of langasites allows for optical rotation and piezoelectricity, but not for spontaneous electric polarization due to the presence of orthogonal threefold and twofold symmetry axes. The study of ME properties was focused on Fe-substituted langasites showing non-collinear periodically modulated orders of Fe spins29. The interplay between magnetic frustration, structural and spin chiralities gives rise to a rich variety of multiferroic behaviors30,31.
The Ho-doped langasite does not order down to lowest temperatures. Yet, its magnetically induced electric polarization oscillates 6 times when the direction of the magnetic field rotates through 360∘ in the ab-plane, which is indicative of a highly non-linear ME response proportional to (at least) the sixth power of the magnetic field. On the other hand, the magnitude of the induced polarization grows linearly with the applied field, which seems to be at odds with the absence of any magnetic ordering in this material. This ME behavior is very different from that of classical MEs, such as Cr2O3. We show that it can be understood on the basis of langasite symmetry and a hierarchy of energy scales in the spectrum of the magnetic Ho ion.
Results
Experiment
The samples used in this work are diluted rare-earth langasites, HoxLa3−xGa5SiO14, with x = 0.043 ± 0.005. The crystal structure of R3Ga5SiO14 langasites32,33 is shown in Fig. 1a. The rare-earth sites, R, have a rather low C2 symmetry with the rotation axis along the a-axis of the crystal, allowing for electric dipole moments on R-sites, which in the case of magnetic Ho ions can depend on an applied magnetic field.
a The distorted Kagome lattice of the rare-earth ions in R3Ga5SiO14. About 1.5% of the rare-earth sites (orange) are occupied by the holmium ions. The unit cell is shown by thin solid lines. b Experimental and theoretical magnetization curves of HoxLa3−xGa5SiO14 (x = 0.043) in external magnetic fields parallel to three crystallographic axes and at T = 5 K. Symbols—experiment, solid lines—model accounting for a ground Ho3+ quasidoublet and a Van-Vleck contribution of excited crystal-field states. The inset shows the local magnetic moments of Ho-ions in the saturation regime.
The field-dependence of magnetization (Fig. 1b) shows saturation at fields ~1 T at low temperatures, which suggests that the magnetism of Ho3+ (5I8) ions in langasites is dominated by the two lowest-energy levels split by the crystal field from other states of the J = 8 multiplet. The level splitting in this so-called non-Kramers doublet, Δ, is estimated to be 3.1 K. As discussed below, based on symmetry arguments and magnetization fits, the Ising-type magnetic moments of Ho-ions are oriented perpendicular to the local symmetry axis, i.e., in the XiYi plane, forming an angle γ ≈ 30∘ with the crystallographic c-axis (Fig. 1b). γ is the only free magnetic anisotropy parameter in our model that reproduces well the field dependence of the magnetization along the b* and c-axes (see Fig. 1a) but underestimates the magnetization for H∥a, which is indicative of deviations of the magnetic moments from the XiYi-plane (see discussion below).
Figure 2 shows the angular dependence of the electric polarization along the c-axis, Pc, for the magnetic field vector, H, rotated in the ac- and ab-planes. The complex angular dependence is indicative of a high-order ME effect resulting from the C3 symmetry of langasite. Although the expansion of the magnetically induced electric dipole of the Ho-ion in powers of H begins with terms ∝ H2, the bilinear ME effect is cancelled in the sum over the dipole moments of the Ho dopants in the three La sublattices.
a Pc vs the polar angle θ between the applied magnetic field, H, and the c-axis, for H rotated in the ac-plane at several temperatures. b Pc vs the azimuthal angle φ for H rotated in the ab-plane. The modulation with the 60∘ period is indicative of a high-order ME effect (see Eq. (2)). Experimental data are shown with symbols, and solid lines are calculated within the model described in the text.
The lowest-order phenomenological expression for Pc allowed by C3 and C2 symmetries is
where we use the Cartesian coordinates with \(\hat{{\bf{x}}}=\hat{{\bf{a}}}\), \(\hat{{\bf{y}}}={\hat{{\bf{b}}}}^{* }\), \(\hat{{\bf{z}}}=\hat{{\bf{c}}}\) and a4(T) is a material constant. Fourth-order ME effect in crystals with trigonal crystal symmetry was discussed earlier34,35,36. Equation (1) implies that \({P}_{z}\propto {\sin }^{2}\theta \sin 2\theta \cos 3\varphi\), where θ and φ are, respectively, the polar and azimuthal angles describing the magnetic field direction. This angular dependence is in good agreement with the results of experimental measurements at high temperatures shown in Fig. 2a, whereas at low temperatures the experimental θ-dependence becomes more complex, indicating substantial higher-order contributions to the ME effect.
The fourth-order ME effect described by Eq. (1) gives zero electric polarization for a magnetic field in the basal ab plane. However, the experimentally measured electric polarization shown in Fig. 2b is of the same order as that for out-of-plane fields. The electric polarization shows a periodic dependence on the azimuthal angle, φ, with the period of 60∘ apparently resulting from a sixth-order ME effect. The lowest-order expression for the electric polarization induced by an in-plane magnetic field is, indeed, of sixth order in H:
The sixth-order ME response has not been discussed earlier. The right-hand side of Eq. (2), found using symmetry arguments34,35,36, is the lowest-order polynomial of Hx and Hy that transforms as Pz. The saw-tooth shape of the angular dependence of the polarization at low temperatures (Fig. 2b) indicates contributions of ME effects of yet higher orders.
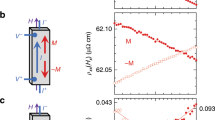
Equations (1) and (2) imply that the electric polarization is proportional to the 4th or 6th power of the applied magnetic field, depending on the orientation of H. Instead, at low temperatures we obseve a nearly linear dependence of Pz for any field direction (see Fig. 3). Importantly, phenomenological Eqs. (1) and (2) only hold for weak magnetic fields, ∣μ0H∣ ≪ max(Δ, kBT), μ0 being the saturated magnetic moment of a Ho3+ ion (these equations are obtained in Methods by expansion in powers of H). At low temperatures, their validity is limited to fields ≲ 1 T (see Fig. 1b). The saturation of the Ho magnetic moment at higher magnetic fields gives rise to higher-order harmonics in the observed angular dependence of the electric polarization.
Counterintuitively, the onset of a more complex θ- and φ-dependence correlates with the crossover to a linear dependence of Pz on the magnitude of the magnetic field (Fig. 3). In what follows we discuss the theory behind this unusual ME effect.
a Electric polarization for magnetic fields in the ac-plane with θ = 45∘ (see also Fig. 2a). Symbols are experimental data, dashed lines are results of theoretical calculations. The inset shows temperature dependence of the strength of the 4th-order magnetoelectric response, a4 in Eq. (1), obtained from the low-field slopes. Symbols are experimental data; the line is the T−3 fit. b Magnetic field dependence of the electric polarization, Pc, for applied magnetic fields rotated in the ab plane through 15∘ from the b*-axis (see also Fig. 2b). The inset shows temperature dependence of the strength of the 6th-order magnetoelectric response, a6 in Eq. (2), obtained from the low-field slopes. Symbols are experimental data; the line is the T−5 fit.
Theory
In the absence of inversion symmetry, the rare-earth ions interact with the electric field, E, through an effective dipole moment operator, \(\hat{{\bf{d}}}\), which in the subspace of the ground-state multiplet can be expressed in terms of the quadrupole and higher-order magnetic multipole moments of the ions37. The spectrum of the low-energy states depends then on both electric and magnetic fields, which gives rise to a ME response of the rare-earth ions. The description of the ME effect in Ho-langasite can be simplified by projecting the Hamiltonian describing the ME behavior of the ground-state multiplet on the subspace of the two states, \(\left|A\right\rangle\) and \(\left|B\right\rangle\), forming the non-Kramers doublet (see “Methods”).
Alternatively, the Hamiltonian describing the ME coupling of the non-Kramers doublet can be directly deduced from symmetry considerations. Within the unit cell of Ho-langasite, there are three equivalent rare-earth positions with local C2 symmetry axes along the \({\hat{Z}}_{i}\) (i = 1, 2, 3) directions related by 120∘-rotations around the crystallographic c axis. At site 1, \({\hat{Z}}_{1}\parallel a\), \({\hat{Y}}_{1}\parallel c\) (along the C3-symmetry axis) and \({\hat{X}}_{1}=[{\hat{Y}}_{1}\times {\hat{Z}}_{1}]\). In the local coordinate frame, the ME Hamiltonian is,
(the index i = 1, 2, 3 labeling the rare-earth ion is omitted for simplicity). Equation (3) is a general symmetry-allowed expression provided one of the states forming the doublet is even and another is odd under \({C}_{2}={2}_{{Z}_{i}}\), in which case the magnetic moment of the doublet lies in the XiYi plane and thus can have a nonzero component along the crystallographic c axis. If both states would transform in the same way under \({2}_{{Z}_{i}}\), the magnetic moment would be parallel to the Zi axis and the magnetic moments of all Ho ions would lie in the ab plane, in disagreement with the experiment.
The Y-component of the polarization (P∥c) measured in our experiment, results from the third term in Eq. (3). For EX = EZ = 0 and EY = Ec, the total effective Hamiltonian in the subspace spanned by the \(\left|A\right\rangle\) and \(\left|B\right\rangle\) states is:
where (σx, σy, σz) are Pauli matrices, Δ is the crystal-field splitting, μ = (μX, μY, 0) and dY are, respectively, the (transitional) magnetic and electric dipole moments of the Ho3+ ion. The form of \({\hat{H}}_{{\rm{e}}ff}\) is constrained by 2Z and time-reversal symmetries of the Ho ions. In addition, 3c symmetry implies that the (real) coefficients, dY, μX, μY and gYZ are the same for all Ho-sublattices.
The free energy of the doublet, fi (i = 1, 2, 3), can now be easily calculated and the magnetically induced electric polarization is given by
where nHo is the density of Ho ions and Mi is related to the average magnetic moment of the i-th Ho ion by 〈μi〉 = (μX, μY, 0)Mi and equals
where +ϵi and −ϵi are energies of the two states forming the doublet, \(({\boldsymbol{\mu }}\cdot {{\bf{H}}}_{i})={\mu }_{X}{H}_{{X}_{i}}+{\mu }_{Y}{H}_{{Y}_{i}}\) and β = 1/kBT. In zero applied electric field, \({\epsilon }_{i}=\sqrt{{({\boldsymbol{\mu }}\cdot {{\bf{H}}}_{i})}^{2}+{(\Delta /2)}^{2}}\) (for details see the Methods section and refs. 38,39,40,41). The resulting magnetic field-dependence of the electric polarization (dashed lines in Figs. 2 and 3) is in reasonable agreement with experimental data.
The largest discrepancy between theory and experiment is found in the angular dependence of the electric polarization shown in Fig. 2. The main reason for this deviation is the intrinsic disorder in the langasite crystal structure (Fig. 1). The four positions in the local surrounding of rare-earth ions are randomly occupied by two Si and two Ga ions24,32 resulting in six inequivalent Ho ions in each sublattice. The concomitant lattice distortions affect magnetic anisotropy and ME interactions of the ions. Importantly, our simplified model based on average symmetry of rare-earth ions captures the basic physics of the ME response of Ho-langasite.
Discussion
Figure 3 demonstrates that the electric polarization is a linear function of the applied field strength in the broad range of temperatures and external magnetic fields. The region of linear effect agrees well with the regime of saturated magnetic moments shown in Fig. 1b. This can be understood by noting that Eq. (5) can be obtained from the ME coupling, \(-{g}_{YZ}{E}_{c}{H}_{{Z}_{i}}{M}_{i}\), on the i-th Ho sublattice. At low temperatures, βϵi ≫ 1, Mi grows with the applied magnetic field and approaches unity at rather weak fields, ∣μ0H∣ ~ Δ, above which the magnetic moment saturates and the ME coupling becomes linear.
Importantly, the ME coupling in Eq. (3) originates from the admixture of higher-energy excited states from the J = 8 multiplet to \(\left|A\right\rangle\) and \(\left|B\right\rangle\) in the presence of electric and magnetic fields (see Methods). The linear ME effect is a consequence of a relatively large energy separation, W, of the non-Kramers doublet from the higher-energy states: it is observed for Δ ≪ ∣μ0H∣ ≪ W, when the dipole magnetic moment of the doublet is saturated while the admixture of higher-energy states remains small. Rear-earth ions with Kramers doublets can also show linear ME response, which makes the whole series of the rare-earth dopands potentially interesting for studies of this unusual phenomenon.
There is an additional ME coupling that results from the matrix elements of the electric and magnetic dipole operators between the \(\left|A\right\rangle\) and \(\left|B\right\rangle\) states in Eq. (4) and does not involve high-energy excited states. This coupling, however, is proportional to second and higher powers of the electric field and does not contribute to the magnetically induced electric polarization measured in zero applied electric field, which can be traced back to the fact that the electric dipole is even and magnetic dipole is odd under time reversal.
Next we explain how the linear dependence of Pc on the magnetic field strength can be compatible with the complex dependence on the direction of the field (see “Methods” for more details). The six-fold periodicity of the polarization with the azimuthal angle is related to the presence of three rare-earth sublattices. Each sublattice separately gives rise to oscillations with the period of 180∘ (see Eq. (17)), since the Ising-like Ho magnetic moment changes sign as the magnetic field rotates in the ab-plane. Similar twofold periodicity is observed in the ME Co4Nb2O9 with Heisenberg spins, where the Néel vector describing an antiferromagnetic ordering of Co spins rotates together with the magnetic field vector42. In addition, the ME effect in Ho-langasite is a sum of the responses of the three kinds of Ho positions with magnetic moments rotated through 120∘ around the c axis, which gives rise to oscillations with the period of 60∘.
Ho-langasite can show the inverse effect—an electrically induced magnetization ∝ Ec—even though the ME coupling is an even function of H. The sensitivity to the magnetic field sign, important for applications of ME materials, is recovered under a bias magnetic field. An additional, electrically induced magnetization changes sign under the electric field reversal. If the bias field is strong enough to saturate Ho magnetic moments, the inverse ME effect is linear (see “Methods” for more details).
We have shown that the magnetic and ME properties of Ho-langasite may be understood taking into account the two lowest crystal-field levels of Ho3+ and the interplay of the local and global symmetries. Our theory reconciles a complex oscillating dependence of the polarization on the magnetic field direction with a linear dependence on its magnitude. The electric polarization is enabled by the absence of inversion symmetry at the local Ho positions. In weak magnetic fields, when the Zeeman energy is small compared to the energy splitting in the non-Kramers doublet, the polarization is described by Eqs. (1), (2) and is highly non-linear in H. It becomes linear in the strong-field limit, when the induced magnetic moment of Ho ions saturates, but it remains a complicated function of the magnetic field direction.
Importantly, the doping of non-centrosymmetric materials by magnetic rare-earth ions at low-symmetry positions provides a route to a linear ME response that does not require special magnetic orders and crystal lattices, as it occurs already in the paramagnetic state. Oscillatory dependence of magnetic and ME responses on the direction of the applied magnetic field is governed by crystal symmetry and is a generic property of such systems.
Methods
Experimental
Single crystals of doped holmium langasite HoxLa3−xGa5SiO14 were grown by the Czochralski technique. The crystals were proven to be right-handed single domain24,32. The handedness of langasites is likely a result of the growth procedure24. The orientation and crystallinity of the samples have been controlled using Laue-analysis. The actual concentration of holmium has been obtained using the total reflection X-ray fluorescence spectroscopy. The sample showed homogeneous polarization rotation of about 5∘ for the green light, which agrees with literature data43.
For the electric polarization experiments a plane-parallel plate with thickness d = 2.13 mm and area A = 106 mm2 has been cut with the flat surface perpendicular to the c-axis (c-cut). Silver paste electrodes were applied to two surfaces of the sample parallel to the ab-plane. The polarization was measured using an electrometer adapted to a Physical Property Measuring System, with magnetic fields of up to 14 T and temperatures down to 2 K. By changing the orientation of the sample in the cryostat, the direction of the magnetic field relative to the crystal axes was adjusted. The magnetization was measured using a commercial Vibrating Sample Magnetometer with magnetic fields up to 6 T. In these experiments, smaller samples from the same batch were used.
Microscopic theory of ME effect in Ho-langasite
The symmetry of the rare-earth environment in langasites is described by the point group C2. This cyclic group has two one-dimensional representations with respect to the rotation through an angle π around the twofold symmetry axis (local Zi-axis): the symmetric, A, and antisymmetric, B, representations. Ho3+ with an even number of f-electrons is a non-Kramers ion. The crystal field with C2 symmetry completely removes the degeneracy of the ground 5I8 multiplet that splits into 2J + 1 = 17 singlets with the wave functions transforming according to either A or B irreducible representations of the C2 group.
In the absence of inversion, the rare-earth ions interact with the electric field, E, through an effective dipole moment operator, \(\hat{{\bf{d}}}\), which in the space of the Ho3+ ground-state multiplet can be expressed in terms of the quadrupole and higher-order magnetic multipole moments of the ions37:
where \({\hat{Q}}_{\alpha \beta }=\frac{1}{2}[{\hat{J}}_{\alpha }{\hat{J}}_{\beta }+{\hat{J}}_{\beta }{\hat{J}}_{\alpha }-\frac{2}{3}J(J+1){\delta }_{\alpha \beta }]\) is the quadrupole moment operator, \(\hat{{\bf{J}}}=({\hat{J}}_{X},{\hat{J}}_{Y},{\hat{J}}_{Z})\) being the total angular momentum operator of the Ho3+ lowest-energy multiplet, a, b and c are phenomenological constants and the higher-order multipoles are omitted. Equation (7) is written in the local coordinate frame, (Xi, Yi, Zi), and the index i = 1, 2, 3 labeling the rare-earth ion is omitted for simplicity. The phases of the wave functions forming the ground-state multiplet can be chosen in such a way that the matrix elements of the electric dipole (even under time-reversal) are real, whereas the matrix elements of the magnetic dipole (odd under time-reversal) are all imaginary.
The ground state of the Ho3+ ion in the crystal-field potential, Vcf, is a quasi-doublet (two close-by singlets with the gap Δ ~ 2 cm−1) which are separated by the energy W ~ 30–50 cm−1 from the excited crystal-field states. The wave functions, \(\left|A\right\rangle\) and \(\left|B\right\rangle\), of the quasi-doublet can belong either to the same or to different representations. As discussed in the main text, the c-component of the magnetization measured in the experiment is nonzero only in the latter case.
The response of Ho3+ ions to the applied electric and magnetic fields is described by \(\hat{V}=-\hat{{\bf{d}}}\cdot {\bf{E}}+{\mu }_{{\rm{B}}}{g}_{{\rm{L}}}\hat{{\bf{J}}}\cdot {\bf{H}}\), where the first term describes the coupling of the effective dipole operator Eq. (7) to the electric field and the second term is the Zeeman coupling, μB and gL = 5/4 being, respectively, the Bohr magneton and the Lande factor. To describe the ME response of the Ho-langasite, we project the total Hamiltonian, \(\hat{H}=\hat{V}+{\hat{V}}_{{\rm{c}}f}\), on the quasi-doublet subspace:
where i, j = 1, 2 label the states of the non-Kramers doublet, \(\left|A\right\rangle\) and \(\left|B\right\rangle\), and the effect of the higher-energy states from the 5I8 multiplet (k = 3, 4, …, 17) is treated in the second order of perturbation theory assuming \(| \langle k| \hat{V}| i\rangle | \ll W\), and \({W}_{k}={E}_{k}-\frac{({E}_{1}\,+\,{E}_{2})}{2}\). We note that this approach can also be used to analyze the rare-earth contribution to magneto-elastic and optical properties.
The matrix elements of \(\hat{V}\) in the quasi-doublet subspace are constrained by C2 symmetry (cf. Eq. (4)):
where I is the 2 × 2 identity matrix, \({\bf{d}}\cdot {{\bf{E}}}_{i}=\langle A| \hat{{\bf{d}}}\cdot {{\bf{E}}}_{i}| B\rangle ={d}_{X}{E}_{{X}_{i}}+{d}_{Y}{E}_{{Y}_{i}}\) and \({\boldsymbol{\mu }}\cdot {{\bf{H}}}_{i}=-i{\mu }_{{\rm{B}}}{g}_{J}\langle A| \hat{{\bf{J}}}\cdot {{\bf{H}}}_{i}| B\rangle ={\mu }_{X}{H}_{{X}_{i}}+{\mu }_{Y}{H}_{{Y}_{i}}\). Due to the 3c symmetry of the langasite crystal, the real coefficients d0, dX, μX, etc. are the same for all Ho sites, i.e., are independent of i. The phases of the wavefunctions \(\left|A\right\rangle\) and \(\left|B\right\rangle\) are chosen such that the matrix elements of the time-even electric dipole operator involve real matrices, I and σx, whereas the time-odd magnetic dipole operator is proportional to σy with imaginary matrix elements.
In the last term of Eq. (8) we only leave the off-diagonal parts proportional to the product of the matrix elements of \(\hat{{\bf{d}}}\cdot {\bf{E}}\) and \({\mu }_{{\rm{B}}}{g}_{{\rm{L}}}\hat{{\bf{J}}}\cdot {\bf{H}}\) giving rise to the ME coupling,
(cf. Eq. (3)). Here, the coefficients gXY, gYX, etc. are real numbers. This interaction is invariant under C2 and time-reversal symmetries, and since it involves both the electric and magnetic dipole operators, the matrix elements of \({\hat{H}}_{{\rm{m}}e}\) in the quasi-doublet subspace are imaginary.
Adding all contributions to the effective two-level Hamiltonian and assuming \({E}_{{X}_{i}}={E}_{{Z}_{i}}=0\) and \({E}_{{Y}_{i}}={E}_{c}\) (i = 1, 2, 3), we obtain Eq. (4). The energies of the states forming the non-Kramers doublet at the i-th Ho3+ site, obtained by diagonalization of the Hamiltonian Equation (4), equal ±ϵi, where
The free energy is then given by
where nHo is the density of Ho ions and kB is the Boltzmann constant. The average magnetic moment measured at zero applied electric field is
where \(\beta =\frac{1}{{k}_{{\rm{B}}}T}\), μ0 is the magnetic moment of the non-Kramers doublet and mi is a unit vector defined by
The relation between the unit vectors in the hexagonal, Cartesian and the three local frames (see Fig. 1a) is:
On all three sites \({\hat{Y}}_{i}=(0,0,1)\) in the Cartesian coordinates, \({\hat{Z}}_{2,3}=(-\frac{1}{2},\pm\! \frac{\sqrt{3}}{2},0)\) and \({\hat{X}}_{2,3}=(\!\mp\! \frac{\sqrt{3}}{2},-\frac{1}{2},0)\).
The c-component of the electric polarization measured in our experiment is given by
Note that since the electric polarization is measured at zero applied electric field, dY that enters into the expression for the energy levels Eq. (11), drops out from the expression for Pc, in which \({\epsilon }_{i}=\sqrt{{({\boldsymbol{\mu }}\cdot {{\bf{H}}}_{i})}^{2}+{(\Delta /2)}^{2}}\). The energy splitting in the non-Kramers doublet by both electric and magnetic fields (see Eqs. (9) and (11)) does not result in the ME coupling linear in electric field, because the electric and magnetic dipoles transform with opposite signs under time reversal. The observed ME effect originates solely from the admixture of higher-energy states in applied electric and magnetic fields (the last term in Eq. ((8)). In addition, Ho ions carry a “built-in” electric dipole moment along the local Zi axis in the ab plane, which results from the first term in Eq. (9) and is independent of the magnetic field. These electric dipoles on three Ho sites are rotated through 120∘ around the c axis with respect to each other and give no net contribution to the electric polarization.
In the limit of strong fields and low temperatures, ∣μ ⋅ Hi∣ ≫ Δ, kBT, when the magnetic moment saturates, the electric polarization,
shows a complex saw-tooth dependence on the direction of the magnetic field in the ab plane (due to the sign-functions) and, at the same time, a simple linear dependence on the strength of the magnetic field, in agreement with our experimental observations.
In the opposite limit of weak fields and high temperatures, kBT ≫ ∣μ0H∣, Δ,
where H is the magnitude of the magnetic field and \(\gamma =\arccos ({\mu }_{Y}/{\mu }_{0})\), which agrees with Eq. (1) obtained by symmetry and gives a4(T) ∝ T−3. At zero temperature, \({({k}_{{\rm{B}}}T)}^{3}\) in Eq. (18) is replaced by Δ3/12.
For magnetic field applied in the ab plane, the electric polarization at high temperatures,
is proportional to H6 and oscillates six times as φ varies by 2π, in agreement with Eq. (2) (a6 ∝ T−5). At zero temperature, \({({k}_{{\rm{B}}}T)}^{5}\to {\Delta }^{5}/90\).
The coefficients a4 and a6 in Eqs. (1, 2) can be estimated from the low-field slopes of experimental data shown in Fig. 3. As demonstrated in the insets to Fig. 3, they indeed follow the expected a4 ∝ T−3 and a6 ∝ T−5 behavior.
The ME coupling ∝ Ec, which leads to Eq. (16) for the magnetically induced polarization,
also gives rise to the electrically induced magnetization, \(\delta {\bf{M}}=-\frac{\partial {f}_{{\rm{m}}e}}{\partial {\bf{H}}}\).
Figure 4a shows the magnetization at Ec = 0 (Eq. (13)) plotted vs the angle φ describing the orientation of the magnetic field in the ab plane. In general, M is not parallel to H. In the saturation regime, it depends on the sign of the magnetic field projection on the easy axes of Ho ions, but not on the magnetic field strength. Figure 4b shows the electrically induced magnetization, δM, divided by Ec. M and \({\left(d{\bf{M}}/d{E}_{c}\right)}_{{E}_{c} = 0}\) have opposite symmetries with respect to φ → − φ: Mx is a symmetric function of φ and My, Mz are antisymmetric, whereas for dM/dEc it is the other way around.
a Magnetization in zero electric field (arbitrary units) vs the angle φ describing the orientation of the magnetic field in the ab-plane, \({\bf{H}}={H}_{0}(\cos \varphi ,\sin \varphi ,0)\), for H0 = 4 T and T = 5 K. Red, blue, and green lines show, respectively, the x, y and z components of M. b. Angular dependence of \({\left.(d{\bf{M}}/d{E}_{c})\right|}_{{E}_{c} = 0}\) (arbitrary units) for H0 = 4 T and T = 5 K. Red, blue, and green lines show, respectively, the x, y, and z components of the magnetization derivative.
Interestingly, the inverse ME response is amplified when the magnetic field is normal to the easy axis of one of the Ho-sublattices. At zero temperature and for μ0H ≫ Δ, δM shows sharp peaks at (mi ⋅ H) = 0,
Data availability
The data that support the findings of this study are available from the authors on reasonable request, see author contributions for specific data sets.
Code availability
The code of the model used to produce the fits will be provided by A.A.M. or M.M. upon request.
References
Manipatruni, S., Nikonov, D. E. & Young, I. A. Beyond CMOS computing with spin and polarization. Nat. Phys. 14, 338–343 (2018).
Bibes, M. & Barthélémy, A. Towards a magnetoelectric memory. Nat. Mater. 7, 425–426 (2008).
Kleemann, W. Magnetoelectric spintronics. J. Appl. Phys. 114, 027013 (2013).
Matsukura, F., Tokura, Y. & Ohno, H. Control of magnetism by electric fields. Nat. Nanotechnol. 10, 209–220 (2015).
Cheong, S.-W. & Mostovoy, M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 6, 13–20 (2007).
Spaldin, N. A. & Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212 (2019).
Landau, L. D. & Lifshitz, E. M. Electrodynamics of continuous media. Course of theoretical physics (Butterworth-Heinemann, Oxford, 1999).
Dzyaloshinskii, I. E. On the magneto-electrical effect in antiferromagnets. Sov. Phys. JETP 10, 628–629 (1960).
Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D: Appl. Phys. 38, R123–R152 (2005).
Astrov, D. N. The magnetoelectric effect in antiferromagnetics. Sov. Phys. JETP 11, 708–709 (1960).
Rivera, J.-P. The linear magnetoelectric effect in LiCoPO4 revisited. Ferroelectrics 161, 147–164 (1994).
Spaldin, N. A., Fiebig, M. & Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys.: Condens. Matter 20, 434203 (2008).
Pimenov, A. et al. Possible evidence for electromagnons in multiferroic manganites. Nat. Phys. 2, 97–100 (2006).
Zimmermann, A. S., Meier, D. & Fiebig, M. Ferroic nature of magnetic toroidal order. Nat. Commun. 5, 4796 (2014).
Kocsis, V. et al. Identification of antiferromagnetic domains via the optical magnetoelectric effect. Phys. Rev. Lett. 121, 057601 (2018).
Sannikov, D. G. Phenomenological theory of the magnetoelectric effect in some boracites. J. Exp. Theor. Phys. 84, 293–299 (1997).
Khanh, N. D. et al. Magnetic control of electric polarization in the noncentrosymmetric compound (Cu,Ni)B2O4. Phys. Rev. B 87, 184416 (2013).
Seki, S., Yu, X. Z., Ishiwata, S. & Tokura, Y. Observation of skyrmions in a multiferroic material. Science 336, 198–201 (2012).
Ascher, E. Higher-order magneto-electric effects. Philos. Mag. A 17, 149–157 (1968).
Schmid, H. Magnetoelectric effects in insulating magnetic materials. Proc. SPIE 4097, 12–24 (2000).
Liang, K.-C. et al. Giant magnetoelectric effect in HoAl3(BO3)4. Phys. Rev. B 83, 180417 (2011).
Kaminskii, A. A., Sarkisov, S. E., Mill, B. V. & Khodzhabagyan, G. G. New inorganic material with a high-concentration of Nd3+ ions for obtaining stimulated-emission at the 4F3/2-4I11/2 and 4F3/2-4I13/2 transitions. Inorg. Mater. 18, 1189–1191 (1982).
Kaminskii, A. A., Mill, B. V., Silvestrova, I. M. & Khodzhabagyan, G. G. Nonlinearly-active material (La1−xNdx)3Ga5SiO14. Izv. Acad. Sci. USSR, Phys. Ser. 47, 1903–1909 (1983).
Mill, B. V. & Pisarevsky, Y. V. Langasite-type materials: from discovery to present state. In Proc. 2000 IEEE/EIA International Frequency Control Symposium and Exhibition (Cat. No. 00CH37052), 133–144 (Institute of Electrical and Electronics Engineers, Piscataway, 2000) https://doi.org/10.1109/FREQ.2000.887343.
Andreev, I. A. & Dubovik, M. F. New piezoelectric langasite La3Ga5SiO14-material with zero temperature-coefficient of elastic oscillation particles. JETP Lett. 10, 487–491 (1984).
Fritze, H. & Tuller, H. L. Langasite for high-temperature bulk acoustic wave applications. Appl. Phys. Lett. 78, 976–977 (2001).
Stade, J., Bohaty, L., Hengst, M. & Heimann, R. Electro-optic, piezoelectric and dielectric properties of langasite (La3Ga5SiO14), langanite (La3Ga5.5Nb0.5O14) and langataite (La3Ga5.5Ta0.5O14). Cryst. Res. Technol. 37, 1113–1120 (2002).
Kong, H. et al. Growth, properties and application as an electrooptic q-switch of langasite crystal. J. Cryst. Growth 254, 360–367 (2003).
Marty, K. et al. Magnetic and dielectric properties in the langasite-type compounds: A3BFe3D2O14 (A = Ba, Sr, Ca; B = Ta, Nb, Sb; D = Ge, Si). Phys. Rev. B 81, 054416 (2010).
Loire, M. et al. Parity-broken chiral spin dynamics in Ba3NbFe3Si2O14. Phys. Rev. Lett. 106, 207201 (2011).
Ramakrishnan, M. et al. Field-induced double spin spiral in a frustrated chiral magnet. npj Quantum Mater. 4, 60 (2019).
Maksimov, B. A. et al. Absolute structure of La3Ga5SiO14 langasite crystals. Crystallogr. Rep. 50, 751–758 (2005).
Bordet, P. et al. Magnetic frustration on a Kagomé lattice in R3Ga5SiO14 langasites with R = Nd, Pr. J. Phys.: Condens. Matter 18, 5147–5153 (2006).
Zvezdin, A. K. et al. Magnetoelectric effects in gadolinium iron borate GdFe3(BO3)4. JETP Lett. 81, 272–276 (2005).
Zvezdin, A. K. et al. Magnetoelectric and magnetoelastic interactions in NdFe3(BO3)4 multiferroics. JETP Lett. 83, 509–514 (2006).
Ivanov, V. Y., Kuzmenko, A. M. & Mukhin, A. A. Magnetoelectric effect in ytterbium aluminum borate YbAl3(BO3)4. JETP Lett. 105, 435–441 (2017).
Popov, A. I., Plokhov, D. I. & Zvezdin, A. K. Quantum theory of magnetoelectricity in rare-earth multiferroics: Nd, Sm, and Eu ferroborates. Phys. Rev. B 87, 024413 (2013).
Zvezdin, A. K., Levitin, R. Z., Popov, A. I. & Silantiev, V. I. Field dependence of the magnetostriction constants of rare-earth iron garnets. Sov. Phys. JETP 53, 771–775 (1981).
Babushkin, G. A., Zvezdin, A. K., Levitin, R. Z., Orlov, V. N. & Popov, A. I. Theoretical and experimental investigations of the magnetostriction of paramagnetic rare-earth garnets Tb3Ga5O12 and Dy3Al5O12. Sov. Phys. JETP 85, 1366–1376 (1983).
Vedernikov, N. F., Zvezdin, A. K., Levitin, R. Z. & Popov, A. I. Magnetic linear birefringence of rare-earth garnets. Sov. Phys. JETP 66, 1233–1242 (1987).
Vedernikov, N. F., Zvezdin, A. K., Levitin, R. Z. & Popov, A. I. Magnetostriction of paramagnetic rare-earth garnets. Sov. Phys. JETP 67, 1719–1726 (1988).
Khanh, N. D., Abe, N., Kimura, S., Tokunaga, Y. & Arima, T. Manipulation of electric polarization with rotating magnetic field in a honeycomb antiferromagnet Co4Nb2O9. Phys. Rev. B 96, 094434 (2017).
Konstantinova, A. F., Golovina, T. G. & Dudka, A. P. Anisotropy of optical activity in langasite family crystals. Crystallogr. Rep. 63, 200–206 (2018).
Acknowledgements
We thank Peter Kregsamer and Christina Streli for help in determining the actual Ho-content in our samples. This work was supported by the Russian Science Foundation (16-12-10531) and by the Austrian Science Funds (W 1243, I 2816-N27, P 27098-N27).
Author information
Authors and Affiliations
Contributions
A.P., A.A.M., and M.M. supervised the project; Th.K. and A.S. designed the experiment; B.V.M. grew the samples; L.W., L.B., A.P., E.C., D.S., and V.Y.I. characterized the samples using various techniques; L.W., V.Y.I., and A.M.K. conducted the experiments and analyzed the data under the supervision of A.P. and A.A.M.; N.V.K., A.K.Z., A.I.P., A.A.M., and M.M. developed the theory. A.P., L.W., A.A.M., and M.M. contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weymann, L., Bergen, L., Kain, T. et al. Unusual magnetoelectric effect in paramagnetic rare-earth langasite. npj Quantum Mater. 5, 61 (2020). https://doi.org/10.1038/s41535-020-00263-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00263-9
This article is cited by
-
Confirming the trilinear form of the optical magnetoelectric effect in the polar honeycomb antiferromagnet Co2Mo3O8
npj Quantum Materials (2022)