Introduction

Topological materials have ushered in a new era in condensed matter research since the discovery of the quantum Hall effect. Over the years, a few material systems have been reported as topological insulators such as Bi1−xSbx1 and Bi2Se32, topological semimetals such as Cd3As23,4,5, Na3Bi6,7, YbMnBi28, BaMnSb29, and topological superconductors such as CuxBi2Se3, Sn1−xInTe, and others10,11,12. In an ordinary semimetal, there is a small overlap between the valence and conduction bands. However, in a topological Dirac semimetal (TDSM), the inverted bands contact only at discrete Dirac points in momentum space with linear energy dispersions. The behavior of these fermions is governed by the relativistic Dirac equation13,14. In a TDSM, spin–orbit coupling (SOC) does not open up a gap, and the Dirac points are protected by the time-reversal and inversion symmetries3,15. If symmetries are broken, these materials can be driven into various other topological phases. For instance, the breaking of either the time-reversal or inversion symmetry can drive a TDSM to a Weyl semimetal3. Moreover, topological materials can also exhibit superconductivity which is an extremely attractive feature for quantum technological applications12.

One key indication of the possible topological phases in a material is the inversion of energy bands at high-symmetry points in the Brillouin zone16. These features can be investigated through band structure calculations, which have been quite successful in predicting topological phases in a number of material systems17,18,19,20,21. Recently, Nie et al.22 have investigated the topological phases in a chain-compound TaSe3 through first-principles calculations. The Z2 invariants (ν0;ν1ν2ν3) were obtained for this material, which can be used to distinguish if the system is ordinary or topologically non-trivial. Here, ν0 is called the strong topological index, and a value of ν0 = 1 indicates a “strong” topological insulator (STI) phase with an odd number of Dirac cones on the surface, which are robust against weak time-reversal invariant perturbations. A “weak” topological insulator phase is identified when ν0 = 0, and one of the indices ν1, ν2, or ν3, known as the weak topological indices, is nonzero16. The calculations for TaSe3 revealed the Z2 invariants (ν0;ν1ν2ν3) to be (1;100)22, indicating a strong three-dimensional TI with guaranteed Dirac states on the surfaces. Furthermore, band calculations indicate that there is a band inversion even without spin–orbit coupling (SOC) in TaSe322.

While there have been investigations on various physical properties23,24,25,26,27,28,29, the topological properties of TaSe3 have remained experimentally unexplored, except for a recent preprint30. This is in part due to the multiple bands with two identical electron bands related to band inversion, and one hole band involving no band inversion. In order to distinguish them, information from individual bands has to be separated. In this article, we report the experimental investigation of the Fermi surface topology of TaSe3 single crystals. Shubnikov-de Haas (SdH) oscillations of both the longitudinal and Hall conductivities are clearly observed. Fast Fourier transformation (FFT) analysis of the SdH oscillations indicates two frequencies, Fα ≈ 97 T and Fβ ≈ 186 T. By constructing the Landau level fan diagram for each oscillation, we obtain the Berry phase \({\it{\Phi }}_{\mathrm{B}}^\upalpha\) ≈ 1.1π and \({\it{\Phi }}_{\mathrm{B}}^\upbeta\) ≈ 0(3D) − 0.16π(2D). This indicates that the α band is topologically non-trivial, while the β band is trivial. In addition, we observe extremely large magnetoresistance (XMR) in this material which reaches about 7 × 103% for H = 14 T at T = 1.9 K, and follows the Kohler’s scaling law. The quadratic nature of the MR with respect to magnetic field points towards a high degree of electron–hole compensation, supported by our Hall effect data.

Results and discussion

Crystal structure and magnetotransport

Figure 1a shows the X-ray diffraction (XRD) pattern for a single crystal of TaSe3 at room temperature. The XRD peaks are consistent with a monoclinic structure with the space group P21/m. Due to its malleable nature, the single crystal was not perfectly flat on the sample platform, producing a weak \(40\bar 5\) peak at 2θ ≈ 50°, unexpected from the \(10\bar 1\) plane (Fig. 1a). For further confirmation, we performed single crystal XRD measurements at room temperature, which also revealed the same monoclinic structure. The lattice parameters, a = 9.834(2) Å, b = 3.496(1) Å, c = 10.421(3) Å, and β = 106.237(6)° were obtained through a Rietveld refinement of the single crystal XRD data. The crystal structure of TaSe3 consists of infinite, trigonal prismatic chains along the crystallographic b-axis, as shown in the left side of Fig. 1b. A single linear chain is formed by stacking prismatic cages along the b-axis. At the center of each cage there is a Ta atom, coordinated with six Se atoms at the corners. However, the neighboring chains are inequivalent, which are named as type-I and type-II chains (Fig. 1b). The shorter distance between the Se atoms in type-I chains enables the formation of strong covalent p–p bonding between the two Se atoms, whereas this bond is broken in the type-II chains due to the longer distance. According to band structure calculations, these Se atoms in the type-II chains form bonds with the Ta atoms from the neighboring chains, which is primarily responsible for the band inversion in this material22.

Fig. 1: Crystal structure, magnetization, and electrical resistivity of TaSe3.
figure 1

a XRD pattern of a TaSe3 single crystal. Inset: Picture of a TaSe3 single crystal. b Crystal structure of TaSe3. The larger blue and smaller red spheres represent Ta and Se atoms, respectively. c Temperature dependence of the magnetic susceptibility [χ(T)] at H = 1 kOe. Inset: Magnetic field dependence of the magnetization [M(H)] at T = 1.85 K. d ρb vs. temperature (T). Solid red curve indicates the fitting of the data to the Bloch–Grüneisen formula. Inset: ρb(T) for T < 60 K. The green solid line represents a fit to the formula ρb(T) = ρ0 + CTm (see text).

Full size image

Figure 1c shows the temperature dependence of the magnetic susceptibility [χ(T)] measured at H = 1 kOe, which is negative over the entire temperature range. This indicates a diamagnetic behavior in TaSe3, which is also supported by the negative and linear magnetic field dependence of the magnetization [M(H)], measured at T = 1.85 K as shown in the inset of Fig. 1c. Since the negative χ is not suppressed up to 7 T, the diamagnetism is not related to superconductivity but to the core electron contribution of TaSe3.

Figure 1d shows the temperature dependence of the b-axis resistivity (ρb) of TaSe3 at zero magnetic field in the temperature range of 1.9–305 K. The resistivity shows metallic behavior, which decreases with decreasing temperature from ρb (300 K) = 1910 µΩ cm to ρb ((1.9 K) = 14 µΩ cm. This corresponds to a residual resistivity ratio [RRR = ρ (300 K)/ρ (1.9 K)] of 136. The RRR of this sample is similar to or exceeds the previously reported values for this material23,24,25,26,27,28,29, indicating the high quality of our single crystals. In the temperature range of T = 60–300 K, the ρ(T) data follow the Bloch–Grüneisen (BG) law

$$\rho \left( T \right) = \rho _0 + A\left( {\frac{T}{{\theta _{\mathrm{D}}}}} \right)^k\mathop {\int}\nolimits_0^{\theta _{\mathrm{D}}/T} {\frac{{x^k{\mathrm d}x}}{{(e^x - 1)(1 - e^{ - x})}}}.$$
(1)

Here, ρ0, A, and θD are the residual resistivity, electron–phonon interaction constant, and Debye temperature, respectively. The red solid line in Fig. 1d represents the fitting of the data with Eq. (1). The fitting yields A = 8.23 ± 0.03 mΩ cm, θD = 310 ± 2 K, and the exponent k = 4.6. The value of k is close to 5 expected for simple metals with dominant electron–phonon scattering. On the other hand, ρb(T) at low temperatures (T < 60 K) follows a power law behavior given by ρb(T) = ρ0 + CTm, as shown in the inset of Fig. 1d. The residual resistivity ρ0 = 14.5 ± 0.5 µΩ cm and the exponent m = 2.5 ± 0.02 were obtained from the fit. While there is electron–phonon scattering, it had been argued that in quasi 1D materials, the electron–electron Umklapp scattering can become the dominant scattering mechanism at low temperatures, when the energy (kBT) is smaller than the inter-chain interaction energy31,32. In this scenario, the exponent m takes a value between 2 and 331,32. Similar behavior was previously reported in TaSe331. Thus, we consider that the electron–electron Umklapp scattering plays the dominant role in scattering at low temperatures in TaSe3.

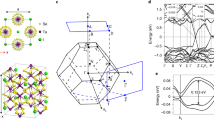
According to Fig. 1a, the flat surface of the as-grown TaSe3 single crystals is normal to the [\(10\bar 1\)] direction. For probing the magnetic field (H) effect, we apply H normal to the flat surface, i.e., H ⊥ [\(10\bar 1\)]. For easy discussion, the applied field direction is indicated with respect to the Brillouin zone (BZ) and Fermi surface pockets, as shown in Fig. 2a, b (adapted from ref. 22), respectively. Figure 2c shows the temperature dependence of ρb at various magnetic fields up to 14 T. This and the rest of the measurements were conducted using a sample with RRR = 107. In the presence of an applied magnetic field normal to the current (H ⊥ I), the ρb(T) curves maintain metallic behavior at high temperatures, where the resistivity decreases with decreasing temperature until reaching a minimum at Tm. Below this temperature, the resistivity keeps increasing until a plateau-like region is reached at Ti. The onset temperature Tm is identified as the point where ∂ρb(T, H)/∂T = 0, whereas Ti is the point where ∂ρb(T, H)/∂T is minimum. The inset of Fig. 2c shows the magnetic field dependence of these two characteristic temperatures, both increasing with increasing magnetic field. However, the increase in the onset temperature Tm is more drastic than that of Ti.

Fig. 2: Brillouin zone, Fermi surface, and magnetotransport measurements.
figure 2

a Bulk Brillouin zone (BZ) of TaSe3 with the high-symmetry points and the projected surface BZ, highlighted in green22. b Fermi surface with the hole (purple) and electron (yellow–green) pockets22. The closed electron pockets near the B point and the hole pocket [~k1 into the page] are enlarged for clarity. The red arrow indicates the applied field direction. The red lines indicate cyclotron orbits for which SdH oscillations were observed. c ρb vs. T measured at various magnetic fields with H ⊥ I. Inset: H dependence of the two characteristic temperatures: Tm (black squares) is defined as the point where ∂ρb(T, H)/∂T = 0 and Ti (blue circles) is where ∂ρb(T, H)/∂T is minimum. d Determination of the resistivity change between 0 and 7 T, described by Eq. (3). The black, blue, and purple symbols represent ρb(0 T), ρb(7 T), and ρb(7 T) − ρb(0 T), respectively. The solid green and magenta lines represent fits to Eq. (3) and Δρ = αHn/ρ(T, 0)n−1, respectively. e MR vs. H at various temperatures. f Kohler’s plot of the MR data (MR vs. H/ρ0) in the temperature range of T = 1.9–12 K. Inset: MR vs. H/ρ0 at T = 4 K. The solid blue line represents a fit to Eq. (2). (a, b are adapted with permission from ref. 22, copyright (2018) by The American Physical Society).

Full size image

Kohler’s scaling law

The magnetic field-induced resistivity upturn and XMR have been frequently observed in topological materials33,34,35,36,37. Several mechanisms are proposed to explain these features, such as field-induced metal-to-insulator transition, electron–hole compensation, topological protection, and so on36,38,39. Recently, it was demonstrated that this type of field-induced resistivity upturn could be explained within the framework of the Kohler’s scaling law without invoking any topological considerations35,40. The Kohler’s scaling law is given by41,42

$${\mathrm{MR}} = \alpha \left( {H{\mathrm{/}}\rho _0} \right)^n$$
(2)

with α and n being constants. Since MR is given by \(\frac{{\rho \left( {T,H} \right)\, - \,\rho (T,0)}}{{\rho (T,0)}}\), Eq. (2) can be rearranged and written as

$$\rho \left( {T,H} \right) = \rho \left( {T,0} \right) + \alpha \frac{{H^n}}{{\rho \left( {T,0} \right)^{n - 1}}}.$$
(3)

In light of Eq. (3), ρ(T, H) consists of two terms: temperature dependence of the resistivity at zero field [ρ(T, 0)] and the magnetic-field-induced resistivity [Δρ = αHn/ρ(T, 0)n−1]. Since these two terms have opposite temperature dependence, the minimum in the ρ(T, H) curve arises due to a competition between the two terms35,40,43. For demonstration, we choose ρb(T) at H = 7 T, as shown by the blue symbols in Fig. 2d. The solid green line in the figure represents a fit of the data to Eq. (3) with α = 1.3 × 10−10 (Ω cm)n T−n and n = 1.95. The purple symbols in Fig. 2d represent the difference in the temperature dependence of the resistivity measured at H = 0 and 7 T [Δρ = ρb(7T) − ρb(0T)]. The data was fitted with the second term in Eq. (3), as represented by the solid (magenta) line. We note that Eq. (3) can describe the field-induced resistivity fairly well. Furthermore, the plateau in the ρb(T, H) curves (Fig. 2c) at low temperatures can also be explained through Eq. (3). At low temperatures, ρb(T, 0) = ρ0 becomes very low and practically temperature independent. Therefore, ρ(T, H) ~ αHn/\(\rho _0^{n - 1}\) is constant at low temperatures, giving rise to a plateau.

To confirm the Kohler’s scaling law, we have measured the magnetic field dependence of ρb(T, H) at fixed temperatures with H ⊥ I. Since the measured ρb(T, H) can contain both the longitudinal (ρyy) and Hall (ρxy) contributions, the longitudinal component was isolated from the Hall component by using the relation, ρyy = [ρb(T, +H) + ρb(T, −H)]/2. The MR was then calculated using the standard relation, MR = [ρyy(H) − ρyy(0)]/ρyy(0). Figure 2e shows the MR at indicated temperatures for up to 14 T. We observe the XMR in this material which reaches about 7 × 103% at T = 1.9 K and H = 14 T without showing any sign of saturation. This is comparable to other XMR materials, such as Cd3As244, Na3Bi45, NbP46, TaAs47, WTe233,38, and PtBi2−x37.

The Kohler’s scaling law (Eq. (2)) can describe the motion of electrons in magnetic field for a single band or multiple bands with electron–hole compensation35,41,42. For n = 2, the Kohler’s law [MR = α(H/ρ0)2] can be derived from the two-band model of the electrical resistivity for non-magnetic materials, when the electron and hole carrier concentration is perfectly compensated35. However, Wang et al.35 also argued that MR for an imperfectly compensated system can still obey the Kohler’s law if either or both the mobilities are small. Nevertheless, this law would be violated if α is temperature dependent35. Figure 2f shows the MR at various temperatures plotted against the rescaled magnetic field H/ρ0. Consequently, all the MR curves from T = 1.9–12 K collapse on to a single curve, indicating that the scattering mechanism is the same throughout the relevant temperature and field ranges. This rules out the possibility of a metal-to-insulator transition35,36,48. In addition, the collapse of the MR curves, according to the Kohler’s rule, indicates that the carrier concentration and the mobility ratio of hole-to-electron do not change significantly with temperature49,50. The inset of Fig. 2f shows a fitting of the MR curve at T = 4 K using Eq. (2), yielding α = (1.30 ± 0.01) × 10−10 (Ω cm)n T−n and n = 1.950 ± 0.001. These values are used to fit the ρb(T) data, as shown in Fig. 2d. The value of n depends on the level of carrier compensation. For a system with perfect electron–hole compensation, n should be 235,43. Thus, the value of n = 1.95 for TaSe3 points towards a high degree of electron–hole compensation.

SdH oscillations

As can be seen in Fig. 2e, ρb exhibits SdH oscillations. The SdH oscillations occur in crystalline solids when the density of states is periodically modulated as a function of magnetic field due to the Landau quantization of the energy states in magnetic field51. One of the most useful aspects of SdH oscillations is that it contains information on band topology reflected in the Berry phase. A widely used method to extract the Berry phase is to construct the Landau level fan diagram, where the minima in the SdH oscillations of the conductivity are assigned to an integer Landau level index51. We calculated the longitudinal (σyy) and Hall conductivities (σxy) using the following relations:

$$\begin{array}{l}\sigma _{yy} = \frac{{\rho _{yy}}}{{\rho _{yy}^2 \,+\, \rho _{xy}^2}},\\ \sigma _{xy} = - \frac{{\rho _{xy}}}{{\rho _{yy}^2 \,+\, \rho _{xy}^2}}.\end{array}$$
(4)

Figure 3a shows the longitudinal and Hall conductivities measured at various temperatures for H = 0–14 T. The smooth background of the σyy(H) data was deduced through polynomial fitting, which was then subtracted from the data to obtain the oscillatory component of the conductivity Δσyy. Figure 3b shows σyy(H) vs. H−1 at indicated temperatures. FFT analysis reveals two frequencies with Fα ≈ 97 T and Fβ ≈ 186 T, as shown in Fig. 3c. The FFT frequency (F) and the Fermi surface cross-section (AF) are related by the Onsager relation F = (ħ/2πe)AF. Therefore, Fα and Fβ correspond to Aα = 0.009 Å−2 and Aβ = 0.018 Å−2, respectively. In Fig. 2b, the cyclotron orbits perpendicular to the H direction are depicted by red lines for both electron (yellow–green) and hole (purple) pockets. Note that the two electron pockets are identical22, thus having the same frequency, i.e., Fα. Since the cross-sections are not perfectly circular, it is difficult to accurately estimate the corresponding Fermi wave vectors from the measured cross-section areas.

Fig. 3: Conductivity and SdH oscillations.
figure 3

a Longitudinal conductivity (σyy) (upper panel) and Hall conductivity (σxy) (bottom panel) of TaSe3 for a field range of H = 0–14 T at various temperatures. b Oscillatory conductivity (Δσyy) vs. inverse magnetic field (H−1) at indicated temperatures. c FFT spectrum of the oscillations at various temperatures. d The temperature dependence of the FFT amplitudes of the two principal frequencies (Fα and Fβ) in the FFT spectra. Solid lines represent fits to Eq. (5).

Full size image

Figure 3d shows the temperature dependence of the normalized FFT amplitudes for the α and β bands. The gradual damping of the oscillation amplitudes with increasing temperature can be described by the Lifshitz–Kosevich (LK) equation51,52,53

$$R_T = \frac{{A^\prime (m^\ast{\mathrm{/}}m_0)T}}{{\sinh [A^\prime\left( {m^\ast {\mathrm{/}}m_0} \right)T]}}.$$
(5)

Here, RT, m0, and m* are the FFT amplitude, free electron mass, and effective mass, respectively. The parameter A′ is given by \(A^\prime = \frac{{2{\uppi}^2k_{\mathrm{B}}m_0}}{{{\mathrm{e}}\hbar H_{{\mathrm{eff}}}}}\), where Heff = 2/(1/H1 + 1/H2), with H1 = 5 T and H2 = 14 T being the lower and upper limits of the magnetic field range in which the FFT analysis was conducted. kB and ħ are the Boltzman and Planck constants, respectively. We obtain the effective masses of \(m_\upalpha ^ \ast\) = 0.49m0 and \(m_\upbeta ^ \ast\) = 0.48m0 corresponding to the α and β bands though fitting the FFT amplitude vs. temperature data with Eq. (5), as shown in Fig. 3d.

Berry phase

We have isolated the oscillations corresponding to each frequency (Fα and Fβ) through filtering, and the isolated single frequency oscillations were used to construct the Landau level fan diagram as shown in Fig. 4a, b. The minima in Δσyy(H−1) positions are assigned integer Landau level indices (N), whereas the maxima positions are assigned N + 1/2. According to the Lifshitz–Onsager relationship, N = F/H + ΦB/2π + δ51,52. Here, ΦB is the Berry phase, and δ depends on the dimensionality of the Fermi surface and carrier type. For a two-dimensional (2D) Fermi surface δ = 0, whereas δ = +1/8(−1/8) for the minima (maxima) of a three-dimensional (3D) electron band. On the other hand, δ = −1/8(+1/8) for the minima (maxima) of a 3D hole band. It implies from the Onsager relationship that the slope of N(H−1) plot should correspond to the oscillation frequency, while the intercept can be used to calculate ΦB. The slopes of the straight lines were found to be 97.25 ± 0.03 and 186.2 ± 0.01 T for the α and β bands, respectively. These values are in excellent agreement with the oscillation frequencies identified through FFT analysis. The intercepts were found to 0.56 ± 0.004 and 0.08 ± 0.002 for the α and β bands, respectively. According to band structure calculations22, the α band is 2D (see Fig. 2b). Thus, the corresponding Berry phase is \({\it{\Phi }}_{\mathrm{B}}^\alpha\) = [0.56 ± 0.004] × 2π ≈ [1.120 ± 0.008]π. This indicates a non-trivial topology for the α band. On the other hand, the β band is predicted to be hole-like with the 3D characteristic (see Fig. 2b). With H ⊥ [\(10\bar 1\)], Fβ corresponds to the maxima of the β Fermi pocket, with δ = +1/8. Thus, we obtain \({\it{\Phi }}_{\mathrm{B}}^\upbeta\)(3D) = [(0.08 ± 0.002) − 1/8] × 2π = [−0.09 ± 0.003]π ≈ 0. Since it is disc shaped (Fig. 2b), \({\it{\Phi }}_{\mathrm{B}}^\upbeta\)(2D) = [0.08 ± 0.002] × 2π ≈ [0.160 ± 0.004]π using δ = 0. The non-trivial Berry phase for the α band and a trivial one for the β band are consistent with first-principles calculations22. Interestingly, an oscillation frequency of 175 T was identified to correspond to a non-trivial band in ref. 30. At present, it is unclear whether the slight frequency difference can make such a dramatic change in the topology of the β band.

Fig. 4: Landau level fan diagrams.
figure 4

a Landau level fan diagram for the α band at T = 1.9 K, where N is obtained from Δσyy and plotted as a function of H−1. Solid line represents a linear fit to the data. b The Landau level fan diagram for the β band at T = 1.9 K.

Full size image

Hall effect and two-band fitting

To further understand the electronic structure of TaSe3, we have investigated the Hall effect at low temperatures. Figure 5a shows the results of Hall resistivity (ρxy) measurements up to H = 14 T between temperatures T = 1.9–8 K. The field dependence of the Hall resistivity [ρxy(H)] shows a non-linear behavior, which changes from positive at lower fields to negative at high fields (H > 7.5 T). This behavior suggests that both types of charge carriers are responsible for the Hall effect. The ρxy(H) curves are almost identical in the temperature range of T = 1.9–8 K, indicating that the carrier concentrations and mobilities do not significantly change in this temperature range50. Clear SdH oscillations can be seen for H > 9 T, especially at low temperatures. Since ρxy ≪ ρyy, multiple band analysis of the Hall data should be conducted through the Hall conductivity σxy50,51, which was calculated through Eq. (4). For a system with multi-band transport, σxy can be expressed as

$$\sigma _{xy} = {\mathrm{e}}H\left[ {\frac{{n_{\mathrm{h}}\mu _{\mathrm{h}}^2}}{{1 + \left( {\mu _{\mathrm{h}}H} \right)^2}} - \frac{{n_{\mathrm{e}}\mu _{\mathrm{e}}^2}}{{1 + \left( {\mu _{\mathrm{e}}H} \right)^2}}} \right].$$
(6)

Here, nh(ne), μh(μe) are the concentration of holes (electrons) and mobilities of holes (electrons), respectively. Figure 5b shows the magnetic field dependence of the Hall conductivity at T = 2 K, and the corresponding fitting using Eq. (6). We can see that the two-band model fits the σxy(H) data at T = 2 K quite well. Similarly, Eq. (6) generated good fits for the σxy(H) data in the temperature range of T = 2–8 K. The carrier concentrations and mobilities were obtained from fitting, and their temperature dependence in the range of T = 2–8 K is shown in Fig. 5c, d. The hole concentration remains slightly higher than the electron concentration throughout the temperature range, whereas the mobility of the electrons remains higher than that of holes. From the semiclassical two-band model, the MR of non-magnetic materials with perfectly compensated electron and hole-type carriers (nh = ne) can be described by MR ≈ μeμhH2 35,54,55. We have used the carrier mobilities obtained from the Hall conductivity data to estimate the MR at various temperatures through this relation. The MR curves estimated from the mobilities are remarkably similar to that obtained from experiment, as demonstrated in the inset Fig. 5d for T = 2 K. The slight difference between them could be due to the imperfect carrier compensation in TaSe3.

Fig. 5: Hall effect and two-band fitting.
figure 5

a Hall resistivity (ρxy) vs. H at various temperatures. b Hall conductivity (σxy) vs. H at T = 2 K. Solid red line represents a fit to the two-band model (Eq. (6)). c Temperature dependence of hole and electron concentrations (left vertical axis) and nh/ne (right vertical axis). d Temperature dependence of the mobilities of the holes and electrons. Inset: MR vs. H at T = 2 K from experiment \(\left[ {{\mathrm{MR}} = \frac{{\rho \left( H \right) \,-\, \rho (0)}}{{\rho (0)}}} \right]\) and mobilities [MR = μhμeH2], represented by the brown and green lines, respectively. The error bars in c, d represent standard errors obtained through fitting the experimental data to Eq. (6).

Full size image

At T = 2 K, the fitting yielded the hole and electron concentrations: nh = 1.25 × 1019 cm−3, ne = 1.12 × 1019 cm−3, and mobilities μh = 3.6 × 103 cm2 V−1 s−1, μe = 7.8 × 103 cm2 V−1 s−1. The relatively low carrier concentrations are consistent with the semimetallic nature of TaSe3. For TaSe3, the relatively lower mobility (≈103 cm2 V−1 s−1) is due to its relatively “heavier” effective mass (m* ≈ 0.49m0) compared to other semimetals4,34,36,50,56,57. In the temperature range of T = 2–8 K, the ratio nh/ne ≈ 1.1, as shown in Fig. 5c. This feature points towards a high degree of carrier compensation, making the Kohler’s scaling law well justified (Fig. 2f).

To summarize, we have grown single crystals of a chain-compound TaSe3 through the chemical vapor transport method. We observed the XMR effect in this material which reaches up to 7 × 103% at T = 1.9 K for H = 14 T applied normal to the b-axis. The XMR obeys the Kohler’s scaling law as evident from the collapse of the MR curves measured at different temperatures on to a single curve when plotted as MR = α(H/ρ0)n. Furthermore, both the longitudinal and Hall conductivities exhibit SdH oscillations at low temperatures. A FFT analysis of the SdH oscillations of the electrical conductivity revealed two fundamental frequencies, Fα ≈ 97 T and Fβ ≈ 186 T. The Berry phases \({\it{\Phi }}_{\mathrm{B}}^\alpha\) ≈ 1.1π and \({\it{\Phi }}_{\mathrm{B}}^\beta\) ≈ 0(3D) − 0.16π(2D) for the corresponding α and β bands were extracted through the construction of Landau level fan diagrams. This indicates the non-trivial Berry phase for the α band and the trivial one for the β band. Comparing with band structure calculations22, we found that the non-trivial α band is the 2D electron pocket, whereas the trivial β band represents the hole pocket. An analysis of the Hall conductivity revealed two types of carriers, whose concentrations and mobilities were calculated. The obtained electron and hole concentrations are very close, pointing towards a nearly perfect electron–hole compensation in this material. The XMR is likely to have originated from this nearly perfect carrier compensation.

Compared to other TDSMs, a distinguishing feature of TaSe3 is its quasi 1D crystal structure. As predicted in ref. 22, this unique structure can host various topological phases, such as 3D STI, 3D WTI, and Dirac semimetal phases under different strains. It is thus an ideal material system for studying the structure–topological property relationship. Future investigations into the strain or pressure effects on TaSe3 could offer valuable new insights.

Methods

Sample synthesis

Single crystals of TaSe3 were grown through the chemical vapor transport method. High purity (better than 99.9%) powder of Ta and Se with a molar ratio of 1:3.3 were mixed together and pressed into a pellet. The excess Se acts as the transport agent. The pellet was sealed in an evacuated quartz tube, and placed into a horizontal tube furnace. The end of the quartz tube with the pellet (starting material) was placed in the middle of the tube furnace and heated to 700 °C. The other end of the tube furnace was kept open to the atmosphere, which acted as the cold end, and thus creating a temperature gradient necessary for vapor transport. The furnace was maintained at 700 °C for 14 days, followed by a slow cooling to room temperature. Finally, thin 1D-like single crystals with shiny surfaces were obtained.

Measurements

Single crystal XRD measurements were carried out at room temperature using a Bruker Kappa Apex-II and a PANalytical Empyrean X-ray diffractometer. Electrical resistivity and Hall effect measurements were carried out using the standard four-probe technique in a physical property measurement system (PPMS, Quantum Design) for up to 14 T, and in a temperature range of T = 1.9–305 K. The electrical contacts were made using gold wires attached to the sample through epoxy. Hall effect data were measured in both positive and negative field and then subtracted to eliminate the lead-offset voltage.