Introduction

First-principle calculation within the framework of density function theory (DFT) has played an important role in understanding the iron-based superconductors. For the high-temperature paramagnetic (PM) phase, the standard local density approximation (LDA) or its generalized gradient approximation (GGA) extension can already qualitatively describe the Fermi surface topology and its orbital components1,2,3. For the low-temperature magnetic phase, the local spin density approximation (LSDA) or spin-polarized GGA (sGGA) can obtain the correct ground-state spin order in most cases1,2,4. Additional corrections to the electronic correlation effects, e.g., the dynamical mean-field theory (DMFT), further reduce the quantitative discrepancies, such as the overestimation of the band width and the magnetic moment5,6.

However, a first-principle description of the nematic order remains elusive. Dictated by a fourfold rotational (C4) symmetry breaking, the nematic phase remains as a PM metal7. The attempt to explicitly break the C4 symmetry by straining the lattice in the DFT simulation results in only negligible changes on the electronic structure8, which is not surprising, since there is strong experimental evidence suggesting that the nematic order is of an electronic origin9.

Useful insights can be gained from different perspectives7. One scenario that finds a wide range of applications in iron pnictides is to view it as a precursor of the stripe antiferromagnetic phase, in which the spin quadrupolar fluctuation first diverges before the ordering of the spins10,11,12. The other is to invoke a spontaneous orbital ordering13,14,15. For a highly correlated material, the “truth” probably lies between. Despite very different microscopic origins, by symmetry, the formulated order parameters (OPs) all belong to the one-dimensional B1g irreducible representation (irrep) of the D4h point group, i.e, Ising nematicity. Therefore, these OPs are intertwined16, and in reality electronic nematicity manifests in both the spin and the orbital degrees of freedom concurrently. There is no sharp criterion for distinguishing them.

From the DFT perspective, it is difficult to take a composite spin order into account. Nevertheless, mature orbital-resolved approaches, e.g., DFT+U17 and hybrid functional18, allow probing potential instabilities in the orbital channel. FeSe represents an ideal platform to perform this numerical experiment, because no magnetic order has thus far been observed in bulk FeSe, unless high pressure is applied19,20. This provides a chance to study nematicity disentangled from spin ordering, and it is reasonable to speculate that in this case the orbital instability, if exists, can be detected by DFT+U and hybrid functional calculations. In addition, inspired by the high superconducting transition temperature of monolayer FeSe on SrTiO3 substrate21,22, extensive experimental data have been collected and crosschecked, in particular high-resolution angle-resolved photoemission spectroscopy (ARPES) data8,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38, and thus systematic evaluation of the calculation results is possible.

In previous theories, orbital splitting with opposite signs around Γ and M points is the dominant order parameter reproducing the ARPES observations39,40,41, but this OP cannot arise from mean-field treatment of local correlations on single Fe atoms, and sophisticated many-body theory has to be employed40,41.

Here, we show that the important features of the nematic phase can actually be captured by careful treatment of local correlations within the state-of-the-art first-principle framework. The results suggest a predominant nematic OP belonging to the two-dimensional Eu irreducible representations of the D4h point group. The coexistence of C4 rotational and inversion symmetry breaking associated with the Eu OP is found as the key to reproduce the experimental energy bands and Fermi surface.

Results and discussion

Nematic solutions

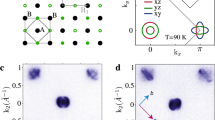
Figure 1(a) schematically summarizes three self-consistent solutions emerged in our DFT+U calculation: α-solution is the symmetric one commonly obtained in previous study; β and γ are the two symmetry-breaking solutions not known before. Within our calculation framework, the γ-solution presents as the lowest-energy state. Figure 1(b) shows the electron-density contour of the α solution [ρα(r)]. Figure 1(c, d) shows the differences between the electron-density contour of the β and γ solutions [ρβ/γ(r)] and ρα(r).

Fig. 1: Self-consistent symmetric and symmetry-breaking solutions.
figure 1

a A schematic illustration of multiple self-consistent solutions in the energy landscape. b Charge density contour of the symmetric solution (ρα) with a1,2 as the two lattice vectors of the 2-Fe unit cell; c, d Charge density change of the two symmetry-breaking solutions (δρβ and δργ). The blue (yellow) color of the isovalue contour stands for the positive (negative) sign of δρ. The zoomed-in distribution of δρ in three dimensions around a single Fe, i.e., the orbital-order parameters \({\Delta }_{{{B}}_{1{\rm{g}}}}\) and \({\Delta }_{{{E}}_{{\rm{u}}}}\) are displayed below. The inset shows the three generators of the P4/nmm/\({\mathcal{T}}\cong {{D}}_{4\rm{h}}\) point group. The dashed gray lines are the normals of the reflection mirrors, which pass an Fe atom.

Full size image

In Fig. 2, we reproduce the band strucuture and Fermi surface of the symmetric phase, which has been well established in the literature1,2,3. An impressive achievement of DFT is the capability of capturing the band connections, orbital components, and Fermi surface topology qualitatively, despite the significantly overestimated band width42. Overall, the DFT+U results of the symmetric α solution shown in Fig. 2(c, d) are not much different from the plain DFT ones [See, for example, Chpt. 8 in ref. 1]. Turning to the nematic phase Fig. 3(a, b), a series of band reconstructions are clearly resolved in recent ARPES data25,27,28,29,30,31,32,37,38,43,44. It is striking that the lowest-energy γ solution captures nearly all the qualitative features. Specifically, around Γ, the dxz and dyz bands are clearly split, and the hole Fermi surface becomes anisotropic. Around M, the bands remain largely unchanged on the Σx side, whereas on the Σy side, the crossing between the dxz and dyz bands is gapped out, regrouping the bands into a hybridized upper branch and a lower branch. One remarkable consequence is that the electron Fermi surface loses the lobes along the gapped direction, which is termed as the “missing electron pocket”37, as also observed in refs 25,27,28,29,30,31,32,38,43,44.

Fig. 2: Band structure and Fermi surface of the symmetric phase.
figure 2

The schematics of experimental results (a) and (b) are replotted based on the ARPES data in ref. 37; c, d are the calculated bands and kz = 0 Fermi surface slices of the symmetric α solution. The color of the bands and Fermi surfaces denotes the orbital components [inset of a], following the convention of ref. 37. b1 and b2 are the two reciprocal vectors of the 2-Fe Brillouin zone. The dashed square shows the 1-Fe Brillouin zone, in which Γ − Σx (Σy − Γ) corresponds to the x(y) direction.

Full size image
Fig. 3: Band structure and Fermi surface of the nematic phase.
figure 3

The schematics of experimental results (a) and (b) are replotted based on the ARPES data in ref. 37; c, d and e, f are the numerical results of the γ and β solutions.

Full size image

The β solution captures the hole band splitting, but it fails to reproduce the characteristic “one-sided” gapping. The β bands can be largely viewed as a momentum-independent upward shift of the dxz bands. In contrast, the γ bands have a more complicated structure.

We note that Fig. 3(c, d) are not fine-tuned results. In Fig. 4, we switch to a different version of the +U correction, and benchmark the DFT+U bands to the hybrid functional results. The latter contains no material-specific parameters, and the lattice constants and atomic positions are fully relaxed. All these methods consistently reproduce the γ solution as the ground state and nicely reproduce the experimental nematic band structures.

Fig. 4: The ground-state (γ solution) band structure calculated by two other methods.
figure 4

a The full orbital-dependent +U correction67; and b HSE0661,62 hybrid functional.

Full size image

Figure 5 shows how the DFT+U total energy of the three solutions change when we manually change the +U parameter (U), Fe–Fe distance (\(a/\sqrt{2}\)) and the out-of-plane coordinate of Se (zSe). The overall trend is that nematicity is favored by (a) a larger U (interaction driven) and (b) larger \(a/\sqrt{2}\) and zSe. Compared with \(a/\sqrt{2}\), zSe appears as a more sensitive factor.

Fig. 5: The evolution of total energy and OP amplitude.
figure 5

a–c The total energy of the β (blue triangles) and γ (red stars) solutions; and d–f the OP amplitude \({\Delta }_{{E}_{{\rm{u}}}}\) (red stars) and \({\Delta }_{{B}_{1{\rm{g}}}}\) (blue triangles) of the ground state (γ solution) as a function of the the +U parameter (U), Fe–Fe distance (\(a/\sqrt{2}\)) and the out-of-plane coordinate of Se (zSe).

Full size image

Figure 6 summarizes the ground-state band evolution as we change the microscopic details. It is informative to observe how the nematic band structure deforms back to the symmetric one on the left side of the figure. During the process, the dxz–dxy gap along the M−Σy direction gradually closes. The linear crossing without hybridization forms in the end.

Fig. 6: Ground-state band evolution.
figure 6

Band structure as a function of a the +U parameter (U), b Fe–Fe distance (\(a/\sqrt{2}\)) and c the out-of-plane coordinate of Se (zSe).

Full size image

Key ingredients to obtain the nematic solutions

There are several important theoretical considerations underlying the calculations, which distinguish the present work, and also explain why the nematic solutions were not identified in previous DFT and DMFT calculations.

PM condition

Within the nematic phase, FeSe is experimentally a PM metal. LSDA or sGGA has been shown to result in a quasi-degenerate lowest-energy manifold with stripe magnetic ordering momenta (π, Q) and (Q, π) (0 < Q ≤ π/2)45,46. The real spin state of the nematic phase has no long-range order. Based on the LSDA (sGGA) results, one natural speculation is a cooperative PM state45,46, i.e. fluctuations within the lowest-energy manifold restore the time-reversal symmetry. To comply with the C4 rotation symmetry breaking, it additionally requires that the fluctuations spontaneously condense into either the (π, Q) or (Q, π) direction. Another possibility is that the LSDA (sGGA) manifold actually collapses into a quantum PM state47. In contrast to the previous spin-polarized calculations, the present work focuses on nonmagnetic calculations, without introducing any spin order. Practically, we employ GGA instead of sGGA. For a PM metal, this is considered as a reasonable starting point.

Interaction correction

We have employed either DFT+U correction17 or hybrid functional18 to upgrade the description of strong interactions associated with the Fe d-electrons from an orbital-independent mean field to an orbital-dependent potential, which is the key to capture the orbital-ordering instabilities. Successful applications of these corrections to iron-based superconductors were hindered by the observation that +U tends to increase the error of ordered spin moment in the magnetic phase, as already overestimated at the LSDA (sGGA) level. This problem is automatically avoided in our nonmagnetic calculation. A unified view of the +U correction and the hybrid functional under the PM condition is that they both tend to cancel the unphysical Hartree potential of an electron with itself, which represents one of the most conspicuous error in LDA (GGA), and is significant for a localized orbital.

Wavefunction preconditioning

For a correlated system like FeSe, the energy landscape could be rather complicated. In consequence, numerical minimization might be easily trapped to some local minimum points48,49,50. In particular, starting from an initial electron-density ρ0(r) that respects the full symmetry of the underlying lattice, the iteration can easily end at a ρGS(r) without symmetry breaking. Therefore, to probe potential symmetry breaking, it is demanded to purposely drag ρ0(r) away from the symmetric basin by preconditioning the initial trial wavefunctions {ψi(r)}. Other preconditioning approaches, e.g., imposing an initial density matrix for correlated orbitals, can serve the same goal49,50.

OP analysis

The electron-density change [δρβ/γ(r)] with respect to the symmetric solution as shown in Fig. 1(c, d) exhibits clear symmetry breaking patterns. δρβ(r) can be easily associated with the widely discussed ferro-orbital nematic order. It is known that this OP is Ising type, belonging to the 1D B1g irrep of the D4h point group. By inspecting the density matrix \({\tilde{n}}^{\alpha \beta }\) within the Fe 3d-orbital subspace, where α and β label the five 3d-orbitals of the Fe atom, we confirm that the most noticeable change is \({\tilde{n}}^{yz,yz}-{\tilde{n}}^{xz,xz}\,\ne\, 0\). The x, y axes are along the Fe–Fe bonds. Accordingly, the symmetry breaking OP can be written as:

$${\Delta }_{{B}_{1{\rm{g}}}}={\tilde{n}}^{yz,yz}-{\tilde{n}}^{xz,xz}.$$
(1)

Following the choice of the three group generators in ref. 51 [See also the inset of Fig. 1(c, d)], we list the transformation matrices (parities for \({\Delta }_{{B}_{1{\rm{g}}}}\)) in Table 1.

Table 1 Transformation matrices of the predicted OPs with respect to the three generators of the P4/nmm/\({\mathcal{T}}\cong {D}_{4{\rm{h}}}\) point group.
Full size table

δργ(r) in the form of high-rank multipoles is however unexpected. By inspecting \({\tilde{n}}^{\alpha \beta }\), a fraction of \({\Delta }_{{B}_{1{\rm{g}}}}\) is also present in the γ solution, but an even larger change is the emergence of nonvanishing off-diagonal terms: \({\tilde{n}}^{xz,xy}\simeq {\tilde{n}}^{yz,{x}^{2}-{y}^{2}}\) (and the complex conjugate, \({\tilde{n}}^{xy,xz}\simeq {\tilde{n}}^{{x}^{2}-{y}^{2},yz}\)). We define this orbital hybridization as a new OP:

$${\Delta }_{{E}_{{\rm{u}},1}}={\tilde{n}}^{xz,xy}+{\tilde{n}}^{yz,{x}^{2}-{y}^{2}}.$$
(2)

This is not an Ising OP, which can be most clearly seen by rotating Fig. 1(c, d) by 90°. While Fig. 1(c) simply changes the sign, Fig. 1(d) is transformed into an inequivalent orientation. Formally, the other symmetry-related OP is obtained by interchanging x and y:

$${\Delta }_{{E}_{{\rm{u}},2}}={\tilde{n}}^{yz,xy}-{\tilde{n}}^{xz,{x}^{2}-{y}^{2}}.$$
(3)

These two OPs form a 2D Eu irrep. We list in Table 1 the associated transformation matrices.

It is interesting to note that the combination of the two terms in Eqs. (2) and (3) leads to an analytically compact form of electron-density modulation around Fe atoms:

$$\begin{array}{*{20}{l}}\delta {\tilde{\rho }}_{{E}_{{\rm{u}},1}}({\bf{r}})={\Delta }_{{E}_{{\rm{u}},1}}[{\psi }_{xz}({\bf{r}}){\psi }_{xy}({\bf{r}})+{\psi }_{yz}({\bf{r}}){\psi }_{{x}^{2}-{y}^{2}}({\bf{r}})]\\ \sim \,{R}_{3d}^{2}(r)\ {\sin }^{3}\theta \ \cos \theta \ \sin 3\phi \\ \sim \,{Y}_{4}^{3}(\theta ,\phi )+{Y}_{4}^{-3}(\theta ,\phi ),\end{array}$$
(4)

in which R3d(r) is the radial wavefunction of 3d-orbitals and (θ, ϕ) is the angular coordination of r. Similarly,

$$\delta {\tilde{\rho }}_{{E}_{{\rm{u}},2}}({\bf{r}}) \sim \,{Y}_{4}^{3}(\theta ,\phi )-{Y}_{4}^{-3}(\theta ,\phi ).$$
(5)

It is straightforward to check that the analytical \(\delta {\tilde{\rho }}_{{E}_{{\rm{u}},1}}({\bf{r}})\) indeed reproduces the overall geometry of δργ [Fig. 1(d)]. It can be viewed as a hexadecapolar order.

According to Fig. 5(d–f), \({\Delta }_{{E}_{{\rm{u}}}}\) and \({\Delta }_{{B}_{1{\rm{g}}}}\) typically coexist in the ground state, but \({\Delta }_{{E}_{{\rm{u}}}}\) is the leading one. The existence of the Eu OPs will generically generate the B1g order parameter, due to the symmetry-allowed coupling \({\Delta }_{{B}_{1{\rm{g}}}}({\Delta }_{{E}_{{\rm{u}},1}}^{2}-{\Delta }_{{{E}}_{{\rm{u}},2}}^{2})\) in an effective Ginzburg-Landau-type theory. The pure \({\Delta }_{{B}_{1{\rm{g}}}}\) (β solution) always has a higher energy.

Experimental consequences

Band reconstructions

Identification of the OPs reveal the physical origin of band reconstructions shown in Fig. 3. According to Table 1, both \({\Delta }_{{B}_{1{\rm{g}}}}\) and \({\Delta }_{{E}_{{\rm{u}}}}\) breaks \(\{{\sigma }_{{\rm{v}}}| \frac{1}{2}\frac{1}{2}\}\times {\sigma }_{{\rm{d}}}\), and thus the C4 rotation, leading to nematicity. The hole band splitting is primarily associated with this symmetry breaking, and the β and γ solutions behave similarly. The “hidden order” in \({\Delta }_{{E}_{{\rm{u}}}}\) is related to the further breaking of \(\{{\sigma }_{{\rm{v}}}| \frac{1}{2}\frac{1}{2}\}\). The remaining symmetry shrinks to a C2v group. We list in Table 2 the little groups of the three solutions. It is important to notice that \({\Delta }_{{B}_{1{\rm{g}}}}\) does not lower the symmetry of the ordinary k-points along Σx(y) directions. However, \({\Delta }_{{E}_{{\rm{u}}}}\) lowers the symmetry along Σy from C2v to Cs. The missing group element \(\{{\sigma }_{{\rm{v}}}| \frac{1}{2}\frac{1}{2}\}\) originally protects the dxz and dxy band crossing near the M point. This symmetry reason naturally explains why the “one-sided” gapping occurs, without the requirement of band inversion37 or orbital-selective quasiparticle weight43,44 as previously proposed. From a different angle, the “one-sided” gapping can be understood from the first term on the right hand side of Eq. (2). This hybridization term tends to mix dxz and dxy bands. On the other hand, dyz is coupled to d\({}_{{x}^{2}-{y}^{2}}\) only, which lies away from the Fermi surface. The crossing point between dyz and dxy bands is thus largely unperturbed. The redistribution of electron population between the dxz, dyz, and dxy orbitals below Ts was recently noticed in experiment52.

Table 2 Point groups of the three solutions at Γ and along Σx(y) directions.
Full size table

Inversion symmetry breaking

Another important difference between the C2v and the D2h point group is that C2v does not contain inversion symmetry. Direct measurement sensitive to electronic inversion symmetry breaking is now possible, thanks to the second harmonic generation (SHG) technique53,54,55. The prediction is that if the \({\Delta }_{{E}_{{\rm{u}},1(2)}}\) OP occurs, an unambiguous SHG signal should be observed below Ts. \({\Delta }_{{E}_{{\rm{u}},1(2)}}\) is conjugate to an in-plane electric field E along one of the Fe–Fe bonding directions. This will lead to a Dresselhaus splitting ~(E × k) ⋅ S, in which S is the electron spin operator. The splitting is largest along the k-direction perpendicular to E, and vanishes when k∥E. This term also leads to an out-of-plane polarization of the Fe spins, which is consistent with the spin-polarized inelastic neutron scattering data16. We quantify the Dresselhaus splitting by acting spin-orbit coupling (SOC) upon the PM γ solution as a first-order perturbation. Due to the overestimated band width, the SOC effect can be barely observed in Fig. 7(a), but a zoomed-in view [Fig. 7(b)] clearly shows the directional splitting of the order of O(10) meV. This is also considered as a signature of \({\Delta }_{{E}_{{\rm{u}}}}\), which can in principle be resolved in high-precision ARPES data, e.g., ref. 56, and the Supplementary material of ref. 34. In the same way as \({\Delta }_{{B}_{1{\rm{g}}}}\) couples to a shear strain of the lattice7, \({\Delta }_{{E}_{{\rm{u}}}}\) couples to a special type of structural distortion. According to the full relaxation at the hybrid functional level, a relative glide between the Fe and Se layers occurs along one of the Fe–Fe bonding directions, which also breaks the inversion symmetry in analogy to the polar distortion in ferroelectric materials. However, the calculated magnitude is as small as 0.001 Å, which again reflects that lattice instability is not the driving force.

Fig. 7: The effect of SOC.
figure 7

a Ground-state (γ solution) band structure including SOC; b directional Dresselhaus splitting around the electron pocket.

Full size image

Pressure effect

The band evolution under reduced in-plane lattice constant and the out-of-plane distance between the Fe and Se layers (Fig. 6b, c) can be regarded as an examination of the pressure effect. Our results are consistent with the experimental observation of a strong reduction of the nematic transition temperature under pressure20. According to the experimental phase diagram20, while the nematic phase is suppressed, the stripe antiferromagnetic phase emerges. This instability is not covered in the present nonmagnetic framework. It is believed that a quantum phase transition occurs along the pressure axis. Beyond a critical point, the PM condition no longer applies.

Perspective

In summary, we demonstrated a first-principle approach to reproduce the PM nematic state in FeSe, without breaking either the tetragonal lattice symmetry or the time-reversal symmetry. We incorporated orbital-resolved interactions by +U and hybrid functional, and preconditioned the initial wavefunction to find self-consistent solutions with spontaneous symmetry breaking. The lowest-energy nematic state we found features a two-component vector OP belonging to the Eu irrep, in addition to the Ising ferro-orbital order, which is important to produce the correct Fermi surface topology. We proposed that the inversion symmetry breaking induced by the Eu OP could be detected by high-precision measurement of the band dispersion as well as SHG. For the closely related material FeTe, a SHG experiment has already been reported, observing anomalies across the symmetry-breaking transition55.

From the computational side, it is worth further investigation to generalize the present nematic solutions to more advanced first-principle methods with interaction corrections beyond the Hartree–Fock level. If one views the +U correction as the simplest DMFT with a static onsite self energy57, it is reasonable to expect that a more accurate treatment of the onsite correlation via a quantum impurity solver should better reproduce the experiment. Technically, the main issue is how to precondition the initial Green’s function. If the conventional construction out of the converged LDA (GGA) Hamiltonian cannot automatically guide the DFT-DMFT loops to the nematic solutions, some alternative starting points have to be chosen. Similarly, if one views the GW method as a dynamical hybrid functional58, it is reasonable to expect that DFT + GW is also sufficient to reproduce nematicity in FeSe.

Methods

Rountine setup

All the presented calculation results are obtained by using the Vienna ab initio Simulation Package (VASP)59. The lattice structure respects the full P4/nmm space group symmetry throughout the DFT+U study. The experimental lattice parameters of bulk FeSe60 are used as the reference to obtain the main results. As a benchmark, we also perform full structural relaxation using the HSE0661,62 hybrid functional. The atomic positions are relaxed until the residual forces are smaller than 5 × 10−3 eV Å−1. In the end, the in-plane lattice constant and the Se height are manually varied separately to understand their effects.

The plane-wave cutoff is 500 eV in combination with the projector augmented wave method63. The Monkhorst-Pack64 k-point grid is 12 × 12 × 6. The exchange and correlation is treated by using the Perdew–Burke–Ernzerhof GGA functional65. The convergence criteria is 10−6 eV for electronic iterations. The automatic symmetrization routine is switched off to probe electronic spontaneous symmetry breaking.

Unless specified otherwise, the presented calculation results include the rotational invariant +U correction introduced by Dudarev et al.66 with U = 3.6 eV (or more rigorously, U–J = 3.6 eV). The more complicated orbital-dependent +U correction as introduced by Liechtenstein et al.67 with U = F0 = 4.8 eV and J = (F2 + F4)/14 = 1.2 eV and F2/F4 = 0.625 gives very similar results. This +U parameter is selected by benchmarking the band structure to HSE06 hybrid functional results, which contains no material-specific parameter. In the end, we purposely tune Dudarev’s +U parameter from 3.2 to 4.0 eV to understand its effect on the results.

Wavefunction preconditioning

To target the lowest-energy solution, various initial wavefunctions for the DFT iteration are tested. We first generate a set of ψi(r) from a preparatory calculation on a manually distorted FeSe lattice that slightly breaks the symmetry. Then this set of {ψi(r)} is fed to an undistorted FeSe lattice as a starting point to see whether it flows to a different local minimum. No matter how the preconditioning is performed, the energy landscape for the production run does not change, and is always ensured to be an invariant of the space group P4/nmm. Specifically, we find that preconditioned wavefunctions generated by an uniaxial strain along the x (or equally y) axis (see the inset of Fig. 1 for the definition of the x-axis) tend to flow into the β basin. For the γ solution, the most convenient preconditioning is to shift the origin of the Fe layer along either the x or the y axis. We have tested wavefunction preconditioning associated with all the zone-center optical phonon modes (with VASP), as well as imposing the initial density matrix of the Fe 3d-orbitals (with the ABINIT code50,68,69) to cover all the ten irreps of the D4h point group, which confirm that the γ solution has the lowest energy. Certain minimization algorithms70 are able to escape shallow local minima. We find that without preconditioning, the damped velocity friction algorithm (See for example Sec. III of70) can still correctly find the γ solution as the ground state, despite a significantly larger number of iterations.

Validity and limitations

For the electronic structure above the nematic transition temperature (Ts ~ 90 K for FeSe), LDA (GGA) instead of LSDA (sGGA) is the common choice to construct the tight-binding model (See, for example, Chpt. 8 in ref. 1). Across Ts, the PM condition of the metallic state does not significantly change19,71. Despite an oversimplified description of paramagnetism, we consider that the symmetric LDA (GGA) band structure is eligible to serve as the numerical parent state, upon which we test whether the residual interaction effects drive any orbital instability at the Hartree–Fock level.

The main limitation of our calculation is the missing of dynamical spin fluctuation and short-range antiferromagnetic correlation. A traditional DFT approach to describe high-temperature PM states is to perform random average of different magnetically ordered states under LSDA (sGGA). However, the low-temperature quantum paramagnetism in FeSe has a much more complicated nature. Without an accurate knowledge of the spin ground state, the average is problematic. A perspective on generalizing the present calculation to more advanced algorithms is discussed in the end of the main context.