Introduction

The electrical conductivity of a metal σ and its thermal counterpart κ are linked to each other by the Wiedemann–Franz (WF) law, provided that the heat carried by phonons is negligible and electrons do not suffer inelastic scattering. This law states that the ratio of the two conductivities divided by temperature should be equal to a universal number set by fundamental constants. The validity of the WF law is expected both at very low temperatures, where elastic scattering by disorder dominates, and above the Debye temperature, where scattering by phonons becomes effectively elastic. At intermediate temperatures, inelastic scattering is known to degrade thermal current more efficiently than the electrical current.1 Experiments have found a zero-temperature validity combined to a downward departure in elemental metals (due to electron–phonon scattering)2,3 as well as in correlated metals (because of electron–electron scattering).4,5 During the past decade, the search for a possible breakdown of the WF law near a quantum critical point6 motivated high-resolution experiments, which verified its zero-temperature validity within experimental margin and quantified the deviation at finite temperature.7,8,9,10

Gooth et al.11 have recently reported on thermal transport in micrometric samples of WP2 down to 5 K and found a drastic breakdown of the WF law. WP2 is a type-II Weyl semimetal with a room-temperature residual resistivity ratio (RRR) expressed in five digits and an impressively large magnetoresistance.12 The observation raised fundamental questions regarding the relevance of the scattering-based theory of charge and entropy transport by mobile electrons to this non-trivial solid. The possible link between WF breakdown and electron hydrodynamics is a subject of attention.13,14,15,16,17

In this paper, we present a study of thermal conductivity in bulk millimetric single crystals of WP2. By performing concomitant measurements of thermal and electrical transport between 2 and 40 K, we find that: (i) The WF law is obeyed at 2 K, but a drastic downward deviation of exceptional amplitude emerges at higher temperatures; (ii) Thanks to the low-temperature data, one can distinguish between the contributions to the thermal and electrical resistivities arising from electron–electron and electron–phonon scattering; (iii) The downward deviation arises because of a large (fivefold) difference between the amplitudes of the T-square prefactors in the two (electrical and thermal) resistivities due to electron–electron scattering. We conclude that electron–electron scattering is the origin of the exceptionally large downward deviation from the Wiedemann–Franz law. This can happen if small-angle momentum-relaxing scattering events are unusually frequent. Thus, the semi-classical transport theory is able to explain a large mismatch between Lorenz number and Sommerfeld number at finite temperature. However, the large T-square thermal resistivity caused by momentum-conserving scattering among electrons, together with the long mean-free-path of the electrons, opens a window for entering into the hydrodynamic regime.

Results

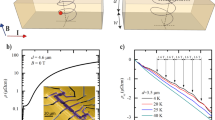
Figure 1a shows the resistivity as a function of temperature in a WP2 single crystal. The RRR for this sample is ρ(300K)/ρ(2K) = 9600. The residual resistivity ρ0 of the different samples was found to lie between 4 and 6 nΩ cm. With a carrier density of 2.5 × 1021 cm−3,11 this implies a mean-free-path in the range of 70 to 140 μm, and, given the dimensions of the sample, a proximity to the ballistic limit.

Fig. 1
figure 1

a Resistivity of WP2, ρ, measured along the a-axis, as a function of temperature. b Thermal conductivity divided by temperature, \({\textstyle{\kappa \over T}}\) (jQ//a-axis) as a function of temperature in the same sample with the same electrodes. c Ratio of Lorenz, \(L(T) = {\textstyle{\kappa \over {T\sigma }}}\) to Sommerfeld L0 = 2.44 × 10−8 W Ω K−2, numbers as a function of temperature (red). The data reported for a micro-ribbon of WP211 are shown in green. d L(T)/L0 as a function of temperature in CeRhIn5.4 e L(T)/L0 as a function of temperature for an Ag wire with a 50 μm diameter and 99.99% purity. WP2 and Ag were measured with the same experimental set-up. Error bars are due to the error on the measurement of the resistance of the thermometers, which are used to evaluate the temperature gradient in the sample

Full size image

The temperature dependence of κ/T, the thermal conductivity divided by temperature, is plotted in panel (b) of the Fig. 1. Note that in our whole temperature range of study, the phonon contribution to heat transport is negligible (see Supplemental Material). The extracted Lorenz number, \(L(T) = {\textstyle{{\kappa \rho } \over T}}\), is to be compared with the Sommerfeld number \(L_0 = {\textstyle{{\pi ^2} \over 3}}\left( {{\textstyle{{k_B} \over e}}} \right)^2\). As seen in Fig. 1c, according to our data, L/L0 is close to 0.5 at 40 K and decreases with decreasing temperature until it becomes as low as 0.25 at 13 K, in qualitative agreement with the observation originally reported by Gooth et al.,11 who first reported on a very low magnitude of the L/L0 ratio in WP2. As seen in the Fig. 1c, however, the two sets of data diverge at low temperature and we recover the expected equality between L and L0 at low temperature.

Comparison with two other metals, Ag and CeRhIn5, is instructive. Figure 1d displays the temperature dependence of L/L0 in the heavy-fermion antiferromagnet, CeRhIn5 as reported by Paglione et al.4 The L/L0 ratio, close to unity at 8 K, decreases with decreasing temperature and becomes as low as 0.5 at 2 K, before shooting upwards and attaining unity around 100 mK. In Ag, as seen in Fig. 1e, which presents our data obtained on a silver wire, a similar downward deviation of the L/L0 ratio is detectable. Close to unity below 8 K, it decreases with warming and attains a minimum of 0.6 at 30 K before increasing again.

It is also instructive to recall the case of semi-metallic bismuth, in which thermal transport is dominated by phonons. In such a compensated system, an ambipolar contribution to the thermal conductivity, arising from a counter-flow of heat-carrying electrons and holes, was expected to be present.18,19 An ambipolar diffusion would have led to an upward deviation of L/L0 from unity. However, Uher and Goldsmid18 found (after subtracting the lattice contribution) that L/L0 < 1 in bismuth, which indicates that there is no ambipolar contribution to the thermal conductivity. The absence of a significant phononic contribution in our data makes the interpretation even more straightforward, and we also find no evidence for ambipolar heat transport in WP2. The reason is that the electron and hole gases are degenerate both in Bi (below room-temperature) and WP2 (for all temperatures of interest), and thus the ambipolar contribution is small in proportion to T/EF.

The scattering-based Boltzmann picture provides an explanation for such downward deviations. Thermal and electrical transport are affected in different ways by inelastic collisions labeled as “horizontal” and “vertical” (See Fig. 2a). In a horizontal scattering event, the change in the energy of the scattered carrier is accompanied by a drastic change of its momentum. Such a large-q process degrades both charge and heat currents. A vertical process, on the other hand, is a small-q scattering event, which marginally affects the carrier momentum, but modifies its energy as strongly as a horizontal process of similar intensity. In the case of momentum transport, the presence of a (1 − cos θ) pondering factor disfavors small-angle scattering. No such term exists for energy transport. This unequal importance of vertical events for electrical and thermal conductivities, pulls down the L(T)/L0 ratio at finite temperature and generates a finite temperature breakdown of the Wiedemann–Franz law.1 Such a behavior was observed in high-purity Cu half a century ago,2 in other elements, such as Al and Zn,3 in heavy-fermion metals such as UPt3,5 CeRhIn54 or CeCoIn57 as well as in magnetically ordered elements like Ni20 or Co.21

Fig. 2
figure 2

a A schematic representation highlighting the difference between horizontal and vertical inelastic scattering. Both kind of processes degrade heat transport. Their effect on momentum transport is, however, very different. Arrows indicate scattering from one state to another. b A sketch of Normal and Umklapp scattering in the case of a simple circular Fermi surface (blue), inside a rectangular Brillouin zone (red). They differ by the balance of quasi-momentum exchange after collision. \(\vec dQ = \vec k_{2f} + \vec k_{1f} - \vec k_{2i} - \vec k_{1i}\) is zero in a normal process and equal to a unit vector of the reciprocal lattice in an Umklapp one

Full size image

On the microscopic level, two distinct types of vertical scattering have been identified. The first is electron–phonon scattering,1 relevant in elemental metals. At low-temperatures, the Bloch-Grüneisen picture of electron–phonon scattering yields a T5 electric resistivity and a T3 thermal resistivity. The higher exponent for charge transport is due to the variation of the typical wave-vector of the thermally excited phonons with temperature: \(q_{ph} = {\textstyle{{k_BT} \over {\hbar v_s}}}\). Small-angle phonon scattering becomes more frequent with cooling. Therefore, phonons’ capacity to degrade a momentum current declines faster than their ability to impede energy transport. This power law difference leads to L(T)/L0 < 1 in the intermediate temperature window (below the Debye temperature), when phonon scattering dominates over impurity scattering, but all phonons are not thermally excited. A second source of q-selectivity concerns momentum-relaxing electron–electron scattering (See Fig. 2b). The quadratic temperature dependence of resistivity in a Fermi liquid is a manifestation of such scattering.22 This is because the phase space for collision between two fermionic quasi-particles scales with the square of temperature. Since the total momentum before and after collision is conserved, electron–electron collisions degrade the flow of momentum only when the scattering is accompanied by losing part of the total momentum to the lattice. Two known ways for such a momentum transfer are often invoked.23 The first is Baber mechanism, in which electrons exchanging momentum belong to two distinct reservoirs and have different masses. The second is an Umklapp process, where the change in the momentum of the colliding electrons is accompanied by the loss of one reciprocal lattice wave-vector (Fig. 2b). Abundant small-angle electron–electron scattering (which could be either Umklapp or Baber-like) would generate a mismatch in prefactors of the T-square resistivities with the electrical prefactor lower than the thermal one. This is a second route towards L(T)/L0 < 1, prominent in correlated metals.24,25

In order to determine what set of microscopic collisions causes the downward deviation from the WF law in WP2, we identified and quantified various contributions to the thermal and electrical resistivities of the system.

Figure 3 shows the electrical resistivity, ρ, and thermal resistivity, WT, as a function of T2. In order to keep the two resistivities in the same units and comparable to each other, we define \(WT = {\textstyle{{TL_0} \over \kappa }}\), as in ref. 4. One can see that at low temperatures, the temperature-induced increase in ρ and WT is linear in T2, confirming the presence of a T-square component in both quantities. The intercept is equal in both plots, which means that the WF law is valid in the zero-temperature limit. But the two slopes are different and the deviation from the low-temperature quadratic behavior occurs at different temperatures and in different fashions.

Fig. 3
figure 3

a Electrical resistivity, ρ, as a function of T2. The dotted line is a linear fit to the T < 10 K data. The inset shows δρ = ρ − ρ0 − AT2 as a function of T5 expressed in nΩ cm. b Thermal resistivity, \(WT = {\textstyle{{L_0T} \over \kappa }}\), as a function of T2. The dotted line is a linear fit to the T < 8 K data. The inset shows δWT = WT − W0T − BT2 as a function of T3 expressed in nΩ cm

Full size image

Discussion

Admitting three distinct contributions (scattering by defects, electrons and phonons) to the electrical and thermal resistivities, the expressions for ρ and WT become:

$$\rho = \rho _0 + A_2T^2 + A_5T^5$$
(1)
$$WT = W_0T + B_2T^2 + B_3T^3$$
(2)

We assume these scattering mechanisms to be additive. Note that since the data are limited to a temperature window in which \(T > {\textstyle{\hbar \over {k_B\tau }}}\), no Altshuler-Aronov corrections are expected.26 As seen above, ρ0 = W0T, but A2 ≠ B2. The insets in Fig. 3 show that ρ − ρ0 − A2T2 is linear in T5 and WT − W0T − B2T2 is proportional to T3, in agreement with what is expected from Eqs. (1) and (2).

It is now instructive to compare WP2 and Ag to examine the possible role played by inelastic phonon scattering. Figure 4 compares the amplitude of the T5 terms in WP2 and Ag. As seen in the Fig. 4, the amplitude of both A5 and B3 is larger in WP2. More quantitatively, A5(WP2)/A5(Ag) = 3.4 and B3(WP2)/B3(Ag) = 3.6. In other words, the B3 and A5 ratios of WP2 and Ag are similar in magnitude, which implies that phonon scattering is not the origin of the unusually low magnitude of the Lorenz number in WP2.

Fig. 4
figure 4

a Inelastic electrical resistivity δρ caused by phonon scattering in WP2 (black) and Ag (red) as a function of T5. b Inelastic thermal resistivity, δWT, in WP2 (black) and Ag (red) as a function of T3. The ratio of the two slopes is similar for heat and charge transport

Full size image

Having ruled out a major role played by phonon scattering in setting the low magnitude of L/L0, let us turn our attention to electron–electron scattering. As stated above, the prefactors of the T-square terms in ρ and WT, namely A2 and B2, are unequal. The ratio A2/B2 is as low as 0.22, well below what was observed in other metals, such as CeRhIn5 (A2/B2 ≃ 0.4),4 UPt3 (A2/B2 ≃ 0.65),5 or nickel (A2/B2 ≃ 0.4).20 This feature, which pulls down the magnitude of the L/L0 ratio in WP2, may be due to unusually abundant vertical events (involving a small change in the wave-vector of one of the colliding electrons), which could be either Umklapp or inter-band involving collisions between hole-like and electron-like carriers belonging to different pockets.

To have electron–electron collisions, which are simultaneously small-angle, Umklapp, and intra-band, one needs a Fermi surface component located at the zone boundary.27 Interestingly, as seen in Fig. 5, this is the case of WP2. The figure shows the Fermi surface obtained by our Density Functional Theory (DFT) calculations (see Supplemental Material), consistent with previous reports.28,29 It is composed of two hole-like and two electron-like pockets, each located at the boundary of the Brillouin zone. Such a configuration allows abundant intra-band low-q Umklapp scattering. According to previous theoretical calculations,24,25 the weight of small-angle scattering can pull down the A2/B2 (and the L/L0) ratio. However, the lowest number found by these theories (≃0.38) is well above what was found here by our experiment on WP2 (A2/B2 ≃ 0.22), as well as what was reported long ago in the case of tungsten30 (see Supplemental Material).

Fig. 5
figure 5

a DFT-computed 3D Fermi Surface of WP2. b Top view of the Fermi surface. Arrows illustrate wave-vectors during an inter-band Umklapp and small-angle scattering event. \(\vec k_{i,n}\) and \(\vec k_{f,n}\) are carrier momenta, \(\vec k_{f,2} - \vec k_{i,2} = \vec q\) and \(\vec k_{f,1} - \vec k_{i,1} = \vec G + \vec q\)

Full size image

Following the present experimental observation, Li and Maslov showed31 that in a compensated metal with a long-range Coulomb interaction among the charge carriers, the Lorenz ratio is given by

$$L{\mathrm{/}}L_0 = \left( {\kappa {\mathrm{/}}k_{\mathrm{F}}} \right)^2{\mathrm{/}}2$$
(3)

where κ is the (inverse) screening length and kF is the (common) Fermi momentum of the electron and hole pockets. By assumption, \(\kappa \ll k_{\mathrm{F}}\) and thus L/L0 can be arbitrarily small in this model.

Let us now turn our attention to the possibility that WP2 enters the hydrodynamic regime.11 In order to address this question, let us first recall what is known in the case of normal-liquid 3He. The latter presents a thermal conductivity inversely proportional to temperature32 (strictly equivalent to our WT being proportional to T2) and a viscosity proportional to T−233 at very low temperatures. Both features are caused by fermion-fermion collisions,34 which are normal and conserve total momentum. As one can see in Fig. 6, the magnitude of B2 (prefactor of the thermal T-square resistivity) in 3He, in CeRhIn5, in WP2 and in W plotted vs. γ, the fermionic specific heat, lies close to the universal Kadowaki–Woods plot. This means that while A2 quantifies the size of momentum-relaxing collisions and B2 is a measure of energy-relaxing, yet momentum-conserving collisions, both scale roughly with the size of the phase space for fermion-fermion scattering, which (provided a constant fermion density) is set by γ2. As a consequence, the magnitude of B2 opens a new window to determine where one may expect electron hydrodynamics.

Fig. 6
figure 6

a The Kadowaki–Woods plot with A2 and B2 plotted as a function of fermionic specific heat γ (C = γT). To the plot compiled by Tsujii et al.,43 we have added the data for 3He,32,44,45 WP2 (this work), W30 and CeRhIn5.4,46 These compounds are indicated by boxes

Full size image

The hydrodynamic regime35,36 of electronic transport (identified long ago by Gurzhi37) requires a specific hierarchy of scattering times. Momentum-conserving collisions should be more frequent than boundary scattering and the latter more abundant than momentum-relaxing collisions. Let us show that this hierarchy can be satisfied in our system thanks to the combination of an unusually low A2/B2 ratio and low disorder. The combination of a residual resistivity as low as 4 nΩ cm and a carrier density of 2.5 × 1021 cm−3 according to11 (compared to 2.9 × 1021 cm−3 according to our DFT calculations) implies that we are at the onset of the ballistic limit. It yields a mean-free-path of 140 μm. This is to be compared to the sample width and thickness of 0.1 mm.

Like in many other cases,38 the Dingle temperature of quantum oscillations yields a mean-free-path much shorter than this. A particularly large discrepancy between the Dingle and transport mobilities has been observed in low-density semi-metals such as Sb.39 In the system under study, the difference is as large as three orders of magnitude.12 This is presumably because of a very long screening length, weakening large-angle scattering, and helping momentum conservation along long distances.

This feature, combined with the fact that momentum-conserving collisions are 4–5 times more frequent than momentum-relaxing ones, implies that the system satisfies the required hierarchy of scattering times in a limited temperature window, as one can seen in Fig. 7. This figure compares the temperature dependence of momentum-relaxing collisions (with other electrons and phonons), momentum-conserving collisions (among electrons) and the boundary scattering. The three terms are represented by their contributions to resistivity, convertible to scattering rates by the same material-dependent factor. Note the narrowness of the temperature window and the modesty of the difference between the three scattering rates. Note, also that the hydrodynamic regime coincides with the observed minimum in L/L0 representing an excess of momentum flow in comparison to energy flow. In the hydrodynamic scenario, this coincidence is not an accident. However, the position and the width of this window are not solidly set. Assuming that the residual resistivity is not entirely fixed by the boundary scattering (i.e., ρ0 = ρ00 + ρimp) would shift this temperature window and beyond a threshold ρimp, the window will close up (see Supplemental Material).

Fig. 7
figure 7

The magnitude of B2T2, proportional to momentum-conserving (MC) electron–electron collisions is compared to ρimp + A2T2 + A5T5, which is proportional to momentum-relaxing (MR) collisions by electrons and phonons and ρ0, which is a measure of boundary scattering. In a limited temperature window (7 < T < 13 K), the hierarchy for hydrodynamic regime is satisfied

Full size image

In purely hydrodynamic transport, momentum relaxation occurs only at the boundary of the system. Momentum-conserving collisions then set the magnitude of the viscosity and the fluid drifts in presence of an external force. However, this does not happen in WP2 or in any other metal, because the finite B2/A2 ratio means that momentum-relaxing events are not absent. In our hydrodynamic regime, an electron traveling from one end of the sample to the other suffers few collisions and four-out-of-five of them conserve momentum. Because the three scattering times (momentum-conserving, momentum-relaxing and boundary) are of the same order of magnitude, any hydrodynamic signature would lead to modest corrections to what can be described in the diffusive or ballistic regimes, such as subtle departures in size-dependent transport properties.36

One message of this study is that a finite temperature departure from the WF law by itself cannot be a signature of hydrodynamic transport, but thermal transport can be used to quantify the relative weight of momentum-conserving collisions and to identify where to expect eventual hydrodynamic features. Specifically, our study highlights two features, which were not explicitly considered in previous discussions about the hydrodynamics of electrons. First, as for phonons,40 the hydrodynamic regime for electrons is expected to occur in a finite temperature window squeezed between the ballistic and diffusive regimes. Second, the phase spaces for momentum-relaxing and momentum-conserving collisions for electrons follow the same (T-square) temperature dependence. This is in a contrast to the case of phonons where Umklapp scattering vanishes exponentially with temperature whereas normal scattering follows a power law.41 This difference makes electron hydrodynamics more elusive in comparison with its phononic counterpart.42

We note also that the two solids showing anomalously low L/L0 (W and WP2) are those in which the T = 0 ballistic limit is accessible and a hydrodynamic window can open up. Future studies on samples with different dimensions11 using a four-contact measurement set-up are necessary to reach a definite conclusion.

In summary, we found that WP2 obeys the Wiedemann–Franz law at 2 K, but there is a large downward deviation, which emerges at higher temperatures. We recalled that the dichotomy between charge and heat transport is ubiquitous in metallic systems, since low-q scattering affects heat conduction more drastically than charge transport. The exceptionally low magnitude of L/L0 ratio mirrors the discrepancy between the amplitude of T-square prefactors in thermal and electrical resistivities. The large difference between momentum-conserving and momentum-relaxing collisions among electrons opens a narrow temperature window where the hierarchy of scattering times conforms to hydrodynamic requirements.

Methods

The samples used in this study were needle-like single crystals (grown along the a-axis). Their typical dimensions were 1–2 × 0.1 × 0.1 mm3. The samples are similar to those detailed in ref. 12 they were grown by chemical vapor transport. Starting materials were red phosphorous (Alfa-Aesar, 99.999%) and tungsten trioxide (Alfa-Aesar, 99.998%) with iodine as a transport agent. The materials were taken in an evacuated fused silica ampoule. The transport reaction was carried out in a two-zone-furnace with a temperature gradient of 1000 °C (T1) to 900 °C (T2) for several weeks. After reaction, the ampoule was removed from the furnace and quenched in water. The metallic needle-like crystals were later characterized by X-ray diffraction. The measurements were performed with a standard one-heater-two-thermometers set-up, with Cernox chips, allowing to measure thermal conductivity κ and the electrical resistivity ρ with the same electrodes and the same geometrical factor. Contacts were made with 25 μm Pt wires connected via silver paste with a contact resistance ranging from 1 to 10 Ω. The electric and heat currents were injected along the a-axis of the sample. By studying three different samples with different RRRs, we checked the reproducibility of our results (see the Supplemental Material).