Giant spin-valley polarization and multiple Hall effect in functionalized bismuth monolayers

Abstract

Valleytronic materials, characterized by local extrema (valleys) in their bands, and topological insulators have separately attracted great interest recently. However, the interplay between valleytronic and topological properties in one single system, likely to enable important unexplored phenomena and applications, has been largely overlooked so far. Here, by combining a tight-binding model with first-principles calculations, we find the large-band-gap quantum spin Hall effects (QSHEs) and valley Hall effects appear simultaneously in the bismuth monolayers decorated with hydrogen/halogen elements, denoted as Bi₂XY (X, Y = H, F, Cl, Br, or I). A staggered exchange field is introduced into the Bi₂XY monolayers by transition-metal atom (Cr, Mo, or W) doping or LaFeO₃ magnetic substrates, which together with the strong spin-orbit coupling of bismuth atoms generates a time-reversal-symmetry-broken QSHE and a huge valley splitting (up to 513 meV) in the system. With gate control, QSHE and anomalous charge, spin, valley Hall effects can be observed in the single system. These predicted multiple and exotic Hall effects, associated with various degrees of freedom of electrons, could enable applications of the functionalized bismuth monolayers in electronics, spintronics, and valleytronics.

Introduction

Tailoring valley degrees of freedom offers fascinating opportunities to realize novel phenomena and emerging applications, often referred to as valleytronics.^1,2,3,4 While valley effects have been studied for decades in materials such as silicon,⁵ diamond,⁶ AlAs,⁷ and graphene,^8,9,10,11 despite the effort to emulate the better known manipulation of spin and spintronic applications,¹² the related success has been modest.² Often the progress in harnessing the valley degrees of freedom was limited not by the lack of ideas,¹³ but by the material properties, including the small valley polarization and a weak spin-orbit coupling (SOC) inherent to graphene.^1,8,11 The resurgence of interest in valley effects was recently spurred by the discovery of monolayer (ML) transition-metal dichalcogenides (TMDs) with broken inversion symmetry and strong SOC.^{14,15,16,17,18,19,20,21,22} A hallmark of ML TMDs is their valley-spin coupling, which leads to a valley-dependent helicity of optical transitions^23,24,25 as well as important implications for transport, such as the discovery of the valley Hall effect (VHE).⁴ Lifting the degeneracy between the valleys K and K’ to generate the valley polarization was identified as the key step in manipulating valley pseudospin degrees of freedom.^{15,16,17,18,19,20,21,22} Common approaches were focused either on optical pumping by circularly polarized light^23,24,25 or very large magnetic fields required by a small Zeeman splitting of ~0.1 meV/T.^26,27 Instead of these external methods to realize valley polarization that could be impractical or limited by the carrier lifetime,³ transition-metal (TM) doping^16,17,18 or magnetic proximity effects^19,20,21,22 have been found effective ways to get permanent valley polarizations in TMDs. Since topological properties are very important for materials,¹ the coupling of the topological behavior and valley polarizations in the valleytronic materials may give rise to new physics and applications. However, the widely studied valley-polarized material TMDs have topologically trivial band gaps.^{16,17,18,19,20,21,22} The combination of topological and valleytronic has been rarely explored up to the present. It would be very interesting to search for such topologically nontrivial valleytronic materials and explore their valley-dependent transport properties.

Since the topological properties and transverse velocities of the electrons in the VHEs are closely related to the SOC strength of the system, it is desirable to search for and to explore the valley-related phenomenon in large SOC material systems. Very strong SOC can be generally induced in materials containing heavy elements, such as bismuth, and drives the appearance of the topologically nontrivial states in the Bi-related systems.^28,29 In experiments, the buckled ML structure of Bi (111) with a hexagonal lattice has been successfully synthesized and characterized.²⁸ A nontrivial quantum spin Hall effect (QSHE) band gap of 0.8 eV was observed experimentally in ML Bi on the top of a SiC substrate.²⁸ With the hydrogen (H),^30,31 halogens (F, Cl, Br, I)³¹ or methyl (CH₃)³² saturating p_z orbitals of Bi atoms, the buckled Bi (111) ML forms a hexagonal flat geometry Bi₂X₂ (X = H, F, Cl, Br, I, or CH₃), of which atomic structures are predicted to be stable at up to 600 K.³¹ A giant SOC strength, producing global nontrivial band gaps up to 1.03 eV, was reported in the Bi₂X₂ system.^31,32 These p_x and p_y orbital-induced large SOC should be beneficial for coupled spin and valley physics. Due to the presence of inversion symmetry in the crystal structure of Bi₂X₂, no valley-related phenomenon emerges in the previous work.^28,30,31,32

In this work, by focusing on strong SOC in ML Bi (111)-based systems, we use tight-binding (TB) model and ab-initio studies to demonstrate materials design of topological effects which rely on valley-dependent Berry curvature. Large nontrivial band gaps (from 0.891 eV to 1.256 eV) are obtained at the two valleys in ML Bi (111) with different chemical decorations on the two surfaces of the MLs, forming Bi₂XY (X, Y = H, F, Cl, Br, or I and X ≠ Y) structures, which provide a platform for fabricating the wide-frequency valley-light devices. To break the degeneracy of the K and K’ valleys, we induce a staggered exchange field ΔM = M_A – M_B into the ML Bi₂XY with the assumption of M_A > M_B, where M_A is the magnetic exchange field in the A sublattice of the ML Bi and M_B is the magnetic exchange field in the B sublattice. The TB model calculations show that when SOC is larger than both M_A and M_B, the time-reversal symmetry-broken (TRSB) QSH states and obvious spin-valley polarizations emerge in the system. With electron (hole) doping, the spin-down electrons (spin-up holes) produce a spin-valley polarized net transverse current, giving rise to spin-valley polarized anomalous valley Hall effects (AVHEs), also called anomalous charge/spin/valley Hall effects. Thus, with gate control, multiple Hall effects including QSHEs and anomalous charge/spin/valley Hall effects can be manipulated in the single system. To carry out these effects in experiments, we propose two possible schemes based on ab-initio calculations. (1) A functionalized ML Bi₂XY with transition-metal (TM = Cr, Mo, or W) atoms doped, in which the valley splitting can be giant, with a maximum value of 513 meV. (2) A heterostructure of ML Bi₂H deposited on a LaFeO₃ (111) surface, where a valley splitting is about 78 meV. The predicted multiple Hall effects associated with multiple degrees of freedom of electrons in functionalized ML Bi pave a brand new way to electronics, spintronics, and valleytronics of two-dimensional materials.

Results and discussion

The structure of ML Bi₂XY (X, Y = H, F, Cl, Br, or I) is shown in Fig. 1a, b, where the Bi atoms construct a quasi-planar honeycomb lattice, the X atoms bond the upper surface Bi atoms, and the Y atoms bond the lower surface Bi atoms. When X = Y, the Bi₂XY structures form the ML Bi₂X₂ (X = H, F, Cl, Br, or I), which has been predicted to be stable up to 600 K and show QSH effects.³¹ The ML Bi₂X₂ has inversion symmetry with point group of D_3d.³¹ The Bi p_z orbitals are saturated by the later added X atoms. The strong SOC from Bi p_x and p_y orbitals near the Fermi level (E_F), thus, opens large nontrivial band gaps at the K and K’ valleys.^30,31,32 The calculated local band gaps of Bi₂X₂ (X = H, F, Cl, Br, or I) are found in the range from 1.160 eV to 1.306 eV as shown in Supplementary Table S1 and Fig. S1 in Supplementary Information. A large SOC in the ML Bi₂X₂ could be employed for the potential valleytronic applications after the inversion symmetry of the system is broken.

Fig. 1

Geometry and band structures of functionalized Bi monolayers without magnetization. a Top and b side views of the structure of ML Bi₂XY (X, Y = H, F, Cl, Br, or I). c and d Energy bands for the ML Bi₂XY (X = Y) system from the TB model without and with SOC considered, respectively. e and f The same as c and d, respectively, except for X ≠ Y. The small red/blue arrow in c, d indicates the spin-up/spin-down state. The red/blue curve in f indicates the spin-up/spin-down state. The black dots in f denote the Berry curvatures for the whole valence bands. The TB parameters of t₁ = 0.8 eV, t₂ = 1.0 eV, 2U = 0.0/0.12 eV, λ_SO = 0.6 eV, and λ_R = 0.015 eV are adopted to plot c – d/e – f

To explore the valley-contrasting physics in the functionalized Bi systems, a TB model is built for the ML Bi₂XY. We adopt the spherical harmonic functions $\left| {\phi _{\mathrm{ + }}} \right\rangle = - {\textstyle{1 \over {\sqrt 2 }}}\left( {p_x{\mathrm{ + }}ip_y} \right)$and $\left| {\phi _ - } \right\rangle {\mathrm{ = }}{\textstyle{1 \over {\sqrt 2 }}}\left( {p_x - ip_y} \right)$together with the spin {↑,↓} as the basis. The TB Hamiltonian of the ML Bi₂X₂ is first discussed. Under the basis of $\Phi _i{\mathrm{ = }}\{ \left| {\phi _{\mathrm{ + }}} \right\rangle ,\left| {\phi _ - } \right\rangle \} \otimes \{ \uparrow , \downarrow \}$, the Hamiltonian (H₁) can be written in a sum of the nearest-neighbor hopping (H₀) and on-site intrinsic SOC terms (H_SO)³³:

$$H_1 = H_0 + H_{{\mathrm{SO}}}$$

(1)

$$H_0{\mathrm{ = }}\mathop {\sum}\limits_{i \in A} {\mathop {\sum}\limits_{\delta = 1,2,3} {\Phi _i^ + T_\delta \Phi _{i + \delta }} } + H.C.,$$

(2)

$$H_{{\mathrm{SO}}}{\mathrm{ = }}\lambda _{{\mathrm{so}}}\mathop {\sum}\limits_i {\Phi _{\mathrm{i}}^{\mathrm{ + }}\tau _z \otimes \sigma _z\Phi _i} .$$

(3)

In Eqs. (2) and (3), Φ_i represents the annihilation operator on site i. τ_z and σ_z in the equations indicate the Pauli matrices acting on orbital $\left\{ {\left| {\phi _{\mathrm{ + }}} \right\rangle ,\left| {\phi _ - } \right\rangle } \right\}$ and spin {↓,↑} spaces, respectively. δ₁=(1,0), $\delta _2{\mathrm{ = }}( - \frac{1}{2},\frac{{\sqrt 3 }}{2})$, and $\delta _3{\mathrm{ = }}( - \frac{1}{2}, - \frac{{\sqrt 3 }}{2})$ are the three vectors to the nearest-neighbor sites. The T_δ in Eq. (2) takes the forms of

$$\begin{array}{l}T_{\delta _1}{\mathrm{ = }}\left[ {\begin{array}{*{20}{c}} {t_1} & {t_2} \cr {t_2} & {t_1} \end{array}} \right] \otimes \sigma _0,\cr T_{\delta _2}{\mathrm{ = }}\left[ {\begin{array}{*{20}{c}} {t_1} & {z^2t_2} \cr {zt_2} & {t_1} \end{array}} \right] \otimes \sigma _0,\cr T_{\delta _3} = \left[ {\begin{array}{*{20}{c}} {t_1} & {zt_2} \cr {z^2t_2} & {t_1} \end{array}} \right] \otimes \sigma _0,\end{array}$$

(4)

with $z{\mathrm{ = }}\exp (\frac{2}{3}i\pi )$. t₁ and t₂ in Eq. (4) represent the hopping amplitudes. For the ML Bi₂X₂ there are Dirac points existing at the K and K’ points without the SOC, as shown in Fig. 1c. When SOC is considered, nontrivial band gaps of 2λ so are opened at the K and K’ points shown in Fig. 1d, realizing a QSH insulator, in agreement with the ab-initio calculations (see Fig. S1 in Supplementary Information) and previous studies.^30,31,32 The local band gap opened at the Dirac point K (K’) is a result of the first-order relativistic effect related to p_x and p_y orbitals of Bi elements.³¹ Thus, these band gaps are giant and robust (1.160–1.306 eV, see Table S1 in Supplementary Information).

To break the inversion symmetry of the Bi₂X₂ system, we induce a staggered potential (H_U) between the sublattices A and B, equivalently forming the Bi₂XY system. Simultaneously, the Rashba SOC¹² exists in the system due to the different decorations of X and Y. The H_U can be written as $H_U{\mathrm{ = }}U\mathop {\sum}\limits_i {\mu _i\Phi _i^ + } \tau _0 \otimes \sigma _0\Phi _i$, where μ_i = 1 (−1) for the A (B) sublattice and both σ₀ and τ₀ are 2 × 2 unitary matrices. The Rashba SOC H_R can be written as $H_R{\mathrm{ = }}\mathop {\sum}\limits_{i \in A} {\mathop {\sum}\limits_{\delta = 1,2,3} {\Phi _{\mathrm{i}}^{\mathrm{ + }}T_{R\delta }\Phi _{i + \delta }} }$.³³ The resulting TB Hamiltonian for the ML Bi₂XY is thus:

$$H_2{\mathrm{ = }}H_0{\mathrm{ + }}H_{{\mathrm{SO}}}{\mathrm{ + }}H_U + H_R,$$

(5)

where

$$\begin{array}{l}T_{R\delta _1}{\mathrm{ = }} - i\left[ {\begin{array}{*{20}{c}} {\lambda _R} & {\lambda _R^\prime } \cr {\lambda _R^\prime } & {\lambda _R} \end{array}} \right] \otimes \sigma _y,\cr T_{R\delta _2}{\mathrm{ = }}i\left[ {\begin{array}{*{20}{c}} {\lambda _R} & {z^2\lambda _R^\prime } \cr {z\lambda _R^\prime } & {\lambda _R} \end{array}} \right] \otimes (\frac{{\sqrt 3 }}{2}\sigma _x + \frac{1}{2}\sigma _y),\cr T_{R\delta _3}{\mathrm{ = }}i\left[ {\begin{array}{*{20}{c}} {\lambda _R} & {z\lambda _R^\prime } \cr {z^2\lambda _R^\prime } & {\lambda _R} \end{array}} \right] \otimes ( - \frac{{\sqrt 3 }}{2}\sigma _x + \frac{1}{2}\sigma _y),\end{array}$$

(6)

with z = exp(2/3iπ). λ_R, $\lambda _R^\prime$ reflect the Rashba SOC between different orbitals of nearest-neighbor sites. In general, the relation of λ_R and $\lambda _R^\prime$ follows tendency of the t₁ and t₂. We assume $\lambda _R^\prime = \lambda _Rt_2/t_1$ for simplicity and to reduce the number of the independent parameters. The Rashba SOC is important in some systems, which can induce very interesting effects. For example, it opens the topologically nontrivial gap of quantum anomalous Hall effects in graphene system.^34,35 However, in the Bi₂XY system, the Rashba SOC is small compared to intrinsic SOC and staggered potential, which will be shown in the following band fitting. Without the SOC, the bands of the Hamiltonian H₀ + H_U are plotted in Fig. 1e. The spin-up and spin-down bands are degenerate at the K and K’ points. Because of the staggered potential, the Dirac points disappear and two trivial band gaps with the value of 2U emerge at the K and K’ points. With the consideration of the SOC and λ_SO > U, the topologically nontrivial band gaps are opened at the K and K’ points (Fig. 1f). The SOC together with staggered potential lifts the spin degeneracy of energy bands and makes the system have a peculiar spin-valley coupling, as shown in Fig. 1f. An obvious spin splitting appears at both the valence and conduction bands with opposite spin moments in the two valleys. An obvious spin splitting appears at both the valence and conduction bands with opposite spin moments in the two valleys. The calculated Berry curvatures are opposite at different valleys (Fig. 1f), providing an effective magnetic field. Such a magnetic field not only defines the optical selection rules, but also generates an anomalous velocity for the charge carriers. Thus, the valley Hall effect exists in the system. However, in the presence of time-reversal symmetry, the energy bands are still valley degenerate when SOC is considered. The opposite Berry curvatures and spin moments at the two valleys give rise to both the valley and spin Hall effects, without net transverse charge Hall current.

In the real ML Bi (111), the staggered potential can be acquired with different chemical decorations on the upper and lower ML surfaces, namely forming the Bi₂XY (X, Y = H, F, Cl, Br, or I) structure. The calculated staggered potentials are found in the range from 6 meV to 300 meV, as shown in Table S2 and Fig. S2 in Supplementary Information. With the SOC, large nontrivial band gaps from 0.891 to 1.256 eV (see Table S1 and Fig. S3 in Supplementary Information) are opened in the two valleys, giving rise to quantum spin Hall effect and valley Hall effect. These band gaps of the ML Bi₂XY not only give us an opportunity to generate valley polarizations with different wavelength of light,^23,24,25 but also provide a platform for fabricating the wide-frequency valley-light emitting diodes.³⁶ As an example, we now analyze the case of the ML Bi₂HF, where the H atoms bond with the lower Bi atoms and the F atoms bond with the upper Bi atoms. We find that the lattice constant of this ML Bi₂HF is 5.49 Å after a full relaxation. The calculated bond lengths of Bi-H and Bi-F are 1.84 and 2.08 Å, respectively. The energy bands for the ML Bi₂HF without SOC are displayed in Fig. 2a. The band gaps at the K and K’ points are found to be 141 meV. Comparing with Fig. 1c, it can be inferred that the staggered potential 2U in the ML Bi₂HF is about 141 meV, large enough to break the inversion symmetry in the system. When the SOC is turned on, very large nontrivial band gaps of 1.16 eV are opened around the E_F at the K and K’ points. The orbital-resolved band structures for Bi₂HF are shown in Supplementary Fig. S4. It is clear that the bands around the E_F at the two valleys are dominated by the p_x and p_y orbitals of Bi atoms, indicating the constructed TB model can describe the Bi₂HF well. By fitting TB bands to the ab-initio results (shown in Fig. S4), the obtained TB parameters for the ML Bi₂HF are t₁ = 0.73 eV, t₂ = 1.06 eV, 2U = 0.14 eV, λ_SO = 0.61 eV, and λ_R = 0.022 eV. Very obvious spin polarization is also observed in the highest valence bands (HVBs) and the lowest conduction bands (LCBs).

Fig. 2

Band structures and topological properties of the ML Bi₂HF. a and b Band structures for the ML Bi₂HF without and with SOC, respectively. c and d Spin Berry curvatures and Berry curvatures for the whole valence bands of b. The results are obtained based on density-functional theory calculations

To identify the QSH effect and VHE emerging in the ML Bi₂HF, the spin Berry curvature Ω^s(k)¹⁴ and Berry curvature Ω(k)³⁷ are calculated as follows:

$${\mathrm{\Omega }}^s{\mathrm{(}}{\bf{k}}{\mathrm{) = }}\mathop {\sum}\limits_n {f_n} \Omega _n^s({\bf{k}}),$$

(7)

$$\Omega _n^s({\bf{k}}){\mathrm{ = }} - 2{\rm{Im}} \mathop {\sum}\limits_{m \ne n} {\frac{{ < \psi _{n{\bf{k}}}|j_x^s|\psi _{m{\bf{k}}} > < \psi _{m{\bf{k}}}|\upsilon _y|\psi _{n{\bf{k}}} > \hbar }}{{(E_m - E_n)^2}}} ,$$

(8)

$$\Omega {\mathrm{(}}{\bf{k}}{\mathrm{)}} = \mathop {\sum}\limits_n {f_n} \Omega _n({\bf{k}}),$$

(9)

$$\Omega _n({\bf{k}}) = - 2{\rm{Im}} \mathop {\sum}\limits_{m \ne n} {\frac{{ < \psi _{n{\bf{k}}}|\upsilon _x|\psi _{m{\bf{k}}} > < \psi _{m{\bf{k}}}|\upsilon _y|\psi _{n{\bf{k}}} > \hbar ^2}}{{(E_m - E_n)^2}}} .$$

(10)

In Eqs. (7)–(9), E_n is the eigenvalue of the Bloch functions |ψ_nk>, f_n is the Fermi-Dirac distribution function at zero temperature, and $j_{_x}^{\mathrm{s}}$ is the spin current operator defined as (s_zυ_x + υ_xs_z)/2, where υ_x and υ_y are the velocity operators and s_z is the spin operator. The obtained spin Berry curvature Ω^s(k) along the high-symmetry lines is plotted in Fig. 2c. By integrating Ω^s(k) over the first Brillouin zone (BZ), we obtain the spin Chern number Cs = 1, proving that the ML Bi₂HF is a QSH insulator. As shown in Fig. 2d, the calculated Ω(k) is sharply peaked in the valley region, with opposite signs for K and K’, in agreement with Fig. 1f. The distribution of Ω(k) the indicates the valley Hall effect occurring in the system. Namely, when the ML Bi₂XY channel is biased, electrons from different valleys experience opposite Lorentz-like forces and so move in opposite directions perpendicular to the drift current.

To employ the valley degree of freedom, valley splitting ($\Delta _{KK{\prime}}^V$) needs to be introduced, which can be quantified by the energy difference between the topmost valence bands at K ($E_K^V$) and K’ ($E_{K\prime }^V$) valleys, expressed as $\Delta _{KK\prime }^V{\mathrm{ = }}E_K^V - E_{K\prime }^V$.^{16,17,18,19,20,21} In this regard, the principle challenge of using ML Bi₂XY as a valleytronic material is to break the degeneracy between the two prominent K and K’ valleys, protected by time-reversal symmetry. As in TMDs, some strategies of using external fields such as optical pumping,^23,24,25 electric field,⁹ and magnetic field^26,27 are supposed to induce the valley polarizations in the ML Bi₂XY. Importantly, for nonvolatile devices, magnetic doping,^16,17,18 proximity coupling with magnetic substrates^{19,20,21,22,38} or spontaneous valley polarization^15,39 could be desirable to provide intrinsic and robust lifting of the valley degeneracy.^17,21,22 Since the spin and valley degrees of freedom are strongly coupled in the ML Bi₂XY, spin polarization could be exploited to induce valley polarization. Here, we introduce a staggered exchange field $H_M = M_{{\mathrm{A(B)}}}\mathop {\sum }\limits_{i \in A(B)} {\mathrm{\Phi }}_i^ + \tau _0 \otimes \sigma _z{\mathrm{\Phi }}_i$ into the system, where M_A(B) is the local magnetic exchange field in the A (B) sublattice. Such a staggered exchange field has been proven to transform the bands at K and K’ points in the silicence⁴⁰ and functionalized ML Sb,^33,41 leading to so-called quantum spin quantum anomalous Hall (QSQAH) effects.^33,40,41 The staggered exchange field is thus suitable to produce the desired spin-valley polarizations in the ML Bi₂XY. The TB Hamiltonian of the ML Bi₂XY with staggered exchange field can be written as:

$$H_3 = H_0 + H_{{\mathrm{SO}}} + H_U + H_M + H_R$$

(11)

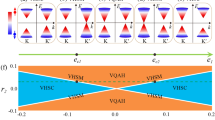
The schematic bands for H₃ without and with SOC are plotted as Fig. 3a, b, respectively. With the staggered exchange field but without SOC, the bands are spin polarized, giving spin splittings of M_A +M_B– 2U and M_A +M_B + 2U for LCBs and HVBs, respectively. When M_A +M_B is larger than 2U, the bands are inverted near the E_F as shown in Fig. 3a. However, the two valleys are still degenerate. Since the SOC of Bi atoms, primarily coming from the p_x and p_y orbitals, is very large, λ_SO > M_A > M_B can be assumed in the TB model calculations. Under this condition, two local band gaps with different values are opened at the K and K’ points, indicating a valley polarization in the system (Fig. 3b). To quantitatively analyze the sequence of the energy levels around the E_F at the K and K’ points, the Rashba SOC is neglected because it is small compared to intrinsic SOC and magnetic field. Analyzing the sequence of the energy levels around the E_F at the two valleys from Fig. 3b (also see Fig. S5 and more details in Supplementary Information), we can obtain the local band gaps at the K and K’ points with the values of 2λ_so– 2M_A and 2λ_so– 2M_B, respectively. These band gaps give rise to an interesting time-reversal-symmetry-broken (TRSB) QSH state.⁴² The calculated spin Berry curvatures (Fig. 3c) and edge states (Fig. 3d) are displayed to identify the interesting TRSB-QSH states. Thus, when the E_F is in the nontrivial band gap ($E_K^C$ > E_F > $E_K^V$), TRSB-QSH edge states could be observed as shown in Fig. 3e.

Fig. 3

Spin-valley polarization and multiple Hall effect in functionalized Bi monolayers. a and b Energy bands for the ML Bi₂XY from the TB model with a staggered exchange field (M_B < M_A< λ_SO) without and with SOC, respectively. The red/blue curves indicate the spin-up/spin-down states. c Spin Berry curvatures and Berry curvatures for the whole valence bands of b. d The band structures of the zigzag nanoribbon (containing 20 zigzag chains in the width) for the system of b. e Schematic of the QSHE. The red/blue arrows indicate the spin-up/down edge states. f Schematic of anomalous charge/spin/valley Hall effects with hole or electron doping. The electrons and holes are indicated by circles with −/+, respectively. The TB parameters of t₁ = 0.8 eV, t₂ = 1.0 eV, 2U = 0.12 eV, M_A = 0.4 eV, and M_B = 0.1 eV, λ_SO = 0.0/0.6 eV, and λ_R = 0.0/0.015 eV are adopted to plot a/b – d

For applications, static and large valley polarization is desirable. In the ML Bi₂XY, the charge carriers in the two valleys have opposite transverse velocities due to the valley degeneracy and opposite signs of the Berry curvatures and thus the total Hall conductivity vanishes because of time-reversal symmetry. With the staggered exchange field induced, the valley splitting is obtained. Considering the energy levels at two valleys (see more details in Supplementary Information) we can get the valley splitting for the valance bands ($\Delta _{KK\prime }^V$) is ΔM + 2U (ΔM = M_A– M_B). Similarly, we can also obtain the valley splitting for the conduction bands ($\Delta _{KK\prime }^C$) of ΔM – 2U. Clearly, the valley splittings in the functionalized ML Bi are determined by the staggered potential (2U) and exchange fields (ΔM). Based on the valley splitting, one can manipulate the charge/spin/valley Hall effect with gate control. For example, when $E_K^V$ > E_F > $E_{K\prime }^V$, the up-spin holes at the K valley produce a transverse current under an in-plane electric field, as shown in Fig. 3f. Remarkably, the transverse current is 100% spin polarized. Thus, the flux of the spin holes carries three observable quantities: charge, spin, and valley-dependent orbital magnetic moments corresponding, respectively, to anomalous charge, spin, and valley Hall effects. Similarly, when $E_{K\prime }^C$ > E_F > $E_K^C$, spin-down electrons will produce a net transverse charge/spin/valley current, as shown in Fig. 3f. Therefore, we create intrinsic and robust valley polarization, instead of the using dynamic methods.^23,24,25 Considering QSHE also exists in the system when$E_K^C$ > E_F > $E_K^V$, multiple Hall effects including TRSB-QSHE, anomalous charge/spin/valley Hall effects can be manipulated by gate voltage control in one single system as shown in Fig. 3e, f. Based on this multiple Hall effects control, we can flexibly manipulate the charge, spin, and valley degrees for transport, which is crucial for spintronics and valleytronics.

In experiments, the staggered exchange fields may be induced by replacing the Y atoms with TM (Cr, Mo, W) atoms, forming Bi₂XTM (X = H, F, Cl, Br, or I; TM = Cr, Mo, or W) structures. To realize this proposal, we calculate the electronic structures of Bi₂HTM (TM = Cr, Mo, or W) MLs by using ab-initio methods. The geometry and calculation details of Bi₂HTM (TM = Cr, Mo, or W) MLs are given in Fig. S6 in Supplementary Information. For convenience, here we give an example results about Bi₂HMo. As shown in Fig. 4a, a distinct exchange field is induced from the Mo atoms, leading to large spin polarization of 369 meV for LCBs and 434 meV for HVBs, respectively. With SOC, local energy gaps of about 210 and 710 meV are opened at the K and K’ points, respectively (Fig. 4b), as well as a significant valley polarization emerges in the system. The orbital-resolved band structures of Bi₂HMo (Fig. S7a) indicate the bands around the E_F at the two valleys are dominated by the p_x and p_y orbitals of Bi atoms. Fitting TB bands to the ab-initio results (shown in Supplementary Fig. S7b), the obtained TB parameters for the ML Bi₂HMo are t₁ = 0.60 eV, t₂ = 0.91 eV, 2U = 0.11 eV, M_A = 0.38 eV, M_B = 0.12 eV, λ_SO = 0.51 eV, and λ_R = 0.017 eV. Since the LCB at Γ point is lower than those at the two valleys, we focus on the discussion of the valley splitting of the HVBs. The valley splitting of HVBs $\Delta _{KK\prime }^V$ in Bi₂HMo is up to 388 meV, which is very large compared to the TMD materials.^21,22 A 3880 Tesla magnetic field is needed if the valley splitting is produced by a magnetic field, since the band shift is typically ∼0.1 meV/T by an external magnetic field^26,27 in experiments. The calculated Berry curvatures (Fig. 4b) indicate the electrons in the valleys indeed experience Lorentz-like forces. The calculation of spin Berry curvatures (Fig. S8a) and edge states (Fig. S8b) indicates Bi₂HMo is in TRSB-QSH states. For the MLs Bi₂HCr and Bi₂HW, the valley splitting of HVBs are 356 and 513 meV (shown in Fig. S9), respectively, both of which are record values and much larger than the previous reported maximum valley splitting.^19,21,22 With these giant valley splittings, we can readily create valley polarization with hole doping in the Bi₂HTM (TM = Cr, Mo, or W) MLs. When E_F is tuned to move down in energy within the range of $\Delta _{KK\prime }^V$(up to 513 meV) shown in Fig. 4b, the spin-up holes at K valley will produce a transversal current under a longitudinal in-plane electric field, giving rise to the anomalous charge/spin/valley Hall effects. Considering doping the TM atoms in the freestanding Bi MLs may be not easy in experiments, we also explore the possibility of depositing TM atoms on the heterostructures of Bi MLs on a SiC substrate (Bi-SiC), which has been fabricated very recently.²⁸ The calculated adsorption energy of Mo atom on the Bi-SiC heterostructure is about 2.0 eV and the bands of Mo@Bi-SiC are similar to those of Mo@BiH (see Supplementary Fig. S10), indicating TM doping can be a realistic way to induce the spin-valley splitting in the Bi MLs.

Fig. 4

Band structures and topological properties of magnetic functionalized Bi monolayers. a and b Band structures for the functionalized Bi MLs with H atoms deposited on the upper surface and Mo atoms deposited on the lower surface (Bi₂HMo) without and with SOC, respectively. c and d Band structures for the Bi₂H/LaFeO₃ heterostructure without and with SOC, respectively. The red and black curves in a and c denote the spin-up and spin-down states, respectively. The blue color in b and d denotes the calculated Berry curvatures for the whole valence bands. The results are obtained based on density-functional theory calculations

Besides doping TM atoms, proximity effects may be more realistic and effective way^43,44 to induce a staggered exchange field in the Bi₂XY system and then give rise to spin-valley polarizations. LaFeO₃ is a G-type antiferromagnetic (AFM) insulator with the Fe sites forming alternating (111) ferromagnetic (FM) planes.⁴⁵ Its (111) surface lattice matches well the Bi₂H₂ lattice with the mismatch of ~1%,^31,46 which has been fabricated with atomic-scale control and has a very high crystallographic quality. Therefore, the LaFeO₃ (111) film is a very promising substrate for the ML Bi₂XY to produce the spin-valley splitting. A heterostructure of the ML Bi₂H on a (111) surface of a LaFeO₃ thin film is designed as displayed in Fig. S6c in Supplementary Information. The calculated large adsorption energy (3.6 eV) for the configuration indicates a very strong interaction between the ML Bi₂H and the substrate. Similar to the effect of doping TM atoms, the substrate also induces a staggered exchange field into the hydrogenated MLs. As shown in Fig. 4c, the Dirac bands of the ML Bi₂H₂ are strikingly spin polarized, located just inside the bulk band gap (2.1 eV) of the LaFeO₃ film. With the SOC considered, local band gaps of about 310 and 420 meV are opened around the K and K’ points (Fig. 4d). The scale of $\Delta _{KK\prime }^V$ is found to be about 78 meV in the heterostructure, which may be tuned further by strain or an electric field. We also calculate the orbital-resolved band structures for the Bi₂H-LaFeO₃ heterostructure as shown in Fig. S7c in Supplementary Information. In this case, the HVBs at the two valleys are still dominated by the p_x and p_y orbitals of Bi atoms but the bands of substrate (LaFeO₃) exist in the nontrivial band gap from p_x and p_y orbitals, making the conduction bands of p_x and p_y orbitals higher than LCBs of the system. Fitting TB bands to the ab-initio results (shown in Supplementary Fig. S7d), the obtained TB parameters for the Bi₂H-LaFeO₃ heterostructure are t₁ = 0.68 eV, t₂ = 1.2 eV, 2U = 0.016 eV, M_A =0.11 eV, M_B =0.03 eV, λ_SO =0.64 eV, and λ_R = 0.012 eV. The calculation of spin Berry curvatures (Supplementary Fig. S8c) and edge states (Supplementary Fig. S8d) shows the Bi₂H-LaFeO₃ heterostructure is a TRSB-QSH insulator. With the hole doping, the anomalous charge/spin/valley Hall effects can also be achieved in the heterostructure.

In summary, we systematically investigated the topological properties and valleytronic behaviors in the functionalized Bi MLs based on TB models and ab-initio calculations. The topologically nontrivial band gaps at the two valleys in the ML Bi₂XY (X, Y = H, F, Cl, Br, or I) are found in the range from 0.891 to 1.256 eV. These band gaps not only give us an opportunity to generate valley polarizations with different wavelength of light, but also provide a platform for fabricating valley-light devices. Spin-valley polarizations can be generated with a staggered exchanged field introduced, which together with the staggered potential is found determining the strength of the valley splitting. The calculated spin Berry curvatures and edge states indicate TRSB-QSHEs could be observed when the E_F is located in the nontrivial gap. The calculated Berry curvatures are nonzero and opposite at different valleys, driving opposite anomalous velocities of Bloch electrons. With electron (hole) doping, the spin-down electrons (spin-up holes) produce a spin-valley polarized net transverse current. Thus, with gate control, multiple Hall effects including QSHEs, anomalous charge, spin and valley Hall effects can be manipulated in the single system. Based on ab-initio calculations, we predict these large spin-valley polarizations and multiple Hall effects can be realized in the Bi₂HTM (TM = Cr, Mo, or W) MLs (with valley splitting of up to maximum 513 meV) or Bi₂H/LaFeO₃ heterostructures (with valley splitting of 78 meV). Our results not only extend the properties of known valleytronic materials, but provide new paths to realize emerging applications in electronics, spintronics, and valleytronics.

Methods

The geometry optimization and electronic structure calculations were performed by using the first-principles method based on density-functional theory (DFT) with the projector-augmented-wave (PAW) formalism,⁴⁷ as implemented in the Vienna ab-initio simulation package (VASP).⁴⁸ All calculations were carried out with a plane-wave cutoff energy of 550 eV and 12 × 12 × 1 Monkhorst-Pack grids were adopted for the first Brillouin zone integral. The Berry curvatures and spin Berry Curvatures for the ML Bi₂HF, Bi₂HMo and the Bi₂H/LaFeO₃ heterostructure are calculated in Wannier function bases.⁴⁹ The geometry structures and more computational details about the ML Bi₂HMo and the Bi₂H/LaFeO₃ heterostructure are given in Supplementary Information.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.