Abstract
Recently we reported an enhanced superconductivity in restacked monolayer TaS2 nanosheets compared with the bulk TaS2, pointing to the exotic physical properties of low dimensional systems. Here we tune the superconducting properties of this system with magnetic field along different directions, where a strong Pauli paramagnetic spin-splitting effect is found in this system. Importantly, an unusual enhancement as high as 3.8 times of the upper critical field Bc2, as compered with the Ginzburg-Landau (GL) model and Tinkham model, is observed under the inclined external magnetic field. Moreover, with the out-of-plane field fixed, we find that the superconducting transition temperature Tc can be enhanced by increasing the in-plane field and forms a dome-shaped phase diagram. An extended GL model considering the special microstructure with wrinkles was proposed to describe the results. The restacked crystal structure without inversion center along with the strong spin–orbit coupling may also play an important role for our observations.
Similar content being viewed by others
Introduction
Superconductivity in low-dimensional systems was investigated extensively recently, due to the fertile physical phenomenon and exotic properties.1,2,3,4 At present, the gate of this research field has just been opened and more interesting phenomena are waiting to be explored. Because of the strong spin–orbit coupling, superconducting transition metal dichalcogenides (TMDs) are investigated intensively in the two-dimensional (2D) limit in recent years.5,6,7,8 A clear enhancement of the in-plane upper critical field was frequently reported in these materials, which was interpreted by the Zeeman-protected Ising superconductivity mechanism. Using a chemical exfoliation method, we have obtained the monolayer TaS2 nanosheets, which were assembled layer-by-layer by vacuum filtration.9,10 Such a restacked material shows superconductivity with Tc (~3.2 K) several times higher than the pristine bulk 2H-TaS2, which supplies a significant platform for studying the intrinsic physical properties of unconventional superconductivity in TMDs. Such an enhancement of Tc is consistent with a previous work by Moratalla et al.,11 although they did not reach the one-layer limit, and finally confirmed by other two groups by mechanically exfoliating TaS2 to monolayer.12,13 The enhancement of Tc was believed to originate from the suppression of the charge-density wave and the increase of the density of states by the process of thickness reduction.9,12 However, an in-depth investigation on the physical behaviors of the restacked TaS2 is lacking and more experiments are required at present. Magnetic field is one of the fundamental tuning parameters to affect the behaviors of a superconductor. In the type-II superconductors, the magnetic field can penetrate into the bulk in the form of quantized vortex lines when it exceeds the lower critical field Bc1.14 In addition, various pair-breaking effect, including the orbital and Zeeman type, can be induced by the magnetic field.
Here we present a detailed investigation on the Abrikosov vortex phase of the above-mentioned superconductor, restacked TaS2 nanosheets, by measuring the conducting properties with magnetic fields along different directions. The in-plane upper critical field \(B_{c2}^{ab}\) is clear larger than the Pauli paramagnetic limiting fields BP, indicating a strong Pauli paramagnetic spin-splitting effects in this material. Importantly, the angle dependence of the upper critical field deviates severely from the Ginzburg-Landau (GL) model and Tinkham model. Moreover, the value of Tc is found to increase with the in-plane field B||ab under a fixed out-of-plane field B||c. Both the intrinsic and extrinsic origins for the observations were discussed and we found that the highly noncentrosymmetric crystal structure, the strong spin–orbit coupling, and the special microstructure with wrinkles are important factors for the unusual behaviors we observed.
Results
Details regarding the samples preparation and resistance measurements are given in the Methods section. By a careful characterization using combining methods, the structure of the restacked TaS2 was determined and reported in our previous paper.9 The inter-layer spacing is close to bulk 2H-TaS2, while the 2H symmetry has been broken after the restacking process because of rotations between different layers (see Figure S1). In such a structure, both the in-plane inversion symmetry in each individual layer and the global inversion symmetry are broken. As a consequent, the inversion symmetry breaking will be severer than the bulk, monolayer, and few layered TaS2 materials. The morphology of the samples were checked by the scanning electron microscope (SEM) and scanning transmission electron microscope (STEM) measurements. Wrinkles can be seen on the flat surface and oxides exist only at the edge of the sample with the width of several nanometers. The content of lithium ions was found to be below the minimum detection limit by the inductively coupled plasma optical emission spectrometer (ICP-OES) measurement. A clear Meissner effect can be seen from the magnetic susceptibility measurements (see Figure S3d). These characterizations can be found in the Supplementary Information.
The resistive transitions of one sample (denoted as #1) measured in magnetic fields for both orientations B||ab and B||c are shown in Fig. 1a, b. Clear different efficiencies for the suppression of superconductivity, revealing the anisotropy of the present material, can be seen by comparing the two figures. To determine the upper critical fields Bc2, a criterion of 90% of the normal state resistivity (ρn) is used and the results are shown in the Fig. 1c for the two orientations. Instead of the square root behavior for the in-plane upper critical field \(\left( {B_{c2}^{ab}\sim \sqrt {1 - T/T_c} } \right)\) expected for the 2D superconductors,5,6,7,8,12 an opposite tendency with a positive curvature is observed. This has been found to be a universal feature of anisotropic three-dimensional (3D) layered superconductors.15,16 This reflects the influence of inter-layer coupling on the in-plane upper critical field of our samples, although such an inter-layer stacking manner does not affect Tc. The value of Bc2 at zero temperature can be estimated using the Werthamer–Helfand–Hohenberg relation17 Bc2 = \(- 0.693 \times \mathrm{d}B_{c2}(T){\mathrm{/}}\left. {\mathrm{d}T} \right|_{T_c} \times T_c\) after the slope \(\mathrm{d}B_{c2}(T){\mathrm{/}}\left. {\mathrm{d}T} \right|_{T_c}\) is obtained from Fig. 1c. In addition, the paramagnetic limiting field BP has a simple relation with Tc, BP = 1.84 × Tc based on the conventional BCS theory.18 The resultant values for the three characteristic fields \(B_{c2}^{ab}\) (in-plane Bc2), \(B_{c2}^c\) (out-of-plane Bc2) and BP are denoted by arrows in Fig. 1c and summarized in Table 1, from which the anisotropy of upper critical field \({\mathrm{\Gamma }} = B_{c2}^{ab}{\mathrm{/}}B_{c2}^c = 11\) is obtained. This value is larger than most of the iron-based superconductors and the copper-based superconductor YBCO.16,19 Moreover, a clear relative relation \(B_{c2}^c < B_P < B_{c2}^{ab}\) can be deduced.
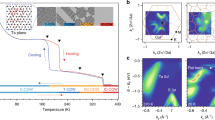
Field-angle resolved experiments were performed by measuring the field (B) and angle (θ) dependence of resistivity at a fixed temperature 2.2 K. As shown in Fig. 2a, one can see how the resistivity is triggered by the field from zero to finite values and saturates gradually at high fields. In order to determine the precise onset superconducting transition point, which reflects the information of upper critical fields Bc2, we show the first derivative dρ/dB of four typical curves in Fig. 2b. As indicated by the arrows, the onset transition point is defined by the characteristic field where the value of dρ/dB begins to increase clearly. The characteristic points determined in Fig. 2b are represented by arrows in Fig. 2a, the connection of which forms a slightly inclined straight line as shown by the blue dashed line. Based on this line reflecting the normal states resistance ρn, a criterion of 90%ρn, as revealed by the black dashed line, is adopted to define the upper critical fields. The crossing points between this black dashed line and the data curves in Fig. 2a determine the upper critical field at different angles Bc2(θ). Angle dependence of Bc2(θ) normalized by \(B_{c2}^c\) is shown in Fig. 2c. One can see the detailed evolution of \(B_{c2}(\theta ){\mathrm{/}}B_{c2}^c\) versus θ. In order to quantitatively evaluate such an angle dependent variation, we employ two theoretical models, the 3D GL model and 2D Tinkham model20,21 (see SI), and plot the curves based on them for comparison. These two models show slight differences near θ = 0°, which is usually used to distinguish the 2D superconductivity in monolayer or interfacial systems.6,7,22 However, the difference between our experimental data and the two models is much larger, showing a great enhancement of upper critical field in a wide angle range. In the strong anisotropic system, the perpendicular component of the the upper critical field Bc2(θ)sinθ is expected to be dominant in the low angle range since the in-plane magnetic field is not important in terms of suppressing Tc. So we show this component normalized by \(B_{c2}^c\) in Fig. 2d, where a broad peak-shaped experimental curve with the maximum enhancement of 3.8 times is observed.
The measurements of the upper critical field along different directions Bc2(θ) for sample #1. a Field dependence of resistivity with the external field rotating from B||ab (θ = 0°) to B||c (θ = 90°) at a fixed temperature T = 2.2 K. b Differential of the ρ–B curves in a, based on which the onset superconducting transition points are determined and indicated by the black arrows. c Angle dependence of the upper critical field Bc2(θ) normalized by \(B_{c2}^c\). d Angle dependence of perpendicular component of the upper critical field Bc2(θ)sinθ normalized by \(B_{c2}^c\). In c,d, the theoretical curves based on the GL model and Tinkham model are shown in comparison with the experimental data
Actually such an upper-critical-field-enhancement effect can induce very fascinating features in Tc in the mixed state. Here we adopt a different mode of measurements: ρ–T curves are measured with the out-of-plane field B||c fixed and the in-plane field B||ab increasing, as schematized in the inset of Fig. 3b. The current is applied in the direction perpendicular to B||ab. This method has been used to identify the 2D or interfacial superconductivity, where the curves will overlap with each other because B||ab is not important in an extremely 2D superconductor.22,23 While in an anisotropic system with 3D features, Tc will be reasonably suppressed by B||ab (see section 7 of SI). In Fig. 3a we show a typical set of data with B||c = 0.4 T on another sample denoted as #2 with a similar Tc as #1. The behavior is uniquely different from the above-mentioned two categories. The superconducting transition is enhanced clearly following by a suppression with the increase of B||ab. Three criterions, 10, 50, and 90%ρn, are employed to determine the critical transition temperature Tc and the results are shown in Fig. 3b. All the three curves show the dome-like features, confirming that it is an intrinsic property rather than a magnetic flux-related behavior. The dome-like behavior may reveal the presence of competing between some unconventional effect and the pairing-breaking effect induced by magnetic field. Figure 3c summarizes the effect of B||ab on Tc at different B||c, where Tc is determined using the criterion 50%ρn. The maximum Tc for the three curves emerges at the same ratio B||ab/B||c, indicating a characteristic angle θ ~20°, along which the detrimental effect of magnetic field is mostly suppressed.
Electrical resistivity data and the critical transition temperature in the inclined field with B||c fixed and B||ab increasing for sample #2. a ρ–T curves with B||c = 0.4 T and B||ab increasing. b B||ab dependence of Tc determined from the data in a by three criterions 10, 50, and 90%ρn. The inset shows a sketch map of the field configuration for the measurements. B||ab is applied perpendicular to the current. c B||ab (normalized by B||c) dependence of the Tc enhancement by the criterion 50%ρn under three fixed B||c = 0.2, 0.4, and 0.8 T
Discussion
The detailed investigations on the thickness dependence of superconducting behaviors of 2H-TaS212 supply a good coordinate to make a comparison with our results. It is found that the critical transition temperature Tc increases with the decrease of thickness and reaches 3.4 K for monolayer TaS2. This value is very close to our sample, confirming the monolayer-features of our sample and suggesting that the restacking process imposed on the monolayer TaS2 does not affect Tc of this system. Moreover, the normal state resistivity displays a T2.45 behavior in low temperature in our sample (see Figure S4), corresponding to the situation between 3-layer (~T2) and 7-layer (~T3) for the ordered stacked TaS2.12 This implies that the inter-layer coupling in our samples shows a certain degree of influence on the electrical transport behavior. A more careful examination shows that the out-of-plane upper critical field \(B_{c2}^c\) is similar to the bilayer TaS2, while the in-plane \(B_{c2}^{ab}\) and the anisotropy are only one third of the bilayer TaS2. Nevertheless, \(B_{c2}^{ab}\) of our samples is clearly larger than that of the bulk samples since the latter does not exceed the Pauli limit. All in all, the present samples are different from both the monolayered and the bulk TaS2. The restacked TaS2 monolayers maintain the enhanced Tc (compared with the bulk material), while lose the 2D characters and show an anisotropic 3D features. This is the basis of the following discussions.
Field-induced superconductivity has been theoretically proposed for ferromagnetic materials and is known as Jaccarino-Peter compensation effect.24 In this effect, the internal magnetic field created by the magnetic moments through the exchange interaction can be compensated by the external magnetic field and superconductivity will occur. This mechanism has been realized in Eu–Sn molybdenum chalcogenides experimentally.25 Moreover, another theory proposed by Kharitonov and Feigelman considered the polarization of magnetic impurity spins induced by the in-plane field and predicted an enhancement of superconductivity, especially in disordered films.26 Evaluating the performances of our samples, we found that neither of the two theories is applicable. First of all, our magnetization measurement shows a paramagnetic behavior in our samples (see Figure S3c), which excludes the presence of long-range magnetic moments and magnetic impurities. Secondly, the enhancement of Tc by in-plane field in our samples can only be observed in the presence of out-of-plane field, which is rather different from the case of the above-mentioned scenarios.
Intuitively, the theoretical proposal27,28,29 predicting a field-induced triplet component in the order parameter of the singlet superconductors due to the Pauli paramagnetic spin-splitting effect is very consistent with our observation shown in Fig. 2d. According to their arguments, such an enhancement of Bc2(θ) should be conspicuous in anisotropic superconductors with \(B_{c2}^c \ll B_P \ll B_{c2}^{ab}\). However, we note that such an exotic behavior is absent in so many low-dimensional TMDs with even stronger Pauli paramagnetic spin-splitting effect,6,7 which weakens the persuasion of this interpretation. Other important factors should be considered to interpret our experiments. One important clue for exploring the physical origination is that such a rare behavior was also observed in restacked 1T′-MoS2 (see Figure S7) prepared with the similar process30 to that used in restacked TaS2. This implies that the unique and common features of such restacked monolayered materials are key factors for our observations. One most conspicuous feature for such restacked monolayer materials is the noncentrosymmetric crystal structure as mentioned in the beginning of the Results section. It has been discussed a lot both theoretically and experimentally that the noncentrosymmetric crystal structure along with strong spin-orbit coupling (SOC), which also exists in the present compound with 5d metal, is very favorable to incur the spin-triplet component in the superconducting order parameter.31,32,33,34,35,36,37 This may be one possible origin of our observations. One positive evidence for this scenario is that the restacked 1T′-MoS2, which have a weaker SOC because of the lighter 4d Mo element, shows an inconspicuous enhancement of Bc2(θ) compared with restacked TaS2 (see Figure S7).
One possible extrinsic origination to explain our results comes from the possible orientation mismatch or wrinkles (see Figure S2) of the monolayer TaS2 sheets during the restacking process, which affects the c-axis orientation of the restacked samples. In section 9 of SI, we carefully analyzed the influences of different orientations on the estimation of Bc2 and found that Bc2 is mainly determined by the high-Tc portion where the included angle between the surface and field is the smallest. The presence of the low-Tc portion with a larger included angle can lower the onset transition temperature slightly (see Figure S8). The simple GL model20 is not applicable any more in this case. Considering the misaligned angle Δθ resulting from the wrinkles as schematically displayed in the inset of Fig. 4(a), we proposed an extended GL (EGL) model:
where Θ = min|θ − Δθ| is the smallest included angle between the surface and field, and A(θ) is an adjusting parameter taking into account the effect of the low-Tc portion with other orientations. Here we simply assume that A(θ) is proportional to the GL formula, because A(θ) will be larger when Tc is more sensitive with the orientation, which can be reflected by the GL formula. Typically the misaligned angle Δθ has a distribution range with a maximum ΔθMax. Then we have
a The comparison between the angle dependence of upper critical field and the extended GL (EGL) model considering the influence of the wrinkles. b The comparison between the angle dependence of experimental upper critical field and the practical field applied in the experiments shown in Fig. 3. c The comparison between the GL model and the practical field applied in the experiments shown in Fig. 3
By tuning the value of parameters, it is found that when ΔθMax = 27°, this EGL model can well describe the experimental data in the range θ > ΔθMax, as shown in Fig. 4a. As for the case of θ ≤ ΔθMax, Bc2(θ) is only determined by the adjusting parameter A(θ). However, the influence factors on A(θ) are rather complicated in this region, so we could not get a good description at present. At this stage, we could not exclude the possibility that the wrinkles have an important influence on our observations. Even in this scenario, our results supplied an interesting prototypical system showing an unambiguous relationship between the microstructure and the physical (superconducting) performance. Moreover, this is also valuable in designing devices for applications.
It is notable that the enhancement of Tc by B||ab at the presence of B||c is simply a natural consequence of the unusual behavior in Bc2(θ). As shown in Fig. 4b, c, supposing a linear suppression of Bc2 with the temperature approaching Tc: Bc2(T) ~1 − T/Tc, angle dependence of Bc2(θ) at other temperatures can be derived from the data at 2.2 K for both the experimental data and GL model, respectively. The total values of field in the experiment of Fig. 3, \(\sqrt {B_{||ab}^2 + B_{||c}^2}\), are also plotted for comparison. The intersections between the two sets of curves indicate the values of Tc. With the decrease of θ, the intersection in Fig. 4b moves to high temperatures until the orientation around 20–30°, and then moves to low temperatures for both cases with B||c = 0.2 T and B||c = 0.4 T. This reproduces the variation of Tc with angle as shown in Fig. 3b, c. In the normal situation as shown in Fig. 4c, the value of \(\sqrt {B_{||ab}^2 + B_{||c}^2}\) evolves along the tracing of GL model at a certain temperature in a rather wide angle range and moves to low temperature slightly in low angle region.
To summarize, we have measured angle-resolved electrical resistivity of the restacked TaS2 nanosheets under magnetic field along different directions. It is found that Pauli paramagnetic limit is broken through in the mixed state, placing the present superconducting system in the environment suffering a strong Pauli paramagnetic spin-splitting effect. A clear enhancement of the upper critical field, as compared with the GL model and Tinkham model, is observed in inclined magnetic field. The critical transition temperature can be enhanced by the in-plane field at the presence of the out-of-plane field. Our analysis indicates that the highly noncentrosymmetric crystal structure, the strong spin–orbit coupling and the special microstructure with wrinkles are important factors for the mechanism of the unusual behaviors we observed.
Methods
Sample preparation
The restacked TaS2 nanosheets were obtained by a chemical exfoliation method followed by the vacuum filtration.9,10 Firstly 2H-TaS2 powders were prepared by the solid-state reaction. Then the LixTaS2 powders were synthesized by soaking as-prepared 2H-TaS2 powders in n-butyl lithium solution. The as-prepared LixTaS2 crystals were exfoliated in distilled water. The redox reaction occurs at this stage. The obtained colloidal solution is composed of TaS2 monolayers and is rather stable. The restacked TaS2 nanosheets were obtained from the vacuum filtration of the colloidal suspension. The restacked TaS2 samples are stable in air within 24 h (see Figure S2).
Morphology characterization
The morphology of restacked TaS2 nanosheets was characterized by JSM-6510 SEM. The atomic structures were observed through JEOL ARM-200F High-angle annular dark field (HAADF) STEM.
Resistance measurements
The restacked samples for the electrical transport measurements have the thickness of about 1 μm. The electrical transport data were collected by the standard four-probe method with magnetic field rotating in the plane perpendicular to the electric current. θ denoted the included angle between external field B and the ab-plane of the crystal. The applied electric current is 10 μA when carrying out the resistivity measurements and up to 50 mA for the I–V measurements.
Data availability
All relevant data are available from the corresponding author.
References
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Gozar, A. et al. High-temperature interface superconductivity between metallic and insulating copper oxides. Nature 455, 782–785 (2008).
Wang, Q.-Y. et al. Interface-induced high-temperature superconductivity in single unit-cell fese films on SrTiO3. Chin. Phys. Lett. 29, 037402 (2012).
Saito, Y., Nojima, T. & Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mat. 2, 16094 (2016).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Saito, Y. et al. Superconductivity protected by spin-valley locking in ion-gated MoS2. Nat. Phys. 12, 144–149 (2016).
Lu, J. M. et al. Evidence for two-dimensional ising superconductivity in gated MoS2. Science 350, 1353–1357 (2015).
Xing, Y. et al. Ising superconductivity and quantum phase transition in macro-size monolayer NbSe2. Nano. Lett. 17, 6802–6807 (2017).
Pan, J. et al. Enhanced superconductivity in restacked TaS2 nanosheets. J. Am. Chem. Soc. 139, 4623–4626 (2017).
Guo, C. et al. High-quality single-layer nanosheets of MS2 (M = Mo, Nb, Ta, Ti) directly exfoliated from AMS2 (A = Li, Na, K) crystals. J. Mater. Chem. C 5, 5977–5983 (2017).
Moratalla, E. N. et al. Enhanced superconductivity in atomically thin TaS2. Nat. Commun. 7, 11043 (2016).
Yang, Y. et al. Enhanced superconductivity and suppression of charge-density wave order in 2H-TaS2 in the two-dimensional limit. arXiv: 1711.00079 (2017).
de la Barrera, S. C. et al. Tuning ising superconductivity with layer and spin-orbit coupling in two-dimensional transition-metal dichalcogenides. Nat. Commun. 9, 1427 (2018).
Abrikosov, A. A. Fundamentals of Theory of Metals (Elsevier, New York, NY 1988).
Woollam, J. A. & Somoano, R. B. Superconducting critical fields of alkali and alkaline-earth intercalates of MoS2. Phys. Rev. B 13, 3843–3853 (1976).
Ma, Y. et al. Strong anisotropy effect in an iron-based superconductor CaFe0.882Co0.118AsF. Supercond. Sci. Technol. 30, 074003 (2017).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, H c2. III. electron spin and spin-orbit effects. Phys. Rev. 147, 295–302 (1966).
Clogston, A. M. Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 9, 266–267 (1962).
Yuan, F. F. et al. Anisotropy of iron-platinum-arsenide Ca10(PtnAs8)(Fe2−xPtxAs2)5 single crystals. Appl. Phys. Lett. 107, 012602 (2015).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1388 (1994).
Harper, F. E. & Tinkham, M. The mixed state in superconducting thin films. Phys. Rev. 172, 441–450 (1968).
Zhou, W. et al. Anomalous electron doping independent two-dimensional superconductivity. New J. Phys. 19, 073014 (2017).
Wu, J. et al. Anomalous independence of interface superconductivity from carrier density. Nat. Mater. 12, 877–881 (2013).
Jaccarino, V. & Peter, M. Ultra-high-field superconductivity. Phys. Rev. Lett. 9, 290–292 (1962).
Meul, H. W. et al. Observation of magnetic-field-induced superconductivity. Phys. Rev. Lett. 53, 497–500 (1984).
Kharitonov, M. Y. & Feigelman, M. V. Enhancement of superconductivity in disordered films by parallel magnetic field. JETP Lett. 82, 421–425 (2005).
Lebed, A. G. Cooper pairs with broken parity and spin-rotational symmetries in d-wave superconductors. Phys. Rev. Lett. 96, 037002 (2006).
Lebed, A. G. Type-IV superconductivity: can superconductivity be more exotic than unconventional? J. Low. Temp. Phys. 142, 173–178 (2006).
Dutta, O. & Lebed, A. G. Cooper pairs with broken time-reversal, parity, and spin-rotational symmetries in singlet type-II superconductors. Phys. Rev. B 78, 224504 (2008).
Guo, C. et al. Observation of superconductivity in 1T’-MoS2 nanosheets. J. Mater. Chem. C. 5, 10855–10860 (2017).
Gor’kov, L. P. & Rashba, E. I. Superconducting 2D system with lifted spin degeneracy: mixed singlet-triplet state. Phys. Rev. Lett. 87, 037004 (2001).
Frigeri, P. A., Agterberg, D. F., Koga, A. & Sigrist, M. Superconductivity without inversion symmetry: MnSi versus CePt3Si. Phys. Rev. Lett. 92, 097001 (2004).
Samokhin, K. V. Paramagnetic properties of noncentrosymmetric superconductors: application to CePt3Si. Phys. Rev. Lett. 94, 027004 (2005).
Frigeri, P. A., Agterberg, D. F. & Sigrist, M. Spin susceptibility in superconductors without inversion symmetry. New J. Phys. 6, 115 (2004).
Yuan, H. Q. et al. S-wave spin-triplet order in superconductors without inversion symmetry: Li2Pd3B and Li2Pt3B. Phys. Rev. Lett. 97, 017006 (2006).
Nishiyama, M., Inada, Y. & Zheng, G.-q Spin triplet superconducting state due to broken inversion symmetry in Li2Pt3B. Phys. Rev. Lett. 98, 047002 (2007).
Yogi, M. et al. Evidence for novel pairing state in noncentrosymmetric superconductor CePt3Si: 29Si-NMR knight shift study. J. Phys. Soc. Jpn. 75, 013709 (2006).
Acknowledgements
This work is supported by the Youth Innovation Promotion Association of the Chinese Academy of Sciences (No. 2015187), the National Natural Science Foundation of China (No. 11204338), and the “Strategic Priority Research Program (B)” of the Chinese Academy of Sciences (No. XDB04040300).
Author information
Authors and Affiliations
Contributions
G.M. and F.Q.H. designed the experiments. Y.H.M. performed the measurements. J.P. and C.G.G. synthesized the samples. G.M. analysed the data. Y.H.M., J.P., C.G.G., X.Z., L.L.W., T.H., G.M., F.Q.H., and X.M.X. discussed the results. G.M. and F.Q.H. wrote the paper. X.M.X. supervised the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ma, Y., Pan, J., Guo, C. et al. Unusual evolution of Bc2 and Tc with inclined fields in restacked TaS2 nanosheets. npj Quant Mater 3, 34 (2018). https://doi.org/10.1038/s41535-018-0107-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0107-2