Introduction

Assessing the properties of interacting fermionic systems constitutes one of the core tasks of modern physics, a task that has a wealth of applications in quantum chemistry1, condensed matter physics2, and materials science3. Notions of quantum simulation offer an alternative route to studying this important class of systems. In analog simulation, one prepares the system of interest under highly controlled conditions. However, any such effort makes sense only if one has sufficiently powerful readout techniques available that allow one to estimate properties. In fact, the read-out step constitutes a core bottleneck in many schemes for quantum simulation.

Fortunately, for natural fermionic systems, one often does not need to learn the full unknown quantum state; trying to do so regardless would be highly impractical, as the resources required for a full tomographic recovery would scale exponentially with the size of the system. Instead, what is commonly needed are the so-called k-particle reduced density matrices, abbreviated as k-RDMs. These are expectation values of polynomials of fermionic operators of the 2k-th degree. Naturally, the expectation value of any interaction fermionic Hamiltonian can be estimated using 2-RDMs only4,5. Indeed, the adaptive variational quantum algorithm (VQE)6 also utilizes up to 4-RDMs to simulate many-body interactions in the ground and excited state7,8. That is to say, meaningful methods of read-out often focus on estimating such fermionic reduced density matrices.

On the highest level, several approaches can be pursued when dealing with fermionic operators. One of those—and the one followed here—is to treat the fermionic system basically as a collection of spins. Then given spin Hamiltonians \({\left\{{H}_{i}\right\}}_{i = 1}^{m}\) and an unknown quantum state ρ, where \(m={{{\mathcal{O}}}}\left({{{\rm{poly}}}}(n)\right)\), the classical shadow (CS) algorithm or its variants9,10,11,12,13,14,15,16,17,18,19,20,21 in qubit systems are among the most promising ways to calculate the expectations \({{{\rm{Tr}}}}\left(\rho {H}_{i}\right)\), with the representation of the Hamiltonians \({\left\{{H}_{i}\right\}}_{i = 1}^{m}\) in the Pauli basis, which invokes a fermion-to-spin mapping such as the Jordan-Wigner22,23 or Bravyi-Kitaev encodings24,25. We define the classical shadow channel as \({{{\mathcal{M}}}}\), which involves operating the unitary channel \({{{\mathcal{U}}}}\) uniformly randomly sampled from the Clifford group before measurements in the Z-basis and classical postprocessing operations on the measurement outcomes. By performing the inverse of the classical shadow channel \({{{{\mathcal{M}}}}}^{-1}\) on the resulting state after performing \({{{\mathcal{M}}}}\) on the initial state ρ, we obtain the classical shadow representation \(\hat{\rho }\) of the quantum state ρ, allowing for the calculation of the expected values of observables \({\left\{{H}_{i}\right\}}_{i = 1}^{m}\) with respect to ρ using classical methods.

While the classical shadow algorithm requires exponentially many copies even for some local interacting fermions due to the inefficient representation in the qubit system, recently, several classical shadow algorithms for fermionic systems without encoding of the Hamiltonians have been proposed26,27,28. Zhao, Rubin, and Miyake26 utilize the generalized CS method9 for fermionic systems, and proposed an algorithm that requires \({{{\mathcal{O}}}}((\begin{array}{l}n\\ k\end{array}){k}^{3/2}(\log n)/{\varepsilon }^{2})\) copies for the unknown quantum states to output all the elements of a k-RDM. Low27 proves that all elements of the k-RDM can be estimated with \(\left(\begin{array}{l}\eta \\ k\end{array}\right){(1-\frac{\eta -k}{n})}^{k}\frac{1+n}{1+n-k}/{\varepsilon }^{2}\) number of copies of the quantum state, where η is the number of particles and n is the number of modes. These fermionic shadow estimation methods (along with the generic classical shadow formalism) do not account for noise in the system, which is an inevitability in real physical systems.

Since we are still in the noisy intermediate-scale quantum (NISQ) era, current quantum simulators are heavily affected by noise; hence, any characterization technique needs to be robust for these simulators to be useful. For qubit systems, robust shadow estimation was developed29,30 where Chen et al.29 use techniques from randomized benchmarking to mitigate the effect of gate-independent time-stationary Markovian (GTM) noise channels on the procedure. Jnane et al.31 proposed error-mitigated classical shadow with probabilistic error cancellation.

Utilizing the robust shadow estimation scheme and taking inspiration from the fermionic shadow estimation of Zhao et al.26,28, we present an error-mitigated shadow estimation scheme for fermionic systems and demonstrate its feasibility for realistic noise channels. Note that akin to the fermionic CS approaches proposed in refs. 26,28, our error-mitigated CS method circumvents the need to encode the Hamiltonian using the qubit representation.

We sample our unitaries \({{{{\mathcal{U}}}}}_{Q}\) from the matchgate group32, a natural choice for our protocol as there is a one-to-one correspondence between two-qubit matchgates and free-fermionic evolution33,34. We therefore design the classical postprocessing operations by leveraging the irreducible representation of the matchgate group. We successfully introduce an unbiased estimator \(\widehat{{{{\mathcal{M}}}}}\) for the noisy classical shadow channel \(\widetilde{{{{\mathcal{M}}}}}\), where we require an additional calibration protocol to generate the estimator \(\widehat{{{{\mathcal{M}}}}}\) with the assumption that the computational basis state \(\left\vert {{{\boldsymbol{0}}}}\right\rangle \,\left\langle {{{\boldsymbol{0}}}}\right\vert\) can be prepared noiselessly. Additionally, we demonstrate the efficacy of our protocol under conditions of constant noise strength by evaluating its performance across various common noise channels: depolarizing noise, generalized amplitude damping, X-rotation, and Gaussian unitary noise. The number of samples required for the estimation process of our protocol is in the same order as the noise-free matchgate classical shadow scheme26,28.

We determine the effectiveness of our protocol with the above noise models by calculating the expectations of all elements of the k-particle reduced density matrix (k-RDM) when the noise strength is constant. The number of samples required for estimation, in this case, is \({{{\mathcal{O}}}}\left(k{n}^{k}\ln (n/{\delta }_{e})/{\varepsilon }_{e}^{2}\right)\) and for calibration is \({{{\mathcal{O}}}}\left(\sqrt{n}\ln n\ln (1/{\delta }_{c})/{\varepsilon }_{c}^{2}\right)\) with error εe + εc and success probability (1 − δe)(1 − δc).

We have extended the analysis of our error-mitigated fermionic shadow channel estimation to more general physical quantities inspired by the fermionic shadow analysis of Wan et al.28, with more details in Supplementary Notes 5, 9. We list distinct classical shadow approaches in both noiseless and noisy qubit and fermionic systems in Table 1. Our error-mitigated fermionic classical shadow technique constitutes an extension of the work by Chen et al.29, accommodating scenarios where the gate-set lacks (1) 3-design properties35 and (2) the applicability of the randomized benchmarking scheme developed by Helsen et al.36.

Table 1 Enumeration of the classical shadow protocols in noiseless and noisy settings, for qubit and fermionic systems respectively
Full size table

We tested the accuracy and efficacy of our protocol by performing numerical experiments to estimate \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\) (where \({\widetilde{\gamma }}_{S}={U}_{Q}^{{\dagger} }{\gamma }_{S}{U}_{Q}\), where γS is the product of \(\left\vert S\right\vert\) Majorana operators and plays a crucial role in computing k-RDMs) on a noisy quantum device subjected to various types of gate noise such as depolarizing, generalized amplitude damping, X-rotation, and Gaussian unitaries. Our numerical investigations confirm the potential of our methods in real-world experimental scenarios.

Results

Basic notations and concepts

Here we give the basic notations and concepts that will be used throughout this work.

Basic notations

The symbols X, Y, and Z denote the Pauli X, Y, and Z operators respectively. The operator \({R}_{X}(\theta )=\exp \left(-i\frac{\theta }{2}X\right)\) denotes the rotation operator around the x-axis. A Z-basis measurement is performed with respect to the basis of eigenstates of the Pauli-Z operator. We utilize \({\mathbb{I}}\) to represent the identity operator on the full system. The set of linear operators on a vector space \({{{\mathcal{H}}}}\) is denoted as \({{{\mathcal{L}}}}({{{\mathcal{H}}}})\). We utilize the symbol \(\widetilde{{{{\mathcal{O}}}}}\) to omit the logarithmic terms.

Superoperator

We denote the superoperator representation of a linear operator \(O\in {{{\mathcal{L}}}}({{{\mathcal{H}}}})\) as \(\left.\left\vert O\right\rangle \!\right\rangle := O/\sqrt{{{{\rm{Tr}}}}\left(O{O}^{{\dagger} }\right)}\) and the scaled Hilbert-Schmidt inner product between linear operators as \(\left\langle \!\langle O| R\rangle \!\right\rangle ={{{\rm{Tr}}}}\left({O}^{{\dagger} }R\right)/\sqrt{{{{\rm{Tr}}}}\left(O{O}^{{\dagger} }\right){{{\rm{Tr}}}}\left(R{R}^{{\dagger} }\right)}\). The action of a channel \({{{\mathcal{E}}}}\in {{{\mathcal{L}}}}({{{\mathcal{L}}}}({{{\mathcal{H}}}}))\) operating on a linear operator \(O\in {{{\mathcal{L}}}}({{{\mathcal{H}}}})\) can hence be written as \({{{\mathcal{E}}}}\left.\left\vert O\right\rangle \,\right\rangle ={{{\mathcal{E}}}}(O)/\sqrt{{{{\rm{Tr}}}}\left(O{O}^{{\dagger} }\right)}\). The channel representation of a measurement with respect to the computational basis can be represented as \({{{\mathcal{X}}}}={\sum }_{x\in {\left\{0,1\right\}}^{n}}\left.\left\vert x\right\rangle \!\right\rangle \,\left\langle \!\left\langle x\right\vert \right.\). We denote the unitary channel corresponding to the unitary operator U as \({{{\mathcal{U}}}}(\cdot )=U(\cdot ){U}^{{\dagger} }\).

Majorana operator

The Majorana operators γj for 1≤j≤2n describes the fermionic system with \({\gamma }_{j}={b}_{(j+1)/2}+{b}_{(j+1)/2}^{{\dagger} }\) for odd j and \({\gamma }_{j}=-i({b}_{j/2}-{b}_{j/2}^{{\dagger} })\) for even j, where bj and \({b}_{j}^{{\dagger} }\) are the annihilation and creation operators, respectively, associated with the j-th mode. Let γS be the product of the Majorana operators indexed by the subset S, denoted as \({\gamma }_{S}={\gamma }_{{l}_{1}}\cdots {\gamma }_{{l}_{| S| }}\) for \(\left\vert S\right\vert > 0\) and \({\gamma }_{{{\emptyset}}}={\mathbb{I}}\), where \(S=\left\{{l}_{1},\ldots ,{l}_{| S| }\right\}\) and l1 < l2 < … < l∣S∣. It can be shown that γS forms the complete orthogonal basis for \({{{\mathcal{L}}}}({{{\mathcal{H}}}})\) for S ⊆ [2n]. Let \({{{\Gamma }}}_{k}:= \left\{{\gamma }_{S}| \left\vert S\right\vert =k\right\}\) be the subspace of γS with cardinality k. We denote the even subspace as \({{{\Gamma }}{}_{{{{\rm{even}}}}}:= \bigoplus }_{l}{{{\Gamma }}}_{2l}\). Also, we denote \({{{{\mathcal{P}}}}}_{k}\) as the projector onto the subspace Γk, i.e.

$${{{{\mathcal{P}}}}}_{k}=\mathop{\sum}\limits_{S\in \tiny{\left(\begin{array}{l}[2n]\atop k\end{array}\right)}}\left.\left\vert {\gamma }_{S}\right\rangle \!\right\rangle \left\langle \!\left\langle {\gamma }_{S}\right\vert \right.,$$
(1)

where we have used the notation that for a set A and an integer k, \((\begin{array}{l}A\\ k\end{array})=\{T\subseteq A:| T| =k\}\) denotes the set of subsets of A with cardinality k.

Gaussian unitaries

Matchgates are in a one-to-one correspondence with the fermionic Gaussian unitaries and can serve as a qubit representation for these unitaries. We denote \({{\mathbb{M}}}_{n}\) as the matchgate group, and write its elements \({U}_{Q}\in {{\mathbb{M}}}_{n}\) in terms of rotation matrices Q belonging to the orthogonal group Orth(2n) (see Supplementary Note 1 for details)33,37. Following Wan et al.’s study28, which demonstrated that the continuous matchgate group \({{\mathbb{M}}}_{n}\) and the discrete subgroup \({{\mathbb{M}}}_{n}\cap {{{{\rm{Cl}}}}}_{n}\) (where Cln represents the Clifford group) deliver equivalent performances for fermionic classical shadows, our findings remain applicable to both continuous and discrete matchgate circuits. Since \({U}_{Q}^{{\dagger} }{\gamma }_{j}{U}_{Q}={\sum }_{k}{Q}_{jk}{\gamma }_{k}\), the matchgate UQ transforms the product of Majorana operators γS in the Γ∣S∣ subspace as \({U}_{Q}^{{\dagger} }{\gamma }_{S}{U}_{Q}={\sum }_{{S}^{{\prime} }\in {\tiny\left(\begin{array}{l}[2n]\atop | S| \end{array}\right)}}\det (Q{| }_{S{S}^{{\prime} }}){\gamma }_{{S}^{{\prime} }}\).

k-particle reduced density matrices (k-RDM)

We denote a k-RDM as kD, which can be obtained by tracing out all but k particles. Here we denote it as a tensor with 2k indices,

$${}^{{{{\boldsymbol{k}}}}}{{{{\bf{D}}}}}_{{j}_{1},\ldots ,{j}_{k};{l}_{1},\ldots ,{l}_{k}}={{{\rm{Tr}}}}\left(\rho {b}_{{j}_{1}}^{{\dagger} }\cdots {b}_{{j}_{k}}^{{\dagger} }{b}_{{l}_{1}}\cdots {b}_{{l}_{k}}\right),$$
(2)

where ji and li are in [n] for i ∈ [k]. The fermionic system can be equivalently described in the Majorana basis, in which case a tensor can be rewritten as the linear combinations of \({{{\rm{Tr}}}}\left(\rho {\gamma }_{S}\right)\), and \(\left\vert S\right\vert \le 2k\). Hence all n2k elements of the k-RDM can be obtained by calculating \({{{\rm{Tr}}}}\left(\rho {\gamma }_{S}\right)\), for the scaling of \({{{\mathcal{O}}}}\left({n}^{k}\right)\) different S with \(\left\vert S\right\vert \le 2k\)38.

Pfaffian function

The Pfaffian of a matrix \(Q\in {{\mathbb{R}}}^{2n\times 2n}\) is defined as

$${{{\rm{pf}}}}(Q)=\frac{{2}^{n}}{n!}\mathop{\sum}\limits_{\sigma \in {S}_{2n}}{{{\rm{sgn}}}}\left(\sigma \right)\mathop{\prod }\limits_{i=1}^{n}{Q}_{{\sigma }_{2i-1},{\sigma }_{2i}},$$
(3)

which can be calculated in \(O\left({n}^{3}\right)\) time39.

Ideal fermionic shadow (Wan et al.28)

Given an unknown quantum state ρ, the classical shadow method applies a unitary UQ uniformly randomly sampled from matchgate group \({{\mathbb{M}}}_{n}\), followed by measuring the generated state in the computational basis. With the measurement result \(\left.\left\vert x\right\rangle \!\right\rangle\), we can generate the classical representation \(\hat{\rho }={{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{Q}^{{\dagger} }\left.\left\vert x\right\rangle \!\right\rangle\) for the unknown quantum state ρ, where the channel \({{{\mathcal{M}}}}\) describing the overall process is defined as

$$\begin{array}{rc}{{{\mathcal{M}}}}(\rho )&={\int}_{Q}d\mu (Q)\left[\mathop{\sum}\limits_{x\in {\left\{0,1\right\}}^{n}}\left\langle x| {U}_{Q}\rho {U}_{Q}^{{\dagger} }| x\right\rangle {U}_{Q}^{{\dagger} }\left\vert x\right\rangle \,\left\langle x\right\vert {U}_{Q}\right]\\ &=\mathop{\sum}\limits_{k}\frac{\left(\begin{array}{l}n\\ k\end{array}\right)}{\left(\begin{array}{l}2n\\ 2k\end{array}\right)}{{{{\mathcal{P}}}}}_{2k}(\rho ).\end{array}$$
(4)

Noise assumptions

In this work, we assume that the noise is gate-independent, time-independent, and Markovian (a common assumption in randomized benchmarking (RB) abbreviated as the GTM noise assumption40) and that the preparation noise for the easily prepared state \(\left\vert {{{\boldsymbol{0}}}}\right\rangle \,\left\langle {{{\boldsymbol{0}}}}\right\vert\) is negligible. For the convenience of calculation, we utilize the left-hand side noisy representation for a noisy fermionic unitary \({\widetilde{{{{\mathcal{U}}}}}}_{Q}:= {{\Lambda }}{{{{\mathcal{U}}}}}_{Q}\). Here we define the average fidelity in Γ2k subspace for noise channel Λ as

$${{{{\mathcal{B}}}}}_{k}:= \frac{{(-i)}^{k}}{{2}^{n}(\begin{array}{l}n\\ k\end{array})}\mathop{\sum}\limits_{x}\mathop{\sum}\limits_{S\in \left(\begin{array}{l}[n]\\ k\end{array}\right)}{(-1)}^{{x}_{S}}{{{\rm{Tr}}}}\left(\left\vert x\right\rangle \,\left\langle x\right\vert {{\Lambda }}({\gamma }_{D(S)})\right),$$
(5)

where \(D(S)=\left\{2j-1,2j| j\in S\right\},0\le k\le n,{x}_{S}={\sum }_{j\in S}{x}_{j}\). It is easy to check that \({{{{\mathcal{B}}}}}_{k}=1\) if k = 0. With some calculations, we have \({{{{\mathcal{B}}}}}_{k}=1\) for the noise-free model where noise channel Λ equals the identity. In the following, we give the analysis of the simplified result for \({{{{\mathcal{B}}}}}_{k}\) for several common noise models in the qubit system and fermionic system when k > 1. See more details for the analysis in Supplementary Note 3.

(1) The depolarizing noise with channel representation \({{{\Lambda }}}_{{{{\rm{d}}}}}(A)=(1-p)A+p{{{\rm{Tr}}}}\left(A\right)\frac{{\mathbb{I}}}{{2}^{n}}\) for any n-qubit linear operator A, where the noise strength p ∈ [0, 1], and \({{{{\mathcal{B}}}}}_{k}=1-p\).

(2) The generalized amplitude-damping noise with the Kraus representation

$$\begin{array}{r}{{{\Lambda }}}_{{{{\rm{a}}}}}(\cdot )=\mathop{\sum}\limits_{\begin{array}{c}u,v\in {\left\{0,1\right\}}^{n}\\ u\ne v\end{array}}{E}_{uv}(\cdot ){E}_{uv}^{{\dagger} }+{E}_{0}(\cdot ){E}_{0}^{{\dagger} },\end{array}$$
(6)

where \({E}_{uv}=\sqrt{\bar{{p}_{u}}}\left\vert v\right\rangle \,\left\langle u\right\vert\) for u ≠ v ∈ {0, 1}n and \({E}_{0}=\sqrt{{\mathbb{I}}-{\sum }_{\begin{array}{c}u,v\in {\left\{0,1\right\}}^{n}\\ u\ne v\end{array}}{E}_{uv}^{{\dagger} }{E}_{uv}}\), where the probabilities \({\bar{p}}_{u}\) satisfy \(({2}^{n}-1){\bar{p}}_{u}\le 1\) for any \(u\in {\left\{0,1\right\}}^{n}\). The average fidelity \({{{{\mathcal{B}}}}}_{k}=1-{\sum }_{u\in {\left\{0,1\right\}}^{n}}{\bar{p}}_{u}\) if k ≠ 0. We let \({\sum }_{u\in {\left\{0,1\right\}}^{n}}{\bar{p}}_{u}\) denote the noise strength.

(3) The X-rotation noise with the channel representation

$$\begin{array}{r}{{{\Lambda }}}_{{{{\rm{r}}}}}(\cdot )={R}_{X}({{{\boldsymbol{\theta }}}})(\cdot ){R}_{X}(-{{{\boldsymbol{\theta }}}})\end{array}$$
(7)

where \({R}_{X}({{{\boldsymbol{\theta }}}})=\exp (-i\mathop{\sum }\nolimits_{l = 1}^{n}{\theta }_{l}{X}_{l}/2)\), where the noise strengths θl are some real numbers. By some calculations, we have \({{{{\mathcal{B}}}}}_{k}={(\begin{array}{l}n\\ k\end{array})}^{-1}{\sum }_{S\in (\begin{array}{l}[n]\\ k\end{array})}{\prod }_{l\in S}\cos {\theta }_{l}\). Hence \(\mathop{\min }\limits_{l}{\cos }^{k}{\theta }_{l}\le {{{{\mathcal{B}}}}}_{k}\le \mathop{\max }\limits_{l}{\cos }^{k}{\theta }_{l}\).

(4) Noise that is a Gaussian unitary41,42, where we assume that the noise has no coherence with the environment. This noise channel is denoted as

$$\begin{array}{r}{{{\Lambda }}}_{{{{\rm{g}}}}}(\cdot )={U}_{Q}(\cdot ){U}_{Q}^{{\dagger} },\end{array}$$
(8)

where UQ is a Gaussian unitary. By selecting the noise model to be Λg, we get \({{{{\mathcal{B}}}}}_{k}={(\begin{array}{l}n\\ k\end{array})}^{-1}{\sum }_{S,{S}^{{\prime} }\in (\begin{array}{l}[n]\\ k\end{array})}\det (Q{| }_{D(S),D({S}^{{\prime} })})\).

Note that for the noise models defined in (1–3), the average fidelity \({{{{\mathcal{B}}}}}_{k}\in [0,1]\) is close to one when the noise strengths are close to zero.

For comparison, it is worth noting that the standard average noise fidelity43\({F}_{{{{\rm{avg}}}}}={\int}_{\psi }d\psi \left\langle \psi | {{\Lambda }}(\left\vert \psi \right\rangle \left\langle \psi \right\vert )| \psi \right\rangle\) where ψ is drawn from the Haar measure, and the Z-basis average noise fidelity defined in Chen et al.29, \({F}_{Z}=\frac{1}{{2}^{n}}{\sum }_{b}\left\langle \!\langle b| {{\Lambda }}| b\rangle \!\right\rangle\) are not equivalent to \({{{{\mathcal{B}}}}}_{k}\) under the same noise model. We present a comparison of these three quantities for Λd, Λa, Λr for a single qubit, as depicted in Table 2. They are closely aligned, with \({{{{\mathcal{B}}}}}_{1}\) slightly smaller than Favg and FZ. We give a more detailed analysis in Supplementary material X.

Table 2 Comparison of average noise fidelity Fave, Z-basis average noise fidelity FZ, and average noise fidelity in Γ2k subspace \({{{{\mathcal{B}}}}}_{k}\)
Full size table

Mitigation algorithm and error analysis

Let \(\widehat{{{{\mathcal{M}}}}}:= \mathop{\sum }\nolimits_{k = 0}^{n}{\hat{f}}_{2k}{{{{\mathcal{P}}}}}_{2k}\) be the estimator for the noisy shadow channel \(\widetilde{{{{\mathcal{M}}}}}=\mathop{\sum }\nolimits_{k = 0}^{n}{f}_{2k}{{{{\mathcal{P}}}}}_{2k}\). In the Methods Section, we provide an explicit expression and efficiency for the calculation of \({\hat{f}}_{2k}\). Using the estimated noisy channel \(\widehat{{{{\mathcal{M}}}}}\), we can now obtain an estimate for \({\{{{{\rm{Tr}}}}(\rho {H}_{j})\}}_{j = 1}^{m}\), where ρ represents certain quantum states and Hj denotes certain observables. If f2k = 0, the channel \(\widetilde{{{{\mathcal{M}}}}}\) becomes non-invertible. Consequently, the effectiveness of the fermionic CS method diminishes, and we cannot retrieve \({{{\rm{tr}}}}(\rho H)\) using it. In this study, we operate under the assumption that the noise is permissible and the fermionic CS channel is consistently invertible. Additionally, we provide a scenario in Supplementary Note 3 where the extreme noise channel occurs, i.e., fk = 0. However, it is anticipated that such an extreme case will rarely occur. Algorithm 1 demonstrates the method for mitigated estimation.

Algorithm 1

Error-mitigated estimation for noisy fermionic classical shadows

1: Input Quantum state ρ, observables H1, …, Hm, integers Nc, Kc, Ne, Ke.

2:  Output\({\hat{v}}_{i}\) for i ∈ [m].

3:  Rc ≔ NcKc;

4:  for j ← 1 to Rc do

5: Prepare state \({\rho }_{0}=\left\vert {0}^{n}\right\rangle\), uniformly sample Q ∈ Orth(2n) or Perm(2n), implement the associated noisy Gaussian unitary \({\widehat{U}}_{Q}\) on ρ0, and measure in the Z-basis with outcomes x;

6: Let \({\hat{f}}_{2k}^{(j)}:= {2}^{n}{(-1)}^{k}{\left(\begin{array}{l}n\\ k\end{array}\right)}^{-1}\langle \!\langle {{{\bf{0}}}}| {{{{\mathcal{P}}}}}_{2k}{{{{\mathcal{U}}}}}_{Q}^{{\dagger} }| x\rangle \!\rangle ,\forall k\in [n]\);

7: end for

8: \({\hat{f}}_{2k}:= \,{{{\bf{MedianOfMeans}}}}\,\left({\left\{{f}_{2k}^{(j)}\right\}}_{j = 1}^{{R}_{c}},{N}_{c},{K}_{c}\right)\forall k\in [n]\);

9: \(\widehat{{{{\mathcal{M}}}}}:= \mathop{\sum }\nolimits_{k = 1}^{n}{\hat{f}}_{2k}{{{{\mathcal{P}}}}}_{2k}\);

10: Re ≔ NeKe;

11:  for i ← 1 to m do

12:  for j ← 1 to Re do

13: Prepare ρ, uniformly sample Q ∈ O(2n) or Perm(2n), implement the associated noisy Gaussian unitary \({\hat{U}}_{Q}\) on ρ, and measure in the Z-basis with outcomes x;

14: Generate estimation \({\hat{v}}_{i}^{(j)}:= {{{\rm{Tr}}}}\left({H}_{i}{\widehat{{{{\mathcal{M}}}}}}^{-1}{{{{\mathcal{U}}}}}_{Q}^{{\dagger} }(x)\right)\);

15:  end for

16: \({\hat{v}}_{i}:= {{{\bf{MedianOfMeans}}}}\,\left({\left\{{\hat{v}}_{i}^{(j)}\right\}}_{j = 1}^{{R}_{e}},{N}_{e},{K}_{e}\right)\);

17: end for

18: return \({\left\{{\hat{v}}_{i}\right\}}_{i = 1}^{m}\)

Incorporating the MedianOfMeans sub-procedure, as explained in Ref. 9, guarantees that the number of quantum state copies needed relies on the logarithm of the number of observables. We included the MedianOfMeans sub-procedure in Supplementary Note 6 to ensure the completeness and consistency of this paper. Our error analysis will involve selecting appropriate values for the number of calibrations and estimation samplings Nc, Ne, Kc, and Ke to estimate the coefficients \({\hat{f}}_{2k}\) associated with the noisy channel.

Let \(\hat{v}:= {{{\rm{Tr}}}}({\widehat{{{{\mathcal{M}}}}}}^{-1}{{{{\mathcal{U}}}}}^{{\dagger} }(\left\vert x\right\rangle \,\left\langle x\right\vert )H)\) be an estimation of \({{{\rm{Tr}}}}\left(\rho H\right)\) for some observables H in the even subspace Γeven and quantum states ρ, where x follows the distribution \({{{\rm{Tr}}}}\left(\left\vert x\right\rangle \,\left\langle x\right\vert \widehat{{{{\mathcal{U}}}}}(\rho )\right)\) for \(x\in {\left\{0,1\right\}}^{n}\), then we have

$$\begin{array}{l}\left\vert \hat{v}-{{{\rm{Tr}}}}\left(\rho H\right)\right\vert \,\le \left\vert \hat{v}-{{{\rm{Tr}}}}\left({\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}\left(\rho \right)H\right)\right\vert \\ \qquad\qquad\qquad+\left\vert {{{\rm{Tr}}}}\left({\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}\left(\rho \right)H\right)-{{{\rm{Tr}}}}\left(\rho H\right)\right\vert \\ \qquad\qquad\qquad={\varepsilon }_{e}+{\varepsilon }_{c},\end{array}$$
(9)

where \({\varepsilon }_{e}:= \left\vert \hat{v}-{{{\rm{Tr}}}}\left({\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}(\rho )\right)\right\vert\) is the estimation error and \({\varepsilon }_{c}:= \left\vert {{{\rm{Tr}}}}\left({\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}\left(\rho \right)H\right)-{{{\rm{Tr}}}}\left(\rho H\right)\right\vert\) is the calibration error. Therefore, by determining the necessary number of samples Ne and Ke to achieve the desired level of estimation error εe (as well as Nc and Kc to account for the calibration error εc), we can obtain an estimation \(\hat{v}\) with an overall error of ε = εe + εc, using NeKe copies of the input state ρ.

Theorem 1

Let ρ be an unknown quantum state and \({\left\{{H}_{i}\right\}}_{i = 1}^{m}\) be a set of observables in the even subspace Γeven. Consider Algorithm 1 with the number of estimation samplings

$$\begin{array}{ll}{R}_{e}\,=\frac{68{(1+{\varepsilon }_{c})}^{2}\ln (2m/{\delta }_{e})}{{2}^{2n}{\varepsilon }_{e}^{2}}\mathop{\sum}\limits_{0\le {l}_{1}+{l}_{2}+{l}_{3}\le n}g({l}_{1},{l}_{2},{l}_{3})\\ \,\mathop{\sum}\limits_{\tiny{\begin{array}{c}{S}_{1},{S}_{2},{S}_{3}\,{{{\rm{disjoint}}}}\atop | {S}_{i}| =2{l}_{i}\forall i\in [3]\end{array}}}{{{\rm{Tr}}}}\left({\widetilde{\gamma }}_{{S}_{1}}{\widetilde{\gamma }}_{{S}_{2}}{H}_{0}\right){{{\rm{Tr}}}}\left({\widetilde{\gamma }}_{{S}_{2}}{\widetilde{\gamma }}_{{S}_{3}}{H}_{0}\right){{{\rm{Tr}}}}\left({\widetilde{\gamma }}_{{S}_{3}}{\widetilde{\gamma }}_{{S}_{1}}\rho \right),\end{array}$$

where \(g({l}_{1},{l}_{2},{l}_{3})=\frac{{(-1)}^{{l}_{1}+{l}_{2}+{l}_{3}}{\left(\begin{array}{l}n\\ {l}_{1},{l}_{2},{l}_{3}\end{array}\right)}_{p}\left(\begin{array}{l}2n\\ 2{l}_{1}+2{l}_{2}\end{array}\right)\left(\begin{array}{l}2n\\ 2{l}_{2}+2{l}_{3}\end{array}\right){{{{\mathcal{B}}}}}_{{l}_{1}+{l}_{3}}}{{\left(\begin{array}{l}2n\\ 2{l}_{1},2{l}_{2},2{l}_{3}\end{array}\right)}_{p}\left(\begin{array}{l}n\\ {l}_{1}+{l}_{2}\end{array}\right)\left(\begin{array}{l}n\\ {l}_{2}+{l}_{3}\end{array}\right){{{{\mathcal{B}}}}}_{{l}_{1}+{l}_{2}}{{{{\mathcal{B}}}}}_{{l}_{2}+{l}_{3}}}\), and \({H}_{0}=\mathop{\max }\limits_{i}({H}_{i}-{{{\rm{Tr}}}}\left({H}_{i}\right)\frac{{\mathbb{I}}}{{2}^{n}})\), and the number of calibration samplings

$${R}_{c}={{{\mathcal{O}}}}\left(\frac{{{{{\mathcal{B}}}}}_{\max }\sqrt{n}\ln n\ln (1/{\delta }_{c})}{{{{{\mathcal{B}}}}}_{\min }^{2}{\varepsilon }_{c}^{2}}\right),$$

where \({{{{\mathcal{B}}}}}_{\max }=\mathop{\max }\limits_{k}\left\vert {{{{\mathcal{B}}}}}_{k}\right\vert\) and \({{{{\mathcal{B}}}}}_{\min }=\mathop{\min }\limits_{k}\left\vert {{{{\mathcal{B}}}}}_{k}\right\vert\). Then, the outputs \({\left\{{v}_{i}\right\}}_{i = 1}^{m}\) of the algorithm approximate \({\left\{{{{\rm{Tr}}}}\left(\rho {H}_{i}\right)\right\}}_{i = 1}^{m}\) with error εe + εc and success probability 1 − δe − δc, under the assumption that \({\left\Vert {H}_{i}\right\Vert }_{\infty }={{{\mathcal{O}}}}\left(1\right)\), where \({\left\Vert {H}_{i}\right\Vert }_{\infty }\) is the spectral norm of Hi.

We observe that the sampling for estimation we obtained is consistent with Wan et al.28 in the absence of noise. In the following, we will provide an analysis of the necessary number of measurements to compute \({\left\langle \right.}^{{{{\boldsymbol{k}}}}}\left.{{{\bf{D}}}}\right\rangle\) using Algorithm 1. To calculate the representation of each element \({{\left\langle \right.}^{{{{\boldsymbol{k}}}}}\left.{{{\bf{D}}}}\right\rangle }_{{j}_{1},\ldots ,{j}_{k};{l}_{1},\ldots ,{l}_{k}}\), where ji, li are in the range [n] for i ∈ [k], we need to calculate \(m={{{\mathcal{O}}}}\left({n}^{k}\right)\) expectations for different \({\widetilde{\gamma }}_{S}\), where \(\left\vert S\right\vert =2k\). By choosing the observable \({H}_{j}={\widetilde{\gamma }}_{S}\) where \(\left\vert S\right\vert =2k\) and \(m={{{\mathcal{O}}}}\left({n}^{k}\right)\) in Theorem 1, with the number of estimation samplings

$${R}_{e}={{{\mathcal{O}}}}\left(\frac{k{n}^{k}\ln (n/{\delta }_{e})}{{{{{\mathcal{B}}}}}_{k}^{2}{\varepsilon }_{e}^{2}}\right)$$
(10)

and the number of calibration samplings

$${R}_{c}={{{\mathcal{O}}}}\left(\frac{{{{{\mathcal{B}}}}}_{\max }\sqrt{n}\ln n\ln (1/{\delta }_{c})}{{{{{\mathcal{B}}}}}_{\min }^{2}{\varepsilon }_{c}^{2}}\right),$$
(11)

the estimation error can be bounded to εe + εc. The equations for Re and Rc can be simplified to \({R}_{e}={{{\mathcal{O}}}}(\frac{k{n}^{k}\ln (n/{\delta }_{e})}{{\varepsilon }_{e}^{2}})\) and \({R}_{c}={{{\mathcal{O}}}}(\frac{\sqrt{n}\ln n\ln (1/{\delta }_{c})}{{\varepsilon }_{c}^{2}})\) for the general noises with constant average fidelity \({{{{\mathcal{B}}}}}_{k}\) in subspace Γ2k for any \(k\in \left\{0,\ldots ,n\right\}\). We give more details for the calculations in Supplementary Note 8. However, some types of noise channels, such as certain Gaussian unitary channels present in the related 2n × 2n matrix Q, cannot be mitigated with our mitigation algorithm. In particular, there exists a signed permutation matrix Q for which f2k = 0, resulting in complete loss of projection for the observable onto the subspace Γ2k. As a result, it is impossible to calculate \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\) for any set S containing 2k elements. We anticipate that the noise in the quantum device will differ significantly from the UQ which belongs to the intersection of the matchgate and Clifford groups.

Numerical results

Here we give the numerical results for the mitigated shadow estimation in the fermionic systems. Since the elements of a k-RDM can be expressed in the form \({{{\rm{Tr}}}}\left(\rho {\gamma }_{S}\right)\), we give the numerical results of the errors of the estimators for the expectation value of local fermionic observables \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\).

The estimator \(\hat{v}\) for \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\) can be represented as in Eq. (17). Here we choose the number of qubits n = 4 and \(S=\left\{1,2\right\}\), and \({\widetilde{\gamma }}_{S}={U}_{Q}^{{\dagger} }{\gamma }_{S}{U}_{Q}\) and Q is uniformly randomly chosen from Perm(2n). The quantum state ρ is a uniformly randomly generated 4-qubit pure state. As shown in Fig. 1, we depict the estimations of classical shadow estimators28 and our mitigated Algorithm 1, with the changes of noise strength (Fig. 1a–d) and the changes of the number of samples (Fig. 1e–h). Here we numerically test the estimations with respect to depolarizing, amplitude damping, X-rotation, and Gaussian unitaries.

Fig. 1: The estimations for the expectation values of Majorana operators.
figure 1

The estimations with the changes of (a–d) the noise strength and (e–h) the number of samples for fixed noise parameters, where (a, e) are associated with depolarizing noise, (b, f) are associated with generalized amplitude damping noise, (c, g) are associated with X-rotation noise, (d, h) are associated with Gaussian unitary noise. The error bar is the estimation of the standard deviation by repeating the procedure for R = 10 rounds, and it is estimated to be \(\sqrt{\mathop{\sum }\nolimits_{i = 1}^{R}{({\hat{v}}_{i}-\bar{v})}^{2}/R}\), where \(\bar{v}\) is the expectation of the corresponding estimations. Specially, \(\bar{v}=\frac{{f}_{| S| }}{g}{{{\rm{Tr}}}}\left(\rho {\gamma }_{S}\right)\), \(g={\hat{f}}_{\left\vert S\right\vert }\) for Mitigated estimation, and \(g=\frac{{{n}\choose{k/2}}}{{{2n}\choose{k}}}\) for CS estimation. In (a–d), the x-axis represents the labels for different noise parameters. The dotted horizontal line indicates the value \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\).

Full size image

The calibration samples in Algorithm 1 for the numerics are Nc = 4, 000 and Kc = 20 for all noise models. The number of samples for the classical shadow method is set as Ne = 4, 000, Ke = 10, and for Algorithm 1 are set as Ne = 4, 000/(1 − pnoise) and Ke = 10, where pnoise is the noise strength varying for different noise settings:

  1. (1)

    Depolarizing noise \({{{\Lambda }}}_{{{{\rm{d}}}}}(\rho )=(1-p)\rho +p\frac{{\mathbb{I}}}{{2}^{n}}\), where ρ is any quantum state and p is the depolarizing noise strength. In Fig. 1a, p varies from 0.05 to 0.3 (p = 0.05j for x-axis equals j where j ∈ [6]), and in Fig. 1 (b), p = 0.2.

  2. (2)

    Generalized amplitude damping noise Λa with representation

    $${{{\Lambda }}}_{{{{\rm{a}}}}}(\rho )=\mathop{\sum}\limits_{\displaystyle{u,v\in {\left\{0,1\right\}}^{n}\atop u\ne v}}{E}_{uv}\rho {E}_{uv}^{{\dagger} }+{E}_{0}\rho {E}_{0}^{{\dagger} },$$
    (12)

    where \({E}_{uv}=\sqrt{{p}_{uv}}\left\vert v\right\rangle \,\left\langle u\right\vert\) for u ≠ v ∈ {0, 1}n and \({E}_{0}=\sqrt{{\mathbb{I}}-{\sum }_{\begin{array}{c}u,v\in {\left\{0,1\right\}}^{n}\\ u\ne v\end{array}}{E}_{uv}^{{\dagger} }{E}_{uv}}\). Note that Eq. (12) is a generalization of Eq. (6), which connects to Eq. (6) by setting \({p}_{uv}={\bar{p}}_{u}\) for any u, v ∈ [n]. Here we uniformly randomly choose puv in \(\frac{[0,1]+j-1}{6\times {2}^{n+1}}\), and labeled it as j in the x-axis of Fig. 1 where j ∈ [6], and choose the generated damping errors for j = 5 case in Fig. 1 (b) as the damping errors for Fig. 1f.

  3. (3)

    X-rotation noise Λr defined in Eq. (7) with noise parameters \({\theta }_{j}=\frac{\pi }{2\left(8-j\right)}\) for j ∈ [6], and the noise strength is chosen as \(1-\cos \theta\) in Fig. 1c, and Fig. 1g depicts the errors in the X-rotation noise with noise parameter θ6. The x-axis of the mitigation results of X-rotation noise in Fig. 1c denotes the label for noise parameters \(\cos {\theta }_{j}\) for j range from 1 to 6.

  4. (4)

    The Gaussian unitary noise channel \({{{{\mathcal{U}}}}}_{Q}\) is chosen such that Q is sampled from the signed permutation group, ensuring that the coefficient f1 for the noise channel is non-zero. The associated numerical results are shown in Fig. 1d, h. The number of estimation samplings Ne = 8000, Ke = 10 for Fig. 1d. Fig. 1h choose the same noise parameter with the fifth noise parameter in Fig. 10d. From the figure, we see that without mitigation, the error is enormous with the CS algorithm.

In Fig. 1e–h the number of samples ranges from \(\left\lfloor 900+100\exp (j)\right\rfloor\) for \(j\in \left\{0,\ldots ,5\right\}\). From Fig. 1, we see that with the increase of the noise strength, the classical shadow method with depolarizing, amplitude damping, and X-rotation noise all gradually diverge to the expected value \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\), while our error-mitigated estimation protocol in Alg. 1 gives an expected value that is close to the noiseless value. Based on the numerical results depicted in Fig. 1e–h, it is evident that as the number of samples increases, the estimation outcomes generated by Algorithm 1 approaches the expected value \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\), while the convergent value for the classical shadow method is far from the expected value with depolarizing, amplitude damping, and X-rotation noises. Conversely, the error bar associated with CS estimations is observed to be smaller compared to mitigated estimations, using the same number of samplings, as illustrated in Fig. 1e–h. This is due to the variance of the mitigated estimations associated with the average noise fidelities in Γ2k subspace \({{{{\mathcal{B}}}}}_{k}\).

Discussion

We present an error-mitigated classical shadow algorithm for noisy fermionic systems, thereby extending matchgate classical shadows for noiseless systems26,28. With our method, the calibration process requires a number of copies of the classical state \(\left\vert {{{\boldsymbol{0}}}}\right\rangle \,\left\langle {{{\boldsymbol{0}}}}\right\vert\) that scales logarithmically with the number of qubits. Assuming a constant average noise fidelity for the noise channel, our algorithm requires the same order of estimation copies as the matchgate classical shadow without error mitigation28. Our algorithm is applicable for efficiently calculating all the elements of a given k-RDM.

To provide a clearer demonstration of the average fidelity of common noises, we consider depolarizing, amplitude damping, and X-rotation noises. The average fidelity of depolarizing and amplitude damping noises are given by (1 − p) and \((1-{\sum }_{u}{\bar{p}}_{u})\) respectively, where \(p,{\bar{p}}_{u}\) are the noise parameters. For X-rotation noise, the average fidelity lies between \([\mathop{\min}\nolimits_{\theta }{\cos }^{k}\theta ,\mathop{\max }\nolimits_{\theta }{\cos }^{k}\theta ]\) where θ is the rotated angles. To evaluate the effectiveness of our algorithm in mitigating these noises, we compare its performance with the matchgate CS algorithm to calculate the expectations of \({\widetilde{\gamma }}_{S}\), where \(\left\vert S\right\vert =2k\), which is crucial for calculating k-RDMs. Our numerical results show good agreement with the theory, validating the effectiveness of our algorithm.

While our algorithm demonstrates good performance in the presence of common types of noise in near-term quantum devices, further investigations are required to explore its potential limitations and improvements. Some of the open questions that can be addressed in future research include:

  1. (1)

    Is it possible to extend our algorithm to handle other types of noise, such as time-dependent, non-Markovian and environmental noise44, or more generally, noise that does not satisfy the GTM assumption? If so, how would these different types of noise impact the performance of our algorithm?

  2. (2)

    We provide numerical results under the assumption of Gaussian unitary noise, a common noise model in the fermionic platform. An intriguing unanswered question pertains to the performance of our algorithm in the presence of more typical noise channels inherent to fermionic platform.

  3. (3)

    The number of gates required by the matchgate circuit is \({{{\mathcal{O}}}}({n}^{2})\)45. As a result, the accumulation of noise significantly increases the error mitigation threshold46,47, which raises the intriguing question of whether it is feasible to provide an error-mitigated classical shadow using a shallower circuit. This may be compared with Bertoni et al.48, who propose a shallower classical shadow approach for qubit systems.

  4. (4)

    In addition, we have included in the Supplementary materials the analysis and numerical results regarding the overlap between a Gaussian state and any quantum states, as well as the inner product between a Slater determinant and any pure state. This prompts the question of whether our algorithm can be utilized to calculate other physical, chemical, or material properties beyond the scope of this paper.

Exploring these questions would enhance our comprehension of the potential and limitations of our algorithm, and could potentially pave the way for advancements in the estimation of fermionic Hamiltonian expectation values with near-term quantum devices.

Note added

Following the completion of our manuscript, we became aware of recent independent work by Zhao and Miyake49, who also study ways to counteract noise in the fermionic shadows protocol.

Methods

Noisy fermionic channel representation

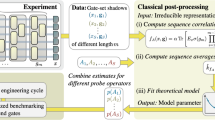
Here we present an unbiased estimation approach for the noisy representation of the fermionic shadow channel, which utilizes a protocol similar to the matchgate benchmarking protocol50. According to representation theory51 (see details in Supplementary Note 1), the noisy fermionic shadow channel can be represented as \(\widetilde{{{{\mathcal{M}}}}}=\mathop{\sum }\nolimits_{k = 0}^{n}{f}_{2k}{{{{\mathcal{P}}}}}_{2k}\). Since \({{{\rm{Tr}}}}(H\widetilde{{{{\mathcal{M}}}}}(\rho ))={{{\rm{Tr}}}}(\rho \widetilde{{{{\mathcal{M}}}}}(H))\), with the pre-knowledge of f2k we can calculate \({{{\rm{Tr}}}}(H\widetilde{{{{\mathcal{M}}}}}(\rho ))\) for any observable H in the even subspace. To learn the 2(n + 1) coefficients, we begin with the easily prepared state \({\rho }_{0}=\left\vert {{{\boldsymbol{0}}}}\right\rangle \,\left\langle {{{\boldsymbol{0}}}}\right\vert\) and apply a noisy unitary channel \(\widehat{{{{\mathcal{U}}}}}\) with \({{{\mathcal{U}}}}\) sampled from the matchgate group. We then perform a Z-basis measurement \({{{\mathcal{X}}}}\) with measurement outcomes \(x\in {\left\{0,1\right\}}^{n}\), followed by classically operating the unitary channel \({{{{\mathcal{U}}}}}^{{\dagger} }\) on \(\left\vert x\right\rangle \,\left\langle x\right\vert\). The generated state has expected value \(\mathop{\sum }\nolimits_{k = 0}^{n}{f}_{2k}{{{{\mathcal{P}}}}}_{2k}({\rho }_{0})\), and f2k is obtained by projecting the final state to the \({{{{\mathcal{P}}}}}_{2k}\) subspace with some classical post-processing. We illustrate the learning process of the noisy channel in Fig. 2a. The following theorem provides an unbiased estimation of the noisy fermionic classical shadow.

Fig. 2: Schematic diagram of the error-mitigated matchgate classical shadow algorithm.
figure 2

a Protocol to learn the noisy classical shadow channel, where \(\widetilde{{{{\mathcal{M}}}}}={{{{\mathcal{U}}}}}_{Q}^{{\dagger} }\circ {{{\mathcal{X}}}}\circ {{\Lambda }}\circ {{{{\mathcal{U}}}}}_{Q}(\cdot )=\mathop{\sum }\nolimits_{k = 0}^{n}{f}_{2k}{{{{\mathcal{P}}}}}_{2k}(\cdot )\), where \({{{{\mathcal{U}}}}}_{Q}\) is uniformly randomly sampled from the matchgate group. The estimation \({\hat{f}}_{2k}\) for f2k is obtained by projecting \(\widetilde{{{{\mathcal{M}}}}}\) to \({{{{\mathcal{P}}}}}_{2k}\) subspace with input state \({\rho }_{0}=\left\vert {{{\boldsymbol{0}}}}\right\rangle \,\left\langle {{{\boldsymbol{0}}}}\right\vert\). b The shadow estimation \(\hat{\rho }\) for input state ρ with the noisy quantum circuit and classical post-processing with the approximated noisy classical shadow channel in (a), where \({{{{\mathcal{U}}}}}_{{Q}^{{\prime} }}\) is uniformly randomly sampled from the matchgate group.

Full size image

Theorem 2

The noisy fermionic shadow channel can be represented as \(\widetilde{{{{\mathcal{M}}}}}={\sum }_{k}{f}_{2k}{{{{\mathcal{P}}}}}_{2k}\), where \({{{{\mathcal{P}}}}}_{2k}\) is defined in Eq. (1), and \({\hat{f}}_{2k}={2}^{n}\langle \!\langle {{{\bf{0}}}}| {{{{\mathcal{P}}}}}_{2k}{{{{\mathcal{U}}}}}_{Q}^{{\dagger} }| x\rangle \!\rangle /\left(\begin{array}{l}n\\ k\end{array}\right)\) is an unbiased estimator of \({f}_{2k}\in {\mathbb{R}}\), where \(\left.\left\vert x\right\rangle \!\right\rangle\) is the measurement outcome from the noisy shadow protocol obtained by starting from the input state \(\left.\left\vert {{{\boldsymbol{0}}}}\right\rangle \!\right\rangle\) and applying a noisy quantum circuit \({\widetilde{{{{\mathcal{U}}}}}}_{Q}\) followed by a Z-basis measurement, where \({{{{\mathcal{U}}}}}_{Q}\) is uniformly randomly picked from the matchgate group.

The representation of the noisy fermionic channel, denoted by \(\widetilde{{{{\mathcal{M}}}}}={\sum }_{k}{f}_{2k}{{{{\mathcal{P}}}}}_{2k}\), where \({f}_{2k}\in {\mathbb{C}}\), can be obtained by the irreducible representation of the Gaussian unitary. A detailed proof of this theorem is provided in Supplementary Note 4. We claim that the coefficients \({\hat{f}}_{2k}\) can be efficiently calculated with the following lemma.

Lemma 1

\({\hat{f}}_{2k}\) is the coefficient of xk in the polynomial pQ(x), where

$${p}_{Q}(x)={\left(\begin{array}{l}n\\ k\end{array}\right)}^{-1}{{{\rm{pf}}}}\left({C}_{\left\vert {{{\boldsymbol{0}}}}\right\rangle }\right){{{\rm{pf}}}}\left(-{C}_{\left\vert {{{\boldsymbol{0}}}}\right\rangle }^{-1}+x{Q}^{T}{C}_{\left\vert x\right\rangle }Q\right),$$
(13)

where \({C}_{\left\vert x\right\rangle }{ = \bigoplus }_{i = 1}^{n}\left(\begin{array}{rc}0&{(-1)}^{{x}_{j}}\\ {(-1)}^{{x}_{j}+1}&0\end{array}\right)\) is the covariance matrix of \(\left\vert x\right\rangle\).

This lemma can be obtained by Proposition 1 in Ref. 28. For the completeness of this paper, we also give the proof of this lemma in Supplementary Note 4. The coefficients can be calculated with the polynomial interpolation method in polynomial time. With Theorem 2, we can give an unbiased estimation \(\widehat{{{{\mathcal{M}}}}}\) for \(\widetilde{{{{\mathcal{M}}}}}\).

By the definition of \({\hat{f}}_{2k}\), and the twirling properties of \({\int}_{Q}d\mu (Q){{{{\mathcal{U}}}}}_{Q}^{\otimes 2}\), the expectation value for the estimation \({\hat{f}}_{2k}\) can be formulated as

$${f}_{2k}={\left(\begin{array}{l}2n\\ 2k\end{array}\right)}^{-1}\left(\begin{array}{l}n\\ k\end{array}\right){{{{\mathcal{B}}}}}_{k}.$$
(14)

We postpone the details of this proof to Supplementary Note 4. It implies that in the noiseless scenario, \(\widetilde{M}\) degenerates into \({{{\mathcal{M}}}}\) as defined in Equation (4). Combined with the definition of \({{{{\mathcal{B}}}}}_{k}\) in Eq. (5), f2k is close to \({\left(\begin{array}{l}2n\\ 2k\end{array}\right)}^{-1}\left(\begin{array}{l}n\\ k\end{array}\right)\) if the average noise fidelity in Γ2k subspace is close to one. Recall that \({{{{\mathcal{B}}}}}_{k}\) is a constant in the depolarizing, amplitude-damping, and X-rotation noises with a constant noise strength, which implies that these noises can be efficiently mitigated with our algorithm.

Alternatively, we have a counterexample in Supplementary Note 3 that illustrates the limitations of our mitigation algorithm. Specifically, if the noise follows a Gaussian unitary channel \({{{{\mathcal{U}}}}}_{Q}\) where Q is a signed permutation matrix (associated with a discrete Gaussian unitary), then \({{{{\mathcal{B}}}}}_{k}\) may become zero. Hence, f2k = 0, rendering our estimation approach unsuitable.

Recall that our goal is to estimate \({\left\{{{{\rm{Tr}}}}\left(\rho {H}_{i}\right)\right\}}_{i = 1}^{m}\) using a noisy quantum device and polynomial classical cost, where ρ is an n-qubit quantum state and Hi is an observable in the even subspace Γeven. Here we visualize the estimation process with the guarantee in Theorem 2. We uniformly randomly sample a matchgate UQ from the matchgate group and apply it to the quantum state ρ, and then measure in the Z-basis to get outcomes x. We define the estimator

$$\hat{v}={{{\rm{Tr}}}}\left(H{\widehat{{{{\mathcal{M}}}}}}^{-1}({U}_{Q}^{{\dagger} }\left\vert x\right\rangle \,\left\langle x\right\vert {U}_{Q})\right)$$
(15)
$$=\mathop{\sum }\limits_{k=0}^{n}{\hat{f}}_{2k}^{-1}{{{\rm{Tr}}}}\left(H{{{{\mathcal{P}}}}}_{2k}\left({U}_{Q}^{{\dagger} }\left\vert x\right\rangle \,\left\langle x\right\vert {U}_{Q}\right)\right).$$
(16)

It is easy to show that \({{{\rm{tr}}}}(H{\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}(\rho ))\) is an unbiased estimation of \({{{\rm{tr}}}}(\rho H)\) when \(\widetilde{{{{\mathcal{M}}}}}\) is invertible, specifically when f2k ≠ 0 for any k, and H belongs to the even subspace Γeven. Given that \({\mathbb{E}}[\widehat{{{{\mathcal{M}}}}}]=\widetilde{{{{\mathcal{M}}}}}\) and \(\hat{v}\) serves as an unbiased estimator of \({{{\rm{tr}}}}(H{\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}(\rho ))\), it implies that the estimation error \(\varepsilon := | \hat{v}-{{{\rm{tr}}}}(\rho H)|\) is bounded by \(| \hat{v}-{{{\rm{tr}}}}(H{\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}(\rho ))| +| {{{\rm{tr}}}}(H{\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}(\rho ))-{{{\rm{tr}}}}(\rho H)|\), which can be minimized with the increasing of the number of samplings for the estimations \(\hat{v}\) and \({{{\rm{tr}}}}(H{\widehat{{{{\mathcal{M}}}}}}^{-1}\widetilde{{{{\mathcal{M}}}}}(\rho ))\), as shown in Eq. (9). Note that the estimator defined in Eq. (16) is not always efficient for all states ρ and observables H. Here we claim that with this estimator, we can efficiently calculate substantial physical quantities such as the expectation value of k-RDM, which not only serves the variational quantum algorithm (VQE) of a fermionic system with up to k particle interactions52,53, but also provide supports to the calculations of derivatives of the energy54,55 and multipole moments56. It is also an indispensable resource for the error mitigation technique8,57. It also serves to calculate the overlap between a Gaussian state and any quantum state, and the inner product between a Slater determinant and any pure state inspired by the fermionic shadow analysis of Wan et al.28. We postpone the details to Supplementary Note 5.

Note that all elements of k-RDMs can be derived through \({{{\rm{Tr}}}}\left(\rho {\gamma }_{S}\right)\) for a total of \({{{\mathcal{O}}}}\left({n}^{k}\right)\) sets S with ∣S∣ = 2k. In an expansion of this concept, we now focus on evaluating \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\) for \({{{\mathcal{O}}}}\left({n}^{k}\right)\) different S with ∣S∣ = 2k. To calculate the expectation value \({{{\rm{Tr}}}}\left(\rho {\widetilde{\gamma }}_{S}\right)\), we set the input quantum state to be ρ and the observable to be \(H={\widetilde{\gamma }}_{S}\) in the estimation formula of Eq. (16), which can then be simplified to

$$\hat{v}={i}^{k}{\hat{f}}_{2k}^{-1}{{{\rm{pf}}}}\left({Q}_{1}{Q}^{T}{C}_{\left\vert x\right\rangle }Q{Q}_{1}^{T}{| }_{S}\right),$$
(17)

where \({\widetilde{\gamma }}_{j}={\sum }_{l\in [2n]}{Q}_{1}(j,l){\gamma }_{l}\), Q1(j, l) is the (j, l)-th element of Q1, and \({C}_{\left\vert x\right\rangle }{ = \bigoplus }_{i = 1}^{n}(\begin{array}{rc}0&{(-1)}^{{x}_{j}}\\ {(-1)}^{{x}_{j}+1}&0\end{array})\) is the covariance matrix of \(\left\vert x\right\rangle \,\left\langle x\right\vert\). Here, A∣S refers to the submatrix obtained by taking the columns and rows of the matrix A that are indexed by S. The simplified quantity can be calculated in polynomial time since \({\hat{f}}_{c}\) and the Pfaffian function can be calculated efficiently. We give a detailed proof of the simplification process in Supplementary Note 5.