Introduction

Imagine a scene that can play out in a science fiction movie (Fig. 1): a spaceship is helplessly falling into a black hole (BH) because its fuel supply is dwindling and does not suffice for a breakaway maneuver. Luckily, its SOS message has been received by a faraway spaceship, which is equipped with a powerful laser that can transfer coherent energy to its distressed sister ship. Unlike heat, coherent energy transfer is associated with ergotropy1,2,3,4,5,6,7,8,9,10,11 that can perform mechanical work12 to propel the ship. Unfortunately, coherent energy transfer would have poor efficiency due to diffraction and BH-gravitational lensing over large distances between the ships. Yet a revolutionary technique may still rescue the ill-fated spaceship: the laser signal can be coherently amplified in a hitherto unexplored fashion by atoms in free fall through a cavity. Namely, the amplification can only occur through the excitation of the free-falling atoms by BH Hawking radiation redirected by an orbiting mirror. The envisioned amplification can strongly enhance the coherent power transfer to the falling spaceship, providing it with enough thrust to free itself from the grip of the BH.

Fig. 1: Black-hole powered quantum coherent amplification.
figure 1

a Coherently amplified energy transfer between spaceships is enabled by a cavity filled with atoms mounted on a spaceship that is freely falling into a BH, provided the BH radiation is redirected by an orbiting mirror. b Space-time diagram of the relevant scalar modes in the Kruskal coordinates. c Schematic description of the amplification process in the cavity.

Full size image

What is the theoretical basis for this fantastic story? It is the mind-boggling idea that the Unruh vacuum13,14,15,16 yields thermal Hawking radiation near the BH horizon, but cannot directly excite atoms falling into the BH, as opposed to a bright star that can directly heat up falling atoms in its vicinity. By contrast, near a BH the free-falling atoms feel the heat only if the Hawking radiation is redirected by a mirror placed on a stable orbit around the BH (Fig. 1). Then, counter-intuitively, BH gravity can act on atoms as a heat bath, although the process is purely unitary13,14,15,16,17,18.

For atoms falling into a BH during their passage through a cavity, a perturbative (master-equation) approach maps this BH-gravitational problem onto that of a quantum heat engine that acts as a two-level maser/laser without population inversion coupled to two baths at different temperatures19. Here, the piston of the heat engine is the signal laser field, whereas the BH scalar-field modes redirected by a mirror replace the hot bath as the energy source and the cold bath as the entropy dump of the engine. This uniquely quantum mechanical manifestation of an anomalous, gravitational vacuum effect unequivocally demonstrates the validity of the thermodynamic approach to acceleration radiation near a BH. Another intriguing limit is the strong-coupling field-atom regime mediated by the BH vacuum state, an unfamiliar manifestation of gravity-induced quantum electrodynamics.

Results

Excitation of atoms by redirected Hawking radiation

A cloud of two-level atoms (TLA) initially in their ground state, is freely falling towards the BH through a cavity. The TLA is coupled to the gravitational field of the BH by a quantized scalar field13,14,15,16

$$\hat{\Phi }({\overrightarrow{r}},t)=\mathop{\sum}\limits_{i}\left[{\hat{a}}_{i}{\phi }_{i}(\overrightarrow{r},t)+H.c.\right],$$
(1)

where H.c. stands for the Hermitian conjugate, index i labels the field modes, \(\overrightarrow{r}=(r,\Theta )\) denotes the radial and angular coordinates, and \({\hat{a}}_{i}\) is the ith mode annihilation operator.

The scalar field is coupled with the TLA as depicted in the space-time diagram (Fig. 1b). An atom freely falling into a non-rotating BH while still above the horizon can (see “Mode functions of photons resonant with free-falling atoms”) be resonant with the following scalar-field modes (in the Kruskal-Szekeres coordinates)

$${\phi }_{1\Omega }(T,X)={e}^{-i\Omega \left(T-X\right)},$$
(2)
$${\phi }_{2\Omega }(T,X)={\left(T+X\right)}^{-i\Omega }\theta (T+X),$$
(3)

where θ is the step function and Ω > 0. From the perspective of the free-falling atom, the modes (2)–(3) harmonically oscillate as a function of the atom’s proper time with positive frequency. The form of the outgoing mode (2) and the ingoing mode (3) derived here (see “Mode functions of photons resonant with free-falling atoms”) is, as shown below, key to our ability to employ the BH as a source of useful quanta.

The free-falling atoms may resonantly interact with the outgoing plane-wave field ϕ1Ω and with the ingoing Rindler field ϕ2Ω. However, in the Unruh vacuum, which by consensus represents the state of the evaporating BH field16, there are no photons in the modes (2) and (3). Consequently, free-falling atoms cannot become excited in the Unruh vacuum (see “Mode functions of photons resonant with free-falling atoms”).

Instead, we might consider exciting these atoms by the outgoing Rindler photons, which fill the Unruh vacuum and constitute the Hawking radiation20,21. They thermally populate the modes

$${\phi }_{3\Omega }(T,X)={\left(X-T\right)}^{i\Omega }\theta (X-T).$$
(4)

Yet, it can be shown (“Mode functions of photons resonant with free-falling atoms”) that these outgoing Rindler photons cannot excite free-falling atoms. Is there another way to excite these atoms by BH radiation?

Indeed, there is: we show that free-falling atoms can be excited by redirecting the outgoing Rindler photons (Hawking radiation) towards the BH via a mirror. The mirror should orbit the BH at a fixed radius r = r0. To be stable, the mirror orbit should lie at r > 3rg, rg being the gravitational radius, but otherwise the value of r does not affect the result (see below). In the presence of such a mirror, the mode function satisfying the boundary condition ϕ(t, r0) = 0 at the mirror surface acquires an advantageous form

$$\phi (T,X)=\underbrace{\left(X-T\right)^{i\Omega }}_{{\phi }_{c}\,{{{\rm{mode}}}}}-\underbrace{{e}^{i\Omega \left({r}_{0}+\ln ({r}_{0}-1)\right)}{\left(T+X\right)}^{-i\Omega }}_{{\phi }_{h}{{{\rm{mode}}}}}.$$
(5)

This hitherto unexplored scalar-field mode has two parts: the outgoing Rindler photon mode (the first term on the rhs) and a part reflected from the mirror into the ingoing Rindler mode (the second term on the rhs). This ingoing Rindler mode acts as a hot bath mode, denoted as ϕh(r, t) with frequency Ω = Ωh, that can excite the free-falling atom. The outgoing Rindler modes act as a cold-bath (vacuum state) mode denoted as ϕc(r, t).

We wish to show that the redirected Hawking radiation can enable coherent amplification of a signal mode. The complete field-atom interaction Hamiltonian has then the form

$${H}_{int}=\mathop{\sum}\limits_{i}{g}_{hi}{\phi }_{hi}{\hat{b}}^{{\dagger} }{\hat{a}}_{hi}\left\vert e\right\rangle \langle g| +\mathop{\sum}\limits_{j}{g}_{cj}{\phi }_{cj}{\hat{c}}_{cj}| e\rangle \langle g\vert +H.c.$$
(6)

Here \(\hat{b}\) stands for the signal-mode annihilation operator, \({\hat{a}}_{hi}\) is the ith mode annihilation operator of the hot bath mode ϕhi of the redirected Hawking radiation, and \({\hat{c}}_{j}\) for that of the j-th cold-bath mode ϕcj of the redirected Hawking radiation (Eq. (5)).

The atom-scalar-field interaction (first term on the rhs of Eq. (6)) represents an anti-resonant Raman process whereby a scalar-field quantum in the i-th redirected Hawking-radiation mode ϕhi is converted into a signal photon by the atomic transition between the ground (g) and excited (e) states, with coupling strength ghi. The interaction Hamiltonian of the atom with the cold bath ϕcj involves the same atomic transition operator \(\left\vert e\right\rangle \left\langle g\right\vert\) with coupling strength gcj. Our goal is to maximize the energy gain of the signal mode in a non-passive (ergotropy-carrying) form, capable of delivering work12.

Strong TLA-BH coupling

Here, we assume that while traversing the cavity, the atom is strongly coupled to one redirected Hawking-radiation mode ϕh with a coupling strength gh that overwhelms the coupling strengths gcj to all cold-bath modes, i.e., gh > > gcj. This is justified if the frequency ωc of the high-Q cavity mode is taken to be off-resonant with the cold-bath mode frequencies, Ωcj, i.e., the detunings ∣Ωcj − ωc∣ are large, so that we can neglect the couplings with the cold-bath modes. This scenario corresponds to a high-Q cavity with strong coupling of a single Hawking-radiation mode to the atom. To render the problem single-mode, we choose the TLA resonant frequency ω0, the cavity frequency ωc, the signal ν and the Ωh frequency of the redirected mode ϕh in (5) such that Ωh ≈ ν + ω0 ≈ ωc. Then, the interaction Hamiltonian in Eq. (6) simplifies to

$${H}_{int}={g}_{h}{\phi }_{h}{\hat{b}}^{{\dagger} }{\hat{a}}_{h}\left\vert e\right\rangle \langle g\vert +H.c.$$
(7)

The basis for the combined atom-field energy states can then be

$$\begin{array}{rcl}\left\vert 1\right\rangle &=&\left\vert g,{n}_{s},{n}_{h}\right\rangle ,\\ \left\vert 2\right\rangle &=&\left\vert e,{n}_{s}+1,{n}_{h}-1\right\rangle ,\end{array}$$
(8)

where \(\left\vert {n}_{s}\right\rangle\) and \(\left\vert {n}_{h}\right\rangle\) are Fock states of the signal mode and the BH ϕh mode, respectively. At short times, where first-order transitions between the atom and the field modes predominate, the subspace in Eq. (8) is decoupled from other subspaces, whilst keeping the total number of excitations constant.

Let us assume that the atom and the signal mode are initially in the ground and Fock state \(\left\vert {n}_{s}\right\rangle\) respectively. Then, the initial state of the combined system in general is \({\rho }^{i}=\left\vert g\right\rangle \langle g| \otimes | {n}_{s}\rangle \left\langle {n}_{s}\right\vert \otimes {\rho }_{{T}_{c}}\otimes {\rho }_{{T}_{h}}\), where \({\rho }_{{T}_{c}}\) and \({\rho }_{{T}_{h}}\) are the cold and hot bath states at temperature Tc and Th, respectively. In this problem, Tc = 0, since, as noted above, the outgoing Rindler modes are in a Minkowski vacuum state that cannot impart photons to the free-falling atom and hence act as zero temperature bath. The initial state is then a mixture of the pure states \(\left\vert g\right\rangle \left\vert {n}_{s}\right\rangle \left\vert {n}_{h}\right\rangle\) with probabilities \({p}_{{n}_{h}}={e}^{-{\beta }_{h}{\Omega }_{h}{n}_{h}}/{Z}_{{\beta }_{h}}\), where \({\beta }_{h}=\frac{1}{{k}_{B}{T}_{H}}\) is the effective BH (Hawking) temperature20,21. A general analysis of amplification in this regime that allows for non-zero cold-bath temperature (Supplementary note (SN) 1) does not offer conceptually different physics.

The final states of the atom and the signal mode after their unitary evolution over time t are then (SN 1)

$${\rho }_{atom}^{f}=| u{| }^{2}\left\vert g\right\rangle \langle g| +| v{| }^{2}| e\rangle \left\langle e\right\vert ,$$
$${\rho }_{s}^{f}=| u{| }^{2}\left\vert {n}_{s}\right\rangle \langle {n}_{s}| +| v{| }^{2}| {n}_{s}+1\rangle \left\langle {n}_{s}+1\right\vert$$
(9)

where

$$u={e}^{-\frac{1}{2}i\delta t}(\cos (\frac{1}{2}t\sqrt{{\delta }^{2}+4{{{{\rm{g}}}}}_{h}^{2}{\phi }_{h}^{2}})+\frac{i\delta \sin (\frac{1}{2}t\sqrt{{\delta }^{2}+4{{{{\rm{g}}}}}_{h}^{2}{\phi }_{h}^{2}})}{\sqrt{{\delta }^{2}+4{{{{\rm{g}}}}}_{h}^{2}{\phi }_{h}^{2}}}),$$
$$v=-\frac{2i{{{{\rm{g}}}}}_{h}{\phi }_{h}{e}^{-\frac{1}{2}i\delta t}\sin \left(\frac{1}{2}t\sqrt{{\delta }^{2}+4{{{{\rm{g}}}}}_{h}^{2}{\phi }_{h}^{2}}\right)}{\sqrt{{\delta }^{2}+4{{{{\rm{g}}}}}_{h}^{2}{\phi }_{h}^{2}}},$$
(10)
$$\delta ={\omega }_{0}+\nu -{\Omega }_{h}.$$

The work capacity (ergotropy) increase (gain) following the interaction in the cavity is (see “Ergotropy of the signal mode”)

$${{{\mathcal{W}}}}({\rho }_{s}^{f})-{{{\mathcal{W}}}}({\rho }_{s}^{i})=\nu (| v{| }^{2}-| u{| }^{2}),$$
(11)

which requires ∣v∣ > ∣u∣ and is maximized for ∣v∣ = 1, ∣u∣ = 0.

For the choice δ = 0, ght∣ϕh∣ = (2m + 1)π/2, where m is an integer, the atom is transferred to the excited state, and the signal add a photon to its mode, \({\rho }_{s}^{f}=\left\vert {n}_{s}+1\right\rangle \left\langle {n}_{s}+1\right\vert\). The highest amplification per atom is achieved for ns = 1. The efficiency of work extraction by the signal from the BH is then

$$\eta =\frac{\nu }{{\omega }_{0}+\nu }.$$
(12)

This efficiency can closely approach the Scovil-Schulz-Dubois (SSD) bound of quantum heat engine/amplifiers 22ν/(ω0 + ν). In turn, the SSD efficiency ηSSD can approach the Carnot efficiency ηC if \(\frac{{T}_{h}}{{T}_{c}}\gtrsim \frac{{\Omega }_{h}}{{\omega }_{c}}\). However, as Tc → 0, the atom resonant frequency must approach zero in order to attain the Carnot efficiency, which is unfeasible.

The maximal average output power in this regime is given by the time derivative of the ergotropy (work extraction) increase

$$\dot{{{{\mathcal{W}}}}}=\frac{2{g}_{h}| {\phi }_{h}| \nu }{(2m+1)\pi },$$
(13)

where the maximal power corresponds to m = 0.

A spectacular power boost can be obtained in the Dicke regime of N atoms that are collectively coupled to the hot bath mode. Following23, we can have

$$\dot{{{{\mathcal{W}}}}}\to N\dot{{{{\mathcal{W}}}}}.$$
(14)

Weak TLA-BH coupling

Let us now consider the opposite limiting regime of a cavity with insufficiently high Q and resonance frequency ωc ≈ ω0. Also, the detuning ∣ωc − Ωcj∣ of the cavity frequency from the cold-bath modes is small, so the atom equilibrates with the cold-bath modes ϕcj at TC = 0 and reaches its ground state \(\left\vert g\right\rangle\), following the interaction (6), which is now dominated by

$${H}_{{{{\rm{int}}}}}\approx \mathop{\sum}\limits_{j}\left({g}_{cj}{\phi }_{cj}{\hat{c}}_{cj}\vert e\rangle \langle g\vert +H.c.\right)$$
(15)

Though the atom reaches its steady state by the interaction with the cold-bath modes, the atom together with the signal mode are energized by the redirected Hawking radiations via coupling to the ϕhi modes (where ϕhi ≈ ω0 + ν). The process is analogous to our continuously operating heat-engine maser based on a TLA19. This treatment yields the effective Raman Hamiltonian for the atom-scalar-field coupling that reads (in the interaction picture)

$${H}_{{{{\rm{Raman}}}}}(t)={g}_{h}\mathop{\sum}\limits_{i}\left({\phi }_{hi}{\hat{a}}_{hi}{\hat{b}}^{{\dagger} }\vert e\rangle \langle g\vert {e}^{-i[{\Omega }_{hi}-(\nu +{\omega }_{0})]t}+H.c.\right).$$
(16)

Under this interaction, we get a master equation for the state of the hot scalar field (SN 2). By tracing out the atom, which has reached a steady state under the influence of the cold bath, we then find the time evolution of the signal mode19.

The ergotropy (work capacity) of the signal state, initially in a coherent state \(\left\vert {\alpha }_{0}\right\rangle\), undergoes coherent amplification as (SN 2)

$${{{\mathcal{W}}}}=\nu | {\alpha }_{0}{| }^{2}{e}^{{{{\mathcal{G}}}}t},$$
(17)

where ∣α0∣ is the mean initial signal amplitude and \({{{\mathcal{G}}}}\) is the gain19. The power of the gained work is, therefore, given by

$$\dot{{{{\mathcal{W}}}}}={{{\mathcal{G}}}}\nu | {\alpha }_{0}{| }^{2}{e}^{{{{\mathcal{G}}}}t}.$$
(18)

As in the strong-coupling regime, N-fold collective (Dicke) power boost23 is attainable by N atoms.

The efficiency can be computed as the ratio of the power generated by the signal to the heat flux from the BH, \({\dot{Q}}_{h}\), which is the rate of energy change of the working system induced by the heat bath effect12,24. In our scheme, \({\dot{Q}}_{h}=\,{{\mbox{Tr}}}\,({\dot{\rho }}_{h}{H}_{{{{\rm{TLA}}}}+{{{\rm{Signal}}}}})\), where \({H}_{{{{\rm{TLA}}}}+{{{\rm{Signal}}}}}={\omega }_{0}\left\vert e\right\rangle \left\langle e\right\vert +\nu {b}^{{\dagger} }b\) is the free (combined) Hamiltonian of the TLA and the signal mode. Given that Tc = 0, the efficiency then evaluates to (SN 2),

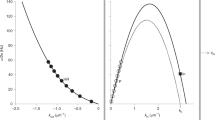
$$\eta =\frac{\dot{{{{\mathcal{W}}}}}}{{\dot{Q}}_{h}}=\frac{\nu }{{\Omega }_{h}}\frac{| {\alpha }_{0}{| }^{2}}{| {\alpha }_{0}{| }^{2}+1}.$$
(19)

This efficiency approaches the SSD bound ν/(ω0 + ν) as ∣α0∣>>1 (Fig. 2). In Fig. 3, we show that the division of the gained signal energy between increased ergotropy and generated heat tends in favor of ergotropy (coherent work production) as the gain increases.

Fig. 2: Efficiency bound: Efficiency η of the amplification process in terms of the initial mean squared amplitude of the signal ∣α0∣2.
figure 2

For large ∣α0∣2 the Scovil-Schulz-Dubois (SSD) limit is attained.

Full size image
Fig. 3: Amplification with time.
figure 3

Work capacity, ergotropy, thermal energy, and the mean energy of the signal field induced by the BH as a function of the amplifier gain \({{{\mathcal{G}}}}\) (in inverse time units).

Full size image

Discussion

We have put forth the possibility of black-hole (BH) gravity to act as the energizing source of coherent light amplification. The amplification is mediated by the Hawking radiation of the BH in the presence of an orbiting mirror that transforms outgoing Hawking radiation into ingoing Rindler quanta. It can be viewed as a BH-fueled heat engine that converts Hawking radiation into work in a coherent signal mode.

We stress that Hawking radiation produced by the BH plays a key role in the proposed effect, which can be clarified as follows. Assume that we block the Hawking radiation emanating from the BH event horizon before it hits the mirror. Then both the outgoing and the ingoing fields are in a Rindler vacuum state, unchanged by the orbiting mirror. In this case, the mirror does not generate photons, namely, there is no dynamical Casimir effect25, which would only occur by a mirror accelerated in the Minkowski vacuum, but not in the Rindler vacuum26. The free-falling atom can then only be excited upon allowing the Hawking radiation to be redirected back to the BH by the mirror, as we have shown.

The main energy source in our model is Hawking radiation, and not the kinetic or potential energy of the atoms. In principle, one can also use the kinetic energy of ground-state atoms passing through the cavity to amplify light27. Our results corroborate the view13,14,15,16 that, despite the unitarity of such processes, a BH can act as a heat source on falling matter28.

The amplifier power is proportional to the flux of Hawking radiation produced by the BH, which scales as 1/M229, whereas the Hawking (hot bath) temperature scales as 1/M. The efficiency is bounded by the Scovil-Schulz-Dubois limit22 but falls short of the Carnot bound, as explained after Eq. (12).

As the orbital distance of the mirror increases, the solid angle at which the BH spans the mirror decreases, and the efficiency is expected to likewise decrease, just as in the case of a solar cell whose efficiency depends on the solid angle subtended by the sun30. However, the decrease of the solid angle as one recedes from the source can be compensated by focusing: As the intensity is increased by focusing, so does the effective solid angle, since the energy flow density per solid angle remains unchanged. Hence, by tightening the focusing, one can make the solid angle of the source at the device equal to the solid angle of the radiation emitted by the device, so that the efficiency becomes independent of the distance. We note that the compensation of this effect by focusing is an idealization. In practice there will be limitations as to how much the focusing by an objective lens can be tightened to compensate for the loss of efficiency due to the decrease of the solid angle (or, equivalently, an increase of the mirror distance). The reason is that the angular aperture of an objective lens is limited by realistic values of the size of the lens and its focal length.

Concepts of quantum information theory and optics have been gaining prominence in the context of quantum effects of gravity31,32,33,34. We here venture in yet another direction, demonstrating that such effects may find practical use, such as propelling a spaceship by atoms falling into a BH. These results open a hitherto unexplored avenue that bridges quantum optics, quantum thermodynamics, and BH gravity.

Methods

Mode functions of photons resonant with free-falling atoms

Here, we consider a TLA with transition frequency ω freely falling into a non-rotating BH of mass M along a radial trajectory from infinity with zero initial velocity. We choose the gravitational radius rg = 2GM/c2 as a unit of distance and rg/c as a unit of time and introduce the dimensionless distance, time, and frequency as

$$r\to {r}_{g}r,\quad t\to ({r}_{g}/c)t,\quad \omega \to (c/{r}_{g})\omega .$$

In dimensionless Schwarzschild coordinates, the atom trajectory is described by the equations

$$\frac{dr}{d\tau }=-\frac{1}{\sqrt{r}},\quad \frac{dt}{d\tau }=\frac{r}{r-1},$$
(20)

where t is the dimensionless time in Schwarzschild coordinates, and τ is the dimensionless proper time for the atom. Integration of equations (20) yields

$$\tau =-\frac{2}{3}{r}^{3/2}+const,$$
(21)
$$t=-\frac{2}{3}{r}^{3/2}-2\sqrt{r}-\ln \left(\frac{\sqrt{r}-1}{\sqrt{r}+1}\right)+const.$$
(22)

For a scalar photon in the Regge-Wheeler coordinate

$${r}_{* }=r+\ln (r-1)$$
(23)

the field propagation equation reads

$$\left[\frac{{\partial }^{2}}{\partial {t}^{2}}-\frac{{\partial }^{2}}{\partial {r}_{* }^{2}}+\left(1-\frac{1}{r}\right)\left(\frac{1}{{r}^{3}}-\frac{{{\Delta }}}{{r}^{2}}\right)\right]\psi =0,$$
(24)

where Δ is the angular part of the Laplacian.

We are interested in solutions to this equation outside of the event horizon, that is, for r > 1. If the dimensionless photon frequency ν ≫ 1, then the first two terms in Eq. (24) dominate, and one can approximately write

$$\left(\frac{{\partial }^{2}}{\partial {t}^{2}}-\frac{{\partial }^{2}}{\partial {r}_{* }^{2}}\right)\psi =0.$$
(25)

The general solution of this equation reads

$$\psi =F\left(t\pm {r}_{* }\right)=F\left(t\pm r\pm \ln (r-1)\right),$$
(26)

where F is an arbitrary function.

We consider a trajectory of the atom near the event horizon and choose the origin of τ such that τ = 0 when the atom crosses the horizon. In the vicinity of the horizon, we obtain the atom’s trajectory

$$t\,\approx\, -\ln (-\tau )+\frac{5}{4}\tau +const,$$
(27)
$$r\,\approx\, 1-\tau -\frac{1}{4}{\tau }^{2},$$
(28)

and, therefore, along the atom’s trajectory

$$t-r-\ln (r-1)\,\approx\, -2\ln (-\tau )+const,$$
(29)
$$t+r+\ln (r-1)\,\approx\, \frac{1}{2}\tau +const.$$
(30)

Eqs. (29) and (30) yield the following mode functions of the field, which harmonically oscillates as a function of τ along the atom’s trajectory

$${\psi }_{1\nu }(t,r)={e}^{i\nu {e}^{-\frac{1}{2}\,\left(t-r-\ln (r-1)\right)}}\approx\, {e}^{-i\nu \tau },$$
(31)
$${\psi }_{2\nu }(t,r)={e}^{-2i\nu \left(t+r+\ln (r-1)\right)}\approx\, {e}^{-i\nu \tau }.$$
(32)

It is insightful to write the mode functions (31) and (32) in the Kruskal–Szekeres coordinates T and X that are defined in terms of the Schwarzschild coordinates t and r as

$$T=\sqrt{r-1}{e}^{\frac{r}{2}}\sinh \left(\frac{t}{2}\right),$$
(33)
$$X=\sqrt{r-1}{e}^{\frac{r}{2}}\cosh \left(\frac{t}{2}\right),$$
(34)

for r > 1, and

$$T=\sqrt{1-r}{e}^{\frac{r}{2}}\cosh \left(\frac{t}{2}\right),$$
(35)
$$X=\sqrt{1-r}{e}^{\frac{r}{2}}\sinh \left(\frac{t}{2}\right),$$
(36)

for 0 < r < 1. In these coordinates, we obtain for r > 1

$${e}^{-\frac{1}{2}\left(t-r-\ln (r-1)\right)}=X-T,$$
(37)
$$T+X={e}^{\frac{1}{2}\left(t+r+\ln (r-1)\right)},$$
(38)

and, therefore,

$${\psi }_{1\nu }(T,X)={e}^{-i\nu \left(T-X\right)},$$
(39)
$${\psi }_{2\nu }(T,X)={\left(T+X\right)}^{-4i\nu }.$$
(40)

Ergotropy of the signal mode

To estimate the work gain of the signal mode, we resort to ergotropy. The ergotropy of a quantum state ρ with a Hamiltonian H is defined as the maximal amount of average energy that can be extracted by means of a unitary transformation1. It reads

$${{{\mathcal{W}}}}(\rho ,H)=\,{{\mbox{Tr}}}\,(\rho H)-\mathop{\min }\limits_{U}\,\,{{\mbox{Tr}}}\,(U\rho {U}^{{\dagger} }H).$$
(41)

The part of the energy that cannot be extracted by a unitary transformation is the passive energy of the state. For a diagonal density matrix \(\rho =\sum {p}_{i}\left\vert {E}_{i}\right\rangle \left\langle {E}_{i}\right\vert\), the state is passive with respect to a Hamiltonian \(H=\sum {E}_{i}\left\vert {E}_{i}\right\rangle \left\langle {E}_{i}\right\vert\) only when

$${p}_{i}\ge {p}_{j},\,\,{{\mbox{if}}}\,\,{E}_{j}\, >\, {E}_{i}$$
(42)

Thus, the total mean energy of a quantum state can be considered as a sum of ergotropy and passive energy

$$E=\,{{\mbox{Tr}}}\,(\rho H)={E}_{{{{\rm{pas}}}}}+{{{\mathcal{W}}}}.$$
(43)

Let us assume that initially, the signal is at \(\left\vert {n}_{s}\right\rangle \left\langle {n}_{s}\right\vert\). By a unitary transformation \(\left\vert {n}_{s}\right\rangle \to \left\vert 0\right\rangle\), νns is the amount of energy that can be extracted from the state. Correspondingly, the initial ergotropy of the piston mode is given by

$${{{\mathcal{W}}}}[{\rho }_{s}^{i}]=\nu {n}_{s}.$$
(44)

From the final state of the signal mode (Eq. (9)) maximal work extraction is achieved by a unitary transformation: \(\{\left\vert {n}_{s}+1\right\rangle \to \left\vert 0\right\rangle ;\left\vert {n}_{s}\right\rangle \to \left\vert 1\right\rangle \}\) (when ∣v∣2 > ∣u∣2). Therefore, the final ergotropy of the signal mode is

$${{{\mathcal{W}}}}[{\rho }_{s}^{f}]=\nu [{n}_{s}+(| v{| }^{2}-| u{| }^{2})].$$
(45)

The ergotropy (or the work) gain is then

$${{{{\mathcal{W}}}}}_{{{{\rm{gain}}}}}=\nu (| v{| }^{2}-| u{| }^{2}),$$
(46)

which is maximized when ∣v∣2 = 1.