Introduction

Single-photon sources with high purity, indistinguishability, and efficiency are critical components in the rapidly advancing field of quantum technologies1. While various methods have been explored, one of the most important approaches to generating single photons is through quantum emitters: two-level quantum systems with the ability to emit one photon at a time. In contrast to stochastic nonlinear processes such as atomic cascade2, parametric down-conversion3, and four-wave mixing4, quantum emitters provide a deterministic and scalable source of single photons. Many promising systems have been identified for realizing ideal single-photon emitters, including single atoms5, single ions6, single molecules7, color centers8, and semiconductor quantum dots (QDs)9. Intriguingly, microscopic defects10,11,12,13,14 and moiré-trapped excitons15,16 in two-dimensional materials and perovskite colloidal QDs17,18,19,20 have also been demonstrated to emit single photons. Of particular note, several of these systems exhibit on-demand single-photon emission with high efficiency, scalability, and compatibility with on-chip integration21. As such, they hold significant promise for developing practical applications in quantum communication, sensing, and computing.

Despite the significant potential of semiconductor QDs as quantum emitters, their large spectral linewidth due to the pure dephasing processes, compared with the nonlinear processes and the natural broadening of the emitter itself, poses a major challenge, which can severely diminish the single-photon indistinguishability22,23. The broadening of the linewidth is typically caused by random energy fluctuations resulting from spectral diffusion24,25,26 as well as phonon scattering23,27,28,29. Spectral diffusion occurs due to the time-fluctuating quantum confined Stark effect resulting from the interaction between the QDs and charged defects in the electrostatic environment30,31. This interaction significantly reduces the indistinguishability of the single-photon emission. Although spectral diffusion can be partially suppressed by applying sequences of optical pulses32, strong illumination33, exploiting the Purcell effect induced by a photonic cavity34, or a Fano cavity-photon interface35, all of these methods require external controls, which can constrain scalability and have limited efficiency in suppressing spectral diffusion. Phonon scattering, which results from exciton-acoustic phonon coupling, accounts for the homogeneous broadening of single-photon emission and is greatly affected by the temperature36,37. This effect becomes increasingly pronounced at higher temperatures38,39, which poses a significant obstacle for single-photon emission at room temperature. Some works are also trying to reduce the influence of the phonon interaction40.

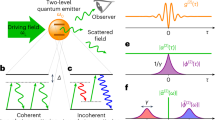
In photonic systems, introducing non-trivial topology is an intriguing approach to achieving intrinsic robustness41,42. However, most of the existing topological systems operate in the classical or semi-classical regime43, where the quantum nature of photons is not a significant factor. For instance, topological insulators have been used for robust lasing in edge modes that extend over multiple lattice sites along the boundaries of the system44,45,46. The robustness in lasing comes from the global topology of the edge modes, which enables them to bypass local defects and deformations through nearby alternative paths, thereby maintaining the global topology. However, such methods are not suitable for the zero-dimensional geometry of quantum emitters like QDs. Although strong optical nonlinearity can be utilized for single-photon generation, it is typically local in nature, and thus, extended edge states of topological insulators would be incompatible47,48. Furthermore, topological structures are usually used as passive platforms for quantum information transportation49,50,51,52. However, active quantum systems like single-photon emitters must also be robust to realize an infallible quantum platform ultimately. This study explores the possibility of using the Su-Schrieffer-Heeger (SSH) topology in active quantum systems to generate robust single photons. Since the emission must be localized at a single site and not from an entire edge state, it is counter-intuitive to expect topological robustness. Nonetheless, we discovered that the single-photon emission exhibits dramatic robustness to noise near the topological non-trivial-to-trivial phase transition point where the spectrum becomes arbitrarily narrow for large system sizes. This provides highly indistinguishable single photons even in a strongly noisy environment. We present the microscopic mechanism and explore physical systems for experimental realization.

Results

The model

A collection of N quantum emitters (represented by QDs), organized in an SSH chain53,54,55, constitutes an active quantum system that can be described by a Hamiltonian H (see Supplementary Note 3 for details):

$${\mathcal{H}}\,=\,\mathop{\sum }\limits_{j}{{\rm{\varepsilon }}}_{j}\left(t\right){{\rm{\sigma }}}_{j}^{+}{\sigma }_{j}^{-}+\mathop{\sum }\limits_{j}{J}_{j}({\sigma }_{j}^{+}{\sigma }_{j+1}^{-}+{\sigma }_{j+1}^{+}{\sigma }_{j}^{-}),$$
(1)

where \({{\rm{\sigma }}}_{j}^{+}\) (\({{\rm{\sigma }}}_{j}^{-}\)) is the creation (annihilation) operator associated with the QD emitter at the site j. The Hamiltonian is written in an interacting frame of reference, where the central energy is shifted to zero. Our idea is to excite the entire chain and collect the emission from the edge QD. Here, the QD is defined as a two-level quantum system that can emit one photon at a time. The chain consists of N/2 unit cells, each containing two sites. The hopping amplitude Jj = J for odd j (intra-cell) and Jj = J′ for even j (inter-cell). The onsite energy εj (t) represents microscopic energy fluctuations: \({{\rm{\varepsilon }}}_{j}\left(t\right)={\rm{\epsilon }}{\rm{\delta }}{{\rm{\varepsilon }}}_{j}\left(t\right)\), where \({\rm{\delta }}{{\rm{\varepsilon }}}_{j}\left(t\right)\) is a Gaussian random variable and ϵ is the noise strength. The noise could originate from spectral diffusion and phonon scattering. In the ideal condition, the SSH chain with the onsite energy \({{\rm{\varepsilon }}}_{j}\left(t\right)=0\) (or a constant value) has a winding number:

$$W=\frac{1}{2{\rm{\pi }}i}{\int }_{-{\rm{\pi }}}^{{\rm{\pi }}}{dk}\frac{d}{{dk}}\log \left[h\left(k\right)\right],$$
(2)

where \(h\left(k\right)=J+{J}^{{\prime} }{e}^{{ik}}\). We parameterize \(J={J}_{0}{\sin }^{2}{\rm{\theta }}\) and \({J}^{{\prime} }={J}_{0}{\cos }^{2}{\rm{\theta }}\), where J0 is a constant and θ is an angular parameter ranging in \(\left[0,{\rm{\pi }}/2\right]\). For \({{\theta }} \,<\, {{\pi }}/4\), the chain has a non-trivial topology with a winding number W = 1. Our idea is to obtain single photons from the topological edge states (see Fig. 1), which are energetically located inside a band gap.

Fig. 1: Three schemes of generating single photons: single QD, topologically trivial, and non-trivial chains of QDs.
figure 1

The emission spectrum of the topologically non-trivial chain is much narrower than that of the trivial chain, which in turn is broader than that of a single QD. The inset shows the eigenvalues of the SSH Hamiltonian as a function of the parameter \(\theta =\arctan \left(\sqrt{J/{J}^{{\prime} }}\right)\), where J and J' are the intra-cell and inter-cell hopping amplitude. The topological non-trivial-to-trivial phase transition occurs at \({\rm{\theta }}={\rm{\pi }}/4\).

Full size image

Here, we focus on the spontaneous emission spectrum, which is related to the time-dependent many-body correlation function:

$${C}_{j}\left(t,{t}^{{\prime} }\right)=\left\langle {{\rm{\sigma }}}_{j}^{+}\left(t\right){{\rm{\sigma }}}_{j}^{-}\left({t}^{{\prime} }\right)\right\rangle ,$$
(3)

where \(\langle {\mathscr{O}}\rangle\) indicates the expectation value of an operator \({\mathscr{O}}\). Our objective is to determine the emission characteristics of the system with non-trivial topology. To achieve this, we assume that the system is initially in an excited state at time t = 0, and we use an ideal detector to capture emissions from an edge site. The detector records photons for an indefinite duration. The corresponding single-photon spectrum is given by56

$${S}_{j}(\omega )=\frac{{\int }_{0}^{\infty }dt{\int }_{0}^{\infty }dt^{\prime} {C}_{j}(t,t^{\prime} ){e}^{-i\omega (t-t^{\prime} )}}{2\pi {\int }_{0}^{\infty }dt{C}_{j}(t,t)}.$$
(4)

As an example, the spectral profile of an ideal emitter possessing a long lifetime is described by \({\rm{\delta }}(\hslash {\rm{\omega }}-{\rm{\varepsilon }})\), where the emitted photons are indistinguishable with a fixed energy \(\hslash {\rm{\omega }}={\rm{\varepsilon }}\). It is worth mentioning that the lifetime of a quantum emitter typically ranges in the order of nanoseconds, resulting in a negligibly narrower linewidth compared to the actual linewidth; see Supplementary Discussion and Supplementary Table 1 for further details.

Emission spectra

The spectral profile of an isolated emitter can be determined through the use of the retarded Green’s function: \({{S}_{1}\left({\rm{\omega }}\right)=-{\rm{Im}}\left[{G}^{R}\left({\rm{\omega }}\right)\right]}\). In the case of an ideal emitter, the Green’s function can be expressed as \({G}^{R}\left({{\omega }}\right)={li}{m}_{{{\eta }}\to 0}{\left({{\omega }}{{\hslash }}+i{{\eta }}\right)}^{-1}\) indicating a single energy emission at \({\rm{\hslash }}{\rm{\omega }}=0\). In the presence of noise, the system can be characterized by an averaged Green’s function: \({\bar{G}}^{R}\left({{\omega }}\right)={\mathop{\mathrm{lim}}\nolimits_{{{\eta }}\to 0}\left[{{\omega }}{{\hslash }}+i{{\eta }}-\Sigma \right]}^{-1}\) where Σ is the self-energy of the emitter57. As a result, the corresponding spontaneous emission spectrum is given by

$${S}_{1}\left({{\omega }}\right)=\frac{1}{{{\pi }}}\frac{-{\rm{Im}}\Sigma }{{\left({{\hslash}}{{\omega }}\right)}^{2}+{\left({{Im}}\Sigma \right)}^{2}},$$
(5)

which follows a Lorentzian distribution featuring a linewidth (full width at half maximum): \(-2{\rm{Im}}\Sigma ={{\rm{\gamma }}}_{\text{QD}}+{{\rm{\gamma }}}_{0}\), where \({{\rm{\gamma }}}_{\text{QD}}\) and \({{\rm{\gamma }}}_{0}\) are the linewidth contributions from the noise and recitative lifetime of the QD. Typically, spectral linewidth \(-2{\rm{Im}}\Sigma \gg {{\rm{\gamma }}}_{0}\) (see Supplementary Table 1) implying \({{\rm{\gamma }}}_{\text{QD}}\gg {{\rm{\gamma }}}_{0}\). The linewidth \({{\rm{\gamma }}}_{\text{QD}}\) is determined by the noise correlation function: \(\overline{{\rm{\delta }}{{\rm{\varepsilon }}}_{j}\left(t\right){\rm{\delta }}{{\rm{\varepsilon }}}_{j}\left({t}^{{\prime} }\right)}={{\rm{\epsilon }}}^{2}{e}^{-{\left(t-{t}^{{\prime} }\right)}^{2}/\left(2{{\rm{\tau }}}^{2}\right)}\), where the overline represents the noise average and τ is the correlation time. In the lowest order Dyson series, \(\Sigma \approx -\left(i{{{\epsilon }}}^{2}{{\tau }}\sqrt{{{\pi }}}\right)/\left({{\hslash }}\sqrt{2}\right)\)57. We note that while the exact numerical value \({{\rm{\gamma }}}_{\text{QD}}=\) 0.400 meV (see Fig. 2), the analytical values are 0.470 meV and 0.403 meV with the lowest order approximation and a self-consistent method, respectively (see Supplementary Note 1 and 2 for details). This non-zero linewidth indicates the presence of spectral diffusion, whereby emitted photons possess slightly varying energy with each emission.

Fig. 2: Topological linewidth narrowing.
figure 2

a The single-photon spectrum \({S}_{1}\left({\rm{\omega }}\right)\) for a topological SSH chain (\({\rm{\theta }}={\rm{\pi }}/4.2\)) of size N. The points and lines are the data and corresponding Lorentzian fits, respectively. The inset shows the spectral linewidth γSSH as a function of N at \({\rm{\theta }}={\rm{\pi }}/4.2\). For an isolated QD (N = 1), we numerically find that the linewidth \({{\rm{\gamma }}}_{\text{QD}}\approx 0.4\) meV. b The variation of γSSH (normalized by γQD) with θ for N = 80 (blue squares) and 200 (red dots). The linewidth dramatically decreases near \({\rm{\theta }}={\rm{\pi }}/4\). As the horizontal dotted lines indicate, the value \({{\rm{\gamma }}}_{\text{SSH}}\) (\({\rm{\theta }}\to {\rm{\pi }}/4\)) becomes smaller for a larger N. The inset shows that \({{\rm{\gamma }}}_{\text{SSH}}\) (\({\rm{\theta }}\to {\rm{\pi }}/4\)) becomes systematically smaller with the increasing N. c The ratio between γSSH and the band gap Δ as a function of the hopping amplitude J0. We consider \({\rm{\epsilon }}=0.5\) meV, \({\rm{\tau }}=0.5\) ps, \({\rm{\theta }}={\rm{\pi }}/4.2\), and \({J}_{0}=30\) meV when they are not used as variables. For simulation, we use a topological edge mode as the initial state and 10 noise realizations for average.

Full size image

Topological linewidth narrowing

We present in Fig. 2 the linewidth narrowing of single-photon emission via coupling QDs in a topologically non-trivial SSH chain. We consider that the system is initially excited to the topological edge state, extending over many sites in the SSH chain. Since the edge state is energetically separated from all the other states by the topological band gap, the initial state can be excited by a resonant pulse. Subsequently, the emission occurs at the edge site (j=1) of the SSH chain, and we depict the emission spectrum for various chain sizes. Notably, as the length of the chain N increases, the linewidth (full width at half maximum) γSSH significantly diminishes, as shown in Fig. 2a. This finding suggests that the topological non-triviality profoundly impacts mitigating the detrimental effects of noise on the edge QD. However, we observe that this effect is feeble for \(J/{J}^{{\prime} }\ll 1\) (\({\rm{\theta }}\ll {\rm{\pi }}/4\)) despite being in the topological non-trivial regime. This can be traced back to the weak coupling between the edge QD and the remaining SSH chain for \(J\ll {J}^{{\prime} }\), rendering the edge QD nearly isolated. It is only near the phase transition point \({\rm{\theta }}={\rm{\pi }}/4\) where \(J/{J}^{{\prime} }\approx 1\) that the effect of the global topology becomes noticeable in the chain, as shown in Fig. 2b, where the linewidth γSSH displays a significant decrease near \({\rm{\theta }}={\rm{\pi }}/4\). Of particular importance, the linewidth narrowing is further enhanced with increasing system size N, and in fact, can even be made arbitrarily stronger for large N and θ close to \({\rm{\pi }}/4\) (see Fig. 2b). Nevertheless, the topological robustness of the system is guaranteed only if the linewidth is much smaller than the band gap Δ, i.e., \({{\rm{\gamma }}}_{\text{SSH}}/\Delta\) is close to 0. Since the band gap Δ is directly proportional to the hopping amplitude J0, a large J0 is also necessary to achieve this regime, as demonstrated in Fig. 2c. Asymptotically, the limit of an arbitrarily small linewidth \({{\rm{\gamma }}}_{\text{SSH}}\to 0\) while having a finite topological band gap is reached with N → ∞, J0 →, and θ → π/4.

We note that the phenomenon of linewidth narrowing is absent in a topologically trivial chain. In a trivial chain, QDs within the lattice act as sources of additional noise for the single-photon emission, which, in fact, leads to a broadening of the linewidth (see Supplementary Note 6 and Supplementary Fig. 6). This is primarily due to the lack of a topological energy band gap near the emitting state.

In addition to time-fluctuating noise, static disorders may also arise due to defects and imperfections in the system. First, each individual QD may have a different emission energy, representing static randomness in the energy. We observe that SSH chains composed of such disordered QDs suppress spectral randomness. Besides, while forming the SSH chain, the positions of the QDs might not be precise. These imperfections would introduce randomness in the hopping strengths J and J′. Despite the presence of these disorders, the SSH topological chain still exhibits a significant linewidth narrowing effect (see Supplementary Note 7 and Supplementary Fig. 8).

Statistical properties of the Hamiltonian

Statistical properties of the Hamiltonian allow us to understand the topological linewidth narrowing. We examine the eigenvalue distribution of the Hamiltonian with a randomly chosen noise potential at an instant of time, which is given by the density of states of an effective single-particle Hamiltonian matrix \({H}_{{jk}}={{\rm{\varepsilon }}}_{j}{{\rm{\delta }}}_{j,k}-{J}_{j}{{\rm{\delta }}}_{j+1,k}\). Note that simulating a large number of emitters is challenging due to the exponentially large Hilbert space. Using the Jordan-Wigner transformation, the present problem of the bosonic (photonic) emitters can be mathematically converted to a free Fermionic problem (see Supplementary Note 5 for details), which is computationally tractable58. Figure 3a shows the density of states \({D}_{s}\left(E\right)=\overline{\text{Tr}\left[{\rm{\delta }}\left(H-E\right)\right]}\) as a function of energy E and θ. The existence of a finite density of states around E=0 and a band gap for \({{\theta }} \,<\, {{\pi }}/4\) evidence the topological non-triviality, whereas the region \({{\theta }} \,>\, {{\pi }}/4\) is topologically trivial. Interestingly, we find that the density of states near the energy E=0 becomes narrower as θ is close to \({\rm{\pi }}/4\), suggesting that the energy distribution of the edge states is highly constrained, which propels the spectrum to be narrow. A more thorough examination of the eigenvalues associated with the edge states of the Hamiltonian H, as illustrated in Fig. 3b–e, unveils a significant reduction in eigenvalue fluctuations near the transition point \({\rm{\theta }}={\rm{\pi }}/4\). This compelling evidence of topological robustness serves as the driving force behind the linewidth narrowing observed in Fig. 2.

Fig. 3: Statistical properties of the SSH Hamiltonian.
figure 3

a Color plot of the averaged density of states \({D}_{s}\left(E\right)=\overline{\text{Tr}\left[{\rm{\delta }}\left(H-E\right)\right]}\) for different θ. b Eigenvalues associated with edge states as functions of θ for different noise realizations (edge states exist for \({{\theta }} \,<\, {{\pi }}/4\)). All eigenvalues collapse towards E = 0 near \({{\theta }}={\rm{\pi }}/4\) due to dramatic suppression of fluctuations close to the phase transition point. This is the underlying reason for topological linewidth narrowing. c–e Probability distributions of edge state eigenvalues for θ = 0, 0.2π, and 0.23π, respectively. We find that the distribution becomes narrower as θ approaches \({\rm{\pi }}/4\). Here we consider \({J}_{0}=5\) meV and \({\rm{\epsilon }}=0.5\) meV.

Full size image

Quantum correlation properties

To confirm our system works at the single-photon level, we simulate the Hanbury Brown and Twiss (HBT) effect59 and the Hong-Ou-Mandel (HOM) effect60, which reflect the single-photon purity and indistinguishability of the single-photon emission. To excite the topological edge state at ω = 0, we consider a resonant excitation scheme with the Hamiltonian:

$${{\mathcal{H}}}_{P}={\mathcal{H}}+P(t)\sum _{j}({\sigma }_{j}^{+}+{\sigma }_{j}^{-}),$$
(6)

where P(t) represents the excitation applied to all QDs in the SSH chain. The dynamics of the system can be described by the quantum master equation:

$$i{{\hslash }}\dot{\rho }=\left[{{\mathcal{H}}}_{P},\rho \right]+\frac{i{{{\gamma }}}_{0}}{2}\mathop{\sum }\limits_{j}\left(2{{{\sigma }}}_{j}^{-}\rho {{{\sigma }}}_{j}^{+}-{{{\sigma }}}_{j}^{+}{{{\sigma }}}_{j}^{-}\rho -\rho {{{\sigma }}}_{j}^{+}{{{\sigma }}}_{j}^{-}\right),$$
(7)

where γ0 represents the decay rate of the QDs. Crucially, due to the presence of excitation and the Lindblad term in Eq. (7), utilizing the Jordan-Wigner transformation does not confer any advantages. Therefore, our calculations are confined to a relatively small number of QD (up to 12) in the chain. Nevertheless, even within this constrained number of QD, we observe topological robustness in the single photon properties.

First, we calculate the second-order correlation function between emissions at two-time instances, denoted as t and t′ under a continuous-wave (CW) pump (\(P\left(t\right)={P}_{0}\)). The second-order correlation function for QD located at lattice site j is expressed as follows:

$${g}_{j}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)=\frac{\left\langle {{\rm{\sigma }}}_{j}^{+}\left(t\right){{\rm{\sigma }}}_{j}^{+}\left({t}^{{\prime} }\right){{\rm{\sigma }}}_{j}^{-}\left(t\right){{\rm{\sigma }}}_{j}^{-}\left({t}^{{\prime} }\right)\right\rangle }{\left\langle {n}_{j}\left(t\right)\right\rangle \left\langle {n}_{j}\left({t}^{{\prime} }\right)\right\rangle },$$
(8)

where \({n}_{j}\left(t\right)={{\rm{\sigma }}}_{j}^{+}\left(t\right){{\rm{\sigma }}}_{j}^{-}\left(t\right)\). Figure 4a, b depict the second-order correlation function \({g}_{1}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)\) as a function of the time delay t-t′ in the steady state for a single QD and the edge QD of a topological SSH chain, respectively. We demonstrate the edge QD in a chain preserves the single-photon purity compared with the single QD and the robustness against noise. In contrast, topologically trivial chains show strong oscillations around zero time delay in the second-order correlation function, which is unsuitable for single-photon emission (see Supplementary Fig. 7).

Fig. 4: Quantum correlation properties.
figure 4

a Second-order correlation function \({g}_{1}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)\) as a function of the time delay t - t′ for a single QD without (dotted line) and with (black solid line with points) noise. b \({g}_{1}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)\) for topological SSH chain without (dotted line) and with (red solid line with dots) noise. As can be seen, \({g}_{1}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)\) is almost unaffected by noise. Here we consider, \({J}_{0}=30\) meV, \({\rm{\theta }}={\rm{\pi }}/5\), noise strength \({\rm{\epsilon }}=0.5\) meV, CW excitation strength \({P}_{0}=0.5\) meV, and decay strength \({{\rm{\gamma }}}_{0}=1\) meV. c The HOM visibility as a function of hopping amplitude J0. The visibility for a single QD is \({V}_{1}=0.958\). For the SSH chain, we consider QD numbers N = 4, 6, 8, and 12. When J0 is relatively large, V1 is increased with a larger N. Here, we set the excitation strength P0 = 3 meV, period 2T = 5 ps, and time interval Δt = 0.15 ps. All the results are averaged over 64 noise realizations.

Full size image

Next, we calculate the indistinguishability of the single-photon emission represented by the HOM visibility61. Here, we consider a pulsed excitation with the form \(P\left(t\right)={P}_{0}{\sum }_{n}\exp [-{\left(t-2{nT}\right)}^{2}/\left(2\Delta {t}^{2}\right)]\), where 2T is the period that the system is excited and Δt is the time interval. We define the intensity cross-correlation function for the HOM measurement as

$${G}_{j}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)=\frac{1}{2}\left[\left\langle {n}_{j}\left(t\right)\right\rangle \left\langle {n}_{j}\left({t}^{{\prime} }\right)\right\rangle +\left\langle {{\rm{\sigma }}}_{j}^{+}\left(t\right){{\rm{\sigma }}}_{j}^{+}\left({t}^{{\prime} }\right){{\rm{\sigma }}}_{j}^{-}\left(t\right){{\rm{\sigma }}}_{j}^{-}\left({t}^{{\prime} }\right)\right\rangle -{\left|\left\langle {{\rm{\sigma }}}_{j}^{+}\left(t\right){{\rm{\sigma }}}_{j}^{-}\left({t}^{{\prime} }\right)\right\rangle \right|}^{2}\right].$$
(9)

Since \({G}_{j}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)\) goes to 0 around zero delay time, the single-photon indistinguishability for a lattice site j is evaluated by the HOM visibility Vj:

$${V}_{j}=1-\frac{{\int }_{0}^{T}{dt}{\int }_{T}^{-T}d{t}^{{\prime} }{G}_{j}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)}{{\int }_{0}^{T}{dt}{\int }_{3T}^{T}d{t}^{{\prime} }{G}_{j}^{\left(2\right)}\left(t,{t}^{{\prime} }\right)},$$
(10)

The results of the edge QD (j = 1) V1 are shown in Fig. 4c. With our considered parameters, the HOM visibility \({V}_{1}=0.958\) for a single QD. Intriguingly, we can see that the HOM visibility for a topological SSH chain is larger than that of a single QD. Besides, the visibility is improved when there are more QDs close to the topological phase transition point (\({\rm{\theta }}\to {\rm{\pi }}/4\)), which is consistent with the topological linewidth narrowing shown in Fig. 2. These results demonstrate that the indistinguishability of the emission at the single-photon level can be systematically improved by increasing the SSH chain size.

Micropillars

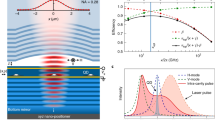
Micropillars62 offer a promising platform to realize our proposed scheme for achieving topological linewidth narrowing. Since strong quantum hopping (J and J′) is a requirement, we must estimate the hopping strength for micropillar systems. This system can be described by an effective Hamiltonian \({{\mathcal{H}}}_{{\rm{sys}}}=-\left({{{\hslash }}}^{2}{\nabla }^{2}\right)/\left(2{m}_{\text{eff}}\right)+V\left(r\right)\), where the effective mass meff is a material parameter and the potential energy V(r) represents the micropillars. As schematically depicted in Fig. 5a, a potential well with a certain depth represents a micropillar with a certain height. We investigate the dependence of the hopping amplitude Jsys between two micropillars on parameters such as effective mass, potential well depth, and distance between the micropillars. Our simulations consider parameters for different materials, such as GaAs QDs, defects (can be regarded as QDs) in WSe2 monolayer, and colloidal CsPbBr3 QDs.

Fig. 5: Estimation of the hopping amplitude for different materials.
figure 5

a The effective potential energy configuration of two micropillars separated by a distance. b Hopping amplitude Jsys as a function of the energy depth of the micropillars for different materials (GaAs, WSe2, and CsPbBr3). c Jsys as a function of the distance between two micropillars. d Jsys as a function of the effective mass of the micropillar quantum dots. The parameter γQD is the linewidth of QDs in respective materials. We consider \({m}_{\text{eff}}=0.05{m}_{e}\), depth 10 meV and distance 5 nm, when they are not variables. The single QD linewidth γQD = 0.15, 0.18, and 1 meV for GaAs, WSe2, and CsPbBr3, respectively.

Full size image

As shown in Fig. 5b, our analysis reveals that Jsys decreases as the depth of the potential well increases (see Supplementary Note 4 for further analysis). Additionally, smaller distances between micropillars and smaller effective masses lead to larger Jsys, as demonstrated in Fig. 5c, d. Notably, different materials exhibit different single-photon broadening, necessitating a comparison of Jsys with the linewidth γQD. We find that \({J}_{\text{sys}}/{{\rm{\gamma }}}_{\text{QD}}\) can reach values as high as 50, 40, and 5 for GaAs, WSe2, and CsPbBr3, respectively. Thus, our investigation suggests that the realization of our proposed scheme of topological linewidth narrowing is feasible with available materials.

Coupling with microcavities

We have determined that the effective mass meff plays a crucial role in controlling Jsys. However, it is impossible to directly change meff for a given material. To address this issue, we leverage the concept of light-matter coupling in a microcavity system to manipulate the effective mass. In such a system, the micropillar-QD systems are positioned inside microcavities such that the excitons in QDs can be coherently coupled to the cavity photons, which can be understood using the exciton-polariton picture63,64,65,66. The corresponding Hamiltonian is given by

$${{\mathcal{H}}}_{{\rm{tot}}}=\left(\begin{array}{cc}{{\mathcal{H}}}_{{\rm{sys}}} & \delta \\ \delta & -{({{\hslash }}\nabla )}^{2}/(2{m}_{c})\end{array}\right),$$
(11)

where mc is the effective mass of the cavity photons (\({m}_{c}\ll {m}_{\text{eff}}\)), and δ determines the coupling strength between cavity photons and QDs. As QDs coherently couple to the cavity, an additional channel for the hopping process is created, leading to a reduction in the effective mass. This results in an enhancement of Jsys, as demonstrated in Fig. 6.

Fig. 6: Enhancing the hopping amplitude by light-matter coupling.
figure 6

a A schematic representation of the coupling between the micropillar-QD system and microcavity. b Jsys as a function of the coupling strength δ between QDs and the optical cavity for GaAs, WSe2, and CsPbBr3, respectively. Here, \({m}_{\text{eff}}=0.05{m}_{e}\), depth is 10 meV, and \({m}_{c}={10}^{-4}{m}_{e}\).

Full size image

Discussion

Our approach for achieving topological linewidth narrowing holds great promise for extending to any two-level quantum emitters, including trapped atoms, ions, or superconducting qubits. Emissions stemming from certain electronic transitions in trapped atoms and ions can be harnessed for single-photon generation67,68. Moreover, they offer advanced techniques for precisely controlling the positions of individual atoms or ions. Therefore, implementing the SSH chains in these systems is certainly achievable using state-of-art technologies. Superconducting qubits provide another platform for implementing SSH chains of two-level quantum systems. In this setup, microwave photons can be detected to investigate the narrowing of the spectral linewidth69. Furthermore, our scheme could also be used to enhance the operating temperature of quantum emitters since topological linewidth narrowing in quantum SSH chains can effectively compensate for thermal broadening at high temperatures. In fact, by increasing the size of the SSH chain (N approaches ∞), the noise-induced linewidth can be arbitrarily reduced (γSSH approaches to 0), which in principle could enable enhancement of the operating temperature to a high value. Another essential concept in the field of quantum optics is the super/subradiance, which represents the phenomenon that enhances/suppresses the emission due to constructive/destructive interference between the emitters70. The coupled QD system has shown the ability to achieve and control the two states71,72,73, so it can also be applied in our SSH system, though detailed discussion on this topic is beyond our scope in this work.

We note that a nonzero linewidth appears from the finite lifetime of a QD. However, such a contribution in our considered system is extremely small compared to the actual linewidth (see Supplementary Table 1). Typically, spectral linewidth corresponding to the finite lifetime is several orders smaller than the actual linewidth (γQD). Thus, while such a small effect is inconsequential in our present work, it does put an asymptotic limit to the topological linewidth narrowing. However, note that narrowing the linewidth beyond this limit would also decrease the emission rate, and thus, it might be detrimental to the overall performance. For real applications, we may make a compromise between the emission rate and the emission linewidth to avoid an emission rate that is too low. A narrow linewidth can also pose a challenge for exciting the system. For controllable systems, such as trapped atoms and ions, one may drive the system into the topologically trivial phase (characterized by a large linewidth) for excitation and then return the system to the topological phase to achieve single-photon emission.

In practice, experimental challenges exist in achieving single-photon emission from fabricated QDs with high reproducibility. Nevertheless, significant progress has been made in fabricating single-photon emitters with specified site information. Strategies include pre-patterning the semiconductor substrate before epitaxy and subsequent guiding of the nucleation of III-V quantum dots74,75 or chemically assisted assembly of colloidal perovskite nanocrystals76,77. In addition, pillar sites defined with optimized lithography procedure have been shown to give rise to local strain for 2D semiconductors with a high yield of single-photon emission78,79. More recently, the implementation of SSH Hamiltonian and the presence of edge states has been experimentally demonstrated utilizing phosphorus donors in silicon quantum dot arrays where the electrons are strongly interacting80. Therefore, we hope our scheme will be considered a viable method to realize robust single-photon emitters. Another remaining challenge is selectively channeling emitted photons from the edge site (j = 1) to the detector. This could be addressed by coupling a waveguide structure between the edge site and the detector or by some kinds of spatial filters81,82.

In conclusion, we have devised a scheme for reducing linewidth in single-photon emission by arranging quantum emitters in a topologically non-trivial SSH lattice. We observe that near the topological phase transition point, the linewidth experiences a drastic reduction, becoming much smaller than that of an isolated emitter. For a large system size, the linewidth can be made arbitrarily small near the transition point, but a sufficiently strong hopping amplitude is necessary to maintain a substantial band gap. We show that the linewidth narrowing is intimately linked to the suppression of eigenvalue fluctuations in the vicinity of the transition point. We also identify several physical systems that offer promising prospects for the experimental realization of our scheme. Our approach is conducive to being integrated into quantum information processing devices based on photonic chips. It is inherently scalable, thereby facilitating its ultimate application to a vast number of quantum emitters on photonic platforms without requiring external control.