Introduction

As the field of quantum computing and quantum information gains traction, more manufacturers are entering the market, developing their own quantum computers. However, the current generation of noisy intermediate-scale quantum (NISQ) computers, despite their potential, is still hindered by quantum noise1. A great challenge is how to compare the performance of the quantum computers fabricated by different manufacturers and located in different laboratories, termed as cross-platform comparison. This task is especially relevant when we move towards regimes where comparing to classical simulations becomes computationally challenging, and therefore a direct comparison of quantum computers is necessary.

A standard method to achieve cross-platform comparison is quantum tomography2, in which we first reconstruct the full information of quantum computers under investigation and then estimate their fidelity from the obtained matrices. However, quantum tomography is known to be time-consuming and computationally difficult; even learning a few-qubit quantum state poses experimental challenges3,4. A more efficient way is to compare quantum computers directly without resorting to the full information. Indeed, a variety of certification and benchmarking tools5,6, such as fidelity estimation7,8,9,10,11,12, quantum verification13,14,15,16, and quantum benchmarking17,18,19,20,21, have been developed along this way. However, these methods commonly assume that one can access a known and theoretical target usually simulated by classical computers. They quickly become inaccessible for quantum computers containing several hundreds or even thousands of highly entangled qubits, due to the exponentially increasing time complexity in simulating classical computers. Therefore, there is a pressing need for directly comparing unknown quantum states and processes across distinct devices situated at various locations and temporal instances22.

Recently, Elben et al.23 proposed the first cross-platform protocol for estimating the fidelity of quantum states, possibly generated by spatially and temporally separated quantum computers. This protocol requires only local measurements in randomized product bases and classical communication between quantum computers. Numerical simulation shows that its sample complexity scales exponentially as \({\mathcal{O}}({2}^{bn})\) with b ≲ 1, where n is the number of qubit. This is significantly less than full quantum state tomography which has an exponent b ≥ 2. It is applicable in state-of-the-art quantum computers consisting of a few tens of qubits24. Later on, Knörzer et al.25 extended Elben’s proposal to cross-platform comparison of quantum networks, achieving a linear scaling of sample complexity at the cost of requiring quantum links. Nevertheless, a quantum link transferring quantum states of many qubits with high accuracy between two distant quantum computers is far from reach in the near future.

In this work, by elaborating the core idea of23, we present a protocol for cross-platform comparing spatially and temporally separated quantum processes. The protocol uses only single-qubit unitary gates and classical communication between quantum computers, without requiring quantum links or ancilla qubits. This approach allows for accurate estimation of the performance of quantum devices manufactured in separate laboratories and companies using different technologies. Furthermore, the protocol can be used to monitor the stable function of target quantum computers over time. We apply the protocol to compare the performance of five quantum devices from IBM and the “Qianshi" quantum computer from Baidu, all via the cloud. The experimental results reveal that our protocol can accurately compare the performance of arbitrary quantum processes. The numerical analysis shows that our protocol scales exponentially as \({\mathcal{O}}({2}^{bn})\) with b ≈ 2, where n is the number of qubits. This is much more favorable concerning the system size when compared to full quantum process tomography, whose scaling exponent is b ≥ 426. There are many more efficient process tomographic methods27,28,29,30. However, they either require a specific structure or a priori knowledge of the system of interest, which are not directly applicable for the cross-platform comparison task. Overall, our protocol serves as an application of the randomized measurement toolbox31.

Results

Background

Cross-platform comparison of quantum states

In quantum information, fidelity is an important metric that is widely used to characterize the closeness between quantum states. There are many different proposals for the definition of state fidelity32. In this work, we will concentrate on the max fidelity, formally defined as23,32

$$\begin{array}{r}{F}_{\max }({\rho }_{1},{\rho }_{2}):= \frac{{{{\rm{Tr}}}}[{\rho }_{1}{\rho }_{2}]}{\max \{{{{\rm{Tr}}}}[\mathop{\rho}\nolimits_{1}^{2}],{{{\rm{Tr}}}}[{\rho }_{2}^{2}]\}},\end{array}$$
(1)

where ρi is an n-qubit quantum state produced by the quantum computer, i = 1, 2.

Elben et al.23 proposed a randomized measurement protocol to estimate \({F}_{\max }\), which process is as follows. First, we construct an n-qubit unitary \(U{ = \bigotimes }_{k = 1}^{n}{U}_{k}\), where each Uk is identically and independently sampled from a single-qubit set \({\mathcal{X}}_{2}\) satisfying unitary 2-design33,34. This information will be classically communicated to the quantum computers, possibly spatially or temporally separated, that produce the quantum states ρ1 and ρ2, respectively. Then, each quantum computer executes the unitary U, performs a computational basis measurement, and records the measurement outcome s. Repeating the above procedure for fixed U a number of times, we are able to obtain two probability distributions over the outcomes of the form \(\mathop{\Pr}\nolimits_{U}^{(1)},\mathop{\Pr}\nolimits_{U}^{(2)}\), where the superscript i indicates that the distribution is obtained from quantum state ρi. Next, we repeat the whole procedure for many different random unitaries U, yielding a set of probability distributions \({\{\mathop{\Pr}\nolimits_{U}^{(1)},\mathop{\Pr}\nolimits_{U}^{(2)}\}}_{U}\). From the experimental data, we estimate the overlap between ρi and ρj as23

$$\begin{array}{r}{{{\rm{Tr}}}}[{\rho }_{i}{\rho }_{j}]={2}^{n}\mathop{\sum}\limits_{{{{\boldsymbol{s}}}},{{{{\boldsymbol{s}}}}}^{{\prime} }\in {\{0,1\}}^{n}}{(-2)}^{-{{{\mathcal{D}}}}[{{{\boldsymbol{s}}}},{{{{\boldsymbol{s}}}}}^{{\prime} }]}\overline{{\Pr }_{U}^{(i)}[{{{\boldsymbol{s}}}}]{\Pr }_{U}^{(j)}[{{{{\boldsymbol{s}}}}}^{{\prime} }]},\end{array}$$
(2)

where \(\overline{\cdots }\) denotes the ensemble average over the sampled unitaries U and \({\mathcal{D}}[{\boldsymbol{s}},{\boldsymbol{s}}^{\prime}]\) denotes the hamming distance between two bitstrings s and \({{{{\boldsymbol{s}}}}}^{{\prime} }\). Specially, \({{{\rm{Tr}}}}[{\rho }_{1}{\rho }_{2}]\) can be estimated from Eq. (2) by setting i = 1 and j = 2, whereas the purities \({{{\rm{Tr}}}}[{\rho }_{1}^{2}]\) and \({{{\rm{Tr}}}}[{\rho }_{2}^{2}]\) can be obtained by setting i = j = 1 and i = j = 2, respectively. Using the above estimated quantities, we successfully compute the max fidelity \({F}_{\max }({\rho }_{1},{\rho }_{2})\).

Using experimental data from35, Elben et al. showcased the experiment-theory fidelities and experiment-experiment fidelities of highly entangled quantum states prepared via quench dynamics in a trapped ion quantum simulator as a proof of principle23. Recently, Zhu et al. reported a thorough cross-platform comparison of quantum states in four ion-trap and five superconducting quantum platforms, with detailed analysis of the results and an intriguing machine learning approach to explore the data24.

Quantum process performance metric

A quantum process, also known as a quantum operation or a quantum channel, is a mathematical description of the evolution of a quantum system. It is mathematically formulated as a completely positive and trace-preserving (CPTP) linear map on the quantum states36. The Choi-Jamiołkowski isomorphism provides a unique way to represent quantum processes as quantum states in a larger Hilbert space. Formally, the Choi state of an n-qubit quantum process \({\mathcal{E}}\) is defined as37

$$\begin{array}{r}{\eta }_{{{{\mathcal{E}}}}}:= ({{{\mathcal{I}}}}\otimes {{{\mathcal{E}}}})\left\vert {\psi }_{+}\right\rangle \left\langle {\psi }_{+}\right\vert ,\end{array}$$
(3)

where \({\mathcal{I}}\) is the identity channel and \(\left\vert {\psi }_{+}\right\rangle := 1/\sqrt{{2}^{n}}\sum \left\vert ii\right\rangle\) is a maximally entangled state of a bipartite quantum system composed of two n-qubit subsystems.

One lesson we can learn from the cross-platform state comparison protocol is that we must choose a process metric before comparing two quantum processes. Gilchrist et al.38 introduced a systematic way to generalize a metric originally defined on quantum states to a corresponding metric on quantum processes, utilizing the Choi-Jamiołkowski isomorphism. Specifically, the max fidelity between two n-qubit quantum processes \({\mathcal{E}}_{1}\) and \({\mathcal{E}}_{2}\), implemented on different quantum platforms, is defined as

$$\begin{array}{r}{F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{{\mathcal{E}}}}}_{2}):= {F}_{\max }({\eta }_{{{{{\mathcal{E}}}}}_{1}},{\eta }_{{{{{\mathcal{E}}}}}_{2}}),\end{array}$$
(4)

where \({\eta }_{\mathcal{E}}\) is the Choi state of quantum process \({\mathcal{E}}\). Thanks to the Choi-Jamiołkowski isomorphism, this metric fulfills the axioms for process fidelities32,38, i.e., (i) \({F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{{\mathcal{E}}}}}_{2})\le 1\) with \({F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{{\mathcal{E}}}}}_{2})=1\) if and only if \({{{{\mathcal{E}}}}}_{1}={{{{\mathcal{E}}}}}_{2}\); and (ii) \({F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{{\mathcal{E}}}}}_{2})={F}_{\max }({{{{\mathcal{E}}}}}_{2},{{{{\mathcal{E}}}}}_{1})\). Thus, it can be used to verify whether two quantum devices have implemented the same quantum process.

In this work, we propose an experimentally efficient protocol to estimate this metric. This protocol makes use of only single-qubit unitaries and classical communication, thus can be executed in spatially and temporally separated quantum devices. This enables cross-platform comparison of arbitrary quantum processes.

Theories

We first provide a simple example to illustrate the necessity of cross-platform comparison. Then, we introduce a protocol for estimating the max process fidelity that is conceptually straightforward yet experimentally challenging. Next, we propose a modification to the protocol that employs randomized input states and provide a detailed explanation of the approach. Our protocol is motivated by the observation that even identical quantum computers cannot produce identical outcomes on each run due to the intrinsic randomness of quantum mechanics, but they do generate identical probability distributions from a statistical perspective.

Cross-platform comparison of quantum computers is essential for at least two reasons. Firstly, comparing the actual implementation with an idealized theoretical simulation can be challenging, especially as classical simulations become computationally demanding with an increasing number of qubits. Secondly, due to the presence of varying forms of quantum noise across different quantum platforms, the actual implementation of quantum processes can vary significantly, even if they maintain the same process fidelity with respect to the ideal target. To illustrate this point, consider the following example. Suppose Alice has a superconducting quantum computer and Bob has a trapped-ion quantum computer. They independently implement the single-qubit Hadamard gate \({\mathcal{H}}(\rho )=H\rho {H}^{\dagger}\) on their respective quantum computers. However, Alice’s implementation \({{{{\mathcal{E}}}}}_{1}\) suffers from the depolarizing noise, yielding \({{{{\mathcal{E}}}}}_{1}(\rho )=(1-{p}_{1})H\rho {H}^{{\dagger} }+{p}_{1}{\mathbb{1}}/2\), where p1 = 7/30 and \({\mathbb{1}}\) is the identity matrix. On the other hand, Bob’s implementation \({{{{\mathcal{E}}}}}_{2}\) suffers from the dephasing noise, such that \({{{{\mathcal{E}}}}}_{2}(\rho )=(1-{p}_{2})H\rho {H}^{{\dagger} }+{p}_{2}{{{\rm{{{\Delta }}}}}}(\rho )\), where p2 = 1/5 and Δ( ⋅ ) is the dephasing operation. After simple calculations, we obtain \({F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{\mathcal{H}}}})={F}_{\max }({{{{\mathcal{E}}}}}_{2},{{{\mathcal{H}}}})\approx 0.808\) and \({F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{{\mathcal{E}}}}}_{2})\approx 0.978\). Despite \({{{{\mathcal{E}}}}}_{1}\) and \({{{{\mathcal{E}}}}}_{2}\) having the same fidelity level when compared to the ideal target \({{{\mathcal{H}}}}\), a discernible difference exists between them. Therefore, solely comparing the fidelity of a quantum process to an ideal reference is insufficient, and a direct comparison between quantum processes is warranted.

Ancilla-assisted cross-platform comparison

Firstly, we propose a conceptually simple approach for estimating \({F}_{\max }\) defined in Eq. (4). The key observation is that \({F}_{\max }\) can be seen as the max state fidelity between the Choi states of the corresponding quantum processes. Hence, we can generalize the quantum state comparison protocol in the section “Cross-platform comparison of quantum states" to achieve quantum process comparison. This approach has been independently proposed in25.

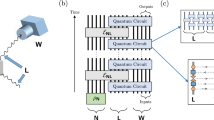
In the first step, we construct the Choi states of the target quantum process \({\mathcal{E}}\) in two quantum platforms as follows. First, we introduce an additional n-qubit clean auxiliary system in each platform. Then, we prepare a 2n-qubit maximally entangled state \(\left\vert {\psi }_{+}\right\rangle\) using the auxiliary system. Finally, we apply \({{{\mathcal{E}}}}\) to half of the whole system, successfully preparing the Choi state of \({{{\mathcal{E}}}}\). In the second step, we estimate the max state fidelity of these two Choi states using the procedure introduced in the section “Cross-platform comparison of quantum states". The complete protocol is illustrated in Fig. 1a–c.

Fig. 1: Two protocols to estimate the max process fidelity \({F}_{\max }\) between quantum processes implemented on different quantum platforms.
figure 1

a Ancilla-assisted protocol: Prepare the maximally entangled state, execute the target quantum process, and perform the randomized measurements given by \({\bigotimes }_{k = 1}^{n}{U}_{1}^{(k)}\otimes {\bigotimes }_{k = 1}^{n}{U}_{2}^{(k)}\). b Ancilla-free protocol: Randomly sample a computational basis \(\left\vert {{{\boldsymbol{s}}}}\right\rangle\), execute the unitaries \({\bigotimes }_{k = 1}^{n}{U}_{1}^{(k)T}\), execute the target quantum process, and perform the randomized measurements given by \({\bigotimes }_{k = 1}^{n}{U}_{2}^{(k)}\). c Run the quantum circuits constructed in a or b on platform \({\mathcal{S}}_{i}\) to obtain the probability distribution \(\Pr_U^{(i)}[{{{\boldsymbol{s}}}},{{{\boldsymbol{k}}}}]\). The max process fidelity \({F}_{\max }({{{{\mathcal{E}}}}}_{i},{{{{\mathcal{E}}}}}_{j})\) is inferred from the probability distributions (see text).

Full size image

We refer to this protocol as the ancilla-assisted cross-platform comparison because it requires additional clean ancilla qubits to prepare the Choi state of the quantum process. To perform this protocol, a maximally entangled state is required as input, resulting in a two-fold overhead when comparing 2n-qubit states instead of n-qubit states. Consequently, this protocol may not be practical in scenarios with limited quantum computing resources. Furthermore, preparing high-fidelity maximally entangled states can be experimentally challenging, which may negatively impact the accuracy of the protocol.

Ancilla-free cross-platform comparison

To overcome the limitations of the ancilla-assisted protocol, we propose an efficient and ancilla-free approach for estimating the max process fidelity \({F}_{\max }\). Our protocol does not require any additional qubits or the preparation of maximally entangled states. The key observation is that the auxiliary system in the ancilla-assisted protocol only needs to perform randomized measurements. After the measurement, the auxiliary system collapses to one eigenstate of the sampled measurement operator. Based on the identity \((\left\vert u\right\rangle \left\langle u\right\vert \otimes {\mathbb{1}})\left\vert {\psi }_{+}\right\rangle =\left\vert u\right\rangle \otimes \left\vert {u}^{* }\right\rangle\), where \({\mathbb{1}}\) is the identity matrix, and the deferred measurement principle39, we can eliminate the auxiliary system by preparing computational states and applying the transposed unitary operator on the main system. Please refer to Supplementary Note 1 for a detailed analysis.

We refer to this protocol as the ancilla-free cross-platform comparison and it works as follows. We consider two n-qubit quantum processes \({\mathcal{E}}_{1}\) and \({\mathcal{E}}_{2}\) realized on different quantum platforms \({{{{\mathcal{S}}}}}_{1}\) and \({{{{\mathcal{S}}}}}_{2}\), whose Choi states are η1 and η2, respectively. The protocol, illustrated in Fig. 1b–c, consists of three main steps: sampling unitaries, running circuits, and post-processing.

  1. 1.

    Sampling unitaries: Construct two n-qubit unitaries \({U}_{i}{ = \bigotimes }_{k = 1}^{n}{U}_{i}^{(k)}\), i = 1, 2, where each \({U}_{i}^{(k)}\) is identically and independently sampled from a single-qubit set \({{{{\mathcal{X}}}}}_{2}\) satisfying unitary 2-design33,34. The information of Ui is then communicated to both platforms via classical communication.

  2. 2.

    Running circuits: After receiving the information of the sampled unitaries, each platform \({\mathcal{S}}_{i}\) (i = 1, 2) initializes its quantum system to the computational states \(\left\vert {{{\boldsymbol{s}}}}\right\rangle\) and applies the first unitary U1 to \(\left\vert {{{\boldsymbol{s}}}}\right\rangle\). Subsequently, \({{{{\mathcal{S}}}}}_{i}\) implements the quantum process \({{{{\mathcal{E}}}}}_{i}\) and applies the second unitary U2. Finally, \({{{{\mathcal{S}}}}}_{i}\) performs the projective measurement in the computational basis and obtains an outcome k. Repeating the above procedure many times, we obtain two probability distributions \(\mathop{\Pr}\nolimits_{K| {{{\boldsymbol{s}}}},{U}_{1},{U}_{2}}^{(1)}\) and \(\mathop{\Pr}\nolimits_{K|{{{\boldsymbol{s}}}},{U}_{1},{U}_{2}}^{(2)}\) over the measurement outcomes k for the fixed computational state \(\left\vert {{{\boldsymbol{s}}}}\right\rangle\) and unitaries U1 and U2. By exhausting the computational states and repeatedly sampling the unitaries, we obtain two probability distributions \(\mathop{\Pr}\nolimits_{K, {S}|{U}_{1},{U}_{2}}^{(i)}\) with respect to the sampled unitaries and computational state inputs. For simplicity, we abbreviate \(\mathop{\Pr}\nolimits_{K, {S}|{U}_{1},{U}_{2}}^{(i)}\) to \(\mathop{\Pr }\nolimits_{U}^{(i)}\).

  3. 3.

    Post-processing: From the experimental data, we estimate the overlap between the Choi states ηi and ηj for i, j = 1, 2 as

    $$\begin{array}{ll}{{{\rm{Tr}}}}[{\eta }_{i}{\eta }_{j}]\,=\,{4}^{n}\mathop{\sum }\limits_{{{{\boldsymbol{s}}}},{{{{\boldsymbol{s}}}}}^{{\prime} },{{{\boldsymbol{k}}}},{{{{\boldsymbol{k}}}}}^{{\prime} }\in {\{0,1\}}^{n}}{(-2)}^{-{{{\mathcal{D}}}}[{{{\boldsymbol{s}}}},{{{{\boldsymbol{s}}}}}^{{\prime} }]-{{{\mathcal{D}}}}[{{{\boldsymbol{k}}}},{{{{\boldsymbol{k}}}}}^{{\prime} }]}\\ \qquad\qquad\times \,\overline{{\Pr }_{U}^{(i)}[{{{\boldsymbol{s}}}},{{{\boldsymbol{k}}}}]{\Pr }_{U}^{(j)}[{{{{\boldsymbol{s}}}}}^{{\prime} },{{{{\boldsymbol{k}}}}}^{{\prime} }]}.\end{array}$$
    (5)

    where \(\overline{\cdots }\) denotes the ensemble average over the sampled unitaries U1 and U2. This is proven in Supplementary Note 1. By setting i = 1 and j = 2, we can estimate the overlap \({{{\rm{Tr}}}}[{\eta }_{1}{\eta }_{2}]\) from the above equation, which is the second-order cross-correlation of the probabilities \(\mathop{\Pr }\nolimits_{U}^{(1)}\) and \(\mathop{\Pr }\nolimits_{U}^{(2)}\). We can obtain the purities \({{{\rm{Tr}}}}[{\eta }_{1}^{2}]\) and \({{{\rm{Tr}}}}[{\eta }_{2}^{2}]\) by setting i = j = 1 and i = j = 2, respectively. These are the second-order autocorrelations of the probabilities. Using the estimated quantities, we compute the max process fidelity \({F}_{\max }({{{{\mathcal{E}}}}}_{1},{{{{\mathcal{E}}}}}_{2})\) in Eq. (4).

There are several important points to note about our protocol. First, when classical simulation is available, the protocol can be used to compare the experimentally implemented process to the theoretical simulation, providing a useful tool for experiment-theory comparison. Second, our protocol can also estimate the process purity \({{{\rm{Tr}}}}[{\eta }_{{{{\mathcal{E}}}}}^{2}]\) of a quantum process \({\mathcal{E}}\), which measures the extent to which \({{{\mathcal{E}}}}\) preserves the purity of the quantum state. This is an important measure for characterizing quantum processes, and our protocol provides an efficient way to estimate it. Finally, it is worth noting that the definition of max process fidelity is not unique, and different approaches exist38,40. Our protocol, based on statistical correlations of randomized inputs and measurements, can be readily extended to any metric that depends solely on the process overlap \({{{\rm{Tr}}}}[{\eta }_{{{{{\mathcal{E}}}}}_{1}}{\eta }_{{{{{\mathcal{E}}}}}_{2}}]\) and the process purities \({{{\rm{Tr}}}}[{\eta }_{{{{{\mathcal{E}}}}}_{1}}^{2}]\) and \({{{\rm{Tr}}}}[{\eta }_{{{{{\mathcal{E}}}}}_{2}}^{2}]\). This makes our protocol highly versatile and applicable to a wide range of quantum computing scenarios.

Experiments

In this section, we report experimental results on cross-platform comparison of quantum processes across various spatially and temporally separated quantum devices. First, we demonstrate the efficacy of our protocol in comparing the H and CNOT gates implemented on different platforms with their ideal counterparts are obtained from classical simulation. Next, we use our protocol to monitor the stability of the “Qianshi" quantum computer from Baidu over a week. Finally, we conduct an extensive numerical analysis to determine the expected number of experimental runs required to obtain reliable results. All the experiments are conducted using the Quantum Error Processing toolkit developed on the Baidu Quantum Platform41.

Before presenting the experimental results, we summarize the working procedure shared among different experiments. For a target n-qubit quantum process under investigation, the protocol in the section “Ancilla-free cross-platform comparison" constitutes three steps:

  1. 1.

    Randomly sample NU number of n-qubit unitaries composed of single-qubit unitaries. Note that the random Pauli basis measurements {X, Y, Z} are equivalent to randomized measurements with a single qubit Clifford group24,42. The Clifford group is a unitary 2-design group and it can be employed to achieve complete process tomography of n-qubit quantum processes. This equivalence enables us to sample directly from the 3n Pauli preparation and 3n Pauli measurement unitaries in our experiments.

  2. 2.

    Prepare 2n number of computational basis states as inputs, evolve them with the randomly sampled unitary and the target quantum process, and measure the final state in the computational basis measurement with Mshots number of shots.

  3. 3.

    From the measurement statistics, we estimate the fidelity using Eq. (5).

The sample complexity of the above procedure is captured by the total number of experimental runs, 2n × NU × Mshots.

Comparing spatially separated quantum processes

We utilize our ancilla-free cross-platform comparison protocol to assess the performance of H and CNOT gates implemented on seven distinct platforms that are freely accessible to the public over the internet. They include six superconducting quantum computers, namely ibmq_quito (IBM_1), ibmq_oslo (IBM_2), ibmq_lima (IBM_3), ibm_nairobi (IBM_4), ibmq_manila (IBM_5), and baidu_qianshi (BD_1), as well as the baidu ideal simulator (IDEAL), which is for experiment-theory comparisons.

We set NU = 10 and Mshots = 500 to compare the performance of the single-qubit H gate across the above seven quantum platforms. Since the CNOT gate is a two-qubit gate, we set NU = 100 and Mshots = 500 to compare the performance of CNOT gate across the above seven quantum platforms. The performance matrices for the H and CNOT gates are presented in Fig. 2. The experimental results make it clear that, while some quantum devices may achieve fidelities that are comparable to those of the ideal simulator, there remains a significant discrepancy between them. This emphasizes the importance of directly comparing the performance of quantum devices with each other, rather than relying solely on comparisons to an ideal simulator, as such comparisons may not be adequate.

Fig. 2: The performance matrices for the single-qubit H and two-qubit CNOT gates generated from seven different quantum platforms.
figure 2

The entry in the i-th row and j-th column of the matrix represents the max process fidelity between platform-i and platform-j. The entries in the upper right corner are visualized in pie chart format. a The performance matrix of the H gate. Each entry is inferred from 21 ⋅ NU = 20 random circuits and each circuit is repeated Mshots = 500 times. b The performance matrix of the CNOT gate. Each entry is inferred from 22 ⋅ NU = 20 random circuits and each circuit is repeated Mshots = 500 times.

Full size image

Comparing temporally separated quantum processes

Our protocol is also useful for monitoring the stable performance of quantum devices over time. To this end, we employ the ancilla-free cross-platform comparison protocol to assess the stability of H and CNOT gates implemented on Baidu’s “Qianshi" quantum computer (BD_1) over the course of one week. The experiment is conducted every day at 14:00 and lasts about 4 hours, which is asynchronous with the daily calibration procedure usually performed at midnight. The experimental settings for the H and CNOT gates are identical to those used in the previous section. Specifically, for the single-qubit H gate, we set NU = 10 and Mshots = 500. For the two-qubit CNOT gate, we set NU = 100 and Mshots = 500. The performance matrices of the H and CNOT gates generated from the daily data of “Qianshi" are shown in Fig. 3.

Fig. 3: The performance matrices of the single-qubit H and two-qubit CNOT gates generated from the daily data of Baidu’s “Qianshi" quantum computer for one week.
figure 3

The entry in the i-th row and j-th column of the matrix represents the max process fidelity between platform-i and platform-j. The entries in the upper right corner are visualized in pie chart format. a The performance matrix of the H gate. Each entry is inferred from 21 ⋅ NU = 20 random circuits and each circuit is repeated Mshots = 500 times. b The performance matrix of the CNOT gate. Each entry is inferred from 22 ⋅ NU = 400 random circuits and each circuit is repeated Mshots = 500 times.

Full size image

After analyzing the cross-platform fidelities presented in Fig. 3, we discover several noteworthy features. First, we observe that the stability of the H gate is considerably higher than that of the CNOT gate on “Qianshi," which aligns with the expectation that two-qubit gates are harder to implement and maintain in a superconducting quantum computer than single-qubit gates. Additionally, on the last day of the week (DAY_7), there is a significant drop in the performance of the CNOT gate. After consulting with researchers from Baidu’s Quantum Computing Hardware Laboratory, it is determined that the instability is caused by the sudden halt of the dilution cooling system. After the system is restarted, all native quantum gates have to be re-calibrated to achieve optimal performance. Furthermore, it is observed that the temperature variation had a negligible impact on the H gate. This observation might be helpful for the experimenters to identify potential hardware issues.

Scaling of the required number of experimental runs

In practice, the accuracy of the estimated fidelity is unavoidably subject to statistical error, as a result of the finite number of random circuits (2n × NU) and the finite number of computational basis measurements (Mshots) performed per random circuit. Therefore, it is experimentally crucial to consider the scaling of the total number of experimental runs 2n × NU × Mshots, which represents the measurement budget, in order to effectively suppress the statistical error to a prespecified threshold ϵ when evaluating the performance of an n-qubit quantum process. In the following, we present numerical simulation to investigate this behavior.

In Fig. 4, numerical results for the average statistical error as a function of the measurement budget 2n × NU × Mshots are presented, and the scaling of the measurement budget with respect to the system size n is derived. In order to keep consistent with previous experiments, we choose the H gate when n = 1 and the CNOT gate when n = 2 in the simulation. Note that in this case the ideal fidelity \({F}_{\max }=1\) is known. We repeat our protocol on the ideal simulator 5 times for each point in the figure and record the mean of the statistical errors \(| {\widetilde{F}}_{\max }-1.0|\). We find that the statistical error scales as \(| {\widetilde{F}}_{\max }-1.0| \sim 1/({2}^{n}{N}_{U}{M}_{{{{\rm{shots}}}}})\), where \({\widetilde{F}}_{\max }\) is the estimated max process fidelity via simulation.

Fig. 4: Average statistical error \(| {\widetilde{F}}_{\max }-1|\) as a function of the total number of experimental runs 2nNUMshots.
figure 4

The target quantum process is taken to be the H gate for n = 1 and the CNOT gate for n = 2. The green lines obey ~ 1/(2nNUMshots) and are guides for the eye. The data are obtained via numerical simulation.

Full size image

Now we investigate the scaling of the required number of experimental runs, 2n × Mshots, per unitary to estimate the max fidelity \({\widetilde{F}}_{\max }\) within an average statistical error of ϵ = 0.05 while fixing NU to 100. We employ our protocol to two very different types of quantum processes with different numbers of qubits n: (i) a highly entangled quantum process corresponding to an n-qubit GHZ state preparation circuit (Entangled) and (ii) a completely local quantum process composed of n single-qubit rotation gates (Non-Entangled). The numerical results are presented in Fig. 5. From the fitted data, we observe that 2n × Mshots ~ 2bn, where b = 2.05 ± 2e-5 for the entangled case and b = 1.89 ± 2e-4 for the non-entangled case. This scaling analysis closely aligns with the previous findings in cross-platform state comparisons23 and reveals that the sample complexity of our ancilla-free cross-platform protocol scales as \({2}^{n}\times {N}_{U}\times {M}_{\rm{shots}} \sim {\mathcal{O}}({2}^{bn})\) with b ≈ 2. This scaling, although exponential, is significantly better than full quantum process tomography (QPT), which has an exponent b ≥ 426.

Fig. 5: Scaling of the minimal number of required experimental runs 2nMshots to estimate \({\widetilde{F}}_{\max }\) up to a fixed statistical error of 0.05 as a function of the number of qubits n.
figure 5

The number of random unitaries is fixed to NU = 100. The target quantum process is taken to be the n-qubit GHZ state preparation circuit for the entangled case and the rotation circuit composed of n single-qubit rotation gates for the non-entangled case. The data is obtained via numerical simulation and the error bars are generated from five independent experiments.

Full size image

Discussion

We have proposed an ancilla-free cross-platform protocol that enables the performance comparison of arbitrary quantum processes using only single-qubit unitaries and classical communication. This protocol is suitable for comparing quantum processes that are independently manufactured over different times and locations, built by different teams using different technologies. We have experimentally demonstrated the cross-platform protocol on six remote quantum computers fabricated by IBM and Baidu, and monitored the stable functioning of Baidu’s “Qianshi" quantum computer over one week. The experimental results reveal that our protocol accurately compares the performance of different quantum computers with significantly fewer measurements than quantum process tomography. Additionally, we have shown that our protocol applies to quantum process tomography.

However, some problems must be further explored to make the cross-platform protocols more practical. Firstly, the sample complexity of these protocols lacks theoretical guarantees, necessitating the empirical selection of experimental parameters. References43,44 might be a good starting point for addressing this challenge, where the authors gave analytically scaling law of the statistical errors with global random unitaries. Secondly, it is vital to make the protocols robust against state preparation and measurement errors. One possible solution is to apply quantum error mitigation methods45,46,47,48,49 to alleviate quantum errors and increase the estimation accuracy. We suggest that ideas from randomized benchmarking21 and quantum gateset tomography50 might also be helpful for designing error robust cross-platform protocols.

Methods

Randomized quantum process tomography

Here we show that the protocols proposed in the “Results" section can be utilized to achieve full quantum process tomography. This idea is motivated by Ref. 51, in which they proposed a method for performing full quantum state tomography using randomized measurements.

For an n-qubit quantum process \({\mathcal{E}}\), we can first construct the Choi state of \({{{\mathcal{E}}}}\) and then use the proposed protocol to obtain the full information of the Choi state \({\eta }_{{{{\mathcal{E}}}}}\). However, as previously mentioned, this method is inefficient and is impractical due to the imperfect preparation of maximally entangled states and the requirement for an additional n-qubit auxiliary system. Likewise, we may use the randomized input states trick introduced in the section “Ancilla-free cross-platform comparison" to overcome the above issues. Specifically, based on the experimental data \({{\rm{P{r}}}_{U}}\) collected in the section “Ancilla-free cross-platform comparison", the complete information of an unknown n-qubit quantum process \({{{\mathcal{E}}}}\) can be obtained via

$$\begin{array}{ll}{\eta }_{{{{\mathcal{E}}}}}\,=\,{4}^{n}\mathop{\sum }\limits_{{{{\boldsymbol{s}}}},{{{{\boldsymbol{s}}}}}^{{\prime} },{{{\boldsymbol{k}}}},{{{{\boldsymbol{k}}}}}^{{\prime} }\in {\{0,1\}}^{n}}{(-2)}^{-{{{\mathcal{D}}}}[{{{\boldsymbol{s}}}},{{{{\boldsymbol{s}}}}}^{{\prime} }]-{{{\mathcal{D}}}}[{{{\boldsymbol{k}}}},{{{{\boldsymbol{k}}}}}^{{\prime} }]}\\ \qquad\times \,\overline{{\Pr }_{U}[{{{\boldsymbol{s}}}},{{{\boldsymbol{k}}}}]{U}^{{\dagger} }\left\vert {{{{\boldsymbol{s}}}}}^{{\prime} }{{{{\boldsymbol{k}}}}}^{{\prime} }\right\rangle \left\langle {{{{\boldsymbol{s}}}}}^{{\prime} }{{{{\boldsymbol{k}}}}}^{{\prime} }\right\vert U},\end{array}$$
(6)

where U = U1 ⊗ U2 and \(\overline{\cdots }\) denotes the ensemble average over the sampled unitaries U1 and U2 as before. This is proven in Supplementary Note 2.

Comparison with previous works

Knörzer et al.25 have recently introduced a set of protocols that enable pair-wise comparisons between distant nodes in a quantum network. Their contributions are twofold. First, they proposed four cross-platform state comparison schemes as alternatives to Elben’s protocol23, each relying on the presence of quantum links. Second, based on these state comparison protocols, they designed three cross-platform quantum process comparison protocols M1, M2, and M3.

We explain how our process comparison protocols differ from M1, M2, and M3. While M1 involves an ancilla-assisted comparison protocol that we have rephrased in the section “Ancilla-assisted cross-platform comparison", our protocol does not rely on ancilla qubits. M3 involves a series of entanglement tests that are fundamentally different from our protocol. M2 and our protocol do share similarities, such as the absence of ancilla qubits and the need to sample random unitaries and computational basis states, but there are notable differences. Specifically, our protocol only samples from a single-qubit unitary 2-design and accurately estimates the max fidelity. On the other hand, M2(i) estimates the average gate fidelity and requires sampling from a multi-qubit unitary 2-design, which can be resource-intensive as the number of qubits increases. M2(iii) is conceptually straightforward but its estimated quantity is basis-dependent, while the other fidelities investigated in this paper are all basis-independent. Additionally, M2(i) and M2(iii) are limited to comparing the performance of unitary quantum processes.