Approximating outcome probabilities of linear optical circuits

Abstract

Quasiprobability representations are important tools for analyzing a quantum system, such as a quantum state or a quantum circuit. In this work, we propose classical algorithms specialized for approximating outcome probabilities of a linear optical circuit using quasiprobability distributions. Notably, we can reduce the negativity bound of a circuit from exponential to at most polynomial for specific cases by modulating the shapes of quasiprobability distributions thanks to the symmetry of the linear optical transformation in the phase space. Consequently, our scheme provides an efficient estimation of outcome probabilities within an additive-error whose precision depends on the classicality of the input state. When the classicality is high enough, we reach a polynomial-time estimation algorithm of a probability within a multiplicative-error by an efficient sampling from a log-concave function. By choosing appropriate input states and measurements, our results provide plenty of quantum-inspired classical algorithms for approximating various matrix functions beating best-known results. Moreover, we give sufficient conditions for the classical simulability of Gaussian Boson sampling using our approximating algorithm for any (marginal) outcome probability under the poly-sparse condition.

introduction

Quantum computers are believed to provide significant advantages in solving computational problems beyond classical power^1,2. Despite the potential advantage, determining which types of quantum circuits are classically simulable is still a longstanding open problem. A viable approach for the problem is to examine quasiprobability distributions in the phase space, a standard method in quantum optics³. Specifically, on the one hand, if the output distributions of a quantum circuit can be described by non-negative quasiprobability distributions, there is a classically efficient simulation of the circuit⁴. On the other hand, one can estimate the outcome probabilities of a quantum circuit with the convergence rate depending on the negativity bound of the circuit, a measure of negativity in the phase space⁵. In both cases, the negativity of quasiprobability distributions plays a crucial role, which has been extensively studied^6,7,8,9.

Meanwhile, boson sampling has recently attracted lots of attention due to its feasible quantum advantage using a linear optical circuit^{10,11,12,13,14}. Also, there have been numerous studies of boson sampling using quasiprobability distributions^{15,16,17,18,19}. In particular, while Fock-state and Gaussian Boson sampling (GBS) are believed to be hard to classically simulate^10,20, boson sampling with a classical state input, represented by a nonnegative P-function, is efficiently simulated because its output distribution can be expressed by nonnegative quasiprobability distributions¹⁶. Interestingly, this quantum optical observation leads to the fact that the permanent of Hermitian positive-semidefinite (HPSD) matrices can be approximated within a multiplicative-error more easily (in BPP^NP) than that of arbitrary matrices (#P-hard)^15,21. In addition, a quantum-inspired algorithm using quasiprobability distributions has been proposed for estimating the permanent of an HPSD matrix within an additive-error, which outperforms Gurvits’ algorithm under certain eigenvalue conditions^22,23. Thus, studying the quasiprobability representation of quantum circuits often provides new insight into computational problems.

However, previous studies are limited to the cases of classical input states with no negativity^15,16,18,23 or negativity bound that is polynomial in the system size⁵, which cannot cover typical quantum circuits with exponential negativity bound. A central question is how to generalize the quasiprobability methods to handle cases of exponential negativity bound. Such a generalization can also lead to improved quantum-inspired algorithms for approximating matrix functions, e.g., permanent and hafnian. Moreover, it is still open to finding an efficient algorithm for the multiplicative-error approximation of a matrix function beyond the method using sampling from nonnegative quasiprobability distributions¹⁵. Since a multiplicative-error approximation is significantly more powerful than an additive-error one and only a few examples have been known^24,25,26, such findings have interesting applications in computational complexity.

In this work, we provide algorithms specialized for approximating the outcome probabilities of a linear optical circuit. First, we choose the s-parameterized quasiprobability distributions (s-PQDs), a generalization of P-, Q-, and Wigner distributions²⁷. An advantage of adopting s-PQDs over previous approaches is that we can always obtain a nonnegative representation for a Gaussian input state by choosing an appropriate parameter s. Consequently, for a GBS circuit, we can significantly reduce the negativity bound of the circuit, which depends only on the maximum peak of the s-PQDs of measurement operators. Furthermore, the negativity bound is determined by the maximum possible s, called classicality of the input Gaussian state²⁸, which has a clear physical meaning: the more classicality in the input state, the lower negativity bound.

Our main technical contribution is to provide a way of manipulating the shape of s-PQDs using the symmetry of the circuit transformation in the phase space. This method can considerably lower the negativity bound, from exponential to at most polynomial in several cases, which renders efficient estimations of outcome probabilities within 1/poly additive-error. Strikingly, when the classicality of the input state is high enough, we introduce a fully polynomial-time randomized approximation scheme (FPRAS) by an efficient sampling from a log-concave function^26,29, which can efficiently (in BPP) approximate the corresponding outcome probability within a multiplicative-error.

Our results have several intriguing applications to problems in computational complexity. First, we give estimating algorithms with additive-errors for matrix functions represented by the outcome probabilities of a linear optical circuit, beating the best-known classical algorithms, e.g., the hafnian of a complex symmetric matrix and the permanent of an HPSD matrix. Second, we provide efficient multiplicative-error algorithms for those matrix functions with certain structured matrices, which are not considered in the literature to the best of our knowledge. Last but not least, we present sufficient conditions on the classical simulability of GBS, by applying our estimation scheme to any (marginal) outcome probability of a GBS circuit with 1/poly additive-error under a poly-sparsity condition.

Let us consider the Born rule probabilities of a quantum optical circuit using quasiprobability distributions in the phase space. For an M-mode input state ρ_in, a quantum channel ${{{\mathcal{E}}}}$, and a measurement Π_ν, the probability for a measurement outcome ν ≔ (ν₁, …, ν_M) can be written as¹⁶

$$\begin{array}{l}p({{{\boldsymbol{\nu }}}})\,=\,{\pi }^{M}\displaystyle{\int}{d}^{2M}{{{\boldsymbol{\alpha }}}}{d}^{2M}{{{\boldsymbol{\beta }}}}{W}_{{\rho }_{{{{\rm{in}}}}}}^{(t)}({{{\boldsymbol{\alpha }}}}){T}_{{{{\mathcal{E}}}}}^{(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}}){W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{(-s)}({{{\boldsymbol{\beta }}}}),\end{array}$$

(1)

where ${W}_{{\rho }_{{{{\rm{in}}}}}}^{(t)}({{{\boldsymbol{\alpha }}}}),{W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{(-s)}({{{\boldsymbol{\beta }}}})$, and ${T}_{{{{\mathcal{E}}}}}^{(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})$ are s-PQDs of the input state, measurement, and the transition function of the circuit channel, respectively. Here, α is a quadrature variable in the 2M-dimensional phase space and β is a transformed quadrature variable by the transition function ${T}_{{{{\mathcal{E}}}}}^{(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})$. Specifically, ${W}_{\rho }^{(s)}({{{\boldsymbol{\alpha }}}})$ is the s-PQD for a Hermitian operator ρ defined by

$${W}_{\rho }^{(s)}({{{\boldsymbol{\alpha }}}})=\int\frac{{d}^{2M}{{{{\boldsymbol{\alpha }}}}}^{{\prime} }}{{\pi }^{2M}}\,{{\mbox{Tr}}}\,[\rho D({{{{\boldsymbol{\alpha }}}}}^{{\prime} })]{e}^{{{{{\boldsymbol{\alpha }}}}}^{{\prime} }s{{{{\boldsymbol{\alpha }}}}}^{{\prime} {\dagger} }/2}{e}^{{{{\boldsymbol{\alpha }}}}{{{{\boldsymbol{\alpha }}}}}^{{\prime} {\dagger} }-{{{{\boldsymbol{\alpha }}}}}^{{\prime} }{{{{\boldsymbol{\alpha }}}}}^{{\dagger} }},$$

(2)

where $D({{{{\boldsymbol{\alpha }}}}}^{{\prime} })={e}^{{{{{\boldsymbol{\alpha }}}}}^{{\prime} }{\hat{{{{\boldsymbol{a}}}}}}^{{\dagger} }-\hat{{{{\boldsymbol{a}}}}}{{{{\boldsymbol{\alpha }}}}}^{{\prime} {\dagger} }}$ is the M-mode displacement operator. Note that s = − 1, 0, 1 of s-PQDs correspond to the Q-, Wigner, and P-distribution, respectively. Also, ( − s)-PQDs of the measurement operators satisfy the normalization condition such that ${\pi }^{M}{\sum }_{{{{\boldsymbol{\nu }}}}}{W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{(-s)}({{{\boldsymbol{\beta }}}})=1$ for any β. The transition function of a quantum channel ${{{\mathcal{E}}}}$ is defined by¹⁶

$$\begin{array}{l}{T}_{{{{\mathcal{E}}}}}^{(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})\,=\,\displaystyle{\int}\frac{{d}^{2M}{{{\boldsymbol{\zeta }}}}}{{\pi }^{2M}}{e}^{{{{\boldsymbol{\zeta }}}}{{{\boldsymbol{s}}}}{{{{\boldsymbol{\zeta }}}}}^{{\dagger} }/2}{e}^{{{{\boldsymbol{\beta }}}}{{{{\boldsymbol{\zeta }}}}}^{{\dagger} }-{{{\boldsymbol{\zeta }}}}{{{{\boldsymbol{\beta }}}}}^{{\dagger} }}\\ \qquad\qquad\qquad \times \displaystyle{\int}\frac{{d}^{2M}{{{\boldsymbol{\xi }}}}}{{\pi }^{M}}{e}^{-{{{\boldsymbol{\xi }}}}{{{\boldsymbol{t}}}}{{{{\boldsymbol{\xi }}}}}^{{\dagger} }/2}{e}^{{{{\boldsymbol{\xi }}}}{{{{\boldsymbol{\alpha }}}}}^{{\dagger} }-{{{\boldsymbol{\alpha }}}}{{{{\boldsymbol{\xi }}}}}^{{\dagger} }}\,{{\mbox{Tr}}}\,\left[{{{\mathcal{E}}}}({D}^{{\dagger} }({{{\boldsymbol{\xi }}}}))D({{{\boldsymbol{\zeta }}}})\right],\end{array}$$

(3)

where

$${{{\mathcal{E}}}}({D}^{{\dagger} }({{{\boldsymbol{\xi }}}}))={e}^{{{{\boldsymbol{\xi }}}}{{{{\boldsymbol{\xi }}}}}^{{\dagger} }/2}\int\frac{{d}^{2M}{{{\boldsymbol{\gamma }}}}}{{\pi }^{M}}{e}^{{{{\boldsymbol{\gamma }}}}{{{{\boldsymbol{\xi }}}}}^{{\dagger} }-{{{\boldsymbol{\xi }}}}{{{{\boldsymbol{\gamma }}}}}^{{\dagger} }}{{{\mathcal{E}}}}(\left\vert {{{\boldsymbol{\gamma }}}}\right\rangle \left\langle {{{\boldsymbol{\gamma }}}}\right\vert ),$$

(4)

for a coherent state $\left\vert {{{\boldsymbol{\gamma }}}}\right\rangle$. In this work, we are concerned with a linear optical circuit represented by a unitary matrix U with a product input state ${\rho }_{{{{\rm{in}}}}}={\otimes }_{i = 1}^{M}{\rho }_{i}$ and a product measurement ${{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}={\otimes }_{j = 1}^{M}\left\vert {\nu }_{j}\rangle \langle {\nu }_{j}\right\vert$. In that case, if we choose t = s, then the transition function becomes a simple form such as ${T}_{{{{\mathcal{E}}}}}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})=\delta ({{{\boldsymbol{\beta }}}}-U{{{\boldsymbol{\alpha }}}})$. Consequently, Eq. (1) can be written in the simpler form

$$\begin{array}{l}p({{{\boldsymbol{\nu }}}})\,=\,{\pi }^{M}\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}\mathop{\prod }\limits_{i=1}^{M}{W}_{{\rho }_{i}}^{(s)}({\alpha }_{i})\mathop{\prod }\limits_{j=1}^{M}{W}_{{{{\Pi }}}_{{\nu }_{j}}}^{(-s)}({\beta }_{j}),\end{array}$$

(5)

where ${\beta }_{i}=\mathop{\sum }\nolimits_{j = 1}^{M}{U}_{ji}{\alpha }_{j}$ by the transition function. Suppose we have a product Gaussian input state with the covariance matrix V_i and a product photon number measurement ${{{\Pi }}}_{{m}_{j}}$. The s-PQD of a single-mode Gaussian state with zero-displacement having covariance matrix V is given by³⁰

$${W}_{V}^{(s)}({{{\boldsymbol{\alpha }}}})=\frac{\exp \left[-{{{\boldsymbol{\alpha }}}}{(V-s{{\mathbb{I}}}_{2}/2)}^{-1}{{{{\boldsymbol{\alpha }}}}}^{T}\right]}{\pi \sqrt{\det (V-s{{\mathbb{I}}}_{2}/2)}}.$$

(6)

Note that for any physical covariance matrix V, there exists a critical value ${s}_{\max }$ such that ${W}_{V}^{(s)}({{{\boldsymbol{\alpha }}}})$ is a proper Gaussian distribution for $s < {s}_{\max }$ and has a delta function singularity for $s={s}_{\max }$¹⁸. We call ${s}_{\max }$ “classicality” of the Gaussian input state²⁸. Meanwhile, the (−s)-PQD for the photon number measurement operator $\left\vert m\right\rangle \left\langle m\right\vert$ can be represented^9,31 as

$${W}_{{{{\Pi }}}_{m}}^{(-s)}({{{\boldsymbol{\beta }}}})=\frac{2}{\pi (s+1)}{\left(\frac{s-1}{s+1}\right)}^{m}{{{\mbox{L}}}}_{m}\left(\frac{4| {{{\boldsymbol{\beta }}}}{| }^{2}}{1-{s}^{2}}\right){e}^{-\frac{2| {{{\boldsymbol{\beta }}}}{| }^{2}}{s+1}},$$

(7)

where L_m(x) is the m^th Laguerre polynomial and s > − 1.

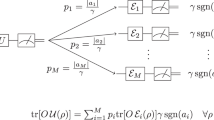
The first method is to estimate the Born rule probability within an additive-error. From the result in ref. ⁵, one can estimate the outcome probability p(ν) within error ϵ with success probability 1 − δ for a given number of samples $N=\frac{2{{{{\mathcal{M}}}}}_{\to }^{2}}{{\epsilon }^{2}}\log \frac{2}{\delta }$. Here, ${{{{\mathcal{M}}}}}_{\to }$ is the (forward) negativity bound of the circuit defined as

$${{{{\mathcal{M}}}}}_{\to }=\mathop{\prod }\limits_{i=1}^{M}{{{{\mathcal{M}}}}}_{{\rho }_{i}}\mathop{\prod }\limits_{j=1}^{M}\mathop{\max }\limits_{{\beta }_{j}}\left\vert {W}_{{{{\Pi }}}_{{\nu }_{j}}}^{(-s)}({\beta }_{j})\right\vert ,$$

(8)

where ${{{{\mathcal{M}}}}}_{{\rho }_{i}}=\int{d}^{2}{\alpha }_{i}\vert {W}_{{\rho }_{i}}^{(s)}({\alpha }_{i})\vert$ is the negativity of the state ρ_i in the phase space. When the negativity bound ${{{{\mathcal{M}}}}}_{\to }$ increases at most polynomially in the number of modes M, we can efficiently estimate the corresponding outcome probability with additive-error ϵ within running time $T=\,{{\mbox{poly}}}\,(M,1/\epsilon ,\log {\delta }^{-1})$.

Although this method is generally applicable for circuits having negativity, we usually encounter exponential negativity bound, i.e., ${{{{\mathcal{M}}}}}_{\to }={c}^{M}$ with c > 1, due to the input state negativity or a high maximum peak of the quasiprobability distribution of the measurement part. To circumvent this problem, finding a good quasiprobability representation for a given circuit with a small negativity is critical³². For instance, let us consider a GBS circuit with the input of a pure squeezed vacuum state and photon number measurement. By choosing s-PQDs, the negativity of the input state is removed when $s\le {s}_{\max }$. However, the negativity bound is still exponential in the number of modes because of the high peaks of s-PQDs for the measurement operators except for a small squeezing parameter.

Remarkably, for special cases, we can reach a much stronger approximation, namely FPRAS. An FPRAS can estimate the target function p(ν) within a multiplicative-error ϵ, which means for any 0 < ϵ < 1, 0 < δ < 1, the algorithm outputs μ such that

$$\,{{\mbox{Pr}}}\,[(1-\epsilon )p({{{\boldsymbol{\nu }}}})\le \mu \le (1+\epsilon )p({{{\boldsymbol{\nu }}}})]\ge 1-\delta ,$$

(9)

with the running time $\,{{\mbox{poly}}}\,(M,1/\epsilon ,\log {\delta }^{-1})$. A sufficient condition for FPRAS is that the target function can be written as an integral of a log-concave function f(t), i.e., $\log f(\theta x+(1-\theta )y)\ge \theta \log f(x)+(1-\theta )\log f(y)$ for all x, y and 0 < θ < 1, such that $p({{{\boldsymbol{\nu }}}})={\int}_{{{\mathbb{R}}}^{2M}}f(t)dt$^26,29. Let us consider a linear optical circuit as in Eq. (5). Since a multivariate Gaussian distribution is log-concave, s-PQD of a Gaussian input state fulfills the condition of log-concavity. If we choose a Gaussian measurement, the integrand satisfies the log-concavity but it is a trivial case. In this work, we develop a technique for making the quasiprobability of a non-Gaussian measurement log-concave, by manipulating quasiprobability in the phase space. The main results are the following:

• Our key technique for manipulating quasiprobability distribution in the phase space

• Scheme for additive/multiplicative-errors approximations of outcome probabilities of a linear optical circuit depending on the parameter regime

• Providing additive-error approximation algorithms for various matrix functions beating best-known classical algorithms, such as the hafnian of a complex symmetric matrix (Theorem 1) and the permanent of HPSD matrix (Theorem 2)

• Providing multiplicative-error approximation algorithms for various matrix functions, such as the hafnian of a structured matrix (Theorem 3)

• Sufficient conditions for the efficient simulability of lossy GBS under a poly-sparsity assumption (Theorem 4)

We summarize additive- and multiplicative-errors quantum-inspired algorithms for various matrix functions including Torontonian in Supplementary Table I.

Results

Manipulating quasiprobability in the phase space

In the previous section, we introduced two approximation schemes for the Born rule probability of an optical circuit. Those methods themselves do not seem to give powerful results for physically relevant situations. To obtain more interesting results, we propose a method manipulating the shapes of quasiprobability distributions using the symmetry of circuit transformation in the phase space.

In a general situation, one can rewrite the Born rule probability Eq. (1) as

$$\begin{array}{l}p({{{\boldsymbol{\nu }}}})\,=\,{\pi }^{M}\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}{d}^{2M}{{{\boldsymbol{\beta }}}}{W}_{{\rho }_{{{{\rm{in}}}}}}^{(t)}({{{\boldsymbol{\alpha }}}}){T}_{{{{\mathcal{E}}}}}^{(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}}){W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{(-s)}({{{\boldsymbol{\beta }}}})\\ \qquad\,\,=\,{\pi }^{M}\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}{d}^{2M}{{{\boldsymbol{\beta }}}}{W}_{{\rho }_{{{{\rm{in}}}}}}^{(t)}({{{\boldsymbol{\alpha }}}})h({{{\boldsymbol{\alpha }}}}){{T}^{{\prime}(t,s)}_{U}}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})\end{array}$$

(10)

$$\times g({{{\boldsymbol{\beta }}}}){W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{(-s)}({{{\boldsymbol{\beta }}}})$$

(11)

$$:= {\pi }^{M}\int{d}^{2M}{{{\boldsymbol{\alpha }}}}{d}^{2M}{{{\boldsymbol{\beta }}}}{W}_{{\rho }_{{{{\rm{in}}}}}}^{{}^{{\prime} }(t)}({{{\boldsymbol{\alpha }}}}){T}_{U}^{{}^{{\prime} }(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}}){W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{{}^{{\prime} }(-s)}({{{\boldsymbol{\beta }}}}),$$

(12)

where ${W^{{\prime}(t)}_{{\rho }_{{{{\rm{in}}}}}}({{{\boldsymbol{\alpha }}}})}={W}_{{\rho }_{{{{\rm{in}}}}}}^{(t)}({{{\boldsymbol{\alpha }}}})h({{{\boldsymbol{\alpha }}}})$ and ${{W}^{{\prime}(-s)}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}}({{{\boldsymbol{\beta }}}})={W}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}^{(-s)}({{{\boldsymbol{\beta }}}})g({{{\boldsymbol{\beta }}}})$ with appropriate functions h(α) and g(β). For the second equality, the transition function should satisfy a condition resulting by a symmetry in the phase space, which is given by

$${T}_{{{{\mathcal{E}}}}}^{(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})=h({{{\boldsymbol{\alpha }}}}){{T}^{{\prime}(t,s)}_{U}}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})g({{{\boldsymbol{\beta }}}}),$$

(13)

Here, the auxiliary functions h(α) and g(β) have to be chosen so that the modified functions ${W}_{{\rho }_{{{{\rm{in}}}}}}^{{}^{{\prime} }(t)}({{{\boldsymbol{\alpha }}}}),{T}_{U}^{{}^{{\prime} }(t,s)}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})$, and ${{W}^{{\prime}(-s)}_{{{{\Pi }}}_{{{{\boldsymbol{\nu }}}}}}}({{{\boldsymbol{\beta }}}})$ are well behaved in the phase space. An important point is that the modified functions do not need to be proper quasiprobability distributions of physical operators because we only need to exploit their shapes in the phase space. Consequently, these additional degrees of freedom allow us to further optimize the shapes of s-PQDs for our purposes.

Let us consider the linear optical setting. For t = s, with transition function T_U(β∣α) = δ(β − Uα), one can choose the modified function ${T}_{U}^{{\prime} }({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})={T}_{U}({{{\boldsymbol{\beta }}}}| {{{\boldsymbol{\alpha }}}})$ with $h({{{\boldsymbol{\alpha }}}})={e}^{\gamma | {{{\boldsymbol{\alpha }}}}{| }^{2}},g({{{\boldsymbol{\beta }}}})={e}^{-\gamma | {{{\boldsymbol{\beta }}}}{| }^{2}}$ with an appropriate constant γ. For this choice, we exploit the norm-preserving symmetry of linear optical transformation in the phase space, i.e., ∣α∣² = ∣β∣², and the product form of s-PQDs. As a result, the Born rule probability is rewritten as

$$\begin{array}{l}p({{{\boldsymbol{\nu }}}})\,=\,{\pi }^{M}\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}{d}^{2M}{{{\boldsymbol{\beta }}}}\mathop{\prod }\limits_{i=1}^{M}{W}_{{V}_{i}}^{(s)}({\alpha }_{i})\delta ({{{\boldsymbol{\beta }}}}-{{{\boldsymbol{U}}}}{{{\boldsymbol{\alpha }}}})\\ \qquad\quad \times \,\mathop{\prod }\limits_{j=1}^{M}{W}_{{{{\Pi }}}_{{m}_{j}}}^{(-s)}({\beta }_{j})\\ \qquad\quad=\,{\pi }^{M}\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}{d}^{2M}{{{\boldsymbol{\beta }}}}\mathop{\prod }\limits_{i=1}^{M}{W}_{{V}_{i}}^{(s)}({\alpha }_{i}){e}^{\gamma | {{{\boldsymbol{\alpha }}}}{| }^{2}}\delta ({{{\boldsymbol{\beta }}}}-{{{\boldsymbol{U}}}}{{{\boldsymbol{\alpha }}}})\end{array}$$

(14)

$$\times {e}^{-\gamma | {{{\boldsymbol{\beta }}}}{| }^{2}}\mathop{\prod }\limits_{j=1}^{M}{W}_{{{{\Pi }}}_{{m}_{j}}}^{(-s)}({\beta }_{j})$$

(15)

$$={\pi }^{M}\int{d}^{2M}{{{\boldsymbol{\alpha }}}}\mathop{\prod }\limits_{i=1}^{M}{W}_{{V}_{i}}^{(s)}({\alpha }_{i}){e}^{\gamma | {\alpha }_{i}{| }^{2}}\mathop{\prod }\limits_{j=1}^{M}{e}^{-\gamma | {\beta }_{j}{| }^{2}}{W}_{{{{\Pi }}}_{{m}_{j}}}^{(-s)}({\beta }_{j})$$

(16)

$$:= \int{d}^{2M}{{{\boldsymbol{\alpha }}}}\mathop{\prod }\limits_{i=1}^{M}{P}_{i}({\alpha }_{i},{V}_{i},s,\gamma )\mathop{\prod }\limits_{j=1}^{M}{f}_{j}({\beta }_{j},{{{\Pi }}}_{{m}_{j}},s,\gamma ),$$

(17)

where ${P}_{i}({\alpha }_{i},{V}_{i},s,\gamma )=\frac{1}{{{{{\mathcal{N}}}}}_{i}}{W}_{{V}_{i}}^{(s)}({\alpha }_{i}){e}^{\gamma | {\alpha }_{i}{| }^{2}}$ with appropriate normalization constants ${{{{\mathcal{N}}}}}_{i}$ satisfying ∫ d²α_iP_i(α_i, V_i, s, γ) = 1, and ${f}_{j}({\beta }_{j},{{{\Pi }}}_{{m}_{j}},s,\gamma )={{{{\mathcal{N}}}}}_{j}{e}^{-\gamma | {\beta }_{j}{| }^{2}}{W}_{{{{\Pi }}}_{{m}_{j}}}^{(-s)}({\beta }_{j})$ with ${{{{\mathcal{N}}}}}_{i}={{{{\mathcal{N}}}}}_{j}$, for i = j.

Improved approximations of outcome probabilities

Let us first focus on improving the approximation scheme with additive-error using our method. Since P_i(α_i, V_i, s, γ)’s are nonnegative distributions for a Gaussian input state, the modified negativity bound is given by ${{{{\mathcal{M}}}}}_{\to }^{{\prime} }=\mathop{\prod }\nolimits_{j = 1}^{M}\mathop{\max }\nolimits_{{\beta }_{j}}\left\vert {f}_{j}({\beta }_{j},{{{\Pi }}}_{{m}_{j}},s,\gamma )\right\vert$. The advantage of our method is manifest especially when ${{{{\mathcal{M}}}}}_{\to }$ grows exponentially in the number of modes whereas ${{{{\mathcal{M}}}}}_{\to }^{{\prime} }$ grows at most polynomially in the number of modes (see Fig. 1b). Let us present a simple example for which our method works well. Consider an M-mode identical pure squeezed vacuum states input with squeezing parameter r > 0 and all single-photon outcomes m = (1, …, 1). Since the negativity of the photon number measurement operator is monotonically decreasing with growing s, we choose $s={s}_{\max }={e}^{-2r}$ ²⁸. Then the negativity bound ${{{{\mathcal{M}}}}}_{\to }$ is exponential in M when the squeezing is high, i.e., $r \,> \,\frac{1}{2}\log (2+\sqrt{5})$, because of $\mathop{\max }\nolimits_{{\beta }_{j}}\vert {W}_{{{{\Pi }}}_{1}}^{(-{s}_{\max })}({\beta }_{j})\vert > 1$. However, we can shift the Gaussian factor by choosing γ as (see Supplementary Note 1)

$${\gamma }^{* }=(1+\tanh r)\left[(1+\coth r)W(1/e)-1\right],$$

(18)

where W(x) is the Lambert W function. Note that γ^* < 0, which means an inverse Gaussian function acts on the s-PQD of the measurement operator. From the fact that $\mathop{\max }\nolimits_{{\beta }_{j}}\left\vert {f}_{j}({\beta }_{j},{{{\Pi }}}_{1},{s}_{\max },{\gamma }^{* })\right\vert < 1$, the modified negativity bound ${{{{\mathcal{M}}}}}_{\to }^{{\prime} }$ is exponentially small in M for any squeezing r, which renders an efficient approximation with additive-error ϵ within running time $T=\,{{\mbox{poly}}}\,(M,1/\epsilon ,\log {\delta }^{-1})$.

Fig. 1: Schemes of quantum-inspired algorithms for approximating matrix functions.

For a given matrix function, a find an embedding of the matrix function onto an outcome probability of a quantum circuit (ρ, U, Π) and choose a quasiprobability representation of the probability. b We depict an example of a linear optical circuit, for the approximation scheme with additive-error. Using s-PQDs for the linear optical circuit, one can significantly reduce the negativity bound by appropriately choosing γ < 0. c Approximation scheme with multiplicative error. When the classicality of the input state is large, one can make the s-PQDs of the measurement operator a log-concave function by choosing a suitable ${\gamma }^{{\prime} } \,>\, 0$.

Furthermore, our method provides a stronger approximation scheme with multiplicative-error (see Fig. 1c). For instance, we consider an M-mode identical squeezed thermal state (r, n_th) having high enough classicality ${s}_{\max } > 1$ and all single-photon outcomes m = (1, …, 1). In this case, an appropriate γ > 0 can make s-PQD of the measurement operator a log-concave function by adding Gaussian smoothing.

Quantum-inspired algorithms for matrix functions

Permanent and hafnian are important matrix functions in computational complexity. Although computing these matrix functions is generally hard^21,33,34,35, there are still efficient methods for matrices that have specific structures or restrictions^24,25,36,37. Developing algorithms for estimating matrix functions of particular classes of matrices is a highly nontrivial problem and might enable us to understand the hardness of the problem better.

One approach is using quasiprobability representations of matrix functions. In general, there can be several ways to match the matrix functions with the outcome probability of quantum circuits (Fig. 1a). For example, an outcome probability of a linear optical circuit with photon number measurements and a Gaussian input state with zero-displacement having covariance matrix V can be written using a hafnian as²⁰

$$p({{{\boldsymbol{m}}}})=\frac{\,{{\mbox{Haf}}}\,({A}_{S})}{{{{\boldsymbol{m}}}}!\sqrt{| {V}_{Q}| }},$$

(19)

where ${V}_{Q}=V+{{\mathbb{I}}}_{2M}/2,A=\left(\begin{array}{cc}0&{{\mathbb{I}}}_{M}\\ {{\mathbb{I}}}_{M}&0\end{array}\right)\left({{\mathbb{I}}}_{2M}-{V}_{Q}^{-1}\right)$ and A_S is a submatrix of A with repeated rows and columns depending on the detected photons. Meanwhile, if the measurements are threshold detectors, i.e., ${{{\Pi }}}_{{{{\rm{off}}}}}=\left\vert 0\right\rangle \left\langle 0\right\vert$ and ${{{\Pi }}}_{{{{\rm{on}}}}}={\mathbb{1}}-\left\vert 0\right\rangle \left\langle 0\right\vert$, the corresponding probability is given in terms of Torontonian as³⁸

$$p({{{{\boldsymbol{m}}}}}^{{\prime} })=\frac{1}{\sqrt{| {V}_{Q}| }}\,{{\mbox{Tor}}}\,({O}_{S}),$$

(20)

where $O={{\mathbb{I}}}_{2M}-{V}_{Q}^{-1}$ and ${{{{\boldsymbol{m}}}}}^{{\prime} }$ is an M-element binary vector representing on/off measurement outcomes. Therefore, our approximating methods for an outcome probability p(m) are closely related to estimating the above matrix functions with additive- or multiplicative-errors.

Suppose we have a Gaussian input state as a squeezed thermal state. When the thermal part is absent, corresponding to the standard GBS circuit, we can obtain an algorithm for estimating the absolute square of the hafnian of a complex symmetric matrix:

Theorem 1

(Estimating hafnian) For an M × M complex symmetric matrix R, one can approximate ∣Haf(R)∣² with a success probability 1 − δ using the number of samples $O(\log {\delta }^{-1}/{\epsilon }^{2})$ within the additive-error

$$\epsilon {\left(\frac{{\lambda }_{\max }}{\sqrt{1-2W(1/e)}}\right)}^{M}\simeq \epsilon {(1.502{\lambda }_{\max })}^{M},$$

(21)

where ${\lambda }_{\max }$ is the largest singular value of R.

Proof

First, we embed the hafnian of a complex symmetric matrix to an outcome probability of a GBS circuit after rescaling the matrix so that its singular values are on the interval $\left[0,1\right)$. More specifically, when the input is an M-mode product of pure squeezed states with the squeezing parameters ${\{{r}_{i}\}}_{i = 1}^{M}$, the probability of a GBS circuit with all single-photon outcome m = (1, …, 1) is ${p}_{{{{\rm{sq}}}}}=\frac{1}{{{{\mathcal{Z}}}}}{\left\vert {{\mbox{Haf}}}(R)\right\vert }^{2}$ with ${{{\mathcal{Z}}}}=\mathop{\prod }\nolimits_{i = 1}^{M}\cosh {r}_{i},R=UD{U}^{T}$, and $D={\oplus }_{i = 1}^{M}\tanh {r}_{i}$²⁰. Since any complex symmetric matrix can be decomposed as UDU^T39 with a unitary matrix U, our algorithm can be applied to general complex symmetric matrices. Meanwhile, this probability can be also written by using s-PQDs in the form of Eq. (14) such as

$$\begin{array}{l}{p}_{{{{\rm{sq}}}}}\,=\,\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}\mathop{\prod }\limits_{i=1}^{M}\frac{1}{{{{{\mathcal{N}}}}}_{i}^{{{{\rm{sq}}}}}}{W}_{{V}_{{{{\rm{sq}}}},i}}^{(s)}({\alpha }_{i}){e}^{\gamma | {\alpha }_{i}{| }^{2}}\\ \quad\quad\, \times \,\mathop{\prod }\limits_{j=1}^{M}{{{{\mathcal{N}}}}}_{j}^{{{{\rm{sq}}}}}\frac{8| {\beta }_{j}{| }^{2}+2({s}^{2}-1)}{{(s+1)}^{3}}{e}^{-\left(\frac{2}{s+1}+\gamma \right)| {\beta }_{j}{| }^{2}}\\ \quad\quad\,:= \,\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}\mathop{\prod }\limits_{i=1}^{M}{P}_{{{{\rm{sq}}}},i}({\alpha }_{i},{r}_{i},s,\gamma )\mathop{\prod }\limits_{j=1}^{M}{f}_{{{{\rm{sq}}}},j}({\beta }_{j},{r}_{j},s,\gamma )\end{array}$$

(22)

where V_sq,i is the covariance matrix of the squeezed state on the ith mode and ${{{{\mathcal{N}}}}}_{i}^{{{{\rm{sq}}}}}$’s are the normalization factors for P_sq,i(α_i, r_i, s, γ)’s. Note that $\gamma \in (-\frac{2}{s+1},\frac{2}{{e}^{2{r}_{\max }}-s})$ for a given s and ${r}_{\max }:= \mathop{\max }\limits_{i}{r}_{i}$. An appropriate choice of γ (see Supplementary Note 1) gives an upper bound on ∣f_sq,j(β_j, r_j, γ, s)∣:

$$\begin{array}{rc}\left\vert {f}_{{{{\rm{sq}}}},j}({\beta }_{j},{r}_{j},\gamma ,s)\right\vert \,\le\, \frac{{\lambda }_{\max }^{2}\sqrt{1-{\lambda }_{j}^{2}}}{\sqrt{{\lambda }_{\max }^{2}{(1-W(1/e))}^{2}-{\lambda }_{j}^{2}W{(1/e)}^{2}}},\end{array}$$

(23)

where ${\lambda }_{j}=\tanh {r}_{j}$, and ${\lambda }_{\max }:= \mathop{\max }\nolimits_{j}{\lambda }_{j}$. Then by Hoeffding inequality⁴⁰,

$$\,{{\mbox{Pr}}}(| | {{\mbox{Haf}}}\,(R){| }^{2}-{{{\mathcal{Z}}}}\mu | \ge {{{\mathcal{Z}}}}\epsilon )\le 2\exp \left(-\frac{N{\epsilon }^{2}}{2{C}^{2M}}\right),$$

(24)

where ${{{\mathcal{Z}}}}=\mathop{\prod }\nolimits_{i = 1}^{M}1/\sqrt{1-{\lambda }_{i}}$ and $C=\mathop{\max }\nolimits_{j}| {f}_{{{{\rm{sq}}}},j}({\beta }_{j},{r}_{j},\gamma ,s)|$. Given the success probability of the estimation 1 − δ and the number of samples $O(\log {\delta }^{-1}/{\epsilon }^{2})$, we arrive at the result by substituting ${\lambda }_{j}={\lambda }_{\max }$ to obtain an upper bound. □

Note that the above algorithm gives the finest precision, to the best of our knowledge, i.e., $\epsilon {(e{\lambda }_{\max })}^{M}$ in Ref. ⁴¹. However, the error is still larger than what we need for the hardness conjecture in GBS⁴², so it does not lead to a contradiction. Next, if the input of the GBS circuit is a thermal state, we have an algorithm for the permanent of an HPSD matrix:

Theorem 2

(Estimating permanent of HPSD matrices) For an M × M HPSD matrix B, one can approximate Per(B) with a success probability 1 − δ using the number of samples $O(\log {\delta }^{-1}/{\epsilon }^{2})$ within the error

$$\epsilon \mathop{\prod }\limits_{i=1}^{M}\frac{4{\lambda }_{\max }^{2}}{e(2{\lambda }_{\max }-{\lambda }_{i})},$$

(25)

where λ_i are singular values of the matrix B and ${\lambda }_{\max }$ is the largest one.

Proof

This corresponds to the case where the input is an M-mode product of thermal states with the average photon numbers ${\{{n}_{i}\}}_{i = 1}^{M}$. The probability of all single-photon outcomes matches the permanent of an HPSD matrix B such as ${p}_{{{{\rm{th}}}}}=\frac{1}{{{{{\mathcal{Z}}}}}^{{\prime} }}\,{{\mbox{Per}}}\,(B),$ where ${{{{\mathcal{Z}}}}}^{{\prime} }=\mathop{\prod }\nolimits_{i = 1}^{M}(1+{n}_{i}),B=UD{U}^{{\dagger} }$, and $D=\,{{\mbox{diag}}}\,\{\frac{{n}_{1}}{{n}_{1}+1},\ldots ,\frac{{n}_{M}}{{n}_{M}+1}\}$. Then we obtain the result by a similar procedure in the hafnian case. A detailed derivation is given in Supplementary Note 1. □

The precision of our result outperforms the best-known one²³ because the latter is a special case of ours when s = 1 and γ = 0 (see Fig. 1b). Specifically, when ${\lambda }_{\max }\in (0,1/2)$, our method’s precision is better than the previous one (see Supplementary Note 1). Moreover, when the input is a squeezed thermal state, we obtain an algorithm for the hafnian of a structured matrix. Similarly, we provide algorithms for the Torontonian of some structured matrices within additive-error by substituting the photon number measurement with a threshold detector. The detailed results are in Supplementary Note 1.

Recall that we have an FPRAS when the estimate function is log-concave. Thus our goal is to make the estimate function log-concave by controlling the parameters s and γ in our scheme. For the permanent of an HPSD matrix, this is possible when ${\lambda }_{\max }/{\lambda }_{\min }\le 2$ (a proof in Supplementary Note 2), which reproduces the existing result of ref. ²⁶ in the case 1 ≤ λ_i ≤ 2 after a normalization. Especially for an HPSD matrix with ${\lambda }_{\min }=0$, estimating the permanent within a multiplicative-error is NP-hard⁴³; thus λ_i > 0 is the crucial condition for the efficient approximation. We emphasize that our formulation comes from a physical setup, which is essentially different from the method in ref. ²⁶, where the technique is restricted to the properties of the permanent of a positive definite matrix. Thus our result can be readily extended to a more general situation other than the permanent of a positive definite matrix. When the input state is a product of squeezed thermal states ${\{{r}_{i},{n}_{i}\}}_{i = 1}^{M}$, we have an FPRAS for the hafnian of a matrix having a specific form, such that 2 × 2 block matrix whose diagonal elements are symmetric matrices and off-diagonal elements are HPSD matrices.

Theorem 3

(FPRAS for hafnian) Suppose we have a block matrix $A=\left(\begin{array}{cc}R&B\\ {B}^{T}&{R}^{* }\end{array}\right)$ with an M × M complex symmetric matrix R and an M × M HPSD matrix B, which have decompositions by a unitary matrix U as UDU^T and $U{D}^{{\prime} }{U}^{{\dagger} }$, respectively, with

$$D=\mathop{\bigoplus }\limits_{i=1}^{M}\frac{(1+2n)\sinh 2{r}_{i}}{1+2n(1+n)+(1+2n)\cosh 2{r}_{i}},$$

(26)

$${D}^{{\prime} }=\mathop{\bigoplus }\limits_{i=1}^{M}\frac{2n(1+n)}{1+2n(1+n)+(1+2n)\cosh 2{r}_{i}},$$

(27)

where n = n_i for all i and n, r_i ≥ 0. Then Haf(A) can be approximated by FPRAS when the parameters satisfy a condition as

$$n\ge \frac{1}{4}\left(6\sinh (2{r}_{\max })+\sqrt{18\cosh (4{r}_{\max })-14}-2\right),$$

(28)

where ${r}_{\max }=\mathop{\max }\nolimits_{i}{r}_{i}$.

Proof

See Supplementary Note 2. □

We also consider an on/off measurement instead of the photon number measurement, which corresponds to the Torontonian (detailed analysis is given in Supplementary Note 2).

Moreover, we give nontrivial lower and upper bounds on the values of various matrix functions including the permanent and hafnian by adjusting the parameter s, which have independent interests (Supplementary Note 3)⁴⁴.

Sparse GBS

Our algorithm has an interesting application to the simulation of GBS. Recall that if the input is a classical state, the corresponding GBS can be efficiently simulated¹⁶. In our language, this is the case when ${s}_{\max }\ge 1$. For a non-classical input state (${s}_{\max } < 1$), however, a classically efficient simulation may not be possible from the hardness of GBS. Nevertheless, we can approximate any (marginal) outcome probability of the circuit using our algorithm under certain conditions. Then one can simulate the GBS when its output distribution is poly-sparse, in which a probability distribution with polynomially many of the most likely outcomes well approximates the true distribution^45,46.

Theorem 4

(Estimating outcome probabilities of GBS) For a lossy GBS circuit with squeezing ${\{{r}_{i}\}}_{i = 1}^{M}$ and a transmissivity η, one can efficiently approximate any (marginal) outcome probability within 1/poly(M) additive-error when $\eta {e}^{-2{r}_{\max }}+1-\eta \ge \sqrt{5}-2$ with ${r}_{\max }=\mathop{\max }\nolimits_{i}{r}_{i}$.

Proof

Let us first consider a GBS circuit with a product of lossy squeezed input states with a transmissivity η having the covariance matrix on ith mode as ${V}_{\eta ,i}=\frac{1}{2}\left(\begin{array}{cc}\eta {e}^{2{r}_{i}}+1-\eta &0\\ 0&\eta {e}^{-2{r}_{i}}+1-\eta \end{array}\right)$ and a photon number measurement ${{{\Pi }}}_{{m}_{j}}=\left\vert {m}_{j}\right\rangle \left\langle {m}_{j}\right\vert$. Then an outcome probability of m = (m₁, . . . , m_M) is given by

$$\begin{array}{rc}p({{{\boldsymbol{m}}}})\,=\,{\pi }^{M}\displaystyle\int{d}^{2M}{{{\boldsymbol{\alpha }}}}\mathop{\prod }\limits_{i=1}^{M}{W}_{{V}_{\eta ,i}}^{(s)}({\alpha }_{i})\mathop{\prod }\limits_{j=1}^{M}{W}_{{{{\Pi }}}_{{m}_{j}}}^{(-s)}({\beta }_{j}).\end{array}$$

(29)

We take $s={s}_{\max }=\eta {e}^{-2{r}_{\max }}+1-\eta$. If we examine the probability of all single-photon outcomes m = (1, …, 1), a condition for an efficient estimation is $\mathop{\max }\nolimits_{{\beta }_{j}}| \pi {W}_{{{{\Pi }}}_{1}}^{(-{s}_{\max })}({\beta }_{j})| \le 1$, which leads the restriction ${s}_{\max }\ge \sqrt{5}-2$. Now we must check whether this condition is valid for other outcomes. From the behavior of ${W}_{{{{\Pi }}}_{m}}^{(-s)}(\beta )$, we can find out that

$$\mathop{\max }\limits_{\beta }| {W}_{{{{\Pi }}}_{m}}^{(-s)}(\beta )| \le \mathop{\max }\limits_{\beta }| {W}_{{{{\Pi }}}_{1}}^{(-s)}(\beta )| ,$$

(30)

for n ≥ 2 and s ≥ 0. Lastly, we consider $\pi {W}_{{{{\Pi }}}_{0}}^{(-s)}({\beta }_{j})$ for zero-photon detection and ${\sum }_{{m}_{j}}\pi {W}_{{{{\Pi }}}_{{m}_{j}}}^{(-s)}({\beta }_{j})$ for the marginalized probability on mode j, where the latter sum equals to one by the normalization condition. In both cases, the integrals for β_j’s can be easily computed because β_j components in ${W}_{{V}_{\eta }}^{(s)}({{{\boldsymbol{\alpha }}}})$ constitute a multivariate normal distribution. Therefore, we can first perform the integrals on β_j’s corresponding to zero-photon or marginalized ones and estimate the remaining terms. □

Note that the condition in Theorem 4 yields ${r}_{\max }\le \frac{1}{2}\log (2+\sqrt{5})\simeq 0.722$ for an ideal GBS (η = 1). However, under photon loss, any squeezed input state is possible when $\eta \le 3-\sqrt{5}\simeq 0.764$, which is much higher transmissivity than those used in current experiments^12,13.

We also consider GBS with threshold detectors³⁸, whose s-PQD for “click” is given by

$$\pi {W}_{{{{\rm{on}}}}}^{(-s)}(\beta )=1-\frac{2}{s+1}{e}^{-\frac{2}{s+1}| \beta {| }^{2}}.$$

(31)

Since the range of $\pi {W}_{{{{\rm{on}}}}}^{(0)}(\beta )=1-2{e}^{2| \beta {| }^{2}}$ is [ − 1, 1] in the Wigner representation (s = 0), it allows any squeezing of the input state even for the lossless case (η = 1). Then we can estimate any (marginal) probability by the same argument of the photon-number measurement case. We give a detailed analysis in Supplementary Note 4.

In both cases, those algorithms of estimating (marginal) probability with inverse-polynomial additive-error precision with the poly-sparsity condition imply classically efficient simulations of GBS. Since it is difficult to expect the sparsity condition for current experiments, our results do not lead to a direct simulation of them. However, it can be useful for application-targeted GBS experiments whose outcomes might satisfy the poly-sparsity condition.

Furthermore, we might consider an additional source of noise to allow ${s}_{\max } > 1$ by introducing thermal noise with the average photon number n_th. In that case, the covariance matrix of ith mode input state is ${V}_{\eta ,{n}_{{{{\rm{th}}}}},i}=\frac{1}{2}\left(\begin{array}{cc}\eta {e}^{2{r}_{i}}+(1-\eta )(2{n}_{{{{\rm{th}}}}}+1)&0\\ 0&\eta {e}^{-2{r}_{i}}+(1-\eta )(2{n}_{{{{\rm{th}}}}}+1)\end{array}\right)$. By the log concavity condition, we can compute any (marginal) probability within a multiplicative-error if the following condition is satisfied:

$${n}_{{{{\rm{th}}}}}\ge \frac{{e}^{-{r}_{\max }}\eta \sinh {r}_{\max }+\sqrt{1+\eta \sinh 2{r}_{\max }}}{1-\eta } > 1.$$

(32)

For instance, if η = 0.5 and ${r}_{\max }=1$, then ${n}_{{{{\rm{th}}}}}\ge {n}_{{{{\rm{th}}}}}^{* }\simeq 3.79$, and the minimum value of ${n}_{{{{\rm{th}}}}}^{* }$ is 1 when η → 0.

In Fig. 2, we depict our results of approximating probability and simulation for GBS circuits with threshold detectors via the classicality ${s}_{\max }$. Remarkably, there are two transition points of complexities via the classicality ${s}_{\max }$. (i) ${s}_{\max }=1$: This point indicates the transition from ϵ-simulation with the sparse condition to exact simulation. Whether ϵ-simulation without sparse condition can exist when ${s}_{\max } < 1$ is an interesting open question. (ii) ${s}_{\max }={s}_{{{{\rm{m}}}}}$: Note that s_m is the point saturating the inequality Eq. (32), which indicates the transition of complexities from BPP^NP to BPP for approximating the probability within a multiplicative error.

Fig. 2: Complexity diagram of GBS circuit.

Regime of efficient classical algorithms for approximating outcome probabilities and the simulation of a GBS circuit with threshold detectors via the classicality ${s}_{\max }$. When the output distribution is poly-sparse, an approximate simulation is possible by estimating the probabilities within 1/poly additive-error (orange arrow)⁴⁵. On the other hand, a multiplicative-error approximation of probability in BPP^NP is possible by using exact simulation with classical input state ${s}_{\max }\ge 1$ (blue arrow)¹⁵.

Discussion

We propose a method for calculating the outcome probability of a linear optical circuit, by introducing modified functions with a lower negativity bound than the quasiprobability distribution. This leads to various improved approximating algorithms for the outcome probabilities of the circuit. Furthermore, we suggest an FPRAS using our method modulating s-PQDs and the efficient sampling of log-concave functions with multiplicative-error. Our results provide a helpful tool for controlling the negativity of the circuit in the phase space and interesting quantum-inspired algorithms in computational complexity.

Although we focus on Gaussian input states and photon number or threshold measurements in a linear optical circuit in this work, our scheme can be also applied to other systems, for example, Clifford circuits⁴⁷ with a dimension of odd prime d. If one exploits the symmetry of the transition function in the phase space, a nontrivial approximation algorithm can be rendered for the corresponding matrix function. Since there can be several equivalent choices of circuits for the same matrix function, e.g., permanent of a unitary matrix^48,49, finding the optimal circuit is still an interesting open problem. After a proper circuit choice, there are other optimization problems, such as choosing quasiprobability representation and optimizing parameters for manipulating them in the phase space. Therefore, there might be more improvements for quantum-inspired algorithms for approximating corresponding matrix functions.