Resolving Fock states near the Kerr-free point of a superconducting resonator

Abstract

We have designed a tunable nonlinear resonator terminated by a SNAIL (Superconducting Nonlinear Asymmetric Inductive eLement). Such a device possesses a Kerr-free point in which the external magnetic flux allows to suppress the Kerr interaction. We have excited photons near this Kerr-free point and characterized the device using a transmon qubit. The excitation spectrum of the qubit allows to observe photon-number-dependent frequency shifts about nine times larger than the qubit linewidth. Our study demonstrates a compact integrated platform for continuous-variable quantum processing that combines large couplings, considerable relaxation times and excellent control over the photon mode structure in the microwave domain.

Introduction

Encoding quantum information in the infinite Hilbert space of a harmonic oscillator is a promising avenue for quantum computing. Recently, significant progress has been made by using three-dimensional (3D) microwave cavities^{1,2,3,4,5,6,7}. Thanks to the strong-dispersive coupling, quantum states such as cat states^8,9, GKP states¹⁰ and the cubic phase state¹¹ have been engineered. However, currently, the scalability and connectivity is difficult, limited by the size of the cavity. Another simpler method is to use coplanar microwave resonators where resonators and qubits can be fabricated together in a single chip^12,13,14. The drawback is the shorter relaxation time of coplanar resonators compared to 3D cavities.

Both 2D and 3D microwave resonators as well as acoustic resonators^15,16 host linear modes. Therefore, an ancillary qubit is customarily used to introduce nonlinearity for state preparation and operation. However, the limited coherence of the ancillary qubit and the imperfect operations on it will decrease the fidelity of the actual states^11,17,18. To avoid operations on ancillary qubits, a Superconducting QUantum Interference Device (SQUID) can be used to terminate a coplanar resonator. This not only provides the tunability of the mode frequency by changing the external magnetic flux through the loop^{19,20,21,22,23,24}, it also induces sufficient nonlinearity. Using this nonlinearity, experiments in waveguide quantum electrodynamics have demonstrated the generation of entangled microwave photons by the parametrical pumping of a symmetrical SQUID loop^25,26. Non-Gaussian states, regarded as a resource for quantum computing, have also been realized^27,28,29. Therefore, state preparation and operations can be implemented in a nonlinear resonator with a nonlinearity about 0.3%, much weaker than in a typical transmon qubit (~4%). However, in those experiments, the generated states can not be stored for a long time since the resonators are directly coupled to the waveguides.

Theoretically, it has been shown that pulsed operations on a novel tunable nonlinear resonator can be used to achieve a universal gate set for continuous-variable (CV) quantum computation³⁰. The proposed device is similar to a parametric amplifier where the Josephson junction or SQUID loop is replaced by an asymmetric Josephson device known as the SNAIL (Superconducting Nonlinear Asymmetric Inductive eLement)^31,32, is applied. Using a SNAIL or an asymmetrically threaded SQUID loop^33,34, it is possible to realize three-wave mixing free of residual Kerr interactions by biasing the element at a certain external magnetic flux. In this work, we refer to this flux spot as the Kerr-free point.

Therefore, it is meaningful to investigate a SNAIL-terminated resonator in circuit quantum electrodynamics (cQED) where the nonlinear resonator, decoupled from the waveguide, can be used for state preparation and storage. Strong dispersive coupling between oscillators and qubits was achieved a decade ago for photons¹² and recently for phonons^35,36,37, in linear resonators. Here, we observed the very well-resolved photon-number splitting up to the 9th-photon Fock state in a SNAIL-terminated resonator coupled to a qubit. Our nonlinear resonator has a considerable relaxation time up to T₁ = 8 μs at the single-photon level, intrinsically limited by Two-Level Systems (TLSs). Our study opens the door to implementing, operating and storing quantum states on this scalable platform in the future. Moreover, compared to a linear resonator, our resonator has a non-negligible dephasing rate from its high sensitivity to the magnetic flux noise due to the SNAIL loop.

Results

Characterization of the SNAIL-terminated resonator

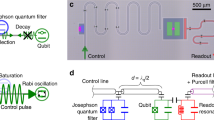
To characterize the parameters for the SNAIL-terminated resonator directly, we first fabricated a SNAIL-terminated λ/4 resonator capacitively coupled to a coplanar transmission line [not shown], which is similar to the nonlinear resonator shown (in blue) in Fig. 1. By measuring the transmission coefficient through a vector network analyzer similar to measuring conventional resonators^38,39,40,41, at the 10 mK stage of a dilution refrigerator, we can extract the nonlinear resonator frequency at different external magnetic fluxes [see Methods]. For our SNAIL-terminated resonator, the inductive energy can be written as^30,31,32

$${U}_{{{{\rm{SNAIL}}}}}(\phi )=-\beta {E}_{{{{\rm{J}}}}}\cos (\phi )-3{E}_{{{{\rm{J}}}}}\cos \left(\frac{{\phi }_{{{{\rm{ext}}}}}-\phi }{3}\right),$$

(1)

where β is the ratio of the Josephson energies of the small and the big junctions of the SNAIL, ϕ is the superconducting phase across the small junction, ϕ_ext = 2πΦ_ext/Φ₀ is the reduced external magnetic flux, and E_J, related to the Josephson inductance L_J, is the Josephson energy of the big junctions in the SNAIL. Upon quantization, the Hamiltonian for the SNAIL-terminated resonator becomes

$${H}_{{{{\rm{s}}}}}=\hslash {\omega }_{{{{\rm{s}}}}}{a}^{{\dagger} }a+{g}_{3}{(a+{a}^{{\dagger} })}^{3}+{g}_{4}{(a+{a}^{{\dagger} })}^{4},$$

(2)

where g₃ (g₄) is the three (four)-wave mixing coupling strength, and ω_s is the frequency of the SNAIL-terminated resonator, which follows the relation³⁰

$${\omega }_{{{{\rm{s}}}}}\tan \left(\frac{\pi }{2}\frac{{\omega }_{{{{\rm{s}}}}}}{{\omega }_{{{{\rm{r}}}}0}}\right)=\frac{{Z}_{{{{\rm{r}}}}}{c}_{2}}{3{L}_{J}},$$

(3)

where ω_r0 describes the bare resonance frequency of the resonator without the SNAIL, Z_r = 58.7 Ω for the characteristic impedance of the resonator, and c₂ is a numerically determinable coefficient for the linear coupling whose specific value depends on β and ϕ_ext in our case.

Fig. 1: A scanning optical micrograph of the measured sample.

A superconducting qubit with a cross-shaped island (green) and a single Josephson junction (JJ, light blue in the middle inset), capacitively coupled to both a coplanar read-out resonator (red) and the nonlinear resonator (blue). The nonlinear resonator is formed by a linear coplanar resonator terminated by a superconducting nonlinear asymmetric inductive element (SNAIL) that has three big Josephson junctions and one small junction (orange in right inset). The charge line (pink) is used to operate the qubit and drive the nonlinear resonator. The qubit state read-out is implemented through the transmission of the feedline. The on-chip flux line is not used in this work, instead, a superconducting coil on the top of the chip [not shown] is used to generate the external magnect flux Φ_ext through the SNAIL. See more fabrication details and the measurement setup for this device in Methods. The lengths of scale bars for the figure and the inserts are 200 μm and 10 μm, respectively.

We measure the transmission coefficient which results from a very weak probe (the mean number of photons on the resonator due to the probe is smaller than one). From this measurement we extract the internal Q_s values at Φ_ext = 0 and Φ_ext = 0.386 Φ₀ close to the Kerr-free point, where the magnetic flux is calibrated using the flux period Φ₀ of the SNAIL-terminated resonator frequency. As shown in Table 1, we find that the coherence time in both cases is above one microsecond, especially, T_s ≈ 7 μs at Φ_ext = 0. When we tune the resonator to Φ_ext = 0.386 Φ₀, the coherence time is reduced by a factor of five due to the pure dephasing from the magnetic flux noise through the SNAIL.

Table 1 SNAIL-terminated resonator parameters at zero magnetic flux and near the Kerr-free point.

A SNAIL-terminated resonator coupled to a qubit

In order to verify the nonlinear resonator performance in cQED in Fig. 1, the nonlinear resonator is dispersively coupled to a fixed-frequency superconducting qubit [shown in green in Fig. 1] with the bare qubit frequency ω_q0/2π ≈ 5.222 GHz [see more details on estimating this value in Methods]. The effective Hamiltonian that contains the leading order corrections to the rotating wave approximation for describing the coupled SNAIL-terminated resonator and qubit in the dispersive regime (g₀ ≪ Δ₀)⁴² is

$$\frac{{H}_{{{{\rm{eff}}}}}}{\hslash }\approx {\omega }_{{{{\rm{c}}}}}{a}^{{\dagger} }a+K{a}^{{\dagger} 2}{a}^{2}+{\omega }_{{{{\rm{q}}}}}{b}^{{\dagger} }b-\frac{{\chi }_{0}}{2}{a}^{{\dagger} }a{b}^{{\dagger} }b-\frac{{\alpha }_{q}}{2}{b}^{{\dagger} 2}{b}^{2},$$

(4)

where the bare SNAIL-terminated resonator is dispersively shifted to ${\omega }_{{{{\rm{c}}}}}={\omega }_{{{{\rm{s}}}}}-{g}_{0}^{2}/{{{\Delta }}}_{0}$, and similarly, the bare frequency ω_q0 of the qubit mode b is dispersively shifted to ${\omega }_{{{{\rm{q}}}}}={\omega }_{{{{\rm{q0}}}}}+{g}_{0}^{2}/{{{\Delta }}}_{0}$ with g₀ the coupling strength between the nonlinear resonator and the qubit, and Δ₀ = ω_q0 − ω_s the detuning between the resonator and the bare qubit frequencies. The dispersive shift is ${\chi }_{0}=\frac{{g}_{0}^{2}{\alpha }_{{{{\rm{q}}}}}}{{{{\Delta }}}_{0}({{{\Delta }}}_{0}-{\alpha }_{{{{\rm{q}}}}})}$ with the qubit anharmonicity α_q/2π ≈ 450 MHz. Furthermore, near the Kerr-free point where the Kerr nonlinearity (strength K) is cancelled in the leading order, the residual Kerr nonlinearity is due to the interplay of four- and three-wave mixing processes³⁰ as well as the qubit-induced nonlinearity.

To experimentally find the qubit frequency, we sweep the frequency of a qubit-excitation pulse with the pulse length τ_p = 1 μs (spectroscopy pulse, see the pulse generation in Methods). When the nonlinear resonator frequency is changed by the external flux Φ_ext, the values of Δ₀ and the qubit frequency are also changed. In Fig. 2a, at a fixed Φ_ext, we sweep the pulse frequency, and when the pulse is on resonance with the qubit, the qubit is excited. Then, we measure the qubit state by sending a readout pulse to obtain S(ρ_ee) ∝ ρ_ee, which is manifested as bright dots in Fig. 2a. After finding the qubit frequency and calibrating the corresponding π-pulses at different values of Φ_ext, we send a continuous coherent drive to the nonlinear resonator while driving the qubit on resonance. However, when the drive is on resonance with the nonlinear resonator, the resonator is populated, leading to a change of the qubit frequency due to the dispersive interaction. Thus, the π-pulse will not excite the qubit anymore, resulting in a smaller signal S(ρ_ee) (Fig. 2b).

Fig. 2: Spectroscopy for the qubit frequency and the SNAIL-terminated resonator frequency.

a The qubit frequency vs. the external magnetic flux through the SNAIL. b The SNAIL-terminated resonator frequency vs. the external magnetic flux through the SNAIL. The nonlinear resonator is dispersively coupled to the qubit as shown in Fig. 1. S(ρ_ee) ∝ ρ_ee is the measured signal from the read-out pulse of the qubit. ω_p is the probe frequency.

With the values of ω_q0 and the dressed-qubit frequencies, we can obtain the values of the Stark shift at different external magnetic fluxes. Therefore, we can compensate the Stark shift from the qubit onto the SNAIL-terminated resonator to obtain the bare resonator frequency ω_s [blue dots in Fig. 3a from Fig. 2b]. With the parameters extracted from Fig. 3a, we can calculate the Kerr coefficient as a function of external magnetic flux [pink curve in Fig. 3b]. Moreover, at the device operation point Φ_ext = 0.386 Φ₀ [green dot in Fig. 3b], close to the Kerr-free point Φ_ext = 0.392 Φ₀, we estimate the residual Kerr interaction strength K/2π = − 310 ± 40 kHz with g₃/2π = − 11.6 ± 0.4 MHz, and g₄/2π = − 0.128 ± 0.004 MHz, where the residual Kerr nonlinearity is still mainly from the nonlinearity of the SNAIL.

Fig. 3: Frequency and Kerr strength for SNAIL-terminated resonator coupled to a qubit.

a The frequency of the nonlinear resonator vs. the external magnetic flux through the SNAIL. Blue dots (red curve) are (is) the experimental (fitting) data. By fitting the data to Eq. (3) [red curve], we obtain β = 0.09993 ± 0.00005, well matched with the resistance ratio of the big junction over the small junction 0.104, measured at room temperature, L_J = 629 ± 8 pH and ω_r0/2π = 8.87 ± 0.07 GHz. The crossed point from two blacklines indicate the corresponding resonator frequency at the Kerr-free point. b The Kerr-frequency shift per photon, K, vs. the external magnetic flux through the SNAIL calculated from the parameters in (a). The crossed point from two black lines indicates that the Kerr coefficient is zero at Φ_ext = 0.392 Φ₀. The green dot at Φ_ext = 0.386 Φ₀ is the operating flux point in our work.

Due to the dispersive coupling to the qubit, the qubit can be used as a very efficient probe to determine the frequency of the SNAIL-terminated resonator. In our case, the external coupling strength between the nonlinear resonator and charge line is only γ_c/2π = 2.07 kHz. Thus, it will be extremely difficult to find the resonator frequency based on the reflection coefficient measurement^43,44,45,46 through the charge line. However, since our qubit is coupled to the resonator with a dispersive shift up to a few MHz as shown in Fig. 5b, a few photons inside the resonator will shift the qubit frequency significantly. Consequently, even though the frequency detuning between the probe frequency and the resonator frequency is much larger than the instrinsic linewidth of the resonator, as soon as the intensity of the probe is strong enough to inject a few photons inside the resonator, we can perform qubit spectroscopy to roughly find the resonator frequency. Afterwards, we can find the resonator frequency more accurately by decreasing the probe intensity (Fig. 4a).

Fig. 4: The spectroscopy of the nonlinear resonator near the Kerr-free point with different probe powers.

a The signal S(ρ_ee) is from the readout pulse, depending on the qubit population ρ_ee where ρ_ee is determined by the nonlinear resonator photon population. ω_p is the frequency of the continuous probe where we vary the probe power to the sample from −142 dBm to −124 dBm. The dip indicates the resonator frequency. Each experimental spectroscopy (dots) is fitted to a Gaussian function (solid curves) to obtain the resonator frequencies and the linewidths at different probe powers. At the lowest probe power, we find that the qubit-dressed resonator frequency is ω_c/2π ≈ 4.296 GHz. b The frequency shift, Δω_c = ω_c,n − ω_c, is obtained from the fittings in (a), where ω_c,n is the resonator frequency with the average photon number n in the resonator. Due to the residual Kerr effect, we obtain K/2π = − 236 ± 65 kHz by fitting the data to a linear function according to Δω_c = K〈n〉. The average photon number is estimated from probe powers according to Eq. (5). c The linewidth of the dip is reduced from about 1.5 MHz to 0.3 MHz, where the linewidth is fitted to a function $\xi \sqrt{\langle n\rangle }+{\gamma }_{{{{\rm{s}}}}}$⁴⁷, with a parameter ξ related to K and the value of γ_s/2π = 112 kHz from Table 1.

We estimate the photon number according to the relation

$$\langle n\rangle =2\frac{{Z}_{{{{\rm{c}}}}}}{{Z}_{{{{\rm{r}}}}}}\frac{{Q}_{l}^{2}}{{Q}_{{{{\rm{c}}}}}}\frac{P}{\hslash {\omega }_{{{{\rm{c}}}}}^{2}},$$

(5)

where we have the charge-line impedance Z_c = 46 Ω, the loaded quality factor of the resonator Q_l ≈ Q_s = 3.86 × 10⁴, the external quality factor Q_c = 2.08 × 10⁶ from the numerical simulation, and the probe power P. Due to the residual Kerr coefficient, the spectroscopy is therefore of Gaussian shape from the photon-number fluctuation in the resonator⁴⁷. Thus, we can extract both the resonator frequency shift and the linewidth with the estimated photon number, as shown in Fig. 4b and c with the residual Kerr coefficient K/2π = − 236 ± 65 kHz, agreeing well with the value extracted from Fig. 3b.

Photon-number splitting near the Kerr-free point

Once we have determined the nonlinear resonator frequency, we perform a pump-probe measurement consisting of a short pulse (50 ns) to excite the resonator followed by a qubit excitation with τ_p = 2 μs, Rabi frequency Ω/2π = 250 kHz while sweeping the probe frequency ω_p, along with a read-out pulse at the end to infer the qubit excited-state population. Due to the weak hybridization between the qubit and the nonlinear resonator near the Kerr-free point, the short coherent pulse drives the resonator into an approximate coherent state with amplitude ∣α∣. We observed the qubit frequency splitting with the Fock states up to 9 photons where each peak has a Gaussian shape due to the quantum fluctuation of the photon number inside the resonator⁴⁷ [Fig. 5a]. The separation of each peak is about 3 MHz, ten times larger than the qubit linewidth $\frac{{\gamma }_{{{{\rm{q}}}}}}{2\pi }\approx 280\,{{{\rm{kHz}}}}$, leading to well-resolved peaks, where the qubit linewidth is mainly dominated by the Rabi-broadening. The pulse length satisfies τ_p ≫ 1/γ_q, resulting in a good frequency resolution.

Fig. 5: Photon-number splitting and lifetime of the SNAIL-terminated resonator near the Kerr-free point.

a Normalized transmitted readout signal S(ω_q) where the envelope is the qubit-frequency distribution P(ω_q), satisfying $1/2\pi \int\nolimits_{0}^{\infty }P({\omega }_{{{{\rm{q}}}}})\,d{\omega }_{{{{\rm{q}}}}}=1$, with the average photon number ∣α∣² ≈ 6, of the coherent displacement in the nonlinear resonator. The envelope of the distribution matches well with a Poisson distribution with the corresponding coherent-state amplitude ∣α∣ ≈ 2.4 [red solid line]. b Dispersive shift χ over different photon numbers n inside the nonlinear resonator. The data is fitted to the equation $\chi ={\chi }_{0}+{\chi }^{{\prime} }(n-1)/2$ with χ₀/2π = 3.143 ± 0.021 MHz and the higher order correction ${\chi }^{{\prime} }/2\pi =35\pm 11\,{{{\rm{kHz}}}}$. c the qubit population ρ_ee depending on the photon number 〈n〉 = ∣α∣² in the nonlinear resonator. τ is the waiting time after the short displacement before the qubit read-out. d The relaxation time T₁ of the nonlinear resonator vs. different photon number 〈n〉 inside the resonator. The error bars are for the standard deviation.

From the peak difference of the qubit spectroscopy, we can extract the dispersive shift which increases with the photon number shown in Fig. 5b [see Methods]. The coupling strength g₀/2π ≈ 53 MHz follows from the dispersive shift χ₀ and the qubit anharmonicity α_q. Moreover, near the Kerr-free point, the self-Kerr K_sq of the SNAIL-resonator induced by the qubit-resonator coupling^42,48 is ${K}_{{{{\rm{sq}}}}}=-24{g}_{4}{g}_{0}^{2}/{{{\Delta }}}_{0}^{2}\approx -2\pi \times 9\,{{{\rm{kHz}}}}$, which is more than three hundred times smaller than the dispersive shift and more than 10 times smaller than γ_s. Thus, the residual Kerr coefficient from the qubit has a small influence on the states stored in our device, which can be also completely suppressed by slightly shifting the external flux Φ_ext.

Lifetime of a single photon in the nonlinear resonator near the Kerr-free point

Even though a statistical study can be done by measuring multiple resonators coupled to waveguides to infer the average lifetime, it is still important to study the relaxation time directly on a specific device in cQED since in reality the device performance varies over different devices due to the imperfect fabrication process.

Here, for the device shown in Fig. 1, utilizing the dispersive coupling to the qubit, we can determine the energy lifetime of the nonlinear resonator T₁ at the single-photon level. Again, we send a 50 ns pulse to displace the resonator with the initial amplitude ∣α(τ = 0)∣, and after a time delay τ, we apply a conditional π-pulse where the frequency is equal to the qubit frequency when the resonator is empty. In the experiment, the spectral width of the excitation pulse is σ/2π ≈ 80 kHz, more than one order of magnitude smaller than the dispersive shift χ, making the pulse selectivity $1-\exp (\frac{-{\chi }^{2}}{2{\sigma }^{2}})\, >\, 0.999$⁴⁹. Therefore, the qubit-excitation population strongly depends on the photon number 〈n〉. In Fig. 5c at τ ~ 0, when 〈n〉 < 1, the qubit frequency is still mainly centered at ω_q/2π = 5.228 GHz, leading to the qubit population ρ_ee ≈ 1. However, when 〈n〉 > 1, the qubit frequency starts to split, leading to a decreased ρ_ee where the population goes to zero smoothly and reaches ρ_ee ≈ 0 with 〈n〉 = 5.8. However, with increasing τ, the coherent field in the resonator decreases as $\alpha (\tau )=\alpha (0)\exp (-\tau /(2{T}_{1}))$ and the qubit frequency moves back. Thus, the conditional pulse can excite the qubit again.

Two-level systems (TLSs) are investigated extensively using conventional coplanar resonators^{39,50,51,52,53,54,55} along waveguides, where the photon number inside the resonator can be only roughly estimated according to the attenuation of the setup. Here, thanks to the accurate calibration of the photon number inside the nonlinear resonator, it is possible to directly study the effects of the TLSs on our nonlinear resonator. The value of T₁ in Fig. 5d, extracted from the data in Fig. 5c [see Methods], increases from 8 μs to 20 μs, which can be explained by saturation of two-level systems (TLS). According to the TLS model^52,55,56, the resonator internal Q₁ is given by

$$\frac{1}{{Q}_{1}}=\frac{1}{{\omega }_{{{{\rm{c}}}}}{T}_{1}}=F{\delta }_{{{{\rm{TLS}}}}}\frac{\tanh \left(\frac{\hslash {\omega }_{{{{\rm{c}}}}}}{2{k}_{{{{\rm{B}}}}}{T}_{{{{\rm{res}}}}}}\right)}{\sqrt{1+\frac{\langle n\rangle }{{n}_{{{{\rm{c}}}}}}}}+{\delta }_{{{{\rm{other}}}}},$$

(6)

where F is the filling factor describing the ratio of electrical field in the TLS host volume to the total volume. δ_TLS is the TLS loss tangent of the dielectric hosting the TLSs, n_c is the critical photon number within the resonator to saturate one TLS, and δ_other is the contribution from non-TLS loss mechanisms. A fit to Eq. (6) gives Fδ_TLS ≈ 4.5 × 10⁻⁶, δ_other ≈ 1.3 × 10⁻⁶ and n_c ≈ 0.1 photons [red solid curve in Fig. 5d], which is several orders of magnitude smaller than for normal linear resonators^{38,39,40,52,54,55,57}. Here, it is reasonable to consider that the TLSs are nearly resonant with the resonator, and therefore, they lead to its energy dissipation. Thus, the Rabi frequency induced by the resonator electrical field on the TLSs is ${{{\Omega }}}_{{{{\rm{TLS}}}}}={g}_{{{{\rm{TLS}}}}}\sqrt{\langle n\rangle }$ with a single-photon coupling strength g_TLS and the average number of photons 〈n〉 in the resonator. According to $\langle n\rangle /{n}_{{{{\rm{c}}}}}={{{\Omega }}}_{{{{\rm{TLS}}}}}^{2}{T}_{1,{{{\rm{TLS}}}}}{T}_{2,{{{\rm{TLS}}}}}$⁵⁶, with T_1,TLS and T_2,TLS as the average relaxation time and the decoherence time of the TLSs, respectively, we obtain

$$2{T}_{1,{{{\rm{TLS}}}}}^{2}\ge {T}_{1,{{{\rm{TLS}}}}}{T}_{2,{{{\rm{TLS}}}}}=\frac{1}{{g}_{{{{\rm{TLS}}}}}^{2}{n}_{{{{\rm{c}}}}}},$$

(7)

due to T_2,TLS ≤ 2T_1,TLS. Since there is no anti-crossing in the spectroscopy measurement on the resonator, it is very possible that the TLSs are distributed on the surface of the resonator instead of the junction barrier due to no strong coupling between our resonator and TLSs. Thus, according to the numerical simulation for the surface TLSs where in our case the maximal coupling strength is estimated as ${g}_{{{{\rm{TLS}}}}}^{\max }/2\pi =222\,{{{\rm{kHz}}}}$, we obtain T_1,TLS ≥ 1.60 μs [See Methods]. In addition, we also analyse the non-TLS loss where the loss could be possible from both the circuit design and chip modes [See Methods].

Compared to the coherence time of the SNAIL-terminated resonator coupled to a waveguide near the Kerr-free point, the relaxation time here is significantly larger, indicating that the coherence time is limited by the pure dephasing. Assuming that the resonator coupled to the waveguide has the same internal relaxation time as the nonlinear resonator coupled to a qubit, according to 1/T_s = 1/(2T₁) + 1/T_ϕ with T₁ ≈ 8 μs at 〈n〉 ≈ 0 from Fig. 5d, we can infer the pure dephasing time T_ϕ ≈ 12 μs and 2 μs at Φ_ext = 0 and Φ_ext = 0.386 Φ₀, respectively. Especially, at Φ_ext = 0.386 Φ₀, the resonator becomes much more sensitive to the magnetic flux noise, leading to a shorter coherence time which could be increased by reducing the SNAIL parameter β or adding more magnetic shielding to suppress the magnetic-flux noise or decrease the loop size.

Discussion

In this study, we developed an efficient method to characterize a SNAIL-terminated nonlinear resonator and observed well-resolved photon-number splitting up to nine photons, where the relaxation time can be up to 8 μs, limited by the TLSs. It is important to demonstrate the possibility to reach the strong dispersive regime necessary for the resonator readout at the Kerr-free point.

The parameters of our device are suitable for implementing universal gate sets for quantum computing³⁰ [See Methods]. Compared to linear modes coupled to qubits, in our case, the Kerr effect from the ancilla qubit can be suppressed, leading to better storage of bosonic modes where the Kerr coefficient makes the quantum state collapse⁴⁹. In order to estimate the capability of storing bosonic states for quantum information in our nonlinear resonator, the maximal coherent state which can be stored in the resonator is limited by the cavity critical photon number ${n}_{{{{\rm{c}}}}}\equiv {({{{\Delta }}}_{0}/g)}^{2}/4\approx 77$ with the pure dephasing time roughly given by T_ϕ/〈n〉² [See Methods]. Due to a limited value of T_ϕ ≈ 2 μs for our current device, in the future, the main problem is to reduce the pure dephasing rate of the resonator to improve the coherence time of the bosonic states stored in our system. Moreover, by taking the advantage of the nonlinearity of our resonator, we could also generate and store non-Gaussian entanglement in different modes²⁸. The dispersive coupling between the qubit and the resonator could also enable us to make quantum state tomography very efficiently. Finally, compared to 3D cavities, our chip-scale structure is more compact for integration and scalability required by the large-scale CV quantum processing in the future.

Methods

Experimental setup

The complete experimental setup is shown in Fig. 6. The sample, as shown in Fig. 1, is wire-bonded in a nonmagnetic oxygen-free cooper sample box, mounted to the 10 mK stage of a dilution refrigerator, and shielded by a μ-metal can which is used for suppressing the static and fluctuating magnetic field. The signal to the qubit and the SNAIL-terminated resonator, with heavy attenuation, is combined to the charge line on the sample. A pulse is sent to the feedline on the sample to read out the state of the qubit with amplification using a traveling-wave parametric amplifier (TWPA) at the 10 mK stage, a high electron mobility transistor (HEMT) amplifier at 3 K and a room-temperature amplifier.

Fig. 6: Experimental setup.

Complete wiring diagram and room temperature setup for the nonlinear resonator coupled to a qubit. The qubit operation and the pulsed displacement are made by analog upconversion of the pulsed generated by an AWG (blue and orange). The dashed line in the blue box means that sometimes the microwave generator is connected to the combiner to pump the resonator continuously. The qubit readout (yellow) is controlled by the up- and down-conversion of a pulse generated by an AWG, and then digitized by an analog to digital converter (ADC).

Sample fabrication

We first clean a high-resistance (10 kΩ) 2-inch silicon wafer by using hydrofluoric acid with 2% concentration. Then, we evaporate aluminum on top of the silicon substrate, followed by direct laser writing, and etching using wet chemistry to obtain all the sample details except the Josephson junction. The Josephson junctions for the qubit and the SNAIL are defined in a bi-layer resist stack using electron-beam lithography. Later, we deposit aluminum again by using a two-angle evaporation technique. In order to ensure a superconducting contact between the junctions and the rest of circuit, an argon ion mill is used to remove native aluminium oxide before the junction aluminium deposition. Finally, the wafer is diced into individual chips and cleaned properly using both wet and dry chemistry.

Device parameters for the SNAIL-terminated resonator coupled to the waveguide

By sending a microwave probe to the SNAIL-terminated resonator coupled to the waveguide [the device used for Table 1], we measure the transmission coefficient of a SNAIL-terminated resonator to obtain the bare resonator frequency [blue stars in Fig. 7a]. Then, we get β = 0.095 and ${E}_{{{{\rm{J}}}}}/(2\pi \hslash )=\frac{\hslash }{4{e}^{2}{L}_{{{{\rm{J}}}}}}\approx 830\,{{{\rm{GHz}}}}$ with the Josephson inductance L_J = 600 pH by fitting the data to Eq. (3) [solid curve]. In Fig. 7b, based on the values of E_J and β, we numerically calculate the Kerr coefficient K due to the four-wave mixing coupling, in which K can be suppressed to zero at the flux point Φ_ext/Φ₀ = 0.39. When we tune the SNAIL-terminated resonator to the minima frequency by the external magnetic flux, the frequency detuning between the qubit and the resonator is maximized, large enough to obtain Δ₀ = ω_q0 − ω_s ≈ ω_q − ω_s ≈ 2π × 1.211 GHz with ω_q/2π ≈ 5.227 GHz and ω_s/2π = 4.016 GHz. With the value of α_q/2π ≈ 450 MHz and χ₀/2π = 3.143 MHz, we therefore obtain $\frac{{g}_{0}^{2}}{{{{\Delta }}}_{0}}=\frac{{\chi }_{0}({{{\Delta }}}_{0}-{\alpha }_{{{{\rm{q}}}}})}{{\alpha }_{{{{\rm{q}}}}}}\approx 2\pi \times 5.35\,{{{\rm{MHz}}}}$. Thus, we have the bare qubit frequency ${\omega }_{{{{\rm{q0}}}}}={\omega }_{{{{\rm{q}}}}}-{g}_{0}^{2}/{{{\Delta }}}_{0}\approx 2\pi \times 5.222\,{{{\rm{GHz}}}}$.

Fig. 7: Frequency and Kerr strength for a SNAIL-terminated resonator coupled to a waveguide.

a The frequency of the nonlinear resonator vs. the external magnetic flux through the SNAIL. Stars are the experimental data determined from the transmission coefficient of the vector network analyzer. The solid blue curve is calculated numerically. b The Kerr-frequency shift per photon, K, vs. the external magnetic flux through the SNAIL. The Kerr-free point occurs at Φ_ext = 0.39 Φ₀.

Pulse generation and calibration

The microwave control for the qubit and the nonlinear resonator is achieved by up-converting the in-phase (I) and the quadrature (Q) components of a low-frequency pulse generated by four AWG channels (two each for the qubit and the resonator). The qubit read-out pulse is up-converted to the sample and then down-converted after the amplification with the same local oscillator (yellow area). The pump pulse for the displacement is generated by an IQ mixer with an input pulse from an Arbitrary Waveform Generator (AWG) with amplitude. In Fig. 8, we vary the amplitude of the pump pulse by changing the voltage amplitude A, and then obtain the corresponding displacement in the resonator according to the photon-number splitting. The data (black dots) is fitted to the equation ∣α∣ = kA with k ≈ 8. This measurement is useful to calibrate the pump pulse with different amplitudes. We also notice that the residual thermal population with A = 0 is ∣α∣ = 0.16 (〈n〉 = ∣α∣² ≈ 0.03 photons). The thermal and Poisson distributions are almost the same when the thermal photon number is small. In this case, we only take into account the single photon P₁ and the vacuum P₀ populations.Thus, we can calculate the corresponding thermal temperature as ${T}_{{{{\rm{res}}}}}=\hslash {\omega }_{{{{\rm{c}}}}}/\left[{k}_{{{{\rm{B}}}}}\ln \left(1+\frac{1}{\langle n\rangle }\right)\right]\approx 58\,{{{\rm{mK}}}}$.

Fig. 8: Pulse amplitude calibration.

Calibration of the coherent displacement α with the voltage output A, of the arbitrary-wavefunction generator at the room-temperature.

Kerr coefficient estimation

According the extracted parameters β and L_J from Fig. 3a, we can calculate the coefficients g₃ and g₄ for the three-wave mixing and four-wave mixing terms, respectively (Fig. 9). Then, we can infer the coupling strength for the Kerr coefficient K according to $K=12({g}_{4}-5{g}_{3}^{2}/{\omega }_{{{{\rm{s}}}}})$, as shown in Fig. 3b.

Fig. 9: g₃ and g₄ numerical values for the SNAIL-terminated resonator coupled to a qubit.

The numerical values of g₃ from a and g₄ from b for the SNAIL-terminated resonator coupled to a qubit.

Qubit spectroscopy

In order to increase the signal-to-noise ratio, here, we average the qubit spectroscopy with different resonator-frequency driven voltages from Fig. 10a to obtain Fig. 10b. Afterwards, each peak corresponding to a specific photon number is fitted to a Gaussian function to extract the dispersive shift as shown in Fig. 5b.

Fig. 10: Qubit spectroscopy under different resonator-frequency drive voltages.

a Normalized transmitted readout signal S(ω_q) Vs. different drive voltages. b The averaged qubit-frequency distribution.

The lifetime T ₁ of the resonator

In Fig. 11, The data trace [black stars] is from the top trace in Fig. 5c with the average photon number 〈n〉 = 5.8. Here, we show an example to obtain the value of T₁ from Fig. 5c. The qubit excitation probability is ${\rho }_{{{{\rm{ee}}}}}=\exp [-| \alpha (0){| }^{2}\exp (-\tau /{T}_{1})]$. By fitting the rising curve (Fig. 11) with the calibrated $| \alpha (0)| =\sqrt{5.8}\,$(〈n〉 = 5.8), we extract T₁ = 19.2 ± 0.2 μs, corresponding to a quality factor of Q₁ = ω_cT₁ ≈ 5.18 × 10⁵ which is close to the Q₁ value for a coplanar linear resonator in the few-photon limit^40,57.

Fig. 11: Extract the value of T₁ from the qubit population.

The qubit population ρ_ee vs. the waiting time τ with 〈n〉 = 5.8.

Estimation on the value of g _TLS

The capacitance of the SNAIL-terminated resonator is from the bare resonator. Therefore, according to ${\omega }_{{{{\rm{r0}}}}}/2\pi =\frac{1}{\sqrt{{L}_{l}{C}_{l}}}\frac{1}{4l}=\frac{1}{4\sqrt{{L}_{{{{\rm{r0}}}}}{C}_{{{{\rm{r0}}}}}}}$ where L_l, C_l and l are the inductance per length, the capacitance per length and the length of the resonator with L_r0 = L_l × l and C_r0 = C_l × l, we obtain ${C}_{{{{\rm{r0}}}}}=\frac{\pi }{2{\omega }_{{{{\rm{r0}}}}}{Z}_{{{{\rm{r}}}}}}$ with ${Z}_{{{{\rm{r}}}}}=\sqrt{\frac{{L}_{{{{\rm{r0}}}}}}{{C}_{{{{\rm{r0}}}}}}}$. The root mean square of the resonator electric field is given by⁵⁸:

$${E}_{{{{\rm{s}}}}}^{{{{\rm{rms}}}}}=\frac{{U}_{{{{\rm{s}}}}}^{{{{\rm{rms}}}}}}{{t}_{{{{\rm{gap}}}}}}=\frac{1}{{t}_{{{{\rm{gap}}}}}}\sqrt{\frac{1}{{T}_{{{{\rm{osc}}}}}}\int\nolimits_{0}^{{T}_{{{{\rm{osc}}}}}}{U}_{{{{\rm{s}}}}}{(t)}^{2}dt}$$

(8)

$$=\frac{1}{{t}_{{{{\rm{gap}}}}}}\sqrt{\frac{\hslash {\omega }_{{{{\rm{s}}}}}}{2{C}_{{{{\rm{r0}}}}}}}=\frac{1}{{t}_{{{{\rm{gap}}}}}}\sqrt{\frac{\hslash {\omega }_{{{{\rm{s}}}}}{\omega }_{{{{\rm{r0}}}}}{Z}_{{{{\rm{r}}}}}}{\pi }},$$

(9)

where T_osc is the oscillation time period and ${U}_{{{{\rm{s}}}}}(t)=\sqrt{\hslash {\omega }_{{{{\rm{s}}}}}/{C}_{{{{\rm{r0}}}}}}\sin ({\omega }_{{{{\rm{s}}}}}t)$. For our resonator with a gap width of t_gap = 12 μm, we have ${U}_{{{{\rm{s}}}}}^{{{{\rm{rms}}}}}\approx 1.72\,{{{\rm{\mu V}}}}$ with ${E}_{{{{\rm{s}}}}}^{{{{\rm{rms}}}}}\approx 0.14\,{{{\rm{V/m}}}}$. In order to obtain the boundary of the value of g_TLS, we perform a numerical simulation with COMSOL. The result in Fig. 12 shows that the electric field is concentrated around the edge of the resonator with the maximal available numerical value of ${E}_{{{{\rm{q}}}}}^{\max }=23\,{{{\rm{V/m}}}}$ at the bottom corner. Therefore, according to the dipole moment of TLSs with d = 0.2 − 0.4 eÅ⁵⁸, we can estimate the maximum value of ${g}_{{{{\rm{TLS}}}}}^{\max }/2\pi =222\,{{{\rm{kHz}}}}$.

Fig. 12: Electric field distribution from the single-photon excitation on the SNAIL-terminated resonator.

The black dot from the numerical simulation is the electric field E over the distance r, starting from bottom corner of the resonator towards the ground plane indicated by the red arrow in the inset. The data is fitted to a function of E = h/r^d with h = 4.76 and d = 0.42 (red curve), where the fit indicates the polynomial decay law of the field strength^51,58,59. Inset: the numerical simulation on the electric field by COMSOL. AlO_x and SiO_x denote the oxidized layers on the top of resonator and the silicon substrate, respectively. In the simulation, for the oxidized layer, the maximum (minimum) mesh size is 0.02 (0.015) nm. For the Aluminum electrode, the maximum mesh size is 0.1 nm with the minimum size 0.02 nm.

The losses of the nonlinear resonator

In order to improve T₁ further in the future, we also analyse the non-TLS loss. The non-TLS loss limits the lifetime to be T_other = 1/(δ_otherω_c) ≈ 28 μs comparable to our qubit lifetime T_1,q ≈ 20 μs. In our sample, the nonlinear resonator couples to the qubit, charge line and a flux line where they contribute to the non-TLS loss as ${\gamma }_{{{{\rm{q}}}}}/2\pi ={({g}_{0}/{{{\Delta }}}_{0})}^{2}\frac{1}{{T}_{1,{{{\rm{q}}}}}}\approx 170\,{{{\rm{Hz}}}}$, γ_c/2π ≈ 2.07 kHz and γ_f/2π ≈ 477 Hz, respectively (the values of γ_c and γ_f are from the simulation). In total, the loss from the chip design is γ_total = γ_q + γ_c + γ_f ≈ 2π × 2.717 kHz corresponding to T_total = 1/γ_total ≈ 59 μs ≈ 2T_other, meaning that other unknown losses such as the chip modes are similar to the loss from the chip design.

Coherent states in the resonator

The current in the resonator should be much smaller than the critical current of the Josephson junctions of the SNAIL in order to make the element linear. Here we take the currents through the junctions 10 times smaller than the critical currents (I = 0.1I_c). According to I_c = Φ₀/(2πL_J) with L_J = 629 pH, we obtain I_small,c ≈ 52 nA and I_big,c ≈ 520 nA for the small and big junctions, respectively. Therefore, the energy of the big (small) Josephson junction is E_big,J = L_JI²/2 ≈ 9 × 10⁻²⁵ J (E_small,J ≈ 9 × 10⁻²⁶ J). Meanwhile, the linear inductance of the bare resonator is L_r0 = πZ_r/2ω_r0 ≈ 1.63 nH, leading to an inductive energy ${E}_{{{{\rm{r0}}}}}={L}_{{{{\rm{r0}}}}}{({I}_{{{{\rm{big,c}}}}}+{I}_{{{{\rm{small,c}}}}})}^{2}/2\approx 3.0\times 1{0}^{-22}\,{{{\rm{J}}}}$. Thus, the corresponding photon number is (E_r0 + E_small,J + 3E_big,J)/ℏω_c ≈ 107 with ℏω_c ≈ 2.8 × 10⁻²⁴ J. Meanwhile, it is also important to avoid to excite the qubit, therefore, the photon number should be much smaller than the cavity critical photon number ${n}_{{{{\rm{c}}}}}\equiv {({{{\Delta }}}_{0}/g)}^{2}/4\approx 77$⁴⁷. In summary, the current device has a limited maximal photon number that can be stored due to the dispersive coupling to the qubit.

Moreover, since our nonlinear resonator mainly suffers the pure dephasing, at the Kerr-free point in the rotating frame of the resonator frequency, we estimate the dephasing rate for a coherent state according to the Lindblad master equation,

$$\frac{d\rho }{dt}=2{\kappa }_{\phi }{a}^{{\dagger} }a\rho {a}^{{\dagger} }a-{\kappa }_{\phi }[{({a}^{{\dagger} }a)}^{2}\rho +\rho {({a}^{{\dagger} }a)}^{2}],$$

(10)

where ρ is the density matrix of the state in the resonator, and κ_ϕ = 1/T_ϕ is the instrinc pure dephasing rate. Therefore, we can obtain $\frac{d{\rho }_{nm}}{dt}=-{\kappa }_{\phi }{(n-m)}^{2}{\rho }_{nm}$, where n and m indicate the photon number in the Fock space. Considering that the photon-number variation of a coherent state is 〈n〉, the pure phasing rate is therefore about κ_ϕ〈n〉² = 〈n〉²/T_ϕ.

Summary of sample parameters for the cubic-phase state

Our device is possible for implementing some non-Gaussian states for the continuous-variable quantum computing. For implementing the cubic phase state which is the key element for the universal quantum set for the continuous-variable quantum computing, the required device parameters are summarized in Table 2. Based on these parameters, we numerically obtain a cubic phase state with a fidelity up to 93% in Fig. 13a. (See more details on the simulation in ref. ³⁰.)

Table 2 Device parameters required for the cubic phase state, where the values are extracted in experiments.

Fig. 13: Numerical cubic phase state.

a The numerical cubic phase state based on the parameters from Table 2. b The ideal cubic phase state.