Strong majorization uncertainty relations and experimental verifications

Abstract

In spite of enormous theoretical and experimental progress in quantum uncertainty relations, the experimental investigation of the most current, and universal formalism of uncertainty relations, namely majorization uncertainty relations (MURs), has not been implemented yet. A major problem is that previous studies of majorization uncertainty relations mainly focus on their mathematical expressions, leaving the physical interpretation of these different forms unexplored. To address this problem, we employ a guessing game formalism to reveal physical differences between diverse forms of majorization uncertainty relations. Furthermore, we tighter the bounds of MURs by using flatness processes. Finally, we experimentally verify strong MURs in the photonic system to benchmark our theoretical results.

Introduction

In the quantum world, measurements allow us to gain information from a system, and the action of measurements on quantum systems is fully embraced in the areas of quantum technologies and quantum information theories. It is therefore of great practical interest to study the limitations and precisions of quantum measurements. In taking the measurements on board, however, it appears that quantum mechanics imposes strict limitation on our ability to specify the precise outcomes from incompatible measurements simultaneously, which is known as Heisenberg uncertainty principle¹.

In the context of the uncertainty principle, both variance^{2,3,4,5,6,7,8,9,10,11,12} and entropies^{13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45} are by no reason the most adequate to use. The attempt to find all suitable uncertainty measures has triggered the interest of the scientific community in the quest for a better understanding and exploitation of the precisions of quantum measurements. As previously shown in refs. ^46,47, any eligible candidate of uncertainty measures should be: (i) non-negative; (ii) a function only of the probability vector associated with the measurement outcomes; (iii) invariant under permutations; (iv) nondecreasing under a random relabeling(characterized by the convex hull of permutation matrices). According to these restrict conditions, a qualified uncertainty measure should be a non-negative Schur-concave function, and the majorization uncertainty relations (MURs) arise from the fact that all Schur-concave functions preserve the partial order induced by majorization^48,49,50. Based on the mathematical expressions, the notions of MURs are classified into two categories; that are direct-product MUR (DPMUR)^46,51 and direct-sum MUR (DSMUR)^52,53. In the original work⁵², the essential differences of mathematical features between DPMUR and DSMUR (i.e. tensor and direct-sum) are compared and analyzed. However, it is fair to say, that our understanding of the physical essences of MURs is still very limited.

In this work, our first contribution, which also reflects the original intention of this work, is to characterize the essential differences of physical features between DPMUR and DSMUR theoretically. More precisely, we show that the difference between these MURs are more than its mathematical expressions, what really matters is the joint uncertainty they represent. DPMUR is identified as a type of spatially-separated joint uncertainty, and meanwhile DSMUR is recognized as a type of temporally-separated joint uncertainty. Despite previous developments on MURs, there is still a gap between their optimal bounds and the ones constructed in refs. ^46,51,52,53. Our second contribution is to fill this gap by applying a technique, called the flatness process⁵⁴, which is also known as a concave envelope in mathematics.

Besides theoretical advancements, the experimentally implementations of quantum uncertainty relations are also already of great interest. Uncertainty relations based on variance and entropies have been successfully realized in various physical systems, including neutronic systems^55,56,57, optical systems^{22,23,58,59,60,61,62,63,64}, nitrogen-vacancy centers⁶⁵, nuclear magnetic resonance⁶⁶, ion trap⁶⁷, and so forth. However, an experimental demonstration of the uncertainty relations given by majorization has never been shown. To boost the experimental study of the uncertainty relations, we experimentally verified the tighter majorization uncertainty relations. Thus the third contribution of this work is that we demonstrate the MURs by measuring a qudit state encoded with the path and polarization degrees of freedom of the photon.

Results

Direct-product majorization uncertainty relation

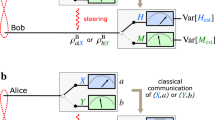
We employ guessing games to reveal physical differences between diverse forms of majorization uncertainty relations. The guessing game for the construction of DPMUR is shown in Fig. 1a. In each round of the game, Bob prepares a two-copy state ρ ⊗ ρ and sends it to Alice(the state is unknown to Alice). Alice measures the state ρ ⊗ ρ with M ⊗ N (the measurement is known to Bob), and M, N is positive-operator-valued measures (POVMs) composed of m POVM elements and n POVM elements, denoted as $M={\{{M}_{a}\}}_{a}$(a = 1, …, n) and $N={\{{N}_{b}\}}_{b}$ (b = 1, …, m) respectively. Then Alice obtains a measurement outcome labeled as (a, b), which has mn possible results, as shown in the table in Fig. 1a, where a denotes the outcome of M and b denotes the outcome of N. Alice obtains a measurement outcome (a, b) in each round, and Bob’s goal is to guess Alice’s measurement outcome correctly in each round. Each round is independent, and only the number of measurement outcomes that Bob is allowed to guess increases in each round.

Fig. 1: Schematic illustration of the majorization uncertainty relations in the framework of guessing games.

The guessing game for the construction of DPMUR is shown in (a). Bob prepares a two-copy state ρ ⊗ ρ which is unknown to Alice and sends it to Alice. Alice measures the state ρ ⊗ ρ with M ⊗ N and obtains a measurement outcome (a, b) with a = 1, …, n and b = 1, …, m. The state and measurements are known to Bob, so Bob knows that Alice’s measurement outcome in each round is one of the mn possible outcomes. Bob’s goal is to guess Alice’s measurement outcome correctly in each round. Each round is independent and the process is the same, except that Bob is allowed to guess the number of measurement outcomes increasing in each round. For example, in the second round(k = 2), Bob is allowed to guess two outcomes out of all possible outcomes(as shown in blue in the table) and will win if one of them is Alice’s measurement outcome. The guessing game for the construction of DSMUR is shown in (b). Unlike the game for DPMUR, in this game, Bob prepares a one-copy state ρ and sends it to Alice. Alice measures the state ρ using either M or N depending on the outcome of a random number generator R, which outputs 0 with probability λ and 1 with probability 1 − λ. Thus Alice obtains a measurement outcome (0, a) or (1, b) in each round. Bob knows Alice’s measurement rules and his goal is to guess Alice’s measurement outcome correctly among n + m possible outcomes. Similarly, in the k-th round, Bob is allowed to guess k outcomes out of all possible outcomes and will win if one of them is Alice’s measurement outcome.

In the first round of the game, Bob is allowed to guess only one possible measurement outcome, and he will win if he guesses correctly. In the k-th round of the game, Bob is allowed to guess k possible measurement outcomes, he will win if one of his guesses is Alice’s measurement outcome. It can be seen that this game can play up to k = nm rounds. It is important to highlight that Bob possesses information about the state and measurements Alice will implement during the game. Therefore, Bob has prior information on the possible measurement outcomes and can directly guess the measurement outcome that occurs with the maximum probability. Moreover, since Bob is the party sending the states, he can maximize the probability of winning in each round by sending the particular states. For example, in the first round, the maximum probability for Bob to win is ${\max }_{\rho }{p}_{a}{q}_{b}$, where the probabilities p_a and p_b are written as ${p}_{a}:= {{{\rm{Tr}}}}\left({M}_{a}\,\rho \right)$ and ${q}_{b}:= {{{\rm{Tr}}}}\left({N}_{b}\,\rho \right)$. In the second round, according to the rules, Bob is allowed to guess two outcomes simultaneously and will win if one of his guesses is Alice’s measurement outcome. He chooses the two outcomes that occur with the maximum sum of probabilities among all possible outcomes. So the maximum probability for Bob to win in the second round is $\mathop{\max }\limits_{{I}_{2}}\mathop{\max }\limits_{\rho }{\sum }_{\left(a,b\right)\in {I}_{2}}{p}_{a}{q}_{b}$, where I₂ represents the set composed of selecting two outcomes from mn possible measurement outcomes. Thus in the k-th round, the maximum probability for Bob to win can be expressed as

$${R}_{k}:= \mathop{\max }\limits_{{I}_{k}}\mathop{\max }\limits_{\rho }\mathop{\sum}\limits_{\left(a,b\right)\in {I}_{k}}{p}_{a}{q}_{b},$$

(1)

where I_k ⊂ [n] × [m] is a subset of k distinct pair of indices. Here [n] = {1, …, n} is the set of natural numbers ranging from 1 to n, and k ∈ [mn]. According to Eq. (1), it is easy to obtain the following inequalities

$$\mathop{\sum}\limits_{\left(a,b\right)\in {I}_{k}}{p}_{a}{q}_{b}\,\leqslant \,{R}_{k}.\quad \forall k\in [mn]$$

(2)

A concise approach of expressing the inequalities mentioned above is to use the majorization ( ≺ )⁵⁰; A probability vector ${{{\bf{x}}}}\in {{\mathbb{R}}}^{n}$ is majorizied by ${{{\bf{y}}}}\in {{\mathbb{R}}}^{n}$, i.e. x ≺ y, if and only if $\mathop{\sum }\nolimits_{j = 1}^{k}{x}_{j}^{\downarrow }\leqslant \mathop{\sum }\nolimits_{j = 1}^{k}{y}_{j}^{\downarrow }$ for all 1 ⩽ k ⩽ n − 1. Here the down-arrow indicates that the components of the vectors are arranged in a non-increasing order. We write the probability distributions p_a and p_b of all results for M and N as probability vectors p and q, respectively. Clearly, the joint uncertainty between p and q is captured by the maximum probability for Bob to win the game. Now we can abbreviate the Eq. (2) into one inequality

$${{{\bf{p}}}}\otimes {{{\bf{q}}}}\prec {{{\boldsymbol{r}}}},$$

(3)

with ${{{\boldsymbol{r}}}}:= \left({R}_{1},{R}_{2}-{R}_{1},\ldots ,{R}_{mn}-{R}_{mn-1}\right)$. Consequently, the essence of DPMUR is captured by our framework of guessing game, which demonstrates a spatially-separated joint uncertainty. Note that R_k can be in general difficult to calculate explicitly, as they involve an optimization problem. The authors of ref. ⁴⁶ provide us a calculate-friendly bound t, satisfying p ⊗ q ≺ r ≺ t. However, this is not the optimal bound. Mathematically, majorization lattice forms a complete lattice; the optimal bounds for MURs exist. To obtain the optimal bounds, it suffices to perform a standard process (flatness process) ${{{\mathcal{F}}}}$. Hence, the implementation of the process ${{{\mathcal{F}}}}$ on p ⊗ q ≺ r ≺ t lead to a relation

$${{{\bf{p}}}}\otimes {{{\bf{q}}}}\prec {{{\mathcal{F}}}}\left({{{\boldsymbol{r}}}}\right)\prec {{{\boldsymbol{r}}}}\prec {{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)\prec {{{\boldsymbol{t}}}},$$

(4)

where r and t are the bounds given in ref. ⁴⁶. Because of the mathematical properties of flatness process (concave envelope), the vector ${{{\mathcal{F}}}}\left({{{\boldsymbol{r}}}}\right)$ is optimal. However, a major drawback of ${{{\mathcal{F}}}}\left({{{\boldsymbol{r}}}}\right)$ is that the calculation of ${{{\mathcal{F}}}}\left({{{\boldsymbol{r}}}}\right)$ is even harder than r. But with the help of flatness process, we also obtain an effectively computable bound ${{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)$, which is tighter than the original t. So we obtain a strong DPMUR ${{{\bf{p}}}}\otimes {{{\bf{q}}}}\prec {{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)\prec {{{\boldsymbol{t}}}}$, and we test this relation experimentally. The construction of t and the rigorous definition of the flatness process see Supplementary Note 1 for details.

Direct-sum majorization uncertainty relation

Demonstration of direct-sum majorization uncertainty relation (DSMUR) through the framework of the guessing game is shown in Fig. 1b. In each round of the game, Bob prepares a one-copy state ρ and sends it to Alice(the state is unknown to Alice). Alice measures the state ρ with M or N. To determine Alice’s choice of the measurements, a binary random number generator R is employed, which outputs the number 0 with probability λ, and the number 1 with probability 1 − λ. After receiving 0 from R, Alice performs the measurement M and obtains a measurement outcome labeled as (0, a), where a ∈ {1, …, n}. Otherwise, she implements N and obtains a measurement outcome labeled as (1, b), where b ∈ {1, …, m}. n + m possible results {(0, a), (1, b)} are shown in the table in Fig. 1b. Thus Alice obtains a measurement outcome (0, a) or (1, b) in each round. Bob knows Alice’s measurement rules and the specific form of measurements M and N, but he does not know whether Alice performs measurement M or N in each round. So he needs to guess Alice’s outcome among all possible results.

Same as the previous game for DPMUR, again the goal of Bob is to guess Alice’s measurement outcome correctly in each round. Each round is independent, and the number of measurement outcomes that Bob is allowed to guess increases in each round. In the k-th round of the game, Bob is allowed to guess k possible measurement outcomes, and he will win if one of his guesses is Alice’s measurement outcome. This means that the game can be played up to k = n + m rounds. Bob’s strategy is similar to the previous one. Thus the maximal probability for Bob to win in each round is given by

$${S}_{k}:= \mathop{\max }\limits_{| I| +| J| =k}\mathop{\max }\limits_{\rho }\mathop{\sum}\limits_{\begin{array}{c}a\in I\subset [n]\\ b\in J\subset [m]\end{array}}\left(\lambda {p}_{a}+\left(1-\lambda \right){q}_{b}\right)$$

(5)

where ∣•∣ denotes the cardinality of •. There exists an efficient way of computing S_k. Let us define an operator G_c as

$${G}_{c}\left(\lambda \right):= \left\{\begin{array}{ll}\lambda {M}_{c}&1\,\leqslant\, c\,\leqslant\, n,\\ \left(1-\lambda \right){N}_{c-n}&n+1\,\leqslant \,c\,\leqslant \,n+m.\end{array}\right.$$

(6)

Then the quantity S_k becomes

$${S}_{k}\left(\lambda \right)=\mathop{\max }\limits_{| I| =k}{\lambda }_{1}\left(\mathop{\sum}\limits_{c\in I\subset [n+m]}{G}_{c}\left(\lambda \right)\right),$$

(7)

where ${\lambda }_{1}\left(\bullet \right)$ denotes the maximum eigenvalue of the argument. Similarly, we write the relationship between the uncertainty of measurements and Bob’s maximum probability of winning the game as the following inequality by using majorization

$$\lambda {{{\bf{p}}}}\oplus \left(1-\lambda \right){{{\bf{q}}}}\prec {{{\boldsymbol{s}}}}\left(\lambda \right),$$

(8)

with ${{{\boldsymbol{s}}}}\left(\lambda \right):= \left({S}_{1}\left(\lambda \right),{S}_{2}\left(\lambda \right)-{S}_{1}\left(\lambda \right),\ldots ,{S}_{m+n}\left(\lambda \right)-{S}_{m+n-1}\left(\lambda \right)\right)$. In the framework of DSMUR, classical uncertainty of the random number generator is injected into the guessing game, and as a consequence $\lambda {{{\bf{p}}}}\oplus \left(1-\lambda \right){{{\bf{q}}}}$ is a hybrid type of uncertainty, mingling both classical and quantum uncertainties. Quite remarkably, the measurements, monitored by R, can be implemented in the same position but cannot performed simultaneously, and hence $\lambda {{{\bf{p}}}}\oplus \left(1-\lambda \right){{{\bf{q}}}}$ reveals a temporally-separated joint uncertainty. It should be stressed here that the original DSMUR^52,53 is a special case of our notion by first taking λ = 1/2, and then timing the scalar 2, i.e. ${{{\bf{p}}}}\oplus {{{\bf{q}}}}\prec 2{{{\boldsymbol{s}}}}\left(1/2\right)$.

Let us now consider the DSMUR after flatness process

$$\lambda {{{\bf{p}}}}\oplus \left(1-\lambda \right){{{\bf{q}}}}\prec {{{\mathcal{F}}}}\left({{{\boldsymbol{s}}}}\left(\lambda \right)\right)\prec {{{\boldsymbol{s}}}}\left(\lambda \right).$$

(9)

Unlike the case of DPMUR, the vector ${{{\mathcal{F}}}}\left({{{\boldsymbol{s}}}}\left(\lambda \right)\right)$ is optimal and can be calculate explicitly. Moreover, for DSMUR with uniform distribution, i.e. λ = 1/2, one can easily show that ${{{\bf{p}}}}\oplus {{{\bf{q}}}}\prec 2{{{\mathcal{F}}}}\left({{{\boldsymbol{s}}}}\left(1/2\right)\right)\prec 2{{{\boldsymbol{s}}}}\left(1/2\right)$. Note that, the flatness process cannot be applied to ${{{\bf{p}}}}\oplus {{{\bf{q}}}}\prec 2{{{\boldsymbol{s}}}}\left(1/2\right)$ directly^40,41, since the results presented in ref. ⁵⁴ are only designed for probabilities. To accommodate this, a more general lemma is proved in Supplementary Note 3.

Experimental demonstration

To verify the DPMUR and DSMUR, we experimentally prepare a family of 4-dimensional states with parameters θ and ϕ, $\vert {\psi }_{\theta ,\phi }\rangle =\cos \theta \sin \phi \left\vert 0\right\rangle +\cos \theta \cos \phi \left\vert 1\right\rangle +\sin \theta \left\vert 2\right\rangle +0\left\vert 3\right\rangle$, and perform measurements in the photonic system. Measurements include a setting with a pair of measurements

$$\begin{array}{l}A=\left\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle ,\left\vert 2\right\rangle ,\left\vert 3\right\rangle \right\}\\ B=\begin{array}{l}\left\{\left(\left\vert 0\right\rangle -{{{\rm{i}}}}\left\vert 1\right\rangle -{{{\rm{i}}}}\left\vert 2\right\rangle +\left\vert 3\right\rangle \right)/2,\left(\left\vert 0\right\rangle -{{{\rm{i}}}}\left\vert 1\right\rangle +{{{\rm{i}}}}\left\vert 2\right\rangle -\left\vert 3\right\rangle \right)/2\right.,\\ \left.\left(\left\vert 0\right\rangle +{{{\rm{i}}}}\left\vert 1\right\rangle -{{{\rm{i}}}}\left\vert 2\right\rangle -\left\vert 3\right\rangle \right)/2,\left(\left\vert 0\right\rangle +{{{\rm{i}}}}\left\vert 1\right\rangle +{{{\rm{i}}}}\left\vert 2\right\rangle +\left\vert 3\right\rangle \right)/2\right\}\end{array}\end{array}$$

(10)

and another one with multi-measurements

$$\begin{array}{l}{C}_{1}=\left\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle ,\left\vert 2\right\rangle ,\left\vert 3\right\rangle \right\}\\ {C}_{2}=\left\{\left\vert 0\right\rangle ,\frac{\left\vert 2\right\rangle +\left\vert 3\right\rangle }{\sqrt{2}},\frac{\left\vert 1\right\rangle +\left\vert 2\right\rangle -\left\vert 3\right\rangle }{\sqrt{3}},\frac{2\left\vert 1\right\rangle -\left\vert 2\right\rangle +\left\vert 3\right\rangle }{\sqrt{6}}\right\}\\ {C}_{3}=\left\{\frac{\left\vert 2\right\rangle +\left\vert 3\right\rangle }{\sqrt{2}},\left\vert 1\right\rangle ,\frac{\left\vert 0\right\rangle +\left\vert 2\right\rangle -\left\vert 3\right\rangle }{\sqrt{3}},\frac{2\left\vert 0\right\rangle -\left\vert 2\right\rangle +\left\vert 3\right\rangle }{\sqrt{6}}\right\}.\end{array}$$

(11)

The experimental setup is shown in Fig. 2. It consists of a single-photon source module, a state-preparation module, and a measurement module. The details of each module are presented in the Methods section.

Fig. 2: Experimental setup.

In the single-photon source module, the photon pairs generated in spontaneous parametric down-conversion are coupled into single-mode fibers separately. One photon is detected by a single-photon detector (SPD) acting as a trigger. In the state preparation module, a qudit is encoded by four modes of the single photon. H and V denote the horizontal polarization and vertical polarization of the photon, respectively. The subscripts u and d represent the upper and lower spatial modes of the photon, respectively. The half-wave plates (H₁, H₂) and beam displacer (BD1) are used to generate desired qudit state. In the measurement module a, b, the red HWPs with an angle of 45° and beam displacers (BDs) comprise the interferometric network to perform the desired measurement; the yellow HWP with an angle of 0° are inserted into the middle path to compensate the optical path difference between the upper and lower spatial modes. To realize measurement B shown in Eq. (10), two quarter-wave plates are need to be inserted in device b. Four SPDs correspond to the four outcomes of each measurement. Each SPD is a silicon avalanche photodiode (Si-APD), with a detection efficiency of ~ 60%.

The probability distributions induced by performing measurements (10) and (11) on state $\left\vert {\psi }_{\theta ,\phi }\right\rangle$ are acquired. Since we need to verify the majorization relation between vectors composed of probability distributions, so we use Lorentz curve to show it more intuitively⁵⁰. For an non-negative vector ${{{\bf{x}}}}={\left({x}_{i}\right)}_{i = 1}^{n}$ with non-increasing order, the corresponding Lorenz curve ${{{\mathcal{L}}}}\left({{{\bf{x}}}}\right)$ is defined as the linear interpolation of the points $\{(k,\sum\nolimits_{i=1}^{k}x_{i})_{k=0}^{n}\}$ with the convention $\left(0,0\right)$ for k = 0. Based on Lorenz curves, we have ${{{\mathcal{L}}}}\left({{{\bf{x}}}}\right)$ lays everywhere below ${{{\mathcal{L}}}}\left({{{\bf{y}}}}\right)$ if and only if x ≺ y. Therefore, we convert the probability vectors p ⊗ q and p ⊕ q into Lorentz curves ${{{\mathcal{L}}}}\left({{{\bf{p}}}}\otimes {{{\bf{q}}}}\right)$ and ${{{\mathcal{L}}}}\left({{{\bf{p}}}}\oplus {{{\bf{q}}}}\right)$, and then compare them with the Lorentz curves of bounds of majorization uncertainty relations.

Experimental results for verifying the DPMUR and DSMUR with two measurements are shown in Fig. 3. Figure 3a, b show the Lorentz curves of probability vectors for DPMUR and DSMUR by measuring the states $\vert {\psi }_{\pi /4,\phi }\rangle$, respectively. Figure 3c, d show the Lorenz curves of probability vectors for DPMUR and DSMUR with states $\vert {\psi }_{\theta ,\pi /4}\rangle$, respectively. For measurements A and B, the bound t for DPMUR, introduced in refs. ^46,51, is given by $\left(0.5625,0.1661,0.2714\right)$. The corresponding Lorenz curve ${{{\mathcal{L}}}}\left({{{\bf{t}}}}\right)$ is shown as black curve in Fig. 3a, c. To further improve previous result on DPMUR, we apply the flatness process ${{{\mathcal{F}}}}$ to the bound t, and acquire a strong bound ${{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)=\left(0.5625,0.21875,0.21875\right)$. The corresponding Lorenz curve ${{{\mathcal{L}}}}\left({{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)\right)$ is shown as red curve in Fig. 3a, c. According to the rules of the flatness process, the second and third elements of t are not arranged in descending order, so the first element of ${{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)$ is still the first element of t, and the average of the second and third elements of t is taken as the second and third elements of ${{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)$. Similarly, the bound $2{{{\boldsymbol{s}}}}\left(1/2\right)$ for DSMUR, introduced in ref. ⁵², is given by $\left(0.5,0.2071,0.2929\right)$. After flatness process, the improved bound ${{{\mathcal{F}}}}\left({{{\boldsymbol{s}}}}\left(1/2\right)\right)=\left(0.5,0.25,0.25\right)$ is obtained. The Lorentz curve of improved bound is shown as a red curve, and as a comparison, the Lorentz curve of previous bound as a black curve in Fig. 3b, d. The experimental plots depicted in Fig. 3 confirm the betterments of our bounds by showing that all experimental datum-induced Lorenz curves lay below our bounds ${{{\mathcal{F}}}}\left({{{\boldsymbol{t}}}}\right)$ (${{{\mathcal{F}}}}\left({{{\boldsymbol{s}}}}\left(1/2\right)\right)$), and our bounds are under the previous ones t (${{{\boldsymbol{s}}}}\left(1/2\right)$), which implies that our bound is tighter.

Fig. 3: Experimental results of DPMUR and DSMUR with two measurements.

Lorenz curves in (a) and (b) show the experimental results for DPMUR and DSMUR with states $\vert {\psi }_{\pi /4,\phi }\rangle$, and the Lorenz curves in (c) and (d) exhibit DPMUR and DSMUR with states $\vert {\psi }_{\theta ,\pi /4}\rangle$. Black curves represent the Lorenz curves of previous bounds t (s(1/2)), and the Lorenz curves of our improved bounds ${{{\mathcal{F}}}}({{{\boldsymbol{t}}}})$ (${{{\mathcal{F}}}}({{{\boldsymbol{s}}}}(1/2))$) are highlighted in red. The dotted lines marked with different colors indicate DPMUR and DSMUR for the state in different parameters. Since the Lorentz curve is plotted by a series of coordinate points $\{(k,\sum\nolimits_{i=1}^{k}x_{i})_{k=0}^{n}\}$, the coordinate axis is not marked with a title. Note that for the measurement and state we choose in the four-dimensional Hilbert space, n = 16 for DPMUR and n = 8 for DSMUR.

We also verify the DPMUR and DSMUR with three measurements, and the experimental results are shown in Fig. 4. Figure 4a, b show the Lorentz curves of probability vectors for DPMUR and DSMUR by performing measurements (11) on the states $\vert {\psi }_{\pi ,\phi }\rangle$, respectively. For measurements C₁, C₂ and C₃, the bound ${{{\mathcal{F}}}}\left({{{{\boldsymbol{t}}}}}^{{\prime} }\right)$ for DPMUR is given by $\left(0.7773,0.2227\right)$ and the bound ${{{\mathcal{F}}}}\left({{{{\boldsymbol{s}}}}}^{{\prime} }\left(1/3\right)\right)$ for DSMUR is given by $\left(1,1,0.7583,0.2417\right)/3$, and the Lorenz curves of these bounds marked in black are shown in Fig. 4a, b. We see that the joint uncertainties associated with different parameters ϕ of the states $\left\vert {\psi }_{\pi ,\phi }\right\rangle$ are marjorized by our bounds ${{{\mathcal{F}}}}\left({{{{\boldsymbol{t}}}}}^{{\prime} }\right)$ and ${{{\mathcal{F}}}}\left({{{{\boldsymbol{s}}}}}^{{\prime} }\left(1/3\right)\right)$. Furthermore, entropies are important tools in quantum information theory, and they are closely related to the majorization. From the properties of majorization, it follows the entropic uncertainty relations ${\sum }_{i}H\left({C}_{i}\right)\,\geqslant \, H\left({{{\mathcal{F}}}}\left({{{{\boldsymbol{t}}}}}^{{\prime} }\right)\right)$ and ${\sum }_{i}H\left({C}_{i}\right)\,\geqslant\, H\left(3{{{\mathcal{F}}}}\left({{{{\boldsymbol{s}}}}}^{{\prime} }\left(1/3\right)\right)\right)$ with H stands for the Shannon entropy. All of this can be seen in Fig. 4c, d.

Fig. 4: Experimental results of DPMUR and DSMUR with three measurements.

a, b show the Lorenz curves of probability vectors for DPMUR and DSMUR with states $\vert {\psi }_{\pi ,\phi }\rangle$, respectively. The Lorentz curves of the bounds ${{{\mathcal{F}}}}\left({{{{\boldsymbol{t}}}}}^{{\prime} }\right)$ and ${{{\mathcal{F}}}}\left({{{{\boldsymbol{s}}}}}^{{\prime} }\left(1/3\right)\right)$) are shown in black curve. c, d show the Shannon entropic uncertainty relations by performing measurements C₁, C₂, C₃ on the states $\vert {\psi }_{\pi ,\phi }\rangle$ and $\vert {\psi }_{\theta ,\pi /2}\rangle$, respectively. The curves marked with magenta, green, and blue stand for the Shannon entropy of probability distributions associated with measurements C₁, C₂ and C₃; that are $H\left({C}_{1}\right)$, $H\left({C}_{2}\right)$ and $H\left({C}_{3}\right)$, and the red curves represent their sum of uncertainties ${\sum }_{i}H\left({C}_{i}\right)$. The dotted line ($H\left({{{\mathcal{F}}}}\left({{{{\boldsymbol{t}}}}}^{{\prime} }\right)\right)=0.7651$) and solid line ($H\left(3{{{\mathcal{F}}}}\left({{{{\boldsymbol{s}}}}}^{{\prime} }\left(1/3\right)\right)\right)=0.7979$) show the Shannon entropy of bounds for DPMUR and DSMUR.

Discussion

Our guessing game formalism of MURs enable us to classify DPMUR and DSMUR into spatially-separated and temporally-separated joint uncertainties accordingly, which differs from previous developments and, more important, exhibit the essential differences of physical features between DPMUR and DSMUR theoretically. We also experimentally verify strong MURs in the photonic system. In order to present the majorization relation, we use Lorentz curve to show it more intuitively. The experimental data are in good agreement with the theoretical prediction. The errors in our experiment mainly come from the inaccuracy of angles of the wave plates and the imperfect interference visibility of the interferometer. Furthermore, it is advantageous to apply the techniques of flatness process to tighter the bounds of MURs, and its efficiency is confirmed by our experiment. The existence of MURs provides tremendous flexibility in formulating uncertainty relations, and greatly enhance our understanding of quantum mechanics. Therefore, the guessing game formalism, and tighter bounds, as well as the corresponding experimental investigation presented in this work would deeper our knowledge of the quantum world.

Methods

Experimental setup

The experimental setup used for verifications of DPMUR and DSMUR is shown in Fig. 2. It consists of a single-photon source module, a state-preparation module, and a measurement module. We will introduce the details of each module in this section.

In the single-photon source module, a 80-mW cw laser with a 404-nm wavelength (linewidth = 5 MHz) pumps a type-II beamlike phase-matching beta-barium-borate (BBO, 6.0 × 6.0 × 2.0 mm³, θ = 40.98°) crystal to produce a pair of photons with wavelength λ = 808 nm. After being redirected by mirrors and passing through the interference filters (IF, Δλ = 3 nm, λ = 808 nm), the photon pairs generated in spontaneous parametric down-conversion are coupled into single-mode fibers separately. One photon is detected by a single-photon detector acting as a trigger. The coincidence counts are approximately 5 × 10³ per second.

In the state preparation module, we prepare a family of 4-dimensional states with parameters θ and ϕ, $\left\vert {\psi }_{\theta ,\phi }\right\rangle =\cos \theta \sin \phi \left\vert 0\right\rangle +\cos \theta \cos \phi \left\vert 1\right\rangle +\sin \theta \left\vert 2\right\rangle +0\left\vert 3\right\rangle$, which is encoded by four modes of a single photon. States $\left\vert 0\right\rangle$ and $\left\vert 1\right\rangle$ are encoded by different polarizations of the photon in the lower mode, and $\left\vert 2\right\rangle$ and $\left\vert 3\right\rangle$ are encoded by polarization of the photon in the upper mode. The beam displacer (BD) causes the vertical polarized photons to be transmitted directly, and the horizontal polarized photons to undergo a 4 mm lateral displacement. When the photon passes through a half-wave plate (H₁) with a certain setting angle, it is split by BD1 into two parallel spatial modes—upper and lower modes. Therefore the photon is prepared in the desired state $\left\vert {\psi }_{\theta ,\phi }\right\rangle$, with parameters θ and ϕ are controlled by the plates H₁ and H₂, respectively.

In the measurement module, device a is used to realize measurements A and C₁. In the presence of quarter-wave plates with an angle of 45°, device b is used to realize measurement B, and the setting angles of H₃–H₆ are 45°, 0°, 22. 5°, and 22. 5°. On the other hand, in the absence of quarter-wave plates, device b is exploited to implement measurement C₂(C₃) when the setting angles of H₃–H₆ are 22. 5°, 0°(45°), 27. 4°, and 0°.