An elegant scheme of self-testing for multipartite Bell inequalities

Abstract

Self-testing is the most accurate form of certification of quantum devices. While self-testing in bipartite Bell scenarios has been thoroughly studied, self-testing in the more complex multipartite Bell scenarios remains largely unexplored. We present a simple and broadly applicable self-testing scheme for N-partite correlation Bell inequalities with two binary outcome observables per party. To showcase the versatility of our proof technique, we obtain self-testing statements for the MABK and WWWŻB family of linear Bell inequalities and Uffink’s family of quadratic Bell inequalities. In particular, we show that the N-partite MABK and Uffink’s quadratic Bell inequalities self-test the GHZ state and anti-commuting observables for each party. While the former uniquely specifies the state, the latter allows for an arbitrary relative phase. To demonstrate the operational relevance of the relative phase, we introduce Uffink’s complex-valued N partite Bell expression, whose extremal values self-test the GHZ states and uniquely specify the relative phase.

Introduction

One of the most striking features of quantum theory is the deviation of its predictions for Bell experiments from the predictions of classical theories with local casual (hidden variable) explanations¹. This phenomenon is captured by quantum violation of statistical inequalities, which are satisfied by all local realistic theories, referred to as Bell inequalities². Experimental demonstrations of the loophole-free violation of such inequalities (e.g., refs. ^3,4,5) imply the possibility of sharing intrinsically random private numbers among an arbitrary number of spatially separated parties which power unconditionally secure private key distribution schemes (for more information on Device-independent quantum cryptography see refs. ^6,7,8,9,10). Such applications of Bell non-locality follow from the fact that the extent of Bell inequality violation can uniquely identify the specific entangled quantum states and measurements, a phenomenon referred to as self-testing (see refs. ^11,12 for initial contributions and the recent review of the progress till now see ref. ¹³).

Self-testing statements are the most accurate form of certifications for quantum systems. Self-testing schemes allow us to infer the underlying physics of a quantum experiment, i.e., the state and the measurements (up to local isometry), without any characterization of the internal workings of the measurement devices, and based only on the observed statistics, i.e., treating the measurement devices as black boxes with classical inputs and outputs. Self-testing has found many applications in several areas like device-independent randomness generation^8,14, quantum cryptography⁹, entanglement detection¹⁵, delegated quantum computing^16,17. While self-testing in the bipartite Bell scenarios has been thoroughly studied, self-testing in more complex multipartite Bell scenarios (see Fig. 1) remains largely unexplored.

Fig. 1: Schematic representation of the correlations in multipartite Bell scenarios.

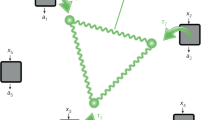
This graphic is a schematic representation of the correlations in multipartite (involving arbitrary number N of spatially separated parties) Bell scenarios. Just like the bipartite Bell scenarios, the correlations which admit local hidden variable explanations form a convex polytope ${{{\mathcal{L}}}}$ (shiny blue small horizontal square), whose facets are the N-party MABK inequalities [Eq. (2)] (red edges). However, the convex set of biseparable quantum correlations ${{{{\mathcal{Q}}}}}_{N-1}$ (sky blue disk) does not form a polytope. Consequently, the linear inequalities such as the MABK [Eq. (2)] (pink edges of the large horizontal square) and Svetlichny inequalities [Eq. (3)] (green edges of the tilted square) do not form tight witness of genuine multipartite quantum non-locality. As the boundary of biseparable quantum correlations (black circle) is non-linear, Uffink’s quadratic inequalities [Eq. (4)] form tighter witnesses of genuine multipartite quantum non-locality.

In a multipartite setting, self-testing has been demonstrated for graph states using stabilizer operators¹⁸. Self-testing of multipartite graph states and partially entangled Greenberger-Horne-Zeilinger (GHZ)¹⁹ states has been demonstrated using a stabilizer-based approach, and Bell inequalities explicitly constructed for the state²⁰. In general, multipartite Bell inequalities explicitly tailored for self-testing of a multipartite entangled state can be obtained using convex optimization techniques such as linear programming and semi-definite programming (SDP)^17,21,22,23. However, the Bell inequalities obtained in this way are just suitable candidates for the self-testing of the given multipartite states, and the potential self-testing statements must be verified using numerical techniques (such as the Swap method), which tend to be computationally expensive for multipartite scenarios with more than four parties. Completely analytical self-testing statements have also been obtained for multipartite states such as the W and the Dicke states by reprocessing self-testing protocols of bipartite states^24,25,26. Furthermore, parallel self-testing statements for multipartite states can be obtained using categorical quantum mechanics²⁷. Finally, the Mayers-Yao criterion can also be utilized for self-testing of graph states when the underlying graph is a triangular lattice²⁸.

In this article, we prove self-testing statements for multipartite Bell scenarios without relying on the Bell-operator dependent sum-of-squares decomposition²⁹. Consequently, our methodology immediately extends to all multipartite Bell scenarios, where each spatially separated party has two observables with binary outcomes ±1. To exemplify our proof technique, we obtain self-testing statements for N party Mermin-Ardehali-Belinskii-Klyshko (MABK)^30,31 and Werner-Wolf-Weinfurter-Żukowski-Brukner (WWWŻB)^32,33,34 family of linear Bell inequalities. Moreover, our methodology enables the recovery of self-testing statements for Bell functions which are not only the mean value of a Hermitian operator. Specifically, to showcase the versatility of our methodology, we obtain self-testing statements for the maximal violation of N party Uffink’s quadratic Bell inequalities, which form tight witnesses of genuine multipartite non-locality, and the novel Uffink’s complex-valued N partite Bell expressions³⁵.

The paper is organized as follows. First, in the Results section we recall the formal definition of self-testing. Then, we present the requisite preliminaries and specify the families of multipartite Bell inequalities we consider in this article. Next, we develop the mathematical preliminaries of the self-testing scheme. In particular, we show that the observables of each party in two-setting binary outcome multipartite Bell scenarios can always be simultaneously represented as anti-diagonal matrices. Next, we utilize this anti-diagonal matrix representation to obtain self-testing statements for the maximal violations of N party MABK and tripartite WWWŻB family of linear (on correlators) Bell inequalities. While the former serves to benchmark our scheme, the latter demonstrates the spectrum of situations one can encounter. Finally, we obtain self-testing statements for the maximal violation of N party Uffinik’s quadratic Bell inequalities and, at the very end of the Results section, we present the self-testing statements for the N partite Uffink’s complex-valued Bell expressions. Next, we provide a brief discussion about the robustness of the self-testing statements obtained in this work. Finally, we conclude by providing a brief summary of our work and potential application.

Results

Before presenting our results, let us first introduce the requisite preliminaries.

Self-testing in Bell scenarios

A Bell scenario describes the operational setup of a Bell experiment by specifying the following three components: (1) the number of spatially separated parties, (2) the number of inputs of each party specifying their measurement settings, (3) the number of outcomes corresponding to each input per party specifying the measurement outcomes for each measurement setting for each party. Each party performs measurements on a quantum system they share. As there are no assumptions on the internal working mechanism of the experimental devices, we may consider the devices to be mere black boxes, capable of receiving inputs (measurement settings) and generating outputs (measurement outcomes). The parties perform measurements based on their inputs and record the corresponding measurement outcomes, and estimate the conditional joint probability distributions governing their devices. Now, the question is, what can we can deduce from these experimental statistics? Specifically, can we make statements describing the underlying physics, i.e., the quantum state and measurements? Such statements are broadly referred to as self-testing statements.

Formally, we say that a given Bell scenario entailing N parties, ${\{{{{{\mathcal{A}}}}}_{j}\}}_{j = 1}^{N}$, each measuring two observables, ${\bar{A}}^{(j)}$, ${\bar{A}}^{{\prime}{(j)}}$ and sharing a state $\left\vert \bar{\psi }\right\rangle \left\langle \bar{\psi }\right\vert$, self-tests, if the observation of the quantum maximal value B of a given Bell expression ${{{\mathcal{B}}}}$ implies that the state $\left\vert \bar{\psi }\right\rangle$ used in the experiment can be transformed by local unitaries, $\mathop{\bigotimes}\limits_{j}{U}_{{{{{\mathcal{A}}}}}_{j}}$, to a reference state, $\left\vert \psi \right\rangle$, and a separable junk part, $\left\vert {{\Psi }}\right\rangle$, on which the observables act trivially, i.e,

$$\mathop{\bigotimes}\limits_{j}{U}_{{{{{\mathcal{A}}}}}_{j}}\left\vert \bar{\psi }\right\rangle =\left\vert \psi \right\rangle \otimes \left\vert {{\Psi }}\right\rangle .$$

Likewise, the local observables ${\{{\bar{A}}^{(j)}\}}_{j = 1}^{N}$ and ${\{{\bar{A}}^{{\prime} {(j)}}\}}_{j = 1}^{N}$, satisfy,

$${U}_{{{{{\mathcal{A}}}}}_{j}}{\bar{A}}^{(j)}{({U}_{{{{{\mathcal{A}}}}}_{j}})}^{{\dagger} }={A}^{(j)}\otimes {\mathbb{1}},$$

$${U}_{{{{{\mathcal{A}}}}}_{j}}{\bar{A}}^{{\prime}{(j)}}{({U}_{{{{{\mathcal{A}}}}}_{j}})}^{{\dagger} }={A}^{{\prime}{(j)}}\otimes {\mathbb{1}},$$

where the joint observables $\mathop{\bigotimes}\limits_{j}{O}^{(j)}$ where ${O}^{(j)}\in \{{A}^{(j)},{A}^{{\prime}{(j)}}\}$ act on the Hilbert space of $\left\vert \psi \right\rangle$, and the tuple $\{\left\vert \psi \right\rangle ,{\{{A}^{(j)},{A}^{{\prime}{(j)}}\}}_{j}\}$ maximizes the given Bell expression, i.e., ${{{\mathcal{B}}}}(\{\left\vert \psi \right\rangle ,{\{{A}^{(j)},{A}^{{\prime}{(j)}}\}}_{j}\})=B$.

The original idea of self-testing was presented in ref. ¹¹ by Mayers and Yao. Over the last few years, a great deal of work has been done in this area, primarily focused on bipartite Bell scenarios. However, self-testing in multipartite Bell scenarios remains relatively unexplored. In this paper, we obtain self-testing statements for multipartite Bell inequalities, introduced in the next section.

Two-setting N-party correlation Bell inequalities

This section presents the requisite preliminaries and specifies the families of Bell inequalities considered in this article. Specifically, here we consider multipartite Bell scenarios entailing N spatially separated (hence non-signaling) parties. We restrict ourselves to Bell scenarios where each party ${{{{\mathcal{A}}}}}_{j}$, where j ∈ {1, …, N}, has two binary outcome observables ${A}^{(j)},{A}^{{\prime}{(j)}}$ (Since there is no restriction on dimension, we can always take the measurements to be projective, in light of Naimark’s dilation Theorem. The projectivity of measurements is a distinguishing feature of a broadly subscribed viewpoint on quantum theory, namely, “The Church of the larger Hilbert space”). In contrast to the well-studied bipartite Bell scenarios, multipartite scenarios are substantially richer in complexity. While the notion of multipartite locality is an obvious extension of bipartite locality, multipartite behaviors can be non-local in many distinct ways. Apart from this, the most significant impediment in obtaining self-testing statements for multipartite Bell scenarios is that they do not admit simplifying characterizations such as Schmidt decomposition of the shared entangled state, unlike the bipartite Bell scenarios.

Typically, Bell inequalities comprise a Bell expression and a corresponding local causal bound. The violation of Bell inequalities witnesses the non-locality of the underlying behaviors. In the rest of this section, we introduce the families of multipartite Bell inequalities, for which we demonstrate self-testing statements using our proof technique.

Linear inequalities

The most frequently used Bell inequalities comprise Bell expressions which are linear expressions of observed probabilities. Our self-testing argument is immediately applicable for any Bell inequality whose Bell expression is the mean of any linear combination of N party operators of the form $\mathop{\bigotimes }\nolimits_{i=1}^{N}{O}^{(i)}$, where ${O}^{(i)}\in \{{A}^{(i)},{A}^{{\prime}{(i)}}\}$. Among such linear Bell inequalities, we consider the Werner-Wolf-Weinfurter-Żukowski-Brukner(WWWŻB) families of correlation Bell inequalities for which there exists a well-defined systematic characterization³⁶. The Bell operator for the WWWŻB family of Bell inequalities has the following general form,

$${{{{\mathcal{W}}}}}_{N}=\frac{1}{{2}^{N}}\mathop{\sum}\limits_{{s}_{1},...,{s}_{N}=\pm 1}S({s}_{1},...,{s}_{N})\mathop{\bigotimes }\limits_{j=1}^{N}({A}^{(j)}+{s}_{j}{A}^{{\prime}{(j)}}),$$

(1)

where S(s₁, . . . , s_N) is an arbitrary function of the indices s₁, . . . , s_N ∈ {−1, 1} with binary outcomes ±1. Every tight (WWWŻB) inequality is given by $\langle {{{{\mathcal{W}}}}}_{N}\rangle {\le }_{{{{\mathcal{L}}}}}1$, where $\langle O\rangle ={\rm{Tr}}\{\rho O\}$ is the expectation value of the linear operator O with respect to the quantum state ρ, and ${\le }_{{{{\mathcal{L}}}}}$ signifies that the inequality holds for all correlations which admit local hidden variable explanations (${{{\mathcal{L}}}}$)³⁷.

Next, we introduce a sub-family of (WWWŻB) Bell inequalities, the Mermin-Ardehali-Belinskii-Klyshko (MABK) family of inequalities, featuring one inequality for any number N of parities^30,31,38. Moreover, in the following subsection, we introduce non-linear (quadratic) Bell inequalities composed of these MABK inequalities. The N-party MABK operators can be obtained recursively as,

$$\begin{array}{ll}{{{{\mathcal{M}}}}}_{N}\,=\,\frac{1}{2}\left({{{{\mathcal{M}}}}}_{N-1}\otimes ({A}^{(j)}+{A}^{{\prime} {(j)}})\right.\\ \qquad\quad\;\;\left.+\,{{{{\mathcal{M}}}}^{\prime} }_{N-1}\otimes ({A}^{(j)}-{A}^{{\prime} {(j)}})\right)\\ \qquad\,\, \,=\,\frac{1}{{2}^{\frac{N+1}{2}}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{\bigotimes}\limits_{j=1}^{N}({A}^{(j)}+\iota {A}^{{\prime} {(j)}})\right.\\ \qquad\quad\;\;\,\left.+\,{\left(\frac{1+\iota}{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{\bigotimes }\limits_{j=1}^{N}({A}^{(j)}-\iota {A}^{{\prime} {(j)}})\right),\end{array}$$

(2)

where the complimentary MABK Bell expression ${{{{\mathcal{M}}}}}_{N-1}^{{\prime} }$ has the same form as ${{{{\mathcal{M}}}}}_{N-1}$ but with all A^(j) and ${A}^{{\prime}{(j)}}$ interchanged. The corresponding Bell inequalities are of the form, $\langle {{{{\mathcal{M}}}}}_{N}\rangle {\le }_{{{{\mathcal{L}}}}}1$. Whereas the maximum attainable values of $\langle {{{{\mathcal{M}}}}}_{N}\rangle$ for biseparable ${{{{\mathcal{Q}}}}}_{N-1}$, and generic quantum correlations ${{{\mathcal{Q}}}}$ are ${2}^{\frac{N-2}{2}}$, and ${2}^{\frac{N-1}{2}}$, respectively. The maximal quantum value can be attained with anti-commuting local observables and the maximally entangled N-partite GHZ state^39,40,41.

Finally, we present yet another relevant sub-family of the (WWWŻB) inequalities, referred to as Svetlichny inequalities³⁵, which were explicitly conceived to witness genuine N-partite non-locality. Moreover, the quadratic Bell inequalities featured in the following subsection can also be composed of N-partite Svetlichny-Bell inequalities. The Svetlichny operator can be formed of MABK operators [Eq. (2)] in the following way,

$${{{{\mathcal{S}}}}}_{N}^{\pm}=\left\{\begin{array}{l}{2}^{k-1}\left({\left(-1\right)}^{\frac{k(k\pm 1)}{2}}{{{{\mathcal{M}}}}}_{N}^{\pm},\right.\\ ({{{\rm{for}}}}\,N=2k);\\ \left.{2}^{k\pm 1}({(-1)}^{\frac{k(k\pm 1)}{2}}{{{{\mathcal{M}}}}}_{N}\mp {(-1)}^{\frac{k(k\mp 1)}{2}}{{{{\mathcal{M}}}}{\prime} }_{N})\right),\\ ({{{\rm{for}}}}\,N=2k+1),\end{array}\right.$$

(3)

where ${{{{\mathcal{M}}}}}_{N}^{+}$ is equivalent to ${{{{\mathcal{M}}}}}_{N}$[Eq. (2)] and ${{{{\mathcal{M}}}}}_{N}^{-}$ is equivalent to ${{{{\mathcal{M}}}}{\prime} }_{N}$. The corresponding Svetlichny inequalities are of the form, $\langle {{{{\mathcal{S}}}}}_{N}^{\pm }\rangle {\le }_{{{{{\mathcal{Q}}}}}_{N-1}}{2}^{N-1}{\le }_{{{{\mathcal{Q}}}}}{2}^{N-\frac{1}{2}}$.

Quadratic inequalities

In bipartite Bell scenarios, without loss of generality, it is enough to consider linear Bell inequalities to witness non-locality as the set of behaviors that admit a local casual explanation form a convex polytope demarcated by linear facet inequalities. In contrast to the bipartite case, non-linear Bell inequalities form tighter witnesses of genuine multipartite non-locality. In multipartite Bell scenarios, the convex set of biseparable quantum behaviors does not form a polytope. Consequently, Uffink’s quadratic Bell inequalities form stronger witnesses of genuine multipartite non-locality than the linear inequalities. There are two distinct families of N party quadratic Bell inequalities formed of the MABK [Eq. (2)] and Svetlichny [Eq. (3)], families of linear inequalities, ${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}$ and ${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{S}}}}}$, respectively, which have the form

$${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}={\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle }^{2}+{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }^{2}{\le }_{{{{{\mathcal{Q}}}}}_{N-1}}{2}^{N-2}{\le }_{{{{\mathcal{Q}}}}}{2}^{N-1},$$

(4)

$${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{S}}}}}={\left\langle {{{{\mathcal{S}}}}}_{N}^{+}\right\rangle }^{2}+{\left\langle {{{{\mathcal{S}}}}}_{N}^{-}\right\rangle }^{2}{\le }_{{{{{\mathcal{Q}}}}}_{N-1}}{2}^{2N-2}{\le }_{{{{\mathcal{Q}}}}}{2}^{2N-1},$$

(5)

Characterizing local observables

In this section, we obtain a characterization for the binary outcome local observables A = A^(j) and $A^{\prime} ={A}^{{\prime}{(j)}}$ on an arbitrary Hilbert space ${{{\mathcal{H}}}}={{{{\mathcal{H}}}}}^{(j)}$ for any given party ${{{{\mathcal{A}}}}}_{j}$, where j ∈ {1, …, N}. As in Bell scenarios, there is no restriction on the dimension of the underlying Hilbert space, using Naimark’s dilation Theorem, without loss of generality, we can take the observables A and $A^{\prime}$ to be projective, i.e., ${A}^{2}={A}^{{\prime}{2}}={\mathbb{1}}$. First, via the following lemma, we demonstrate that the second observable $A^{\prime}$ can be split into two observables, one which commutes with the first observable A and one which anti-commutes with A,

Lemma 1

Given any two binary outcome projective observables A and $A^{\prime}$, $A^{\prime}$ can be decomposed as the sum of two observables $-{\mathbb{1}}\le {A}_{-}^{{\prime} }\le {\mathbb{1}}$ and $-{\mathbb{1}}\le {A}_{+}^{{\prime} }\le {\mathbb{1}}$, such that $[A,\,A^{{\prime}}_{+}]=0$, $\{A,\,A^{{\prime} }_{-}\}=0$, $\{{A}_{+}^{{\prime} },{A}_{-}^{{\prime} }\}=0$ and ${({A}_{+}^{{\prime} })}^{2}+{({A}_{-}^{{\prime} })}^{2}={\mathbb{1}}$.

Proof

Without loss of generality, the binary outcome projective observable A can be represented as a diagonal matrix with positive and negative eigenvalues grouped together,

$$A=\left(\begin{array}{ll}{{\mathbb{1}}}_{m}&0\\ 0&-{{\mathbb{1}}}_{n}\end{array}\right),$$

(6)

where ${{\mathbb{1}}}_{m}$ is the m × m identity operator. With respect to A, the binary outcome projective observable $A^{\prime}$ has the following generic matrix representation,

$$A^{\prime} =\left(\begin{array}{ll}{D}_{1}&{D}_{2}\\ {D}_{2}^{{\dagger} }&{D}_{3}\end{array}\right).$$

(7)

such that,

$${A}_{-}^{{\prime} }=\left(\begin{array}{ll}0&{D}_{2}\\ {D}_{2}^{{\dagger} }&0\end{array}\right)\,,$$

(8)

$${A}_{+}^{{\prime} }=\left(\begin{array}{ll}{D}_{1}&0\\ 0&{D}_{3}\end{array}\right)\,.$$

(9)

Clearly, $[A,\,A^{\prime}_{+}]=0$, and $\{A,\,A^{\prime}_{-}\}=0$. As $A^{\prime}$ is projective we have,

$$\begin{array}{l}{(A^{\prime} )}^{2}\,=\,{({A}_{+}^{{\prime} })}^{2}+{({A}_{-}^{{\prime} })}^{2}+\{{A}_{+}^{{\prime} },{A}_{-}^{{\prime} }\}\\ \,\,\,\,\,\quad\quad=\,\left(\begin{array}{ll}{D}_{1}^{2}+{D}_{2}{D}_{2}^{{\dagger} }\quad{D}_{1}{D}_{2}+{D}_{2}{D}_{3}\\ {D}_{2}^{{\dagger} }{D}_{1}+{D}_{3}{D}_{2}^{{\dagger} }\quad{D}_{2}^{{\dagger} }{D}_{2}+{D}_{3}^{2}\end{array}\right)\end{array}$$

(10)

$$={\mathbb{1}}\,,$$

(11)

which requires the off-diagonal blocks to be zero,

$$\begin{array}{l}\{{A}_{+}^{{\prime} },{A}_{-}^{{\prime} }\}\,=\,\left(\begin{array}{ll}0\quad{D}_{1}{D}_{2}+{D}_{2}{D}_{3}\\ {D}_{2}^{{\dagger} }{D}_{1}+{D}_{3}{D}_{2}^{{\dagger} }\quad0\end{array}\right)\\ \qquad\qquad\,\,\,\,\,=\,0,\end{array}$$

(12)

and leaves ${({A}_{+}^{{\prime} })}^{2}+{({A}_{-}^{{\prime} })}^{2}={\mathbb{1}}$, which completes the proof.

Using the above Lemma, the relation between the eigenvalues of $A^{\prime}$, ${A}_{-}^{{\prime} }$, and ${A}_{+}^{{\prime} }$ can be ascertained to be ${\lambda}^{i}_{{A}^{\prime}}=\pm \sqrt{{({\lambda }_{{A}_{-}^{{\prime} }}^{i})}^{2}+{({\lambda }_{{A}_{+}^{{\prime} }}^{i})}^{2}}=\pm 1$, where ${\lambda }_{\cdot }^{i}$ denotes the i^th eigenvalue⁴². So that the eigenvalues can be without loss of generality taken as $\pm \sin {\theta }_{i}$ and $\pm \cos {\theta }_{i}$ for ${A}_{-}^{{\prime} }$ and ${A}_{+}^{{\prime} }$ respectively.

Next, we show that the spectra of any two anti-commuting observables must be symmetric, and each observable maps the positive eigenspaces to the negative eigenspaces of the other.

Lemma 2

Given any two binary outcome anti-commuting projective observables, A and ${A}_{-}^{{\prime} }$, such that ${A}^{2}={\mathbb{I}}$, their spectra must be symmetric (i.e., if $\left\vert {\psi }_{\lambda }\right\rangle$ is an eigenvector corresponding to the eigenvalue λ, then there exists a unique eigenvector $\left\vert {\psi }_{-\lambda }\right\rangle$ corresponding to the eigenvalue −λ). Moreover, ${A}_{-}^{{\prime} }$ acts on an effective even-dimensional Hilbert space ${\bigoplus }_{i}{E}_{\pm {\lambda }_{i}}^{{A}_{-}^{{\prime} }}$ decomposed into the direct sum of the even-dimensional eigenspaces ${E}_{\pm {\lambda }_{i}}^{{A}_{-}^{{\prime} }}={E}_{{\lambda }_{i}}^{{A}_{-}^{{\prime} }}\oplus {E}_{-{\lambda }_{i}}^{{A}_{-}^{{\prime} }}$. Where, ${E}_{{\lambda }_{i}}^{{A}_{-}^{{\prime} }}$ and ${E}_{-{\lambda }_{i}}^{{A}_{-}^{{\prime} }}$ are eigenspaces corresponding to the non-zero eigenvalues ${\lambda }_{i}^{{A}_{-}^{{\prime} }}$ and $-{\lambda }_{i}^{{A}_{-}^{{\prime} }}$, respectively.

Proof

From the anti-commutation relation it follows that, $A{A}_{-}^{{\prime} }=-{A}_{-}^{{\prime} }A$. As A is unitary and Hermitian, we can take A to the other side to sandwich ${A}_{-}^{{\prime} }$, which leaves us with,

$$A{A}_{-}^{{\prime} }A=-{A}_{-}^{{\prime} }.$$

(13)

Further, taking trace on both sides of Eq. (13) yields,

$${{{\rm{Tr}}}}\{{A}_{-}^{{\prime} }\}=0.$$

(14)

This implies that the observable ${A}_{-}^{{\prime} }$ has a symmetric spectra, i.e., for each eigenvector corresponding to a non-zero eigenvalue λ_i there exists an eigenvector corresponding to the eigenvalue −λ_i, along with the null space or the kernel $ker({A}_{-}^{{\prime} })$. Without loss of generality, we can ignore the kernel as it does not contribute to the violation of Bell inequalities. Hence, we are left with the subspace, ${\bigoplus }_{i}{E}_{\pm {\lambda }_{i}}^{{A}_{-}^{{\prime} }}$, where ${E}_{\pm {\lambda }_{i}}^{{A}_{-}^{{\prime} }}={E}_{{\lambda }_{i}}^{{A}_{-}^{{\prime} }}\oplus {E}_{-{\lambda }_{i}}^{{A}_{-}^{{\prime} }}$ is an even-dimensional subspace corresponding to the non-zero eigenvalues $\pm {\lambda }_{i}^{{A}_{-}^{{\prime} }}$. The diagonalizability of ${A}_{-}^{{\prime} }$ (Hermitian) implies that we can decompose this subspace into the direct sum of these eigenspaces (and the kernel $ker({A}_{-}^{{\prime} })$), which further implies that the effective subspace of such operators can be truncated to an even-dimensional subspace. Finally, as on this truncated subspace, $A{A}_{-}^{{\prime} }\left\vert {\psi }_{{\lambda }_{i}}\right\rangle =-{\lambda }_{i}{A}_{-}^{{\prime} }\left\vert {\psi }_{{\lambda }_{i}}\right\rangle$, where $\left\vert {\psi }_{{\lambda }_{i}}\right\rangle$ is an eigenvector of A corresponding to eigenvalue λ_i = ±1, we conclude that m = n, i.e., A is even-dimensional and has a similarly symmetric spectrum.

Now, as $A^{\prime} ={A}_{+}^{{\prime} }+{A}_{-}^{{\prime} }$, the effective subspaces of ${A}_{+}^{{\prime} }$, $A^{\prime}$, can also be truncated to the same effective even-dimensional subspace as ${A}_{-}^{{\prime} }$. Also, as on this truncated subspace, ${A}_{+}^{{\prime} }{A}_{-}^{{\prime} }\left\vert {\psi }_{{\lambda }_{i}}\right\rangle =-{\lambda }_{i}{A}_{-}^{{\prime} }\left\vert {\psi }_{{\lambda }_{i}}\right\rangle$, where $\left\vert {\psi }_{{\lambda }_{i}}\right\rangle$ is an eigenvector of ${A}_{+}^{{\prime} }$ corresponding to its eigenvalue λ_i, i.e., ${A}_{+}^{{\prime} }$ has a similar symmetric spectrum. Moreover, Lemma 2 yields the following succinct parameterization of the two mutually anti-commuting components of any projective observable,

Corollary 2.1

Given two even-dimensional anti-commuting operators A₊ and A₋ such that ${({A}_{+}^{{\prime} })}^{2}+{({A}_{-}^{{\prime} })}^{2}={\mathbb{1}}$, they can be written in the form,

$$\begin{array}{rcl}{A}_{+| {\theta }_{i}}^{{\prime} }=\cos {\theta }_{i}{B}_{+| {\theta }_{i}}&&{A}_{-| {\theta }_{i}}^{{\prime} }=\sin {\theta }_{i}{B}_{-| {\theta }_{i}}\end{array}$$

(15)

when restricted to the subspace ${E}_{+{\theta }_{i}}^{{A}_{-}^{{\prime} }}\oplus {E}_{-{\theta }_{i}}^{{A}_{-}^{{\prime} }}$ with corresponding eigenvalues $\pm \cos ({\theta }_{i})$ for A₊ and $\pm \sin ({\theta }_{i})$ for A₋, such that the operators ${B}_{\pm | {\theta }_{i}}$ are traceless and projective.

Proof

We have already shown the dimension of the combined eigenspaces ${E}_{{\lambda }_{i}}^{{A}_{-}^{{\prime} }}\oplus {E}_{-{\lambda }_{i}}^{{A}_{-}^{{\prime} }}$ is even. Then the two anti-commuting operators ${A}_{+}^{{\prime} }$ and ${A}_{-}^{{\prime} }$ restricted to this eigenspace, denoted by ${A}_{+| {\theta }_{i}}^{{\prime} }$ and ${A}_{-| {\theta }_{i}}^{{\prime} }$, will only have eigenvalues $\pm \cos {\theta }_{i}$ and $\pm \sin {\theta }_{i}$ respectively, whilst still satisfying ${({A}_{+| {\theta }_{i}}^{{\prime} })}^{2}+{({A}_{-| {\theta }_{i}}^{{\prime} })}^{2}={\mathbb{1}}$. It is then possible to write the same relation in terms of scaled operators, as

$${\cos }^{2}{\theta }_{i}{B}_{+| {\theta }_{i}}^{2}+{\sin }^{2}{\theta }_{i}{B}_{-| {\theta }_{i}}^{2}={\mathbb{1}}.$$

(16)

As a result, the operators ${B}_{\pm | {\theta }_{i}}$ have eigenvalues ±1 that occur in pairs. Therefore, ${{{\rm{Tr}}}}({B}_{\pm | {\theta }_{i}})=0$ and ${B}_{\pm | {\theta }_{i}}^{2}={\mathbb{1}}$.

Using the above results, in such an even-dimensional subspace the following lemma holds.

Lemma 3

Given any two traceless and projective anti-commuting observables B₊ and B₋, the observable $\cos \alpha {B}_{+}+\sin \alpha {B}_{-}$ is also traceless and projective.

Proof

Expanding the square,

$$\begin{array}{l}{\left(\cos \alpha {B}_{+}+\sin \alpha {B}_{-}\right)}^{2}\\ ={\cos }^{2}\alpha {B}_{+}^{2}+{\sin }^{2}\alpha {B}_{-}^{2}+\cos \alpha \sin \alpha \{{B}_{+},{B}_{-}\}\\={\mathbb{1}}.\end{array}$$

(17)

And the trace is simply,

$$\cos \alpha {{{\rm{Tr}}}}({B}_{+})+\sin \alpha {{{\rm{Tr}}}}({B}_{-})=0.$$

(18)

The above lemma shows that in the Bell scenarios considered here, the effective local dimension of any subsystem must be even-dimensional. Now, we present the main ingredient of our self-testing proof technique, i.e., the simultaneous anti-diagonal matrix representation for local observables of each party up to local isometries.

Theorem 4

Given any three binary outcome traceless and projective observables A, B₊, and B₋, such that [A, B₊] = 0, {A, B₋} = 0, and {B₊, B₋} = 0, then these operators have a simultaneous anti-diagonal matrix representation.

Proof

As [A, B₊] = 0, we can take the dimension of the subspace for which the eigenvalues of A and B₊ are equal to be 2d₁, and 2d₂ for the subspace where the eigenvalues differ. Consequently, without loss of generality, by Lemma 2 the operators A, B₊, and B₋ have the following matrix representations,

$$\begin{array}{lll}A=&&\left(\begin{array}{llll}{{\mathbb{1}}}_{{d}_{1}}&\cdot &\cdot &\cdot \\ \cdot &{{\mathbb{1}}}_{{d}_{2}}&\cdot &\cdot \\ \cdot &\cdot &-{{\mathbb{1}}}_{{d}_{2}}&\cdot \\ \cdot &\cdot &\cdot &-{{\mathbb{1}}}_{{d}_{1}}\end{array}\right),\\ {B}_{+}=&&\left(\begin{array}{cccc}{{\mathbb{1}}}_{{d}_{1}}&\cdot &\cdot &\cdot \\ \cdot &-{{\mathbb{1}}}_{{d}_{2}}&\cdot &\cdot \\ \cdot &\cdot &{{\mathbb{1}}}_{{d}_{2}}&\cdot \\ \cdot &\cdot &\cdot &-{{\mathbb{1}}}_{{d}_{1}}\end{array}\right),\\ {B}_{-}=&&\left(\begin{array}{cccc}\cdot &\cdot &\cdot &{U}_{1}\\ \cdot &\cdot &{U}_{2}&\cdot \\ \cdot &{U}_{2}^{{\dagger} }&\cdot &\cdot \\ {U}_{1}{\dagger} &\cdot &\cdot &\cdot \end{array}\right).\end{array}$$

(19)

Since B₋ is projective, U₁ and U₂ must be unitary. Thus, without altering A or B₊ we can take four unitaries V₁, V₂, V₃, V₄, each acting on a different block, such that ${V}_{1}{U}_{1}{V}_{4}^{{\dagger} }={J}_{{d}_{1}}$ and ${V}_{2}{U}_{2}{V}_{3}^{{\dagger} }={J}_{{d}_{2}}$, where J_d is the row-reversed d × d identity matrix.

Consequently, we can now restrict ourselves to considering any one of the d₁ + d₂ two-dimensional subspaces, on which A and B₊ are represented by ±σ_z, while B₋ is projected onto σ_x. Finally, in each of these subspaces, we apply the following unitary transformation,

$$U=\frac{1}{2}\left(\begin{array}{ll}-1+\iota &1+\iota \\ -1+\iota &-1-\iota \end{array}\right),$$

(20)

which corresponds to a rotation by $\frac{2\pi }{3}$ with respect to axis (1, 1, 1), and transforms σ_z → σ_x → σ_y, and bringing all three operators to strictly anti-diagonal form.

Summarizing, the Theorem 4, along with Lemmas 2 and 3 allow us to take the first observable of each party A^(j) to be equivalent to σ_x on all relevant two-dimensional subspaces, while the second operator ${A}^{{\prime}{(j)}}$ can be taken to be ${A}^{{\prime}{(j)}}=\cos {\theta }_{j}{\sigma }_{x}+\sin {\theta }_{j}{\sigma }_{y}$.

We note here that the above thesis also follows from a well-known result, commonly referred to as Jordan’s lemma^43,44, which states that any two dichotomic observables squaring to identity can be simultaneously brought into a block diagonal form with one and two-dimensional blocks. Discarding the one-dimensional blocks as they do not contribute to Bell non-locality, each pair of the remaining two-dimensional blocks, which act as dichotomic observables on the same Hilbert space can be unitarily rotated to σ_x and $\cos {\theta }_{j}{\sigma }_{x}+\sin {\theta }_{j}{\sigma }_{y}$. In fact, Jordan’s lemma has already been used in this way to obtain self-testing statements⁴¹. Therefore, the contents of this section constitute an alternative proof of Jordan’s lemma and the subsequent parametrization.

This theorem forms the key ingredient of our proof technique as it yields the following criterion for self-testing statements obtained in this work,

Lemma 5

The maximum quantum value B of any two-setting two outcome N-partite Bell expression ${{{\mathcal{B}}}}$ composed of N party correlators, self-tests a generalized GHZ state, $\alpha \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert {i}_{j}\right\rangle +\beta \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert \bar{{i}_{j}}\right\rangle$, where i_j ∈ {0, 1} and $\bar{{i}_{j}}=1\oplus {i}_{j}$, if the corresponding Bell operator has a non-degenerate maximum eigenvalue λ_max = B.

Proof

For two-setting binary outcome N partite Bell scenarios, Theorem 4 implies that the local observables of each party have simultaneous anti-diagonal matrix representations. Consequently, any N partite Bell expression ${{{\mathcal{B}}}}$ composed only of N party correlators corresponds to a Bell operator on ${({{\mathbb{C}}}^{2})}^{\otimes N}$ which also has an anti-diagonal matrix representation. Clearly, the maximum value of the Bell expression ${{{\mathcal{B}}}}$ corresponds to the maximum eigenvalue λ_max of the Bell operator. As the eigenvectors of any such anti-diagonal matrix are of the form of generalized GHZ states, $\alpha \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert {i}_{j}\right\rangle +\beta \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert \bar{{i}_{j}}\right\rangle$, where i_j ∈ {0, 1} and $\bar{{i}_{j}}=1\oplus {i}_{j}$, the maximum value B of such a Bell expression self-tests such a state if the maximum eigenvalue λ_max of the Bell operator is non-degenerate.

In the next section, we demonstrate our proof technique and obtain self-testing statements for the MABK family of N party inequalities and tripartite Bell inequalities composed of three-party correlators.

Self-testing statements for multipartite inequalities

In this section, we use the tools developed in the previous section to obtain self-testing statements for linear MABK family of N party inequalities [Eq. (2)], and sketch the proofs for the self-testing statements for all distinct equivalence classes of tripartite WWWŻB facet inequalities [Eq. (1)]. Finally, we obtain self-testing statements for Uffink’s family [Eq. (4)] of non-linear N party inequalities.

N party MABK inequalities

Theorem 6

In order to achieve maximal quantum violation of a N-party MABK inequality, $\langle {{{{\mathcal{M}}}}}_{N}\rangle ={2}^{\frac{N-1}{2}}$, the parties must share a N qubit GHZ state $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where ϕ(N) is the relative phase, ϕ(N) = 0 when N is odd, $\phi (N)=-\frac{\pi }{4}$ when N is even and perform maximally anti-commuting projective measurements A^(j) = σ_x and ${A}^{{\prime}{(j)}}={\sigma }_{y}$ (up to local isometries).

Proof

From Lemma 2 and Theorem 4, without loss of generality, the local observables of any party ${{{{\mathcal{A}}}}}_{j}$, where j ∈ {1, …, N}, can be taken to be,

$$\begin{array}{l}{A}^{(j)}\,=\,{\sigma }_{x},\\ {A}^{{\prime}{(j)}}\,=\,\cos {\theta }_{j}{\sigma }_{x}+\sin {\theta }_{j}{\sigma }_{y},\end{array}$$

(21)

acting on the effective two-dimensional subspace. This parametrization implies that the MABK operator [Eq. (2)]${{{{\mathcal{M}}}}}_{N}$ has the following anti-diagonal matrix representation,

$${{{{\mathcal{M}}}}}_{N}={{{\rm{adiag}}}}\left(\begin{array}{l}\frac{1}{{2}^{\frac{N+1}{2}}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{\Pi}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})\right.\\ \left.+{\left(\frac{1+\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1-\iota {e}^{-\iota {\theta }_{j}})\right)\\ \vdots \\ \frac{1}{{2}^{\frac{N+1}{2}}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{\iota {\theta }_{j}})\right.\\ \left.+{\left(\frac{1+\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1-\iota {e}^{\iota {\theta }_{j}})\right)\end{array}\right),$$

(22)

where adiag represents a matrix with non-zero values only on the anti-diagonal. It is easy to see for any combination, $\forall j\in \{1,\ldots ,N\}:{\theta }_{j}=\pm \!\frac{\pi }{2}$, one of the anti-diagonal elements attains the maximum absolute value of ${2}^{\frac{N-1}{2}}$ while the others vanish.

Recall that the maximum expectation value of an operator corresponds to its highest eigenvalue, attained when the state corresponds to the associated eigenvector. Moreover, the eigenvectors of operators with an anti-diagonal matrix representation are of the generic form, $\alpha \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert {i}_{j}\right\rangle +\beta \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert \bar{{i}_{j}}\right\rangle$, where i_j ∈ {0, 1} and $\bar{{i}_{j}}=1\oplus {i}_{j}$. Now, taking the expectation value of ${{{{\mathcal{M}}}}}_{N}$ with respect to any one of these states selects the sum of a pair of (equidistant from the top and the bottom) anti-diagonal elements. As each such pair is equivalent to the rest up-to local rotations, we can, without loss of any generality, consider the state, $\left\vert {\psi }_{N}\right\rangle =\alpha {\left\vert 0\right\rangle }^{\otimes N}+\beta {\left\vert 1\right\rangle }^{\otimes N}$, which effectively yields a weighted sum of the top and bottom anti-diagonal elements of the matrix [Eq. (22)].

Specifically, the expectation value of the Hermitian operator ${{{{\mathcal{M}}}}}_{N}$ for the state $\left\vert {\psi }_{N}\right\rangle$ has the expression,

$$\begin{array}{ll}\left\langle {\psi }_{N}\right\vert {{{{\mathcal{M}}}}}_{N}\left\vert {\psi }_{N}\right\rangle =2{\rm{Re}} \left\{\overline{\alpha }\frac{1}{{2}^{\frac{N+1}{2}}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})\right.\right.\\ \qquad\qquad\qquad\quad\;\;\,\left.\left.+\,{\left(\frac{1+\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1-\iota {e}^{-\iota {\theta }_{j}})\right)\beta \right\},\end{array}$$

(23)

Using the fact that $\forall \alpha ,\beta \in {\mathbb{C}}:\,{\rm{Re}} \,\alpha \beta \le | \alpha \beta | =| \alpha | | \beta |$ we bound $\left\langle {\psi }_{N}\right\vert {{{{\mathcal{M}}}}}_{N}\left\vert {\psi }_{N}\right\rangle$ from above in the following way,

$$\begin{array}{ll}\left\langle {\psi }_{N}\right\vert {{{{\mathcal{M}}}}}_{N}\left\vert {\psi }_{N}\right\rangle \le \,2| \overline{\alpha }| | \beta | | \frac{1}{{2}^{\frac{N+1}{2}}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})\right.\\ \qquad\qquad\qquad\qquad\left.+\,{\left(\frac{1+\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1-\iota {e}^{-\iota {\theta }_{j}})\right)| .\end{array}$$

(24)

As ∣α∣² + ∣β∣² = 1, the maximum value of the above expression can only be attained for $| \alpha | =| \beta | =\frac{1}{\sqrt{2}}$, which picks out $\left\vert GH{Z}_{N}\right\rangle$ as the shared state. Consequently, we retrieve the following upper bound,

$$\begin{array}{ll}\left\langle {\psi }_{N}\right\vert {{{{\mathcal{M}}}}}_{N}\left\vert {\psi }_{N}\right\rangle \le &\left| \frac{1}{{2}^{\frac{N+1}{2}}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})\right.\right.\\ &\left.\left.+{\left(\frac{1+\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1-\iota {e}^{-\iota {\theta }_{j}})\right)\right| .\end{array}$$

(25)

Now, as $| {(\frac{1+\iota }{\sqrt{2}})}^{(N-1){{{\rm{mod}}}}2}| =| {(\frac{1-\iota }{\sqrt{2}})}^{(N-1){{{\rm{mod}}}}2}| =1$ and $| (1+\iota {e}^{-\iota {\theta }_{j}})| =| 2\sin (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})|$ and $| (1-\iota {e}^{-\iota {\theta }_{j}})| =| 2\cos (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})|$, we can further upper bound the above expression as,

$$\begin{array}{ll}\left\langle {\psi }_{N}\right\vert {{{{\mathcal{M}}}}}_{N}\left\vert {\psi }_{N}\right\rangle \le &{2}^{\frac{N-1}{2}}\left(\mathop{{{\Pi }}}\limits_{j = 1}^{N}\left| \sin \left(\frac{\pi }{4}+\frac{{\theta }_{j}}{2}\right)\right| \right.\\ &\left.+\mathop{{{\Pi }}}\limits_{j = 1}^{N}\left| \cos \left(\frac{\pi }{4}+\frac{{\theta }_{j}}{2}\right)\right| \right).\end{array}$$

As, $\forall j:| \sin (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})| \le 1,| \cos (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})| \le 1$, we can further upper bound the above expression by discarding all but three terms corresponding to any i, j, k ∈ {1, …, N}, such that,

$$\begin{array}{l}\left\langle {\psi }_{N}\right\vert {{{{\mathcal{M}}}}}_{N}\left\vert {\psi }_{N}\right\rangle \\ \qquad\le {2}^{\frac{N-1}{2}}\left(\left\vert \sin \left(\frac{2{\theta }_{i}+\pi }{4}\right)\sin \left(\frac{2{\theta }_{j}+\pi }{4}\right)\sin \left(\frac{2{\theta }_{k}+\pi }{4}\right)\right\vert \right.\\ \qquad\quad\left.+\left\vert \cos \left(\frac{2{\theta }_{i}+\pi }{4}\right)\cos \left(\frac{2{\theta }_{j}+\pi }{4}\right)\cos \left(\frac{2{\theta }_{k}+\pi }{4}\right)\right\vert \right)\\ \qquad\le {2}^{\frac{N-1}{2}},\end{array}$$

(26)

where the proof of the second inequality has been deferred to the Supplementary Note. In the Supplementary Note, we also show that this inequality can only be saturated when ${\theta }_{i}={\theta }_{j}={\theta }_{k}=\frac{\pi }{2}$. As the choice of i, j, k ∈ {1, …, N} is completely arbitrary, the inequality can only be saturated when $\forall j\in \{1,\ldots ,N\}:{\theta }_{j}=\frac{\pi }{2}$, i.e., when for each party the local observables maximally anti-commute. As these settings maximize the value of ${{{{\mathcal{M}}}}}_{N}$ only for a unique pair of equidistant anti-diagonal entries, the state must be $\left\vert GH{Z}_{N}\right\rangle \equiv \frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where ϕ(N) = 0 when N is odd, and $\phi (N)=-\frac{\pi }{4}$ when N is even, up to auxiliarly degrees of freedom on which the measurements act trivially, and local basis transformations. This further implies that the actual shared state could be of the form $\left\vert GH{Z}_{N}\right\rangle \bigotimes \left\vert {{\Psi }}\right\rangle$ up to local unitaries, where the arbitrary state $\left\vert {{\Psi }}\right\rangle$ on auxiliary degrees of freedom does not contribute to the operational Bell violation and thus is referred to as the junk state.

We note here that the same proof technique extends to the complimentary MABK inequalities, ${{{{\mathcal{M}}}}{\prime} }_{N}$, defined in “Results: Two-setting N-party correlation Bell inequalities”, as well, to yield the corresponding self-testing statements, summarized in the following Corollary.

Corollary 6.1

In order to achieve the maximal quantum violation of a N-party complimentary MABK inequality, $\langle {{{{\mathcal{M}}}}{\prime} }_{N}\rangle ={2}^{\frac{N-1}{2}}$, the parties must share a N qubit GHZ state $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where $\phi (N)=\frac{\pi }{2}$ when N is odd, $\phi (N)=\frac{\pi }{4}$ when N is even and perform maximally anti-commuting projective measurements A^(j) = σ_x and ${A}^{{\prime}{(j)}}={\sigma }_{y}$ (up to local isometries).

The proof follows a relatively straightforward modification of the proof of Theorem 6. However, these self-testing statements will be used in the next section for obtaining self-testing of Uffink’s quadratic inequalities. Moreover, the proof technique readily applies to the Svetlichny family of N-party inequalities as they are composed of the N-party MABK inequalities. Furthermore, the proof technique enables self-testing of a much broader class of N-party WWWŻB inequalities. To demonstrate this, we sketch the proofs for self-testing of tripartite WWWŻB inequalities [Eq. (1)].

Tripartite WWWŻB inequalities

In the case of tripartite Bell scenarios where each party has two input and output respectively, we have a 26-dimensional local correlation polytope that has 64 vertices and 53,856 faces⁴⁵. These faces can be grouped into 46 equivalence classes of Bell inequalities listed in ref. ⁴⁶, and out of which, we consider the non-trivial facet inequalities, which are composed of only three-party correlators and can be grouped into the following four equivalence classes.

The first class is composed of correlation inequalities equivalent (up-to relabeling) to the Mermin’s inequality $\left\langle {{{{\mathcal{M}}}}}_{3}\right\rangle \le 1$,

$$\begin{array}{l}\frac{1}{2}\left(\left\langle \left({A}^{(1)}{A}^{(2)}{A}^{{\prime}{(3)}}\right.\right\rangle +\left\langle {A}^{(1)}{A}^{{\prime}{(2)}}{A}^{(3)}\right\rangle \right.\\ \left.+\left\langle {A}^{{\prime}{(1)}}{A}^{(2)}{A}^{(3)}\right\rangle -\left\langle \left.{A}^{{\prime}{(1)}}{A}^{{\prime}{(2)}}{A}^{{\prime}{(3)}}\right)\right\rangle \right)\le 1.\end{array}$$

For these inequalities, the proof of Theorem 6 directly applies³⁷. As a consequence, we retrieve the tripartite GHZ state $\left\vert GH{Z}_{3}\right\rangle$ as well as maximally anti-commuting local observables as necessary ingredients for the maximal quantum violation 2.

The second equivalence class of tripartite inequalities is that of unbalanced inequalities, which can be found in the ref. ⁴⁷ as the seventh inequality in Table I, and also specified below,

$$\begin{array}{l}\left(3\left\langle {A}^{(1)}{A}^{(2)}{A}^{(3)}\right\rangle +\left\langle {A}^{(1)}{A}^{(2)}{A}^{{\prime}{(3)}}\right\rangle \right.\\ +\left\langle {A}^{(1)}{A}^{{\prime}{(2)}}{A}^{(3)}\right\rangle +\left\langle {A}^{{\prime}{(1)}}{A}^{(2)}{A}^{(3)}\right\rangle \\ -\left\langle {A}^{(1)}{A}^{{\prime}{(2)}}{A}^{{\prime} {(3)}}\right\rangle -\left\langle {A}^{{\prime}{(1)}}{A}^{(2)}{A}^{{\prime}{(3)}}\right\rangle \\ \left.-\left\langle {A}^{{\prime}{(1)}}{A}^{{\prime}{(2)}}{A}^{(3)}\right\rangle +\left\langle {A}^{{\prime}{(1)}}{A}^{{\prime}{(2)}}{A}^{{\prime}{(3)}}\right\rangle \right)\le 4.\end{array}$$

The corresponding operator has an anti-diagonal matrix representation with values of the form,

$$4+(-1+{e}^{\iota {k}_{1}{\theta }_{1}})(-1+{e}^{\iota {k}_{2}{\theta }_{2}})(-1+{e}^{\iota {k}_{3}{\theta }_{3}}),$$

(27)

where (k₁, k₂, k₃ ∈ {−1, 1}). Unlike the MABK class of inequalties the absolute values of these anti-diagonal terms are maximized when $\cos {\theta }_{j}=-\frac{1}{3}$. Thus, yet again, the tripartite GHZ state $\left\vert GH{Z}_{3}\right\rangle$ is distinguished, but non maximally anti-commuting local observables are required for maximal quantum violation, $\frac{20}{3}$, of these inequalities.

We will next discuss the equivalence class of the extended CHSH inequalities of the form given below, which is listed as the third inequality in Table I of the ref. ⁴⁶,

$$\begin{array}{l}\frac{1}{2}\left(\left\langle {A}^{(1)}{A}^{(2)}{A}^{(3)}\right\rangle +\left\langle {A}^{{\prime}{(1)}}{A}^{(2)}{A}^{(3)}\right\rangle \right.\\ \left.+\left\langle {A}^{(1)}{A}^{{\prime}{(2)}}{A}^{{\prime}{(3)}}\right\rangle -\left\langle {A}^{{\prime}{(1)}}{A}^{{\prime}{(2)}}{A}^{{\prime}{(3)}}\right\rangle \right)\le 1.\end{array}$$

For these inequalities, the operator in the anti-diagonal matrix representation has elements of the form,

$$\frac{1}{2}\left(1+{e}^{\iota {k}_{1}{\theta }_{1}}+{e}^{\iota ({k}_{2}{\theta }_{2}+{k}_{3}{\theta }_{3})}-{e}^{\iota ({k}_{1}{\theta }_{1}+{k}_{2}{\theta }_{2}+{k}_{3}{\theta }_{3})}\right).$$

(28)

Consequently, the corresponding absolute values are $2\sqrt{1\pm \sin {\theta }_{1}\sin ({k}_{2}{\theta }_{2}\pm {k}_{3}{\theta }_{3})}$. Clearly, for the maximal quantum violation, the operators A⁽¹⁾ and ${A}^{{\prime}{(1)}}$ must maximally anti-commute, i.e., ${\theta }_{1}=\pm {\!}\frac{\pi }{2}$. However, the maximal quantum violation only requires the sum ${k}_{2}{\theta }_{2}\pm {k}_{3}{\theta }_{3}=\pm {\!}\frac{\pi }{2}$, i.e., the optimal ${A}^{{\prime}{(2)}}$ is defined only in reference to ${A}^{{\prime}{(3)}}$. Clearly, for the maximal quantum violation $2\sqrt{2}$ the shared state must be equivalent to the bipartite maximally entangled state $\left\vert GH{Z}_{2}\right\rangle$. However, these inequalities do not satisfy the strict self-testing criterion as defined in section II, as the optimal local observables are not unique and specified only up-to a mutual relation.

Lastly, we have the equivalence class of the CHSH-like inequalities of the form given below, which correspond to the second inequality listed in Table I of the ref. ⁴⁷,

$$\begin{array}{l}\frac{1}{2}\left(\left\langle {A}^{(1)}{A}^{(2)}{A}^{(3)}\right\rangle +\left\langle {A}^{(1)}{A}^{{\prime}{(2)}}{A}^{(3)}\right\rangle \right.\\ \left.+\left\langle {A}^{{\prime}{(1)}}{A}^{(2)}{A}^{(3)}\right\rangle -\left\langle {A}^{{\prime} {(1)}}{A}^{{\prime}{(2)}}{A}^{(3)}\right\rangle \right)\le 1.\end{array}$$

These inequalities are equivalent to the CHSH or ${{{{\mathcal{M}}}}}_{2}$ inequality for which the proof of Theorem 6 directly applies. The non-zero elements of the anti-diagonal matrix representation of the corresponding Bell operator are of the form,

$$\left(1+{e}^{\iota {k}_{1}{\theta }_{1}}+{e}^{\iota {k}_{2}{\theta }_{2}}-{e}^{\iota ({k}_{1}{\theta }_{1}+{k}_{2}{\theta }_{2})}\right).$$

(29)

The modulo of these values is $2\sqrt{1\pm \sin {\theta }_{1}\sin {\theta }_{2}}$, which implies that for the maximum quantum violation $\sqrt{2}$ the observables for the first pair of parties must maximally anti-commute, i.e., $\pm {\theta }_{1}=\pm {\theta }_{2}=\frac{\pi }{2}$ and shared state must be equivalent to the bipartite maximally entangled state $\left\vert GH{Z}_{2}\right\rangle$.

Apart from the linear inequalities considered here, our proof technique, which relies on the anti-diagonal matrix representation of the Bell operator, is directly applicable to all two settings binary outcome linear (on correlators) multipartite Bell inequalities, either yielding perfect self-testing statements as defined in the beginning of the Results section, or pointing out the impossibility of them, as exemplified above. Next, we obtain self-testing statements using our proof technique for relevant classes of non-linear and complex-valued multipartite Bell expressions.

N party Uffink’s quadratic Bell inequalities and complex Bell expression

As the convex set of biseparable multipartite quantum correlations does not form a polytope, linear inequalities like the Svetlichny inequalities [Eq. (3)] do not form tight, efficient witnesses of genuine multipartite non-locality. On the other hand, the non-linear inequalities such as the Uffink’s family of N ≥ 3 party quadratic (on correlators) inequalities [Eq. (4)] better capture the boundary of the quantum set of biseparable correlations and hence form better witnesses of genuine multipartite quantum non-locality. Here, we use our methodology to obtain self-testing statements for the maximum violation of Uffink’s quadratic Bell inequalities. Specifically, we begin by linearizing Uffink’s N≥3 party quadratic Bell expressions in the following way,

$$\left\langle {{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}\right\rangle ={\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle }^{2}+{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }^{2}=| \left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle \pm \iota \left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle {| }^{2}.$$

(30)

This follows from the simple observation that for any two real numbers ${x}_{1},{x}_{2}\in {\mathbb{R}}$, ${x}_{1}^{2}+{x}_{2}^{2}=| {x}_{1}\pm \iota {x}_{2}{| }^{2}$, and the fact that the N-party MABK operator ${{{{\mathcal{M}}}}}_{N}$ and the N-party complimentary MABK operator ${{{{\mathcal{M}}}}}_{N}^{{\prime} }$ are Hermitian, such that $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle ,\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle \in {\mathbb{R}}$. This linearization reduces our problem to considering a linear but non-Hermition operator, ${\tilde{{{{\mathcal{U}}}}}}_{N}$, of the form,

$$\begin{array}{l}{\tilde{{{{\mathcal{U}}}}}}_{N}\,=\,({{{{\mathcal{M}}}}}_{N}\pm \iota {{{{\mathcal{M}}}}}_{N}^{{\prime} })\\ \qquad=\,\frac{1}{{2}^{\frac{N-1}{2}}}{\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{\bigotimes }\limits_{j=1}^{N}({A}^{(j)}+\iota {A}^{{\prime} (j)}),\end{array}$$

(31)

where the second equality is either satisfied by ${\tilde{{{{\mathcal{U}}}}}}_{N}=({{{{\mathcal{M}}}}}_{N}+\iota {{{{\mathcal{M}}}}}_{N}^{{\prime} })$ or ${\tilde{{{{\mathcal{U}}}}}}_{N}=({{{{\mathcal{M}}}}}_{N}-\iota {{{{\mathcal{M}}}}}_{N}^{{\prime} })$, depending on N, for instance, for N ∈ {2, 5, 6} we have the former while for N ∈ {3, 4, 7} we require the latter form of ${\tilde{{{{\mathcal{U}}}}}}_{N}$. With the linear operator in hand, we can now obtain the self-testing statement for ${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}$, essentially by maximizing the modulo of the possibly complex expectation value of ${\tilde{{{{\mathcal{U}}}}}}_{N}$.

Theorem 7

In order to achieve maximal quantum violation of a N party Uffink’s quadratic inequality, ${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}={2}^{N-1}$, the parties must share a N ≥ 3 qubit GHZ state $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where $\phi (N)\in [-\frac{\pi }{2},\frac{\pi }{2}]$, and perform maximally anti-commuting projective measurements A^(j) = σ_x and ${A}^{{\prime}{(j)}}={\sigma }_{y}$ (up to local isometries).

Proof

From Lemma 2 and Theorem 4, without loss of generality, the local observables of any party ${{{{\mathcal{A}}}}}_{j}$, where j ∈ {1, …, N}, can be taken to be,

$$\begin{array}{l}{A}^{(j)}\,=\,{\sigma }_{x},\\ {A}^{{\prime} {(j)}}\,=\,\cos {\theta }_{j}{\sigma }_{x}+\sin {\theta }_{j}{\sigma }_{y},\end{array}$$

(32)

acting on the effective two-dimensional subspace. This parametrization implies that Uffink’s non-Hermition operator [Eq. (31)], ${\tilde{{{{\mathcal{U}}}}}}_{N}$, has the following anti-diagonal matrix representation,

$${\tilde{{{{\mathcal{U}}}}}}_{N}=\frac{1}{{2}^{\frac{N-1}{2}}}{{{\rm{adiag}}}}\left(\begin{array}{l}{\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}\left(1+\iota {e}^{-\iota {\theta }_{j}}\right.\\ \vdots \\ {\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{\iota {\theta }_{j}})\end{array}\right),$$

(33)

where adiag represents a matrix with non-zero values only on the anti-diagonal. It is easy to see for any combination, $\forall j\in \{1,\ldots ,N\}:{\theta }_{j}=\pm {\!}\frac{\pi }{2}$, one of the anti-diagonal element attains the maximum absolute value of ${2}^{\frac{N-1}{2}}$ while the others vanish.

Since, ${\tilde{{{{\mathcal{U}}}}}}_{N}$ has an anti-diagonal matrix representation, we know that the eigenvectors of such anti-diagonal matrices are of the generic form, $\alpha \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert {i}_{j}\right\rangle +\beta \mathop{\bigotimes }\nolimits_{j=1}^{N}\left\vert \bar{{i}_{j}}\right\rangle$, where i_j ∈ {0, 1} and $\bar{{i}_{j}}=1\oplus {i}_{j}$. Now, taking the expectation value of ${{{{\mathcal{M}}}}}_{N}$ with respect to any one of these states selects the sum of a pair of (equidistant from the top and the bottom) anti-diagonal elements. As each such pair is equivalent to the rest up-to local rotations, we can, without loss of any generality, consider the state, $\left\vert {\psi }_{N}\right\rangle =\alpha {\left\vert 0\right\rangle }^{\otimes N}+\beta {\left\vert 1\right\rangle }^{\otimes N}$, which effectively yields a weighted sum of the top and bottom anti-diagonal elements of the matrix [Eq. (33)],

$$\begin{array}{ll}{{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}\,=| \left\langle {\psi }_{N}\right\vert {\tilde{{{{\mathcal{U}}}}}}_{N}\left\vert {\psi }_{N}\right\rangle | \\ \qquad\, =\,\frac{1}{{2}^{\frac{N-1}{2}}}| \left(\overline{\alpha }{\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})\beta \right.\\ \quad\qquad \,\left.+\,\overline{\beta }{\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{\iota {\theta }_{j}})\alpha \right)| \\ \qquad \,\le \frac{1}{{2}^{\frac{N-1}{2}}}| \alpha | | \beta | \left(| {\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})| \right.\\ \qquad\,\left.+\,| {\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{\iota {\theta }_{j}})| \right),\end{array}$$

(34)

where for the inequality we employed the fact that $\forall \alpha ,\beta \in {\mathbb{C}}:| \alpha +\beta | \le | \alpha | +| \beta |$. Observe that, as ∣α∣² + ∣β∣² = 1, the maximum value of the above expression can only be attained for $| \alpha | =| \beta | =\frac{1}{\sqrt{2}}$, which picks out $\left\vert GH{Z}_{N}\right\rangle$ as the shared state, $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$. We note here that the relative phase $\phi (N)\in [-\frac{\pi }{2},\frac{\pi }{2}]$ is left completely unspecified, a fact that we explore thoroughly at the end of the proof in the following Corollary 7.1. Consequently, we retrieve the following upper bound,

$$\begin{array}{l}| \left\langle {\psi }_{N}\right\vert {\tilde{{{{\mathcal{U}}}}}}_{N}\left\vert {\psi }_{N}\right\rangle | \,\le \frac{1}{{2}^{\frac{N+1}{2}}}| \left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{-\iota {\theta }_{j}})| \right.\\ \qquad\qquad\qquad\quad\left.+\,| {\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}\mathop{{{\Pi }}}\limits_{j = 1}^{N}(1+\iota {e}^{\iota {\theta }_{j}})\right)| .\end{array}$$

(35)

Now, as $| {(\frac{1-\iota }{\sqrt{2}})}^{(N-1){{{\rm{mod}}}}2}| =1$ and $| (1+\iota {e}^{-\iota {\theta }_{j}})| =| 2\sin (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})|$ and $| (1+\iota {e}^{\iota {\theta }_{j}})| =| 2\cos (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})|$, we can further upper bound the above expression as,

$$\begin{array}{ll}| \left\langle {\psi }_{N}\right\vert {\tilde{{{{\mathcal{U}}}}}}_{N}\left\vert {\psi }_{N}\right\rangle | \le &{2}^{\frac{N-1}{2}}\left({{{\Pi }}}_{j = 1}^{N}| \sin \left(\frac{\pi }{4}+\frac{{\theta }_{j}}{2}\right)| \right.\\ &\left.+{{{\Pi }}}_{j = 1}^{N}| \cos \left(\frac{\pi }{4}+\frac{{\theta }_{j}}{2}\right)| \right).\end{array}$$

As, $\forall j:| \sin (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})| \le 1,| \cos (\frac{\pi }{4}+\frac{{\theta }_{j}}{2})| \le 1$, we can further upper bound the above expression by discarding all but three terms corresponding to ∀ i, j, k ∈ {1, …, N}, such that,

$$\begin{array}{ll}| \left\langle {\psi }_{N}\right\vert {\tilde{{{{\mathcal{U}}}}}}_{N}\left\vert {\psi }_{N}\right\rangle | \\ \qquad\le {2}^{\frac{N-1}{2}}\left(\left\vert \sin \left(\frac{2{\theta }_{i}+\pi }{4}\right)\sin \left(\frac{2{\theta }_{j}+\pi }{4}\right)\sin \left(\frac{2{\theta }_{k}+\pi }{4}\right)\right\vert \right.\\ \qquad\quad\left.+\left\vert \cos \left(\frac{2{\theta }_{i}+\pi }{4}\right)\cos \left(\frac{2{\theta }_{j}+\pi }{4}\right)\cos \left(\frac{2{\theta }_{k}+\pi }{4}\right)\right\vert \right)\\ \qquad\le {2}^{\frac{N-1}{2}},\end{array}$$

(36)

where the proof of the second inequality has been deferred to the Supplementary information. In the Supplementary information, we also show that this inequality can only be saturated when ${\theta }_{i}={\theta }_{j}={\theta }_{k}=\frac{\pi }{2}$, i.e., when for each party the local observables maximally anti-commute. Moreover, as these settings maximize a unique pair of equidistant anti-diagonal entries, while the others vanish, the state must be of the form, $\left\vert GH{Z}_{N}\right\rangle \equiv \frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, specified only up to the relative phase ϕ(N), up to auxiliarly degrees of freedom on which the measurements act trivially, and local basis transformations. This further implies that the actual shared state could be of the form $\left\vert GH{Z}_{N}\right\rangle \bigotimes \left\vert {{\Psi }}\right\rangle$ with the arbitrary relative phase ϕ(N) of the GHZ state and the arbitrary state $\left\vert {{\Psi }}\right\rangle$ on auxiliary degrees of freedom which does not contribute to the operational Bell violation and thus is referred to as the junk state.

We would now like to highlight the difference between the self-testing statements for N partite linear MABK inequalities (Theorem 6 and Corollary 6.1) and Uffink’s quadratic Bell inequalities (Theorem 7). Like the linear Bell inequalities, maximal violation of quadratic Bell inequalities fixes the local observables of each party to be maximally anti-commuting, such that without loss of generality they can be taken to be A^(j) = σ_x and ${A}^{{\prime}{(j)}}={\sigma }_{y}$. However, while in the case of N partite linear MABK inequalities fixing the measurements exhausts all freedom up to local isometries and completely specifies the optimal state, on the other hand, the maximal violation of Uffink’s quadratic inequalities does not uniquely specifies the optimal state. Specifically, the maximal violation of Uffink’s quadratic inequalities can be attained with $\left\vert GHZ(\phi (N))\right\rangle$ where the relative phase ϕ(N) could take any value in $[-\frac{\pi }{2},\frac{\pi }{2}]$. Hence, Uffink’s quadratic inequalities do not strictly self-test. Below we show that strict self-testing statements can nevertheless be obtained for the complex-valued N partite Bell expression corresponding to the expectation value of Uffink’s non-Hermitian operator $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle$[Eq. (31)] whenever the corresponding Uffink’s quadratic Bell inequalities is maximally violated.

Until now, we have used our methodology to obtain self-testing statements for real valued linear and qaudratic (on correlators) Bell expressions. We now discuss the case when our Bell expression takes complex values. Specifically, in the following Corollary, we obtain self-testing statements for the complex-valued Bell expression corresponding to the complex expectation value of $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle$, where the operator ${\tilde{{{{\mathcal{U}}}}}}_{N}$ is defined in Eq. (31), using our methodology.

Corollary 7.1

In order to achieve extremal quantum value of the complex-valued Bell expression, $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle =({{{{\mathcal{M}}}}}_{N}\pm \iota {{{{\mathcal{M}}}}}_{N}^{{\prime} })$, such that $| \left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle | ={2}^{\frac{N-1}{2}}$, the parties must share a N ≥ 3 qubit GHZ state $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where $\phi (N)={{{\rm{arccot}}}}\left(\frac{\left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{N}}}}}\right\rangle }{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }\right)$ when N is odd, $\phi (N)={{{\rm{arccot}}}}\left(\frac{\left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{N}}}}}\right\rangle }{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }\right)-\frac{\pi }{4}$ when N is even and perform maximally anti-commuting projective measurements A^(j) = σ_x and ${A}^{{\prime} {(j)}}={\sigma }_{y}$ (up to local isometries).

Proof

From Theorem 7, we know that the maximal quantum value of ${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}=| \left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle {| }^{2}={2}^{N-1}$, self-tests the state to be maximally entangled N partite GHZ state, $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where the relative phase ϕ(N) can be chosen arbitrarily. However, here we show that this relative phase ϕ(N) can still be operationally determined from the complex-valued Bell expression,

$$\begin{array}{r}\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle =\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle \pm \iota \left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle ,\end{array}$$

(37)

where $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle$ and $\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle$ are real valued complementary MABK Bell expressions for N parties, such that $| \left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle |$ is ${2}^{\frac{N-1}{2}}$. We know that $| \left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle | ={2}^{\frac{N-1}{2}}$ implies that the local observables of each party can always be taken to be A^(j) = σ_x, ${A}^{{\prime}{(j)}}={\sigma }_{y}$, such that the operator ${\tilde{{{{\mathcal{U}}}}}}_{N}$ has the matrix representation [Eq. (33)]. Consequently,

$$\begin{array}{l}\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle \,=\,\left\langle GH{Z}_{N}\right\vert {\tilde{{{{\mathcal{U}}}}}}_{N}\left\vert GH{Z}_{N}\right\rangle \\ \qquad\quad\,=\,{2}^{\frac{N+1}{2}}\left(\overline{\alpha }{(\frac{1-\iota }{\sqrt{2}})}^{(N-1){{{\rm{mod}}}}2}\beta \right)\end{array}$$

(38)

Up to experimentally indeterminable global phase, we can always take $\alpha =\frac{1}{\sqrt{2}}$ and $\beta =\frac{{e}^{\iota \phi }}{\sqrt{2}}$, such that Eq. (38) is simplified to,

$$\begin{array}{l}\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle \,=\,{2}^{\frac{N-1}{2}}\left({\left(\frac{1-\iota }{\sqrt{2}}\right)}^{(N-1){{{\rm{mod}}}}2}{e}^{\iota \phi }\right)\\ \qquad\quad=\,\left\{\begin{array}{l}{2}^{\frac{N-1}{2}}{e}^{\iota \phi },\,{{{\rm{iff}}}}\,N\,{{{\rm{is}}}}\,{{{\rm{odd}}}},\quad \\ {2}^{\frac{N-1}{2}}{e}^{\iota (\phi -\frac{\pi }{4})},\,{{{\rm{else}}}}.\quad \end{array}\right.\end{array}$$

(39)

Next, with the aid of Eqs. (37) and (39), we can finally uniquely specify the relative phase ϕ(N) operationally. When $| \left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle | ={2}^{\frac{N-1}{2}}$ and the number of parties, N, is odd, the relative phase ϕ(N), must be precisely ${{{\rm{arccot}}}}\left(\frac{\left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{N}}}}}\right\rangle }{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }\right)$, else $\phi (N)={{{\rm{arccot}}}}\left(\frac{\left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{N}}}}}\right\rangle }{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }\right)-\frac{\pi }{4}$ up to local isometries.

We note here that $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle$, although complex, is an operational quantity, i.e., just like the value of linear Bell expressions, it can be directly estimated from the experimental statistics. Corollary 7.1 allows us to infer the relative phase ϕ(N) of the N ≥ 3 qubit GHZ state from $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle$. This fact is illustrated in Fig. 2.

Fig. 2: Self-testing of the relative phase ϕ(N).

This graphic schematically captures the self-testing statements for N partite Uffink’s quadratic Bell inequalities (Theorem 7), as well as the self-testing statements for the complex-valued Bell expressions corresponding to the mean value of Uffink’s non-Hermitian operator $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle$ (Corollary 7.1). The figure depicts the complex plane on which the complex number $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle =\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle \pm \iota \left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle$ lies, where $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle$ is plotted on the real axis while $\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle$ is plotted on the imaginary axis. The dark blue arc represents the boundary of the quantum set of correlations ${{{\mathcal{Q}}}}$ characterized by the maximum violation of N partite Uffink’s quadratic Bell inequalities, ${{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}}=| \left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle {| }^{2}={2}^{N-1}$. Crucially, for all points on the dark blue arc, Theorem 7 implies that the local observables of each party can be taken to be A^(j) = σ_x and ${A}^{{\prime} {(j)}}={\sigma }_{y}$, and the state to be maximally entangled N partite GHZ state, $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where the relative phase ϕ(N) can be chosen arbitrarily (up to local isometries). However, using Corollary 7.1, even the relative phase can be uniquely identified by the observed value of $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle$ if it lies on this arc. To exemplify this, we plot the specific case of $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle =\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle \pm \iota \left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle ={2}^{\frac{N-2}{2}}{e}^{\iota \frac{\pi }{3}}$ (light blue arrow), which uniquely specifies the relative phase to be $\phi (N)={{{\rm{arccot}}}}\left(\frac{\left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{N}}}}}\right\rangle }{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }\right)=\frac{\pi }{3}$ when N is odd, and $\phi (N)={{{\rm{arccot}}}}\left(\frac{\left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{N}}}}}\right\rangle }{\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }\right)-\frac{\pi }{4}=\frac{\pi }{12}$ when N is even.

Robust self-testing

The criterion for self-testing of a Bell inequality used in this work relies strongly on the assumption that the considered Bell expression attains its maximal value. However, in real experiments, this assumption cannot be fulfilled due to various experimental imperfections. Therefore, the self-testing statements must be made robust.

To make the self-testing statements obtained in this work robust, one can use the numerical SWAP method, which utilizes the Navascues-Pironio-Acin hierarchy to obtain bounds on the closeness (fidelity) of the experimental measurements and the shared state to the ideal self-testing measurements and state. Here we detail the technique for bounding the fidelity between the actual state and the reference self-testing state; the same can be applied to retrieve corresponding bounds for the measurements. The main idea of this technique relies on the notion of local isometries, which map the actual physical state $\left\vert \bar{\psi }\right\rangle$ to our reference self-testing state $\left\vert \psi \right\rangle$ and a junk state $\left\vert {{\Psi }}\right\rangle$ on local auxiliary systems. In most of the self-testing cases, these local isometries act as partial SWAP gates, essentially swapping the actual physical state $\left\vert \bar{\psi }\right\rangle$ with the state ${\left\vert 0\right\rangle }^{\otimes N}$ of the registers, such that the final state of the registers corresponds to the reference self-testing state $\left\vert \psi \right\rangle$. It is often instructive to visualize the action of these local isometries as a SWAP circuit, which only depends on the self-testing measurements. The particulars of such a SWAP circuit, specifically those of the local isometries, enable us to express the fidelity, ${{{{\mathcal{F}}}}}_{n}=\left\langle \psi \right\vert {\rho }_{SWAP}({{{\Gamma }}}_{n})\left\vert \psi \right\rangle$, of the final state of the register ρ_SWAP (Γ_n) with the target state $\left\vert \psi \right\rangle$, as a function of the entries of the necessarily positive semi-definite NPA moment matrix Γ_n of level $n\in {\mathbb{N}}$, as well as of the target self-testing state $\left\vert \psi \right\rangle$. As some of the entries of the moment matrix Γ_n correspond to experimental statistics, such as ${[{{{\Gamma }}}_{n}]}_{{\bar{A}}^{(1)},{\bar{A}}^{(2)}}=\left\langle \bar{\psi }\right\vert {\bar{A}}^{(1)}{\bar{A}}^{(2)}\left\vert \bar{\psi }\right\rangle$, the behavioral preconditions of a self-testing statement translate to linear constraints on the entries of the moment matrix Γ_n. Given a target self-testing state $\left\vert \psi \right\rangle$ and solving the consequent semi-definite minimization program with the fidelity, ${{{{\mathcal{F}}}}}_{n}=\left\langle \psi \right\vert {\rho }_{SWAP}({{{\Gamma }}}_{n})\left\vert \psi \right\rangle$ as the linear objective function, retrieves a converging sequence of lower bounds, ${{{{\mathcal{F}}}}}_{1}\le {{{{\mathcal{F}}}}}_{2}\ldots {{{{\mathcal{F}}}}}_{n}$ such that ${{{{\mathcal{F}}}}}_{n\to \infty }={{{\mathcal{F}}}}$, where ${{{\mathcal{F}}}}$ is the quantum fidelity.

In Fig. 3, we depict the SWAP circuit corresponding to the N party self-testing statements obtained in this work for MABK inequalities (Theorem 6), complimentary MABK inequalities (Corollary 6.1), Uffink’s quadratic inequalities (Theorem 7) and Uffink’s complex-valued Bell expressions (Corollary 7.1). As the self-testing measurements for all of these cases are the same, i.e., A^(j) = σ_x and ${A}^{{\prime} {(j)}}={\sigma }_{y}$, the circuit in Fig. 3 effectively swaps the actual state $\left\vert {\bar{\psi }}_{N}\right\rangle$ (which attains the respective preconditions of these self-testing statements) with the state ${\left\vert 0\right\rangle }^{\otimes N}$ of the registers, such that the final state of the registers corresponds to their respective self-testing maximally entangled N partite GHZ state, $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$. This, in turn, allows us to retrieve a converging sequence of lower bounds on the fidelity, ${{{{\mathcal{F}}}}}_{n}=\left\langle GH{Z}_{N}\right\vert {\rho }_{SWAP}({{{\Gamma }}}_{n})\left\vert GH{Z}_{N}\right\rangle$, in the aforementioned fashion.

Fig. 3: Swap circuit.

This graphic represents the partial SWAP gate isometry used to self-test maximally entangled N partite GHZ state $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$. After the application of the circuit, the $\left\vert GH{Z}_{N}\right\rangle$ state is extracted from the actual experimental state $\left\vert {\tilde{\psi }}_{N}\right\rangle$ to the ancillary qubits. Here, H denotes a Hadamard gate, and X₁, Y₁, X₂, Y₂, …X_N, Y_N are the operators which act analogously to σ_x, σ_y on the actual state $\left\vert {\tilde{\psi }}_{N}\right\rangle$. As the circuit only depends on the self-testing measurements, this circuit works for the N partite self-testing statements obtained in this work, namely, the self-testing statements for MABK inequalities (Theorem 6), complimentary MABK inequalities (Corollary 6.1), Uffink’s quadratic inequalities (Theorem 7) and Uffink’s complex-valued Bell expressions (Corollary 7.1). As the self-testing measurements for all of these cases are the same, i.e., A^(j) = σ_x and ${A}^{{\prime} {(j)}}={\sigma }_{y}$, the circuit SWAPs the actual state $\left\vert {\bar{\psi }}_{N}\right\rangle$ (which attains the respective preconditions of these self-testing statements) with the state ${\left\vert 0\right\rangle }^{\otimes N}$ of the registers, such that the final state of the registers corresponds to their respective self-testing maximally entangled N partite GHZ state.

As the resultant semi-definite programs, although straightforward to implement^22,23, are too computationally hard to solve efficiently without additional symmetry-based simplifications, we leave this as a future direction.

We now highlight the advantage of Uffink’s quadratic Bell inequalities and Uffink’s complex-valued Bell expressions over the linear MABK inequalities for robust self-testing in noisy experimental scenarios. Heuristically, as Uffink’s quadratic Bell inequalities and Uffink’s complex Bell expressions take two experimentally observable quantities into account, namely, the value of linear MABK inequality, $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle$, as well as the value of linear complementary MABK inequality $\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle$, they provide more accurate robust self-testing than when the latter are considered on their own.

Specifically, consider an experiment E aimed at robust self-testing of the N qubit GHZ state using N party MABK Bell expression, $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle$. Suppose that the experiment yields the value ${\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle }_{E}={2}^{\frac{N-1}{2}}-\epsilon$, the fidelity ${{{{\mathcal{F}}}}}_{1}$ of the experimental state with the N qubit GHZ state optimal for $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle$ (Theorem 6) is proportional to ${2}^{\frac{N-1}{2}}-\epsilon$. However, the experimental imperfections will inevitably yield experimental behavior for which ${\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }_{E}\ne 0$. Consequently, the experimental behavior will always be closer to the extremal point which attains $\left\langle {\tilde{{{{\mathcal{U}}}}}}_{N}\right\rangle =\frac{{2}^{\frac{N-1}{2}}}{\sqrt{{({{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}})}_{E}}}({\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle }_{E}\pm \iota {\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }_{E})$ as compared to the extremal point which attains $\left\langle {{{{\mathcal{M}}}}}_{N}\right\rangle ={2}^{\frac{N-1}{2}}$ and $\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle =0$. Hence, the fidelity of the experimental state with the target GHZ state $\left\vert GH{Z}_{N}\right\rangle$ which realizes this extremal point (from Corollary 7.1) will yield a fidelity ${{{{\mathcal{F}}}}}_{2}$ proportional to $\sqrt{{({{{{\mathcal{U}}}}}_{N}^{{{{\mathcal{M}}}}})}_{E}}=\sqrt{{({2}^{\frac{N-1}{2}}-\epsilon )}^{2}+{({\left\langle {{{{\mathcal{M}}}}}_{N}^{{\prime} }\right\rangle }_{E})}^{2}}$, such that, ${{{{\mathcal{F}}}}}_{2} > {{{{\mathcal{F}}}}}_{1}$. Hence, in general taking into account, Uffink’s quadratic and complex-valued Bell expressions provide for a more accurate and robust DI self-testing of the N qubit GHZ state as compared to the MABK inequalities, especially in cases when the relative phase is irrelevant to the application and could be arbitrary.

Consequently, Uffink’s quadratic and complex-valued Bell expressions provide for a more accurate and robust DI characterization of quantum systems in multipartite Bell scenarios as compared to the MABK inequalities.

Discussions

Quantum correlations that violate Bell inequalities can certify the shared entangled state and local measurements in an entirely device-independent manner. This feature of quantum non-local correlations is referred to as self-testing. In this work, we presented a simple and broadly applicable proof technique to obtain self-testing statements for the maximum quantum violation of a large relevant class of multipartite (involving an arbitrary number N of spatially separated parties) Bell inequalities. Unlike the relatively straightforward bipartite Bell scenarios, the multipartite scenarios are substantially richer in complexity owing to the various types of multipartite non-locality.

The traditionally employed sum-of-squares-like proof techniques rely on the Bell inequality’s specific structure and the hermiticity of the corresponding Bell operator. Moreover, we recall here that finding the sum-of-squares decomposition for a linear Bell expression is the semi-definite programming dual of finding the maximum quantum value of the Bell expression, which in turn can be cast as an instance of the moment-based formulation Navascues-Pironio-Acin hierarchy of semi-definite programming relaxations^48,49. It follows from this semi-definite programming duality that the level of the moment-based Navascues-Pironio-Acin hierarchy required for saturation of the maximal quantum value of a Bell expression corresponds to the degree of the polynomials in the sufficient sum-of-squares decomposition of the corresponding Bell operator. It is also easy to see that the minimum level $\lceil \frac{N}{2}\rceil$ of the moment-based Navascues-Pironio-Acin hierarchy degree required for the saturation of N party Bell inequalities, such as the MABK and the complimentary MABK family of Bell inequalities, increases with N, and so does the maximum degree of the polynomials in the corresponding sum-of-squares decomposition. Consequently, finding sum-of-squares decomposition becomes increasingly arduous for a large number N of spatially separated parties.

Although the Sum-of-Squares decomposition is applicable to any Bell scenario, more often than not, finding it can be challenging. In contrast, the technique presented in this paper offers a more state-forward approach. It is applicable to binary input and output Bell scenarios with an arbitrary number of spatially separated parties (N). It can derive self-testing statements for any Bell inequality in such Bell scenarios, as long as the associated Bell operator has an anti-diagonal matrix representation. In “Results: Characterizing local observables”, we show that the observables of each party in two-setting binary outcome multipartite Bell scenarios can always be simultaneously represented as anti-diagonal matrices (Theorem 4). Consequently, in such scenarios, the Hermitian Bell operators corresponding to all Bell inequalities composed exclusively of N party correlators also have an anti-diagonal matrix representation. In “Results: Self-testing statements for multipartite inequalities”, to demonstrate our proof technique, we obtain proofs of self-testing statements for the MABK family of N party inequalities (Theorem 6) (This constitutes a reproduction of the self-testing statements for MABK inequalities from ref. ³⁹, and hence serves as a preliminary certification of our proof technique.), followed by self-testing statements for the complimentary N party MABK inequalities (Corollary 6.1) and tripartite WWWŻB inequalities (“Results: Tripartite WWWŻB inequalities”). While the former self-testing statements demonstrate the relative simplicity and scalability (in the number of parties N) of our proof technique and serve as reliable benchmarks, the latter self-testing statements serve to exemplify all possible exceptions to perfect self-testing statements such as non-unique optimal states or observables, and non-anticommuting pairs of optimal measurements.

To further demonstrate the versatility of our proof technique which relies only on the anti-diagonal matrix representation of the Bell operator and not even on its hermiticity, we obtain self-testing statements for Uffink’s family of quadratic Bell inequalities (Theorem 7), as well as for the novel complex-valued Uffink’s Bell expressions with corresponding non-Hermitian Bell operators (Corollary 7.1). As these quadratic and complex Bell expressions do not allow for sum-of-squares-like self-testing techniques, which rely on the linearity of the Bell expressions and on the hermiticity of the associated Bell operators, the self-testing statements obtained here form distinguishing applications of our proof technique.

One of the salient features of the multipartite self-testing statements obtained in this work, namely, for maximum quantum violation of MABK inequalities (Theorem 6), complimentary MABK inequalities (Corollary 6.1), Uffink’s quadratic inequalities (Theorem 7) and extremal quantum values of Uffink’s complex-valued Bell expressions (Corollary 7.1), is that they all uniquely single-out anti-commuting binary outcome observables for each party, which, without loss of generality, can be taken to be σ_x and σ_y, up to local isometries. On the other hand, these self-testing statements also pick out the maximally entangled N partite GHZ state $\left\vert GH{Z}_{N}\right\rangle =\frac{1}{\sqrt{2}}({\left\vert 0\right\rangle }^{\otimes N}+{e}^{\iota \phi (N)}{\left\vert 1\right\rangle }^{\otimes N})$, where $\phi (N)\in [-\frac{\pi }{2},\frac{\pi }{2}]$ is the relative phase. However, while the self-testing statements for the MABK and the complementary MABK inequalities uniquely specify ϕ(N), the self-testing statements for Uffink’s quadratic Bell inequalities do not uniquely specify the phase ϕ(N). These observations lead to the self-testing statements (Corollary 7.1) for the extremal values of the novel Uffink’s complex-valued Bell expressions, which effectively summarize the former statements. Specifically, fixing the local observables of each party to be σ_x and σ_y, Corollary 7.1 brings forth the one-to-one correspondence between the experimentally accessible extremal values of Uffink’s complex-valued Bell expressions and the relative phase ϕ(N) of the N partite GHZ state, essentially demonstrating the operational relevance of the latter.

The N-party MABK inequalities [Eq. (2)] form efficient witnesses of genuine N-partite non-locality and entanglement and hence find applications in tasks that require the participation of all parties, i.e., the tasks in which no subset of the parties can succeed without the others⁴⁷, for example, quantum secret sharing⁵⁰, social welfare games⁵¹, DI randomness generation and expansion⁵², and conference key distribution schemes^53,54. The advantage of the MABK inequalities over the other inequalities in N-partite DI information processing and cryptography task springs from its permutational symmetry, which does not privilege one party at the expense of the other parties. Uffink’s quadratic inequalities [Eq. (4)] and complex-valued Bell expression [Eq. (31)] also retain this permutational symmetry while being strictly better at witnessing genuine N-partite non-locality and entanglement. The DI information processing and cryptographic applications are essentially fueled by the characterization of the quantum devices, enabled by the values of respective Bell expressions, as exemplified by the self-testing statements presented in this work. Consequently, as Uffink’s quadratic inequalities and complex-valued Bell expression allow for a more accurate and robust certification of quantum devices, using them instead of MABK in DI applications can only benefit the respective performance.

Note added: During the preparation of the current work, we have become aware of ref. ⁵⁵. While it presents similar results, our proof technique, which constitutes the main conceptual contribution of this work, is substantially different from their proof technique. In particular, the key contrasting feature of our proof technique is its applicability to non-linear Bell inequalities.