Introduction

Noisy intermediate scale quantum (NISQ) devices, although imperfect, can have an advantage over classical computers at certain tasks1,2. Especially, analog quantum simulators (AQS), have advanced drastically over the last decade and can now tackle problems that are hard to solve for classical computers3,4. This is largely owed to the simplicity of their concept: in contrast to gate-based quantum computing, analog devices directly emulate a Hamiltonian of interest and thereby mimic all of its properties. Since they lack the flexibility and accuracy of a digital quantum computer, AQS are best suited to study universal effects, which are more or less resistant to small perturbations1. Therefore, open quantum systems are an appealing target for analog simulation, particularly, because they are also hard to model with both classical5 and gate-based quantum computers6.

One such system is the multistate Landau-Zener model. It describes the interaction of an excitation at a time-dependent energy level with at least one other state or mode spectrum. Examples are the underlying Hamiltonian models for molecular collisions7 and chemical reaction dynamics8. It is also ubiquitous in many artificial quantum devices, which have generated a broad research interest in recent years. In experimental studies on super-9,10,11 and semiconducting qubits12,13, or nitrogen-vacancy centers in diamond14,15 a Mach-Zehnder-like interference effect was exploited for quantum state preparations. The transient dynamics of the Landau-Zener model was also studied experimentally11,16,17,18, albeit only for two-state systems. In contrast, various theoretical works on the topic focus on the more complex multistate Landau-Zener model19,20,21,22. In particular, the time evolution of the system’s state and its dependence on the mode spectrum are of great interest there.

In this work, we study the transient dynamics of the multistate Landau-Zener model of a superconducting quantum circuit. A tunable transmon qubit is used to realize a time-dependent energy state. An artificial spectral environment is formed by four harmonic oscillators which are implemented as lumped element microwave resonators. We study the time evolution of the system as a function of the Landau-Zener velocity v, i.e., the speed at which the energy level separation bypasses the narrow spectral bath. In circuit, we are not limited to exciting the system via the qubit, but can also pump the harmonic modes directly. This allows us to investigate the qubit’s time evolution for various initial states, and, in particular, as a function of the average photon number in the system. In our experiments, we observe coherent oscillations of the qubit population. For low average photon numbers, we compare our findings with numerical QuTiP simulations. For a strongly driven bosonic bath the transient dynamics gradually changes from a coherent oscillating to an adiabatic transition of the mode ensemble. We identify the \(\sqrt{n}\)-enhancement of the coupling strength23 between the qubit and resonators with the number of photons n in the system as the underlying cause.

Results

Implementation of the simulator

The Hamiltonian of the multistate Landau-Zener model reads

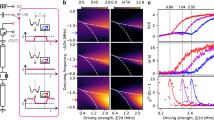
$$\frac{{\hat{H}}_{{\rm{LZ}}}}{\hslash}=\frac{\nu t}{2}{\hat{\sigma }}_{z}+\mathop{\sum}\limits_{n}\left({\omega }_{n}{\hat{a}}_{n}^{{\dagger} }{\hat{a}}_{n}+{g}_{n}{\hat{\sigma }}_{x}\left({\hat{a}}_{n}^{{\dagger} }+{\hat{a}}_{n}\right)\right),$$
(1)

where \({\hat{\sigma }}_{x,z}\) are the Pauli-Operators of a two-level system with a time-dependent frequency of vt, \({\hat{a}}_{n}\) is the annihilation operator of the nth bosonic mode with a frequency of ωn, and gn is the coupling strength of the nth bosonic mode to the two-level system. An implementation of this system with superconducting devices is straightforward, due to their tailored functionality and the good control over all circuit parameters. Figure 1a displays a micrograph of our simulation device. We use a tunable transmon qubit to approximate the two level system with a time-dependent energy transition, i.e., the leading term in the Hamiltonian. An impedance matched flux bias line coupled to the SQUID of the qubit enables fast control of the qubit frequency. At the working point, the qubit is tunable over a frequency range of up to ~ 400 MHz. This is partially limited by the bias tee employed to combine AC and DC current biases, see Supplementary Methods. The qubit has an anharmonicity of α/2π = 241 MHz and a rather large decoherence rate of Γ2 = 5 μs−1, which is not limited by the energy decay rate Γ1 = 0.2 μs−1. Due to the steep qubit dispersion at the operation point, flux noise is a likely limiting factor. The bosonic modes in the model are emulated by several lumped element microwave resonators with frequencies situated at around 5.5 GHz and capacitively coupled to the qubit. Experimentally, we find that only four of the five resonators interact with the qubit, see Supplementary Methods for detailed information. Qubit readout is performed dispersively utilizing a λ/4-stripline resonator with a resonance frequency of 6.86 GHz.24,25. Qubit gates are applied via a dedicated drive line. An additional input line coupled to the bath resonators allows for a direct spectroscopy of their transition frequencies and can be exploited in time domain experiments to directly apply microwave pulses to the bosonic modes.

Fig. 1: Characterization of the quantum simulator and simulation scheme.
figure 1

a Micrograph of the simulation device. An ensemble of five lumped element resonators (orange) with a dedicated input line (red) is coupled capacitively to a transmon qubit (blue). We achieve fast tunability using an impedance matched flux bias line (cyan) coupled to the SQUID of the qubit. DC and AC current biases, respectively generated by a current source and AWG, are combined with a bias tee. Qubit gates are admitted via a dedicated drive port (yellow). A λ/4-resonator (purple) is employed for the dispersive measurement of the qubit state. b Two-tone spectroscopy of the avoided level crossings between the first qubit transition and bosonic modes. The coupling coefficients are extracted from a fit to the mode spectrum, see black dashed lines. They are in the same order as the frequency spacing between the harmonic modes. c At the start of the quantum simulation, the qubit frequency ωq (blue line) is tuned to ωi. Here, the system’s initial state is prepared, shown for a π-pulse to the qubit. Thereafter follows a linear increase of the qubit frequency for a certain time t. We stop the qubit frequency sweep by returning the qubit to ωi, where dispersive state readout is performed. The qubit population along the trajectory is determined by repeating this process for different values of t up to a maximum rise time trise, where ωq = ωf.

Full size image

Figure 1b shows a two-tone measurement of the coupled multi-mode system, in the single-photon manifold. Here, the qubit frequency is tuned in and out of resonance with the bosonic modes via a DC current bias applied to the flux coil. Thereby, several avoided level crossings are revealed, which we employ to extract the coupling coefficients between the qubit and resonators. The frequency spacing of the bosonic modes is of the same order as their coupling strength to the qubit. The extracted device parameters are summarized in Supplementary Table 1 and are also employed in the numerical simulation of the system.

The Landau-Zener model is directly emulated by the quantum hardware. Therefore, no complex driving scheme is needed to run the simulation. The analog simulation follows the simple algorithm of system state preparation, free time evolution as the qubit frequency is increased, and finally qubit state readout, see Fig. 1c. Due to experimental constraints, the qubit is initially flux biased to ωq = ωi rather than to zero-frequency, approximately 200 MHz below the bosonic modes’ transitions. The Landau-Zener velocity is given by v = (ωf − ωi)/trise, where the final qubit frequency ωf is reached after the time trise. In the experiment, both ωi and ωf are measured quantities, while trise is adjusted by the arbitrary waveform generator (AWG) used to tune the qubit frequency ωq. We determine the qubit population at several time steps along this trajectory. For state readout, the qubit is returned to ωi, halting the time evolution. The time resolution is limited to 1 ns by the AWG generating the tuning pulse.

Multi-mode Landau-Zener model

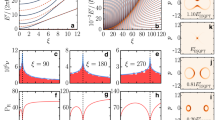
For the first experiment discussed in this work, we prepare the system in the first excited state, i.e., the excited state of the qubit, by applying a weak π-pulse ( ~ 140 ns length). Thereby, we make sure that the time development is dominated by the dynamics of the Landau-Zener model, rather than rotations of the qubit state stemming from the preparation in a system non-eigenstate. Figure 2a displays the results of our analog quantum simulation, side by side with numerical QuTiP simulations26,27, see Fig. 2b. In the numerical simulations, we truncate the bosonic modes to the first two Fock states and omit energy relaxation and decoherence of the system.

Fig. 2: Transient dynamics in the multistate Landau-Zener model with an initially excited qubit.
figure 2

a Quantum and b numerical simulation of qubit population as a function of the qubit frequency ωq(t) = ωi + vt and rise time trise = (ωq − ωf)/v with the Landau-Zener velocity v. During the transition of the resonator ensemble (frequencies indicated by dashed orange lines), the population of the initially excited qubit undergoes a steep drop, followed by coherent oscillations with diminishing amplitude. This is especially apparent for long rise times. c Quantitative comparison of the experiment (dots) and numerical simulation (lines) for different rise times, indicated by blue arrows in b. Shaded areas indicate the standard deviation of the qubit population. Neighboring traces are shifted by 1 to improve visibility. d Final qubit population as a function of the rise time trise. Oscillations persist in measurement and simulation, nevertheless, the final qubit population is well approximated by the generalized Landau-Zener formula, see Eq. (2).

Full size image

Qualitatively, we observe that, independent of the rise time, the qubit retains its excited state population until it reaches the resonator ensemble. After scattering on the bosonic modes, coherent oscillations of the qubit population emerge. The oscillation frequency is proportional to the energy difference of the qubit and bath states9. Therefore, it is independent of the coupling coefficients and solely depends on the velocity v and increases with time. The oscillation amplitude decreases with time, i.e., for increasing qubit frequency. We emphasize that this effect is not introduced by the limited life-, and coherence time of the simulation device. Rather, it is how the system converges to a static state achieved in the limit of trise → ∞. We confirm the good quantitative agreement of numerics and experiment in a trace-wise comparison for several different rise times, see Fig. 2c. In the experiment, we have to account for a small offset of 5.2 ns to trise, see methods section, likely caused by a distortion of the tuning pulse after traversing the microwave lines to the sample.

Figure 2d displays the final qubit population as a function of rise time, in good agreement with numerical simulations. A potential cause of the overshoot of the qubit population for short rise times is constructive Mach-Zehnder interference9, which can occur due to the finite time needed to return the qubit frequency to ωi. We also compare our results with the generalized Landau-Zener formula28,29,30, which predicts a qubit population of

$${P}_{\rm{q}}=\mathop{\prod}\limits_{n}\exp \left(-\frac{2\pi }{\nu}{g}_{n}^{2}\right).$$
(2)

for trise → ∞. Each avoided level crossing can be interpreted as a beamsplitter for incoming photons9. Therefore, multiple crossings consecutively reduce the probability of the photon remaining in the qubit. Apart from the remnants of coherent oscillations in the measurement, our data are in agreement with the analytical formula. As predicted, the qubit remains in the excited state for trise → 0, with the final state exponentially approaching the ground state in the adiabatic limit of trise → ∞.

Excited ensemble

Due to the dedicated drive line for the resonators, we can also pump the bosonic modes, rather than exciting the qubit. Thereby, their roles are reversed and the qubit, this time initially in the ground state, acquires (a fraction of) a photon from the populated mode during the transit. Since we cannot easily prepare the resonators in a Fock state, we apply a short drive pulse to one of the resonators. Thereby, it is prepared in a superposition state including higher levels, where the average photon number depends on the duration tp of the pump pulse. Since tp is lower than the resonators’ decay rates κ across all presented experiments, the pump does not result in a coherent state in the excited oscillator.

Figure 3 displays the quantum (a–d) and numerical simulation (e–h) of the qubit population during the transition of resonator ensemble, one of which is excited. The pump pulse duration in the presented experiments was chosen as tp = 80 ns. In the numerical simulation, the bosonic mode was initialized in a one-photon Fock state to reduce the complexity of the calculation. Once again, coherent oscillations of the qubit population emerge after its frequency traverses the bath. Here, the amplitude of the oscillations strongly depends on the initial state of the system. This is particularly clear in the picture of a chain of beamsplitters, where the survival probability of an injected photon increases when injected at a later stage. Furthermore it also explains the shift of the center of mass of the oscillation towards larger trise for a higher frequency of the initially excited resonator.

Fig. 3: Qubit population dynamics with an excited resonator mode.
figure 3

The qubit starts in the ground state and transitions the bosonic modes, one of which is excited. Each column of the panels corresponds to a different initial state, where the resonators are excited in ascending order (bi for the ith resonator). In the experiment a–d, a single resonator is prepared in a state with a low average population. e–h QuTiP simulation of the dynamics (compare a to e, etc.). We find coherent oscillations of the qubit population. As expected from a series of beamsplitters, the amplitude depends strongly on the excited resonator, i.e., where the photon is injected in the beamsplitter setup. i Transient dynamics for trise = 50 ns for a larger average photon number in resonator b1. Shaded areas indicate the standard deviation of the qubit population. Neighboring traces are shifted by 0.25 to improve visibility. By increasing the duration tp (shown for 250, 300, 400, 550, and 750 ns) of the pump pulse higher Fock states contribute to the dynamics of the system. The \(\sqrt{n}\)-scaling of the effective coupling strength between qubit and resonator with the photon number n of the respective Fock state increases the Landau-Zener tunneling probability, see Eq. (2). Initially, this results in a greater oscillation amplitude and a larger final value of the qubit population after the transit, but gradually shifts towards an adiabatic transition. For tp = 750 ns, the coherent oscillations of the qubit population are fully suppressed and the qubit is (approximately) in the excited state upon reaching ωf.

Full size image

What happens if we now increase the average photon number in the excited resonator? Figure 3i shows the qubit population in dependence on the average photon number 〈n〉 in the lowest frequency resonator b1 and for trise = 50 ns. Here, we change 〈n〉 by varying the duration tp of the pump tone. Comparing with Fig. 3a, a higher population of the resonator initially leads to more pronounced oscillations with a larger amplitude. For very long pump tones the behavior changes to an increasingly adiabatic transition of the avoided level crossing. In the Jaynes-Cummings model, which is the basis of our simulator, the matrix element between a Fock state with photon number n and the qubit ground state scales with \(\sqrt{n}\)23. The Landau-Zener tunneling probability scales with the square of this matrix element, see Eq. (2), which in turn corresponds to a faster (smaller Landau-Zener velocity v), more adiabatic transit. A direct comparison with numerical simulations proves challenging, due to the complex initial state of the pumped resonator and the large Hilbert space of the system. However, we can qualitatively reproduce the time evolution of the qubit population in a drastically simplified version of the system, comprising only two resonators, see Supplementary Discussion.

Discussion

In this work, we experimentally investigated the time evolution of the multistate Landau-Zener model using a superconducting quantum simulator. The focus of this study was the transient dynamics of the qubit population in the vicinity of several bath resonators forming a spectral environment. By changing the Landau-Zener velocity v and the initial state of the system we observed coherent oscillations of the qubit population, which subdue towards large v where the transition becomes adiabatic. In contrast to previous studies of the model, our simulator allows for a preparation of higher excited states of the participating bosonic modes. For a larger average photon number 〈n〉, the transit of the avoided level crossings gradually becomes adiabatic, which is the result of an effectively larger coupling strength \(g\propto \sqrt{n}\) between the qubit and the nth Fock state of the excited resonator. Throughout the paper, we validate the results of the quantum experiments with numerical QuTiP simulations. Our implementation of an engineered spectral environment inspires future efforts towards emulating the dynamics of open quantum systems with superconducting quantum circuits. For example, it offers a promising approach to realize a quantum simulator of the spin boson model31 with a tailored spectral function and, with the help of the additional drive tones, explore it in the ultra-strong coupling regime32,33.

Methods

Dispersive measurement of the qubit population

As described in the main text, we determine the qubit state via the dispersive shift of the readout resonator. Since our measurement setup lacks a quantum-limited amplifier, each data point is pre-averaged 500 times on the data acquisition card. This is repeated 25 times to calculate the standard deviation of the mean. Additionally, we had to calibrate the position of the resonator for ground and excited state. Especially, time dependent fluctuations of the resonator frequency would otherwise prove detrimental. Therefore, the measurement sequences for each time trace include two additional points: For the first, we measure the dispersive shift after a π-pulse was applied to the qubit, which gives a reference point for the excited state. Second, the qubit frequency is tuned along the trajectory through the resonator ensemble and its state is measured after tuning it back to ωi. Since no excitation pulse is applied this gives a reference for the ground state. In the IQ-plane, we project all other data points in the sequence onto the connection line between the two reference measurements. The (effective) qubit population is then given by

$${P}_{{{{\rm{q}}}}}=\frac{{x}_{i}-{x}_{{{{\rm{g}}}}}}{{x}_{{{{\rm{e}}}}}-{x}_{{{{\rm{g}}}}}},$$
(3)

where xi is the position of point i along the line, and xg/e denotes the position of ground/excited state. The standard deviation is calculated from Gaussian error propagation.

Offset calibration

We calibrate the offset of our time traces in the measurement by comparison with the numerical simulations. Here, we minimize the mean squared error between each data point and its corresponding point in the numerical simulation, as a function of a time and frequency offset to the qubit population. We find the lowest deviation for a shift of 5.2 ns and 2.4 MHz of the quantum simulation with respect to the numerical results.